Пифагор теоремасының дәлелдерін қарастыру

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

Әбіш Кекілбайұлы атындағы №72 ЖББО ІТ мектеп-лицейі

Бағыты: Экономикалық және әлеуметтік

үрдістерді математикалық модельдеу

Секция: Қолданбалы математика

Зерттеу жоба тақырыбы:

ПИФАГОР ҮШТІГІ, ПИФАГОР ТЕРЕМАСЫНЫҢ ТЕХНИКАДАҒЫ ҚОЛДАНЫСЫ

Орындаған: Әбіш Кекілбайұлы

атындағы №72 ЖББО ІТ мектеп-

лицейінің 9Ә класс оқушы

Мәулетшәріп Әсем

Жетекшісі: Әбіш Кекілбайұлы атындағы

№72 ЖББО ІТ мектеп-лицейінің

математика пәнінің мұғалімі Әлімбаева

Сарқыт Бахитқызы

Ақтөбе-2022ж.

МАЗМҰНЫ

КІРІСПЕ . . . 3

1 ТЕОРИЯЛЫҚ БӨЛІМ

1. 1 Пифагор туралы . . . 5

1. 2. Пифагор теоремасы . . . 6

1. 3 Пифагор үштігін есептеу әдісі . . . 8

2 ПРАКТИКАЛЫҚ БӨЛІМ

ПИФАГОР ТЕОРЕМАСЫН ПРАКТИКАЛЫҚ ҚОЛДАНЫСЫ . . . 10

2. 1. Пифагор теоремасы бойынша және Пифагор үштігі арқылы шығаруға арналған практикалық тапсырмалар . . . 10

2. 2. Пифагор теоремасының қолданысы және пайдасы . . . 16

ҚОРЫТЫНДЫ . . . 19

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 21

КІРІСПЕ

«Пифагор үштігі, Пифагор теоремасы оның техникадағы қолданысы» атты математика пәні бойынша оқушылардың зерттеу жұмысында автор оқу-әдістемелік әдебиеттерге талдау жасайды және Пифагор туралы қызықты мәліметтерді табады. Сондай-ақ, жобада Пифагор теоремасының дұрыс тұжырымы ұсынылған, теореманың дәлелі келтірілген және Пифагордың әйгілі философиялық тұжырымдары ұсынылған. Аталған тақырып бойынша шығармашылық және зерттеу жобасында оқушылар Пифагор үштігін есептеу әдістері және оның программалық коды жазылған. Пифагор теоремасының ұқсас үшбұрыштар арқылы дәлелі берілді, сонымен қатар Пифагор теоремасының құрылыста, ұялы байланыста, астрономияда және әдебиетте қолданылуы қарастырылды. Оқушы Пифагор теоремасын адамның күнделікті өмірінде қолданудың өзектілігі туралы айтады. Геометрия сабақтарында біз ежелгі уақыттан бері белгілі тікбұрышты үшбұрыш үшін геометрияның маңызды теоремаларының бірі - Пифагор теоремасымен таныстық: тікбұрышты үшбұрышта гипотенузаның квадраты катеттердің квадраттарының қосындысына тең. Біз осы теореманың тарихымен қысқаша танысып, оның бір дәлелін қарастырдық, сонымен қатар дәлелдеудің басқа тәсілдері бар екенін білдік. Пифагордың есімі оның теоремасымен байланысты болмайтын адамды табу қиын. Барлығы дерлік «Пифагор теоремасының» естеліктерін сақтап қалды - гипотенузадағы шаршы, катеттері екі шаршыға тең. Пифагор теоремасының танымал болуының себебі айқын: қарапайымдылық, сұлулық және кең маңыздылығы. Алайда, Пифагор теоремасы қарапайым, бірақ айқын емес. Екі қарама-қайшылықты принциптердің бұл үйлесімі оған ерекше тартымды күш береді, оны керемет етеді. Сонымен қатар, Пифагор теоремасы үлкен мәнге ие: ол геометрияда әр қадам сайын қолданылады және осы теореманың 500-ге жуық түрлі дәлелі бар (геометриялық, алгебралық, механикалық және т. б. ) оның нақты іске асырылуының үлкен санын көрсетеді. Пифагор теоремасын біле отырып, сіз оның жаңа қосымшалары мен дәлелдеу әдістерін таба аласыз. Бір жағынан, Пифагор теоремасы мектеп геометрия курсында зерттеліп, дәлелденеді, ал екінші жағынан, мектеп материалы оның әртүрлі, соның ішінде адам қызметінің қазіргі салаларында практикалық маңыздылығын көрсету үшін жеткіліксіз.

Жұмыстың мақсаты: Пифагор теоремасының және Пифагор үштігінің практикалық қолданылуын зерттеу.

Жұмыстың -міндеттері:

1. Пифагордың өмірбаянын зерттеу.

2. Пифагор теоремасының пайда болуы мен даму тарихын зерттеу.

3. Пифагор теоремасының дәлелдерін қарастыру.

4. Пифагор үштігін есептеу әдістерін талдау.

5. Пифагор теоремасын, үштігін қолдана отырып шешілетін қызықты есептер мен тапсырмалар.

Зерттеудің негізгі әдістері: деректерді зерттеу, жүйелеу және өңдеу әдісі.

Гипотеза: егер Пифагор теоремасы және үштігі бүгінде соншалықты танымал болса, онда оны әртүрлі, соның ішінде адам қызметінің қазіргі салаларында қолдануға мүмкіндік беретін негіздер бар.

Зерттеу нысаны: Пифагор теоремасын және үштігін қазіргі адам қызметінде практикалық қолдану.

Зерттеу пәні: Пифагор теоремасы, Пифагор үштігі (геометиря)

1 ТЕОРИЯЛЫҚ БӨЛІМ

ПИФАГОР ТУРАЛЫ

Пифагор туралы: «Олимпиадаға қатысып қана қоймай, барлық қарсыластарын жеңді»- деп басталады, әрине бұл аңыз. Бұл жас Пифагор болды - әйгілі математик. Оның бүкіл өмірі-аңыз, дәлірек айтқанда көптеген аңыздардың қабаттасуы. Ол Кіші Азияның жағалауындағы Самос аралында дүниеге келген. Тек 5 шақырым су беті бұл аралды үлкен жерден бөліп алды. Өте жас Пифагор Отаның тастап кетті. Ол Египеттің жолдарымен жүріп өтті, Вавилонда 12 жыл тұрды, онда ол астрономия мен астрологияның құпияларын ашқан діни қызметкерлердің сөздерін тыңдады, содан кейін бірнеше жыл - Италияда. Ересек жаста Пифагор Сицилияға қоныс аударады және сол жерде Кротонда Пифагор деп аталатын таңғажайып мектеп жасайды. Олар еңбекқор және аскетикалық болды - Пифагор және оның шәкірттері. Міне, пифагорлықтардың өсиеттері:

Тек кейінірек сізді ренжітпейтін және өкінуге мәжбүр етпейтін нәрсені;
Денеңіздің денсаулығын ескеріңіз.
Қарапайым және сән-салтанатсыз өмір сүруге үйреніңіз.
Ұйықтамас бұрын, бір күндегі әрекеттеріңізді талдаңыз.

Пифагорға, оның оқушыларына қандай ғылыми идеялар тиесілі екенін айту қиын. Бірақ олар Пифагор өзінің әйгілі теоремасын дәлелдеп, құдайларға алғыс айтып, оларға 100 бұқа құрбандыққа шалды дейді. Пифагор өзінің ілімдерін жазған жоқ. Бұл тек Аристотель мен Платонның қайталануларында белгілі. Грек ғалымы Гераклит Пифагор барлық замандастарына қарағанда жақсы деп мәлімдеді, бірақ оны сиқырға бейімділігі үшін айыптады. Пифагорлықтарға арналған сандар сиқырлы мазмұнға толы болды, олар сандар үйлесіміне табынды. Пифагор тек математик қана емес, философ болды. Ол көптеген үлкен болжамдарға ие. Сондықтан адамдар оны екі жарым мың жылдан бері есіне алады, ал әйгілі Олимпиада чемпиондарының ішінде Пифагор ең танымал - ол қарсыласын ғана емес, уақытты да жеңу бақытына ие болды.

Пифагор (б. з. д. 580-500 ж. ж. ) Самос аралында, Ионияның гүлденген аралдарының бірі, бай зергердің отбасында дүниеге келді. Ол өте әдемі болды және бала кезінен ақыл мен әділеттілікпен ерекшеленді. Жас кезінен бастап Пифагор Мәңгілік табиғаттың құпияларына енуге, болмыстың мағынасын түсінуге тырысты. Грецияның ғибадатханаларында алған білімі оны толғандыратын барлық сұрақтарға жауап бермеді және ол Мысырға даналық іздеуге кетті. 22 жыл бойы ол Мемфис храмдарында оқыды және жоғары дәрежеге ие болды. Мұнда ол математиканы, сандар ғылымын немесе Дүниежүзілік қағидаларды терең зерттеді, одан кейін ол өз жүйесінің орталығын жасады. Пифагор математик болумен қатар, әдебиет пен философиямен де байланысты болды.

Пифагорды өз заманының ұлы ойшылдарына жатқызуға болады. Пифагордың маңызды жетістіктерінің бірі-оның есімімен аталатын теореманың дәлелі. Оны дәлелдеудің 500-ге жуық тәсілі бар және бұл математикалық Теоремалардың көпшілігін дәлелдейтін Теоремалардың бірі.

ПИФАГОР ТЕОРЕМАСЫ

Пифагор теоремасы 100-ден астам жолмен дәлелденді. Біз теореманы дәлелдеудің үш жолымен таныстық. Міне, осы теореманың қарапайым геометриялық дәлелі: дұрыс үшбұрыштың гипотенузасына салынған квадраттың ауданы оның катеттеріне салынған квадраттардың аудандарының қосындысына тең.

а және b катеттері мен c гипотенузасы бар тікбұрышты үшбұрышты қарастырамыз (сур. 1) . Екі квадратты сызыңыз, олардың жақтары (A+b) - оң үшбұрыштың екі аяғының қосындысына тең. Содан кейін алынған квадраттарда біз құрылысты орындаймыз (сурет. 2, сурет. 3) .

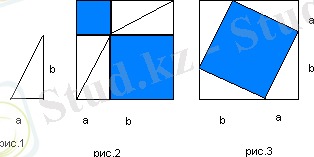
Безымянный

1-сурет. 2-сурет. 3-сурет.

Барлығы суретте көрсетілген. 2 және 3 фигуралар - тік бұрышты үшбұрыштың катеттері мен гипотенузасына тең жақтары бар квадраттар. Суретте көрсетілген квадраттардың аудандарының қосындысы анық. 2 (a ² + b ² ) суреттегі сызылған шаршының ауданына тең. 3сурет (с ² ), атап айтқанда: квадраттың ауданы (a+b) тең үшбұрыштардың төрт ауданын алып тастағанда.

Сонымен, Пифагор теоремасы дәлелденді.

Теореманың тағы екі дәлелі келтірілген.

Көпбұрыштардың аудандарының қасиеттерін қолдана отырып, гипотенуза мен оң үшбұрыштың катеттері арасындағы керемет қатынасты орнатамыз.

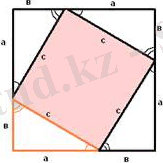
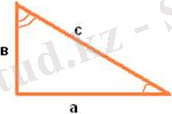
Сур. 4 Сур. 5

a және b катеттері мен с гипотенузасы бар тікбұрышты үшбұрышты қарастырамыз (сур. 4) . Дәлелдейік, бұл $c^{2} = \ a^{2}{+ \ b}^{2}.$

Дәлел:

Біз үшбұрышты a + b жағы көрсетілген шаршыға дейін жеткіземіз (сурет. 5) . Осы квадраттың s ауданы $(a + b) ^{2}$ . Екінші жағынан, бұл шаршы төрт тең тікбұрышты үшбұрыштардан тұрады, олардың әрқайсысының ауданы тең $\frac{1}{2}ab$ , және С жағы бар шаршы, сондықтан

S = $4 \bullet \frac{1}{2}ab + \ c^{2} = 2ab + \ c^{2}$ . Осылайша, $(a + b) ^{2} = 2ab + \ c^{2}$ , осыдан

$\ {\ c}^{2} = \ a^{2} + \ b^{2}$ . Теорема дәлелденді.

Пифагор теоремасының Перигалдың қызықты дәлелі.

Бұл дәлел негізделген квадраттарды кесу, катеттерге салынған (сур. 6) және алынған бөліктерді гипотенузаға салынған квадратқа салу. Оқулықтарда суретте көрсетілген ыдырау жиі кездеседі («пышақтары бар доңғалақ» деп аталады; бұл дәлел Перигалды тапты) . Үлкен катетке салынған шаршының ортасы арқылы біз гипотенузаға параллель және перпендикуляр сызықтар саламыз. Фигураның бөліктерінің сәйкестігі Сызбадан айқын көрінеді.

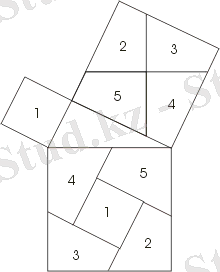
Сур. 6

Пифагор теоремасы (дәлелсіз) Вавилон мәтіндерінде кездеседі, Пифагордан 1200 жыл бұрын жазылған. Ол қытай мен Үндістанда танымал болды. Евклид өте қиын Пифагор теоремасының ең көне дәлелдерінің бірін енгізді. Біздің дәуірімізге дейінгі 200 жыл ішінде ұзындығы 3, 4, 5 бірліктері бар тікбұрышты үшбұрыш туралы, мысырлықтар оны сиқырлы деп санады.

ПИФАГОР ҮШТІГІН ЕСЕПТЕУ ӘДІСІ

Пифагор есебінің негізгі мақсаты келесі теңдеуді шешу болып табылды: x ² + y ² = z ² . Бұл теңдеуді шешудің мағынасы осы қатынастар орындалатындай үшбұрыштың бар болуы және оны шешу еді. Осы теңдеуді қанағаттандыратын ( х, у, z) натурал сандарды Пифагор үштігі деп атады. Мысалы, барлығымыз білетіндей 3, 4, 5 сандары. Сонымен қатар бұл сандардың қосындысы 12-ге, ал осы үшбұрыштың ауданы 6-ға тең болды, сондықтан бұл санды сол кездегі аңыздар бойынша бақытты сан деп есептеген. Атақты Фараон Снофру пирамидасын салуға осындай олшемдегі үшбұрыштар қажет болған: 20, 21, 29 және 18, 24, 30 мысырлық білектер өлшемімен. Тағы бір мәліметтерде ескі вавилондықтандан 15 пифагорлық сандар бейнеленген қыш тақтайшасы табылған болатын. Ол тақтайшада тіпті (12709, 13500 и 18541) -үштігі де кездеседі.

Пифагор үштігін табу әдісі

Сонымен x ² + y ² = z ² теңдеуі қалай шешіледі ?

Бірінші әдіс: Натурал сандардың квадраттарын қатарынан жазып шығамыз, әр квадраттың астына сәйкесінше сол сандардың айырмасын жазамыз:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, . . .

3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, . . .

Сонда екінші қатарда натурал сандардың квадраттары кездеседі: мысалы бірінші кездесетін сан- 9, ал жоғарғы қатарда 16 және 25, яғни бізге таны Пифагор үштігі (3, 4, 5) . Келесі квадрат 25, ал оның жоғарғы жағында 144 пен 169, яғни 5, 12, 13. Міне, осындай заңдылықпен Ежелгі Мысарда осылай Пифагор үштіктерін таба бастаған. Әрине бұл әдіс өте ауқымды және тиімсіз. Сондықтан келесі әдісті ұсынамын.

Екінші әдіс: Бұл формула ежелден таныс: (x, y, z, ) -Пифагор үштігі болсын, х-тақ сан. онда $y = \frac{x^{2} - 1}{2}, \ z = \frac{x^{2} + 1}{2}$

Үшінші әдіс: Пифагор теңдеуін келесі түрде жазайық:

$x^{2} = z^{2} - y^{2}\ \ немесе\ x^{2} = (z - y) (z + y) \ \ \ \ \ \ \$

Яғни ізделінді сан екі санның көбейтіндісіне тең болуы керек. Біз келесідей белгілеулер енгізейік: z + y = 2m ² , z - y = 2n ² . Осы теңдеуді шеші арқылы келесі жауапты аламыз: z=m ² +n ² , y= m ² -n ² . Осы айнымалыларды бастапқы теңдеуге қойсақ, келесі мәндерді аламыз: x=2mn, m>nжәне олар кез-келген натурал сандар. Келтірілген формулаларды қолдана отырып x ² + y ² = z ² теңдеуін натурал сандар жиынында жеңіл шешуге болады ^. Мысалы: m = 9, n = 7, m>n.

x = 2mn, x = 2* 9 *7 = 126;

y = m^2 - n^2, y = 81 - 49 = 32;

z = m^2 + n^2, z = 81 + 49 = 130.

Яғни, 126 + 32 = 130, 15876 + 1024 = 16900

Жауабы: 126, 32, 130.

Премитивті пифагор үштігі және оның қасиеті

Ортақ бөлгіші жоқ пифагор үштігін премитивті немесе қарапайым деп атайды. Мысалы: (3, 4, 5), (5, 12, 13), (8, 15, 17), (9, 40, 41) тсс. Егер (х, у, z) -пифагор үштігі премитивті болса, онда (nx, ny, nz) -премитивті болады. Пифагор осындай қарапайым үштіктерді табудың келесі формуласын тапқан:

х = 2n + 1, y = 2n(n + 1), z = 2n + 2n + 1, мұндағы n- натурал сан.

Премитивті пифагор үштігінің келесі қасиеттері белгілі:

1 қасиет. Қарапайым үштікке енетін сандар өзара жай сандар.

Салдар : Карапайым пифагор үштігінде бір сан жұп бола алады.

2қасиет. (x, y, z) -қарапайым пифагор үштігінде x және y бір мезетте тақ бола алмайды.

3 қасиет . Қарапайым пифагор үштігінің біреуі міндетті түрде 3- ке еселі болады.

4 қасиет . Қарапайым пифагор үштігінің біреуі міндетті түрде 4- ке еселі болады.

5қасиет. Қарапайым пифагор үштігінің біреуі міндетті түрде 5- ке еселі болады.

Болашақта қарапайым Пифагор теңдеуі x ² + y ² = z ² келесі жаңалық болған келесі теңдеуді шешуге әкеліп соқты: x ⁿ + y ⁿ = z ⁿ .

2. ПИФАГОР ТЕОРЕМАСЫН ПРАКТИКАЛЫҚ ҚОЛДАНЫСЫ

2. 1. Пифагор теоремасы бойынша және Пифагор үштігі арқылы шығаруға арналған практикалық тапсырмалар

Арқан арқылы есептеу.

Жергілікті жерде дұрыс бұрыштарды салу кезіндегі Пифагор теоремасы қолданылады. «Арқанды тарту» арқылы дұрыс бұрыштарды салу әдісін көбейту өте оңай. Арқанды алып, оны бөлетін белгілерді жасаңыз. 12 тең бөлікке бөлу. Біз оның ұштарын байлап, 3, 4 және 5-ке тең жақтары бар үшбұрыш түріндегі тіректерді пайдаланып, арқанды жерге созамыз. Содан кейін ұзындығы 3 және 4 метр болатын Жақтардың арасында дұрыс бұрыш жасалады (сурет. 7) .

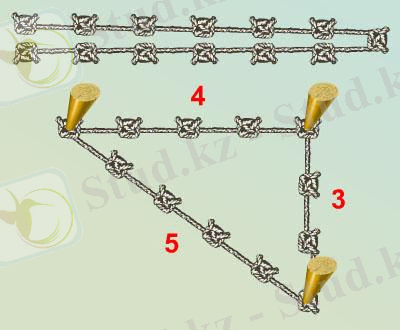
Сур. 7

Готикалық және романескалық стильде терезе салу

Готикалық және романескалық стильдегі ғимараттарда терезелердің жоғарғы бөліктері ою-өрнек рөлін атқарып қана қоймай, сонымен қатар терезелердің беріктігіне ықпал ететін тас қабырғалармен бөлінген (№2 қосымша) . Суретте (сурет. 8) готикалық стильдегі осындай терезенің қарапайым мысалы келтірілген. Оны құру әдісі өте қарапайым: Сызбадан радиусы сыртқы доғалар үшін терезе еніне (b) және ішкі доғалар үшін жарты енге (b/2) тең алты шеңбер доғасының орталықтарын табу оңай. Төрт доғаға тиетін толық шеңбер саламыз. Ол екі концентрлік шеңбердің арасында орналасқандықтан, оның диаметрі осы шеңберлер арасындағы қашықтыққа тең, яғни b / 2, сондықтан радиусы b/4. Содан кейін оның орталығының орны айқын болады.

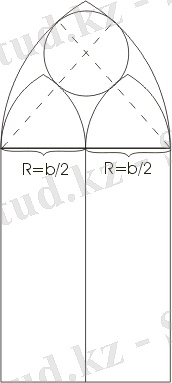
$C:\Users\User\Documents\Из интернета\применение.files\use04.gif$

Сур. 8

Қарастырылған мысалда радиустар еш қиындықсыз болды. Басқа ұқсас мысалдарда есептеу қажет болуы мүмкін. Пифагор теоремасы осындай мәселелерде қалай қолданылатынын көрсетеміз.

Романескалық архитектурада жиі ұсынылған мотив бар (№3 қосымша) . Суретте (сурет. 9) Егер b әлі де терезенің енін көрсетсе, онда жартылай шеңбердің радиусы R = b / 2 және r = b / 4 болады. Ішкі шеңбердің p радиусын суретте көрсетілген дұрыс үшбұрыштан есептеуге болады. пунктиром. Шеңбердің жанасу нүктесінен өтетін осы үшбұрыштың гипотенузасы b / 4 + p, бір аяғы b / 4, ал екіншісі

b / 2-p. Пифагор теоремасы бойынша бізде: (b/4+p) ² =( b/4) ² +( b/2-p) ² немесе b ² /16+ bp/2+p ² =b ² /16+b ² /4-bp+p ² , осыдан bp/2=b ² /4 - bp. B - ге бөліп, ұқсас мүшелерді алып, біз аламыз: (3/2) p=b/4, p=b/6.

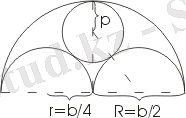
$C:\Users\User\Documents\Из интернета\применение.files\use05.gif$

Сур. 9

Шатырдың құрылысы

Үйлер мен коттедждерді салу кезінде көбінесе габельді шатырға арналған рафтерлердің ұзындығы туралы сұрақ туындайды (4-қосымша) . Мысалы: ғимараттың ені 6 м, шатырдың биіктігі 2 м (сурет. 10) . Рафтерлердің ұзындығы қандай болуы керек?

Шешім: тікбұрышты үшбұрышта бір аяқтың ұзындығы-a = 2 м (ғимараттың ені), екінші аяғының ұзындығы-b = 6: 2 = 3 (м) . Пифагор теоремасына сәйкес біз гипотенузаны табамыз (рафтерлердің ұзындығы) : c = $\sqrt{2^{2} + 3^{2}}$ $\approx 3, 6(м) .$

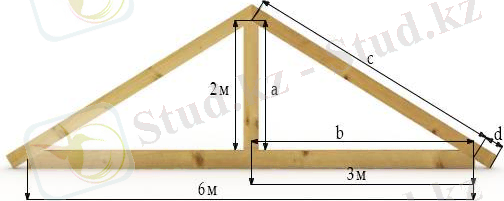
Сурет- 10

Осы тапсырманы негізге ала отырып, біз габельді шатырды зерттеп, ол үшін Пифагор теоремасы орындалғанын тексеруді шештік. Шатырды өлшегеннен кейін біз келесі нәтижелерге қол жеткіздік: сәуленің ұзындығы - 12, 2 м, биіктігі - 3 м, рафтерлердің ұзындығы - 6, 8 м.

Екіжақты шатыр (двускатная крыша) қимасында - тең бұрышты үшбұрыш, онда ұзындығы тіреуіштерді Пифагор теоремасы бойынша есептейміз: $\sqrt{{6, 1}^{2} + 3^{2}}\$ ≈ 6, 8 (м) . Өлшеу қателігін ескере отырып, шатыр құрылысында жұмысшылар белгілі теореманы қолданды деген қорытындыға келеміз.

Пифагор теоремасына арналған тапсырмалар:

1-тапсырма.

Биіктігі 9 м тіректен үйге дейін биіктікте бекітілген сым тартылады

Жерден 3 м (суретті қараңыз) . Үйден бағанға дейінгі қашықтық-8 м. сымның ұзындығын есептеңіз.

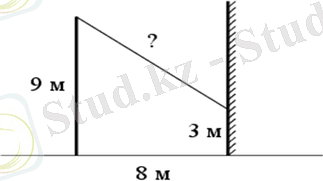
Шешуі: пифагор 5

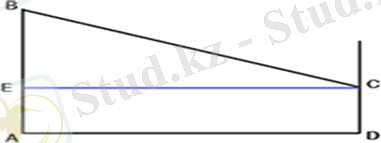пифагор 6 Біз сызбалы қ түрде сурет саламыз. AD-ге параллель СЕ кесіндісін сызыңыз. ABCD-тіктөртбұрыш, өйткені барлық бұрыштар түзу. Демек, CE=AD.

Пифагор теоремасы бойынша

BC ² =CE ² +EB ² , BC ² =82 + (9-3) ² , BC ² =64+36, BC ² =100, BC=10.

Жауап:10.

2-тапсырма.

Бүктелген түрдегі баспалдақтың ұзындығы-1, 85 м, ал ашылған кездегі биіктігі-1, 48 М. ашылған түрдегі баспалдақтың негіздері арасындағы қашықтықты (метрмен) табыңыз.

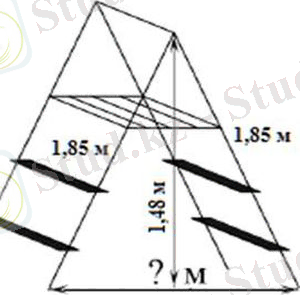
пифагор 7

Шешуі

Бұл есепті Пифагор теоремасы арқылы жеңіл табуға болады, жауап: 2, 22.

3-тапсырма.

Қыз үйден батысқа қарай 880 м бағытта өтті, содан кейін солтүстікке бұрылып, 900 м өтті, содан кейін ол шығысқа бұрылып, тағы 400 м өтті. қыз үйден қандай қашықтықта (метр) болды?

Шешім:

Шығыс пен Батыс − қарама-қарсы бағыттар, сондықтан қыз батысқа қарай 880-400 = 480 м өтті. Оң жақ үшбұрыштың гипотенузасы болсын. Пифагор теоремасына сәйкес гипотенузаны жеңіл табамыз, жауап: 1020.

Ұялы байланыс

4 -тапсырма.

Беріліс R=200 км радиуста қабылдануы үшін ұялы байланыс операторының антеннасы қандай биіктікке ие болуы керек? (жердің радиусы-6380 км. )

Шешім:

Айталық, AB=x, BC=R=200 км, OC=r=6380 км.

OB=OA+AB

OB= r + x.

Пифагор теоремасын қолдана отырып, біз 23 км аламыз

Жауабы: 23 км.

Астрономия

5-тапсырма. Бұл суретте A және B нүктелері және жарық сәулесінің А-дан В-қа дейінгі жолы көрсетілген. Сәуленің жолы анық болу үшін иілген көрсеткімен көрсетілген, іс жүзінде жарық сәулесі түзу. Сәуле қандай жолмен өтеді? Жарық бірдей жолмен жүретіндіктен, бірден сұраңыз: нүктелер арасындағы қашықтық қандай?

Шешуі:

Бұл суретте жарық сәулесінің жолы тек басқа тұрғыдан, мысалы, ғарыш кемесінен көрінеді. Кеме солға қарай жылжиды делік. Содан кейін жарық сәулесі қозғалатын екі нүкте сол жылдамдықпен оңға қарай жылжиды. Сонымен қатар, Сәуле өз жолымен өтіп бара жатқанда, бастапқы нүкте а жылжып, сәуле жаңа c нүктесіне оралады.

Пифагор үштігіне арналған тапсырмалар

Келесі есептерді қарастырайық:

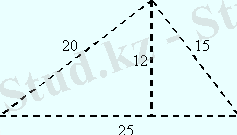
№1 Шырпылардан биіктігі 12 -ге тең болатын әртүрлі қабырғалы үшбұрыш тұрғызу.

Шешуі: Бұл есепті қарапайым Пифагор үштігімен жеңіл шешуге болады, яғни биіктікке тірелетін екі үшбұрыш пифагор үштігін қанағаттандыруы тиіс. Бір катеті тақ болса, екіншісі жұп болған. Сонымен келесі сандар шешім болып табылады: (3, 4, 5) және (4, 3, 5) үштіктерін алып, 3-ке, 4-ке сәйкесінше көбейтсек (12, 16, 20) және (12, 9, 15) болады. Яғни жауабы 20, 15 және 16 + 9 = 25 болғаны.

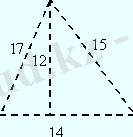
№2. Қабырғалары: 5, 12, 13 болатын үшбұрыштың үлкен қабырғасына медиана жүргізілген. Осы медина бөліп тастаған үшбұрыштарға іштей сызылған шеңберлердің центрлеріннің ара қашықтығын табыңыз

Шешуі: (5, 12, 13) - пифагор үштігі, сондықтан ол үшбұрыш тік, сондықтан тік бұрышты үшбұрыштың медианасының қасиетін пайдалана отырып, екі теңбүйінһрлі үшбұрыштың пайда болғанын көреміз. Есеп осы ереже арқылы тез шешімін табады.

№3 Табыңыз: cos , tg и ctg , егер sin = 24/25, - екінші ширекке тиісті.

Ш ешуі: Бұл есепті (7, 24, 25) - пифагор үштігімен жеңіл шешуге болады. Берілген мәндерді ескере отырып, келесі шешімді аламыз:

cos

http://festival.1september.ru/articles/618788/img14.gif

= - 7/25, tg

= - 24/7, ctg

= - 7/24.

№4. Үйдің сыртың әдемілеу үшін тік бұрышты үшбұрыш пішінді, катеткі 10-ға тең әйнек мозайкадан құру керек еді. Онда оның қалған қабырғалары нешеге теі болуы керек?

Шешуі: Берілген катет жұп сан, яғни х = 10 = 2mn, мұндағы m>n және өзара жай сандар. . Бұл тек жалғыш комбинациямен орындалады: m, n - бұл 5 және 1. Сонымен 2*5*1=10. у=m ² -n ² =24, z=m ² +n ² =26. Жауап: 10см, 24 см және 26 см.

Сонымен, қорыта келгенде, Пифагор үштігі күрделі есептерді тез әрі дұрыс шығаруға көмектеседі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.