Ақырлы және саналымды бірыңғай Марков құбылыстары: қасиеттері, класстарға бөлу, Колмогоров теңдеулері және стохастикалық жүйелерге қолданбалары


Мазмұн
Кіріспе
1. Ақырлы және саналымды жағдайдағы Марков құбылысы
1. 1. Марковтік қасиет және ауыспалы ықтималдылық
1. 1. 1. Марков құбылысындағы уақыт моменті
1. 1. 2. Бірыңғай Марков құбылысы
1. 1. 3. Колмогоров теңдеуі
1. 1. 4. Минимал ауыспалы ықтималдылық
1. 2. Бірыңғай Марков тізбегін класстарға бөлу
1. 2. 1. Бірыңғай Марков тізбегінің нөлдік және оң жағдайы, қайтуының орташа уақыты, тұйық жиын
Қорытынды
Пайдалынылған әдебиеттер
Кіріспе
Марков құбылысының кластарға бөлінуі кездейсоқ құбылыстардың дербес түрі болып табылады. Кездейсоқ құбылыстардың ішінде Марков құбылысы маңызды орын алады. Бұл құбылыстың екі түрін айтар болсақ: біріншіден математика саласында Марков құбылысы жақсы талданған және физикалық есептерді шешуге, екіншіден Марков құбылысының көмегімен қатар тәртібінің физикалық жүйесін құруға мүмкіндік береді.
Марков құбылысының теориялық базасында шешуге болатын есептерге мысалдар келтірейік:
- Динамикалық жағдайда кездейсоқ құбылысты түрлендіргенде сызықты және сызықсыз болатыны бізге белгілі, ереже бойынша статистика характеристикасының шығатын құбылысын анықтайтын әдіс жоқ. Осыдан қорытындылайтынымыз нормаль құбылыс үшін сызықты түрлендіру құрамыз. Кореляциялық теория әдісінің қасиетін сақтай отырып нормалді және толық өлшемді қолданамыз. Ықтималдылық тығыздығын жуықтау әдісінің моментін есептеу арқылы қалпына келтіреміз. Бірақ жүйеге әсер ететін құбылыс марковтік болып табылады, статитика характеристикасының шығатын құбылысына есептеу әдістерін қолданамыз.
- Шектелген аймақтағы фазалық кеңістіктегі жүйенің қозғалысы нүкте қозғалысынан пайда болады. Мұндай есептердің түрі автоматты басқару жүйесінде шығарылады. Қазіргі уақытта кескінді нүктенің қозғалысын практикада көптеп ұсынады. Физиканың маңызды есептерін аналитикалық жолмен Марков құбылысында ғана шешеді.
- Қазіргі уақытта басты даму барысында радиотехника және автоматтандыру жатады. Марков құбылысы үшін бұл бағыттан нақты нәтиже алуға болады.
Қолданбалы есептерді шешкенде математикалық әдістерінің мысалдарында мақсаты көрсетілмейді. Ереже бойынша математикалық амалдарға есептер қарастырғанда белгілі арсеналды қолдана білу керек. Аналитикалық әдістердің көбі Марков құбылысында шығарып қарастырылған.
Енді Марков құбылысының теория апаратындағы есептерді шығару кезінде қолданылатын екі дәлелдеуді корсетейік
- Тәжірибелік жағдайларда жолақты кедергі немесе флуктуациялық дыбыстарды салыстырмалы инерциялық жүйенің ақырлы қатарына әсер етуін жиі қарастыруға болады. Осындай эквивалентті шулдардың аналитикалық шектік жүйеге әсер етуі Марков жүйесінде қарауға мүмкіндік береді.
- Рационал бөлшек функциясының нақты дәрежелі жиілігі түріндегі энергетикалық спектордың кездейсоқ құбылысы үшін Марков құбылысын жуықтауға болады.
Тақырыптың өзектілігі: есептелетін сандар жағдайындағы Марков құбылысын сызықсыз схоластикалық диференциялдық теңдеулерді шешуде автоматты фазалық жиілігінің орташа уақыты және кедергі қосылатын дисперсия уақытын есептеп, кесте құрып, графигін салу.
Жұмыстың мақсаты: сызықсыз схолостикалық диференциалдық теңдеудің алғашқы қатарындағы [22] алынған теңдеудің амплитудасы мен адитивті n(t) шулындағы гармониялық жүйеге кіретін белгінің ықпалымен синусоида сипатындағы алғашқы ретті автоматты құрылған фазалық жиілігінің орташа уақытын және кедергі қосылатын дисперсия уақытын есептеу, есетелетін сандар жағдайындағы Марков құбылысының тепе- теңдік орнықты күйін анықтау.
Ғылыми жаңашылдығы: ықтималдықтар теориясының марковтік тізбек теориясына негізделген іргелі ұғымдарын, құбылыстың бірыңғайлығын класстарға бөлу, бірыңғай Марков тізбегіндегі эргодикалық қасиеттерін, Колмогорвтің кездейсоқ үлестірудегі құбылыстардытұрғызу теориясы, шектік теоремаларды дәлелдеудің сипаттамалық функциялар әдісін, үлестірімдердің белгісіз параметрлерін бағалау теориясын, өтпелі графа және оның марков тізбегімен байланысы, кездейсоқ құбылыстың теориясын, Марков құбылыстарының негіздерін терең зерттеп, жаңаша амалдар қолдану арқылы тұжырымдар қорытып шығарылды, Марков тізбегіндегі қолданылатын әдіс тәсілдерін, қасиеттерін, мысалдарын есептеу.
Жұмыстың нәтижесі: ықтималдықтар теориясы, математикалық статистика және кездейсоқ құбылыстар теориясының негіздеріне қатысты Марков тізбегінің түрлері қарастырылып есептері талқыланды.
Жұмыстың құрылымы: үш бөлімнен тұрады: бірінші бөлімде Марковтік құбылыстың қасиеттері мен ауыспалы ықтималдылығы және оларды класстарға бөлу, эргодикалық қасиеті туралы мәліметтер қарастырылған. Екінші бөлімде тақырыпқа тікелей байланысты «Есептелетін сандар жағдайындағы Марков тізбегінің топологиялық қысым үшін варияциялық принципінің анықтамасы мен нәтижелері қарастырылып мысалдар келтірген. Колмогоровтың кездейсоқ үлестірудегі құбылыстарды құру теоремасы. Үшінші бөлімде осы екі бөлімде айтылған анықтамалар мен теоремаларды тұжырымдай отырып «Біріңғай Марков құбылысының шектелген жетістігін» есептеп, талдау жасалды. Осы жасаған есептеулерге анықтамалар мен теоремалар енгіздім. Қорытынды, пайдаланылған әдебиеттер және қосымшалардан тұрады.
Зерттеу әдістемесі:
сызықсыз схоластикалық дифференциялдық теңдеудің алғашқы қатарындағы
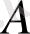 амплитудасы мен адитивті
амплитудасы мен адитивті
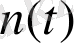 дыбысындағы гармониялық жүйеге кіретін белгінің ықпалымен синусоида сипаттамасындағы алғашқы ретті автоматты құрылған фазалық жиілігі орташа уақытын және кедергі қосылатын дисперсия уақытын есептеу, бірыңғай Марков құбылысының шектелген жетістігіндегі автоматты тұрғызылған жиілігін
дыбысындағы гармониялық жүйеге кіретін белгінің ықпалымен синусоида сипаттамасындағы алғашқы ретті автоматты құрылған фазалық жиілігі орташа уақытын және кедергі қосылатын дисперсия уақытын есептеу, бірыңғай Марков құбылысының шектелген жетістігіндегі автоматты тұрғызылған жиілігін
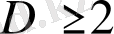 болғандағы
болғандағы
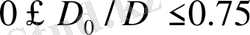 орташа уақытқа тәуелді мәніне сәйкес графигін саламыз.
орташа уақытқа тәуелді мәніне сәйкес графигін саламыз.
1. Ақырлы және саналымды жағдайындағы Марков құбылысы
1. 1 Марков қасиеті және ауыспалы ықтималдылық
Марков қасиеті.
Марков қасиетінің ауыспалы ықтималдылығын мынадай қарапайым мысалмен қарастырсақ болады. «Тыныш жүрсең - ұзақ жүресің» деген ойын бар. Бұл ойында ойнап отырған фишка ақырғы шегіне 1 . . . n жету керек. Ойнайтын допты бір бөлімнен екінші бөлімге лақтырғанда нәтижесі анықталады. Егер сол қадамда фишка
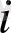 бөлімінде болса, онда ойнайтын доп түсірілген ұпайына байланысты ойынның шарты бойынша келесі қадамда ауыспалы болады.
бөлімінде болса, онда ойнайтын доп түсірілген ұпайына байланысты ойынның шарты бойынша келесі қадамда ауыспалы болады.
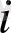 -дің кез келген бөлімінде
-дің кез келген бөлімінде
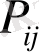 ауыспалы ықтималдылық
ауыспалы ықтималдылық
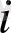 бөліміне тастамас бұрын тәуелсіз
бөліміне тастамас бұрын тәуелсіз
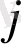 бөліміне ауысады.
бөліміне ауысады.

Айтылған қасиеттерді Марковтің кездейсоқ процессі деп аталады.
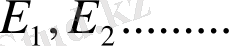 фазалық жағдайында жататын жүйені қарастыралық, параметріне қатысты жүйенің жағдайы өзгеріп отыратын қатысты оқиғаға тәуелсіз жүйеге ауысамыз.
фазалық жағдайында жататын жүйені қарастыралық, параметріне қатысты жүйенің жағдайы өзгеріп отыратын қатысты оқиғаға тәуелсіз жүйеге ауысамыз.
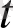 белгілеуін уақыт параметрі деп алсақ, жүріп өткен жол немесе нақты сан.
белгілеуін уақыт параметрі деп алсақ, жүріп өткен жол немесе нақты сан.
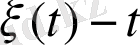 уақыт мезетінде жүйенің жайы болса мына заңдылық шығады:
уақыт мезетінде жүйенің жайы болса мына заңдылық шығады:
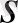 жүйесіндегі уақыт моменті фазалық жағдайында жатса, онда
жүйесіндегі уақыт моменті фазалық жағдайында жатса, онда
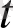 жүйесіндегі уақыт моменті
жүйесіндегі уақыт моменті
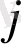 фазалық жағдайында жатады және
фазалық жағдайында жатады және
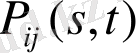 ықтималдылығы
ықтималдылығы
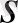 моментіндегі жүйенің қозғалысына тәуелді емес болады.
моментіндегі жүйенің қозғалысына тәуелді емес болады.
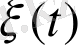 жүйесі Марков тізбегі деп аталады. Ықтималдылығы
жүйесі Марков тізбегі деп аталады. Ықтималдылығы
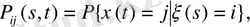
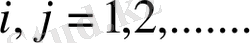 (1. 1. 1)
(1. 1. 1)
болса, Марков тізбегіндегі ауыспалы ықтималдылық деп аталады.
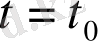 моментінің
моментінің
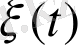 Марков тізбегіндегі жағдайын қарастырамыз. Егер
Марков тізбегіндегі жағдайын қарастырамыз. Егер
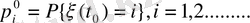 (1. 1. 2. )
(1. 1. 2. )
бастапқы ықтималдылықтың үлестірімі болса, онда
 (1. 1. 3)
(1. 1. 3)
кез келген
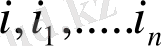 және
және
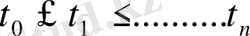 үшін орындалады
үшін орындалады
 .
.
- Марков құбылысындағы уақыт моменті.
 алдыңғыларға тәуелді емес кездейсоқ уақыт моменті болсын, сонда Марков тізбегі деп аталатын болады.
алдыңғыларға тәуелді емес кездейсоқ уақыт моменті болсын, сонда Марков тізбегі деп аталатын болады.
А кез келген оқиғасының пайда болуы
 моментінен кейінгі жүйенің шешіміне бағынады. Шарт бойынша моментіне дейінгі бұл оқиғаның ықтималдылығы шартты оқиғаға сәйкес келеді және
моментінен кейінгі жүйенің шешіміне бағынады. Шарт бойынша моментіне дейінгі бұл оқиғаның ықтималдылығы шартты оқиғаға сәйкес келеді және
 моментінде ғана
моментінде ғана
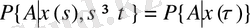 жүйесі орындалады.
жүйесі орындалады.
Кез келген
 және
және
 бөлігінде
бөлігінде
 (1. 1. 4)
(1. 1. 4)
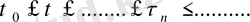 уақыт моментіндегі тізбегі
уақыт моментіндегі тізбегі
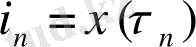 жағдайына сәйкес келетін моменті үшін қолданылады. Мысалы - ішжағдайдағы жүйеге бірінші қондыру моменті,
жағдайына сәйкес келетін моменті үшін қолданылады. Мысалы - ішжағдайдағы жүйеге бірінші қондыру моменті,
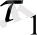 - бірінші
- бірінші
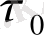 моментінен кейінгі жағдай,
моментінен кейінгі жағдай,
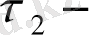 екінші моментінен кейінгі жағдай т. с. с. . Кез елген
екінші моментінен кейінгі жағдай т. с. с. . Кез елген
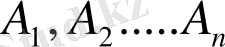 оқиғасы
оқиғасы
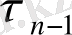
және
 дейінгі аралыққа сәйкес келетін толық жүйенің орналасуы өзара тәуелсіз болады
дейінгі аралыққа сәйкес келетін толық жүйенің орналасуы өзара тәуелсіз болады
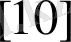 .
.
- Бірыңғай Марков құбылысы
Ауыспалы ықтималдылық
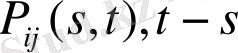 айырымына сәйкес келсе
айырымына сәйкес келсе
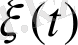 Марков тізбегі біріңғай деп аталады.
Марков тізбегі біріңғай деп аталады.
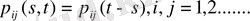 (1. 1. 5)
(1. 1. 5)
Мысал.
Кездейсоқ кезу. Барлық нүктелердің кездейсоқ кезуінің бөліктерін қарастырамыз. Әр қадамның р ықтималдылығының бөліктерінде 1 ығысу,
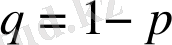 ықтималдылығында -1 ығысуы болады.
ықтималдылығында -1 ығысуы болады.
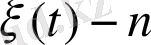 қадамынан кейінгі бөлшек болсын.
қадамынан кейінгі бөлшек болсын.
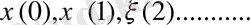 тізбегі Марков тізбегін құрайды: егер
тізбегі Марков тізбегін құрайды: егер
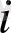 нүктесінде жатса, онда оның келесі орындалуы
нүктесінде жатса, онда оның келесі орындалуы
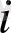 нүктесіндегі өткен шешімдерге тәуелді емес және
нүктесіндегі өткен шешімдерге тәуелді емес және
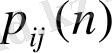 ықтималдылығы ауыстырым бөлігіндегі келесі
ықтималдылығы ауыстырым бөлігіндегі келесі
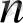 қадамы жағдайына сәйкес келеді.
қадамы жағдайына сәйкес келеді.
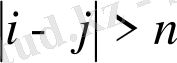 болғанда жағдайын жағдайына ауыстыру мүмкін емес және
болғанда жағдайын жағдайына ауыстыру мүмкін емес және
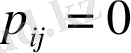 . Сонан соң қадамдағы бөлігі
. Сонан соң қадамдағы бөлігі
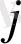 жағдайына өте алатыны белгілі,
жағдайына өте алатыны белгілі,
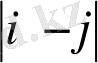 айырымы да осылай және
айырымы да осылай және
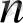 -де т. с. с. сандар үшін
-де т. с. с. сандар үшін
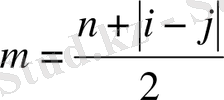
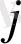 жағдайында
жағдайында
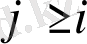 болғанда
болғанда
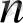 қадамы
қадамы
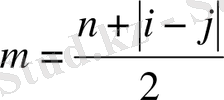 қадамына тең және бағыты оң болады. Ықтималдылық мұндай жағдайда
қадамына тең және бағыты оң болады. Ықтималдылық мұндай жағдайда

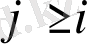 (1. 1. 6)
(1. 1. 6)
осылайша
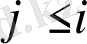 болғандағы
болғандағы
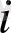 дің ауыспалы ықтималдылығын ойша шығаруға болады
дің ауыспалы ықтималдылығын ойша шығаруға болады
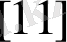 :
:
 ,
,
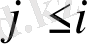 (1. 1. 7)
(1. 1. 7)
Радиоактивті ыдырау.
Радий қандайда бір
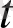 уақыттан кейін
уақыттан кейін
 радонға айналатындығын білеміз. Осындай айналу кезінде
радонға айналатындығын білеміз. Осындай айналу кезінде
 бөлігі пайда болады. Егер атомы
бөлігі пайда болады. Егер атомы
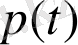 ықтималдылығына тәуелді емес және
ықтималдылығына тәуелді емес және
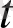 уақытта
уақытта
 атомына айналса, онда
атомына айналса, онда
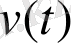 саны уақытта ыдырағанда
саны уақытта ыдырағанда
 атомына айналады,
атомына айналады,
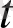 уақыттағы
уақыттағы
 бөлшегінің сандық иіні Пуассон заңы бойынша үлестіреміз:
бөлшегінің сандық иіні Пуассон заңы бойынша үлестіреміз:
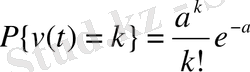
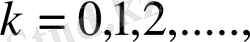 (1. 1. 8)
(1. 1. 8)
мұндағы
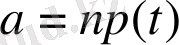 ,
,
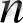 -
-
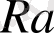 атомының алғашқы саны.
атомының алғашқы саны.
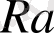 атомынан қалған сандар
атомынан қалған сандар
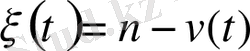
Егер
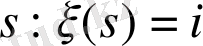 моментінде радий саны белгілі болса, онда
моментінде радий саны белгілі болса, онда
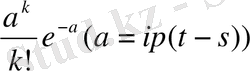 ықтималдылығының
ықтималдылығының
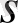 және
және
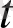 арасында
арасында
 -бөлігінің
-бөлігінің
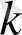 мәні шығады, осылайша ауыстырмалы ықтималдылықтың
мәні шығады, осылайша ауыстырмалы ықтималдылықтың
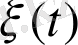 марковтік кездейсоқ процессі
марковтік кездейсоқ процессі
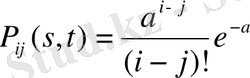
 (1. 1. 9)
(1. 1. 9)
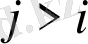 болғанда
болғанда
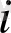 жағдайынан
жағдайынан
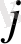 жағдайына ауысу мүмкін емес екені белгілі және
жағдайына ауысу мүмкін емес екені белгілі және
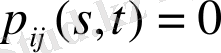
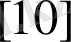 .
.
Күту уақытының айнымалы жағдайы.
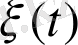 - бірыңғай Марков тізбегі болсын. Егер
- бірыңғай Марков тізбегі болсын. Егер
 Марков моментінің жүйесі тіркелген болсын, онда
Марков моментінің жүйесі тіркелген болсын, онда
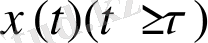 мұнан бұлайғы шығарылу кезінде
мұнан бұлайғы шығарылу кезінде
 моментіне тәуелді емес, егер бастапқы уақыт моменті
моментіне тәуелді емес, егер бастапқы уақыт моменті
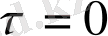 болса
болса
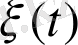 процесінен кейін
процесінен кейін
 -да сол заңдылыққа бағынады.
-да сол заңдылыққа бағынады.
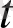 үзіліссіз деп алып қарастырсақ, кейбір
үзіліссіз деп алып қарастырсақ, кейбір
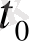 уақыт моментінде (
уақыт моментінде (
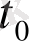
 0 деп алып) процесс жағдайы
0 деп алып) процесс жағдайы
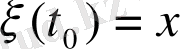 екені белгілі. Бұл жағдайды өзгертсек кездейсоқ момент пайда болады.
екені белгілі. Бұл жағдайды өзгертсек кездейсоқ момент пайда болады.
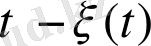 ауыспалы процес моментіне дейінгі жаңа
ауыспалы процес моментіне дейінгі жаңа
 күту мерзіміндегі айнымалы жағдай деп атаймыз.
күту мерзіміндегі айнымалы жағдай деп атаймыз.
Ықтималдылық
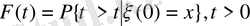 (1. 1. 10)
(1. 1. 10)
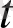 күш теңсіздігінің функциясы
күш теңсіздігінің функциясы
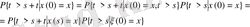 (1. 1. 11)
(1. 1. 11)
теңдеуін функцияналды қанағаттандырады.

кез келген
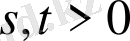 . Сондықтан
. Сондықтан
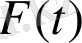 ықтималдылығы экспоненциялды функция болуы керек
ықтималдылығы экспоненциялды функция болуы керек
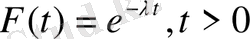
мұндағы
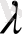 - тұрақты теріс емес сан.
- тұрақты теріс емес сан.
Осылайша
 уақыт күтімі
уақыт күтімі
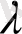 параметріндегі ықтималдылықтың көрсеткіштік үлестірімі болады.
параметріндегі ықтималдылықтың көрсеткіштік үлестірімі болады.
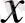 жағдайына сәйкес келетін
жағдайына сәйкес келетін
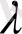 тұрақтысы ауыспалы тығыздық деп аталады.
тұрақтысы ауыспалы тығыздық деп аталады.
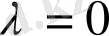 болғанда
болғанда
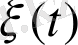 құбылысы
құбылысы
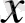 жағдайында қалады,
жағдайында қалады,
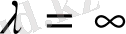 болғанда
болғанда
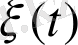 құбылысы
құбылысы
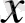 жағдайынан тез шығады,
жағдайынан тез шығады,
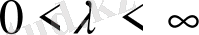 болғандағы ықтималдылық
болғандағы ықтималдылық
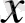 жағдайында
жағдайында
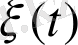 құбылысы
құбылысы
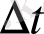 уақыт ішінде аз аралыққа өзгереді
уақыт ішінде аз аралыққа өзгереді
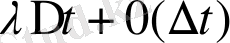
мұндағы
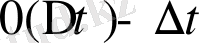 уақытымен салыстырғанда кіші ретті.
уақытымен салыстырғанда кіші ретті.
Дискрет моментінің
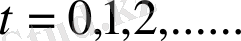 жүйесінде уақыт жиілігін
жүйесінде уақыт жиілігін
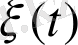 процес жағдайына ауыстырғанда «қадам санын»
процес жағдайына ауыстырғанда «қадам санын»
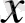 жағдайындағы
жағдайындағы
 -дан жаңа жағдайға дейін қарастырамыз
-дан жаңа жағдайға дейін қарастырамыз
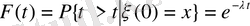
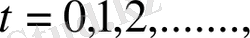 (1. 1. 12)
(1. 1. 12)
мұндағы
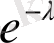 -
-
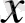 жағдайындағы бір қадамды ауыспалы ықтималдылық
жағдайындағы бір қадамды ауыспалы ықтималдылық
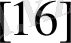 .
.
Мысал. Радиоактивті құбылыстың ыдырауы.
Сырттай сызылған жоғарғы ықтималдылық моделінің радиоактивті ыдырауы Ra радияның Rn радонға айналуы, мұндай ауысым Ra
 Rn екі жағдайдағы атомдардың біріңғай Марков құбылысын қолданады. Ra
Rn екі жағдайдағы атомдардың біріңғай Марков құбылысын қолданады. Ra
 Rn мүмкін ауысым болып табылады. Егер алғашқы уақыт моменті
Rn мүмкін ауысым болып табылады. Егер алғашқы уақыт моменті
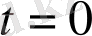 болса Ra атомының мөлшері
болса Ra атомының мөлшері
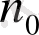 тең болады, онда
тең болады, онда
 -бөлшегіндегі
-бөлшегіндегі
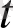 уақытта
уақытта
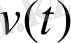 саны
саны
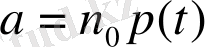 параметріндегі Пуассон үлестірімін қолданады
параметріндегі Пуассон үлестірімін қолданады
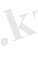
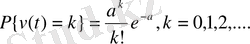 (1. 1. 13)
(1. 1. 13)
Бұл жердегі
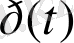 -
-
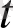 уақыттағы Ra жағдайына өту ықтималдылығы. Бұл ықтималдылық мынадай түрге келеді.
уақыттағы Ra жағдайына өту ықтималдылығы. Бұл ықтималдылық мынадай түрге келеді.
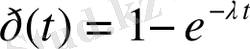
мұндағы
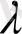 - Ra
- Ra
 Rn әр атомына сәйкес келетін кеңістіктегі ауысым т. с. с.
Rn әр атомына сәйкес келетін кеңістіктегі ауысым т. с. с.
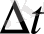 уақытындағы кіші аралықтағы Ra
уақытындағы кіші аралықтағы Ra
 Rn ауыспалы ықтималдылық
Rn ауыспалы ықтималдылық
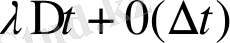 болады.
болады.
Қандайда бір
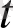 уақыт өткен соң радия мөлшерін қарастырамыз. Егер
уақыт өткен соң радия мөлшерін қарастырамыз. Егер
 -бөлшегіндегі сан
-бөлшегіндегі сан
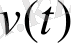 тең болса, онда Ra атомының қалдығы
тең болса, онда Ra атомының қалдығы
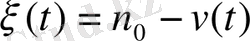 .
.
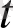 уақыттан кейінгі радия мөлшері орташа болады.
уақыттан кейінгі радия мөлшері орташа болады.
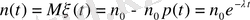
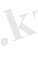 (1. 1. 14)
(1. 1. 14)
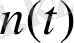 функциясының экспоненциялды сипаты Т уақытта алғашқы радия мөлшерінің жартысы ыдырайды, Т болғанда
функциясының экспоненциялды сипаты Т уақытта алғашқы радия мөлшерінің жартысы ыдырайды, Т болғанда
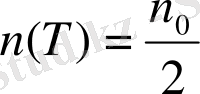
абсолютті тұрақты болады. Бұл тұрақтылық жартылай ыдырау деп аталады, және ол ауыспалы тығыздықтың Ra
 Rn ұмтылуы
Rn ұмтылуы
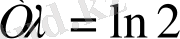 теңдігімен байланысты
теңдігімен байланысты
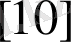 .
.
- Колмагоров теңдеуі.
Марков тізбегіндегі
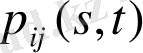 ауыспалы ықтималдылық мына шарттарды қанағаттандырады
ауыспалы ықтималдылық мына шарттарды қанағаттандырады
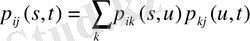
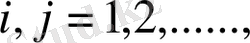 (1. 1. 15)
(1. 1. 15)
мұндағы
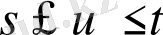 аралығында жатады.
аралығында жатады.
Бірыңғай марков тізбегі болсын. Егер оны
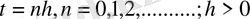 дискрет моментінде қарастырсақ, онда
дискрет моментінде қарастырсақ, онда
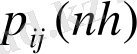 ықтималдылығының «бір қадамдық ауысымыда» бірдей анықталады.
ықтималдылығының «бір қадамдық ауысымыда» бірдей анықталады.
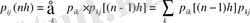
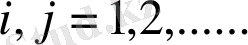 , (1. 1. 16)
, (1. 1. 16)
барлық жағдай үшін
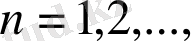
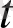 уақытын үзіліссіз етіп алмастыралық
уақытын үзіліссіз етіп алмастыралық
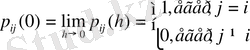
Бұл үзіліссіздіктің қасиетінің ауыспалы ықтималдылығы
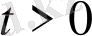 дифференциялдауында бірыңғай Марковтік тізбегі үзіліссіз болады, әрдайым бірыңғай шекте қолданылады
дифференциялдауында бірыңғай Марковтік тізбегі үзіліссіз болады, әрдайым бірыңғай шекте қолданылады
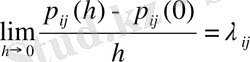
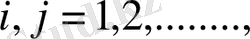 (1. 1. 17)
(1. 1. 17)
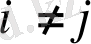 болғанда
болғанда
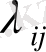 ақырлы болады.
ақырлы болады.
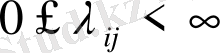
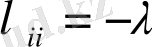
мұндағы
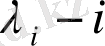 жағдайындағы ауыспалы тығыздық
жағдайындағы ауыспалы тығыздық
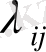 коэффициенті
коэффициенті
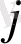 жағдайының
жағдайының
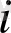 жағдайындағы ауыспалы тығыздығы
жағдайындағы ауыспалы тығыздығы
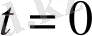 болғанда жүйе
болғанда жүйе
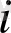 жағдайында болады., егер
жағдайында болады., егер
 жағдайындағы
жағдайындағы
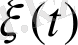 құбылысының бірінші шығу моменті болса, ал
құбылысының бірінші шығу моменті болса, ал
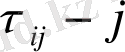 жағдайына бірінші түскен момент болса, онда
жағдайына бірінші түскен момент болса, онда
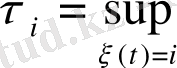
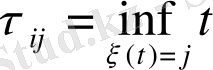
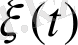 тізбегінде
тізбегінде
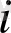 жағдайынан шықса
жағдайынан шықса
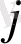 жағдайына баратыны белгілі
жағдайына баратыны белгілі
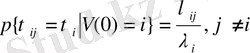 (1. 1. 18)
(1. 1. 18)
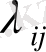 ауыспалы тығыздығы мына теңсіздікті қанағаттандырады
ауыспалы тығыздығы мына теңсіздікті қанағаттандырады
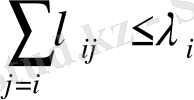
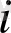
 1, 2, . . . , (1. 1. 19)
1, 2, . . . , (1. 1. 19)
және осы теңдігі орындалса
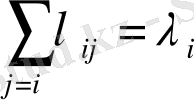
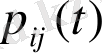 ауыспалы ықтималдылық қайтымды жүйедегі Колмагоровтің дифференциялдық теңдеуін қанағаттандырады
ауыспалы ықтималдылық қайтымды жүйедегі Колмагоровтің дифференциялдық теңдеуін қанағаттандырады

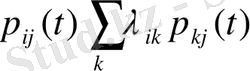
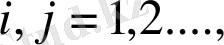 (1. 1. 20)
(1. 1. 20)
Мысал. Пуассон процессі.
Бірыңғай дербес оқиғалар жиынын қарастыралық.
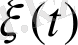 -
-
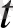 уақытындағы оқиғаның мәні Марков құбылысы болады,
уақытындағы оқиғаның мәні Марков құбылысы болады,
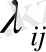 ауыспалы тығыздыққа сәйкес келетін
ауыспалы тығыздыққа сәйкес келетін


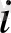 жағдайынан келесі
жағдайынан келесі
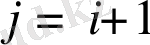 (
(
 ) жағдайына өтуге болады.
) жағдайына өтуге болады.
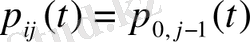 екені белгілі. Айталық
екені белгілі. Айталық
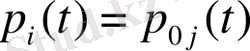
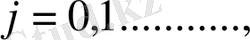
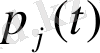 функциясы үшін Колмагоровтің дифференциялдық теңдеуі келесідей
функциясы үшін Колмагоровтің дифференциялдық теңдеуі келесідей
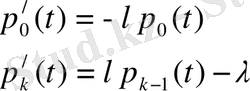
егер
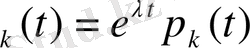 функциясымен алмастырсақ келесідей теңдеу аламыз
функциясымен алмастырсақ келесідей теңдеу аламыз
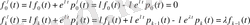
мұндағы
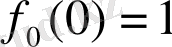 және
және
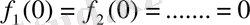
Дифференциялдық теңдеу түрі
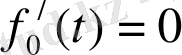
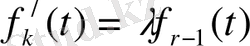
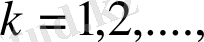
Көрсетілгендей бастапқы шарттардан келесідей шешім аламыз
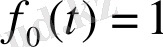
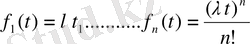 (1. 1. 21)
(1. 1. 21)
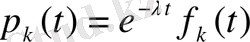 алғашқы функциясынан қайтқанда
алғашқы функциясынан қайтқанда
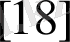
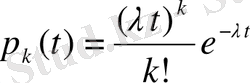
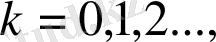 (1. 1. 22)
(1. 1. 22)
Мысал.
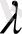 параметріндегі Пуассон құбылысын құрайтын жүйені есептеп шартты топ алынады шарттардың әрқайсысынан кездейсоқ
параметріндегі Пуассон құбылысын құрайтын жүйені есептеп шартты топ алынады шарттардың әрқайсысынан кездейсоқ
 уақыты шығады, мұндағы
уақыты шығады, мұндағы
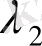 параметрінің экспоненциялды заңдылығы бойынша
параметрінің экспоненциялды заңдылығы бойынша
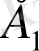 - еркін жағдай,
- еркін жағдай,
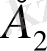 - бос емес жағдайындағы қызыметін қарастыралық.
- бос емес жағдайындағы қызыметін қарастыралық.
Кез келген
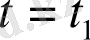 белгіленген уақыт моментінен осы уақытқа дейінгі пайда болған шарттың сипатына тәуелді емес. Егер жүйе
белгіленген уақыт моментінен осы уақытқа дейінгі пайда болған шарттың сипатына тәуелді емес. Егер жүйе
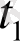 уақыт моментінде
уақыт моментінде
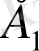 жағдайында жатса, онда алдыңғы жағдай бұрынғысына тәуелді емес болады.
жағдайында жатса, онда алдыңғы жағдай бұрынғысына тәуелді емес болады.
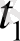 және
және
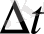 уақыт аралығында
уақыт аралығында
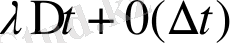 ықтималдылығы
ықтималдылығы
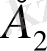 жағдайына өтеді.
жағдайына өтеді.
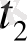 моментіндегі жүйе
моментіндегі жүйе
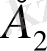 жағдайында жатса
жағдайында жатса
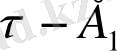 -дің
-дің
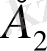 жағдайына ауысқандағы кездейсоқ моменті болсын. Экспоненциялды заң бойынша уақыт үлестірімі теңдеуіне келеді:
жағдайына ауысқандағы кездейсоқ моменті болсын. Экспоненциялды заң бойынша уақыт үлестірімі теңдеуіне келеді:
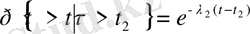
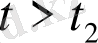
осы жерден
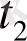 және
және
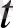 аралығындағы
аралығындағы
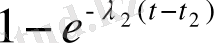 ықтималдылығы
ықтималдылығы
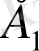 жағдайына өтетіндігін көреміз және
жағдайына өтетіндігін көреміз және
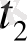 моментіне дейін оның шығарылуына тәуелді емес.
моментіне дейін оның шығарылуына тәуелді емес.
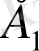 және
және
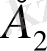 жағдайына сәйкес келетін
жағдайына сәйкес келетін
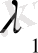 және
және
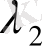 ауыспалы тығыздығы Марков құбылысының эвалюция жүйесін айтады.
ауыспалы тығыздығы Марков құбылысының эвалюция жүйесін айтады.
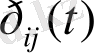 ауыспалы ықтималдылық болсын.
ауыспалы ықтималдылық болсын.
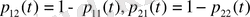 қарастыратын жағдайымыз және Колмагоровтің дифференциялдық теңдеуі келесідей екіге бөлінеді:
қарастыратын жағдайымыз және Колмагоровтің дифференциялдық теңдеуі келесідей екіге бөлінеді:
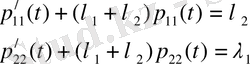 (1. 1. 23)
(1. 1. 23)
және шешімі мынандай формуламен жазылады
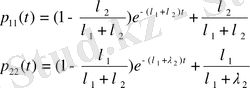 (1. 1. 24)
(1. 1. 24)
құбылыстың орнықтылығы. Үзіліссіз
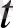 уақытында
уақытында
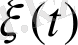 біріңғай Марков тізбегі
біріңғай Марков тізбегі
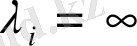 сәйкес келетін ауыспалы тығыздықтың лездік жағдайы деп атаймыз.
сәйкес келетін ауыспалы тығыздықтың лездік жағдайы деп атаймыз.
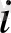 күйіне түскенде жүйе тез ауысады
күйіне түскенде жүйе тез ауысады
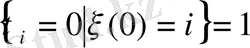
мұндағы
 жағдайынан шыққан бірінші момент. Кез келген
жағдайынан шыққан бірінші момент. Кез келген
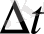 уақыт аралығында жағдайдан шығып қайта оралады.
уақыт аралығында жағдайдан шығып қайта оралады.
 аралығындағы
аралығындағы
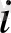 жағдайында барлық болған уақыты
жағдайында барлық болған уақыты
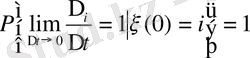
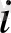 жағдайын орнықты деп атаймыз, егер
жағдайын орнықты деп атаймыз, егер
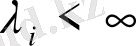 болса
болса
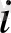 -күйінің орнықты жағдайында ықтималдылықтың оң аралығы жатады:
-күйінің орнықты жағдайында ықтималдылықтың оң аралығы жатады:
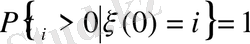
Ықтималдылықтың кез келген уақыт аралығында бір сан бір жағдайдан екінші жағдайға өтсе Марков тізбегі орнықты деп аталады.
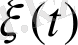 Марков тізбегі лездік жағдайға жатпайды,
Марков тізбегі лездік жағдайға жатпайды,
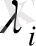 - ауыспалы тығыздығы ақырлы және
- ауыспалы тығыздығы ақырлы және
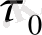 - бастапқы
- бастапқы
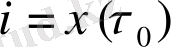 жағдайындағы бірінші шыққан момент т. с. с.
жағдайындағы бірінші шыққан момент т. с. с.
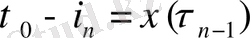 жағдайындағы шыққан момент.
жағдайындағы шыққан момент.
Тізбектің орнықты болуы үшін 1 ықтималдылықтың шартын орындау жеткілікті:
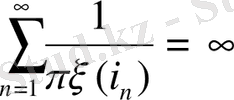
жағдайының ақырлы тізбегі орнықты болады
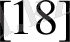 .
.
Мысал. Көбейту құбылысы.
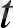 уақыт моментіндегі
уақыт моментіндегі
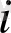 саны көбейсе
саны көбейсе
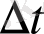 аралығында тағы да бір
аралығында тағы да бір
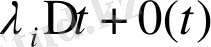 ықтимал бөлшек қосылады, ал қатар шамасы
ықтимал бөлшек қосылады, ал қатар шамасы
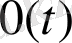 болады. Мұндай құбылыс
болады. Мұндай құбылыс
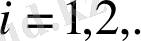 жағдайындағы Марков тізбегін құрады және ауыспалы тығыздығы
жағдайындағы Марков тізбегін құрады және ауыспалы тығыздығы
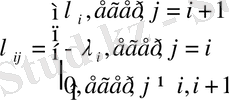
Орнықтылық шарты бойынша ақырсыз ауыспалы сан жүйесіне кеткен
 уақыт ықтималджылығы ақырсыз деп аталады. Бұл шарт
уақыт ықтималджылығы ақырсыз деп аталады. Бұл шарт
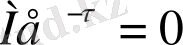 шартына пара-пар. Егер
шартына пара-пар. Егер
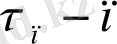 жағдайынан шыққан момент болса, онда
жағдайынан шыққан момент болса, онда
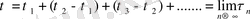
болады.
мұндағы
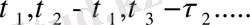 -тәуелсіз кездейсоқ шама,
-тәуелсіз кездейсоқ шама,
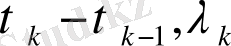 параметрлі үлестірімі көрсеткішіне тәуелді. Сондықтан
параметрлі үлестірімі көрсеткішіне тәуелді. Сондықтан
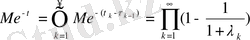 (1. 1. 25)
(1. 1. 25)
орнықты болады егер тек мына шарт орындалса
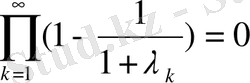
бұл шарт былай бөлінеді
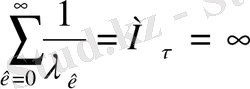
осылайша Пуассон құбылысына қарастырған мысалымыздың шешімін аламыз.
- Минимал ауыспалы ықтималдылық.
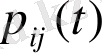 ауыспалы ықтималдылықтың орнықтылық шарты Колмагоровтің диференциялдық теңдеуінің жалғыз шешімі болып табылады. Кез келген тізбек үшін олай емес, бірақ
ауыспалы ықтималдылықтың орнықтылық шарты Колмагоровтің диференциялдық теңдеуінің жалғыз шешімі болып табылады. Кез келген тізбек үшін олай емес, бірақ
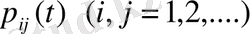 минимальді шешімі бар болады, кез келген
минимальді шешімі бар болады, кез келген
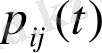 шешімі үшін бұл теңдеулердегі барлық
шешімі үшін бұл теңдеулердегі барлық
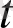 үшін келесі теңдік орындалады
үшін келесі теңдік орындалады
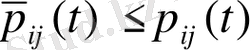
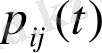 құрамдас минималді шешім
құрамдас минималді шешім
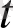 уақыттағы
уақыттағы
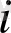 -дан
-дан
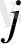 -ға дейінгі ауыспалы ықтималдығы шығады.
-ға дейінгі ауыспалы ықтималдығы шығады.
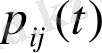 минималды шешімі
минималды шешімі
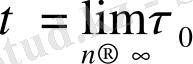 моментіндегі тізбегін айтады, мұндағы
моментіндегі тізбегін айтады, мұндағы
 моментіндегі ауысым санын білдіреді
моментіндегі ауысым санын білдіреді
 .
.
Мысал. Құбылысты көбейту. Ауыспалы тығыздық мынадай болсын
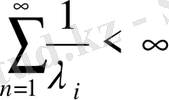
және бастапқы моментте бір бөлшек болсын. Ақырсыз көп болатын тағы да бір жағдай енгіземіз.
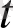 уақытында бұл жағдай
уақытында бұл жағдай
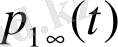 оң ықтималдылықтан өтетін құбылыс, яғни ауыспалы тығыздыққа сәйкес келетін барлығы нөлге тең және
оң ықтималдылықтан өтетін құбылыс, яғни ауыспалы тығыздыққа сәйкес келетін барлығы нөлге тең және
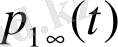 үшін дифференциялдық теңдеуі мына түрге келеді
үшін дифференциялдық теңдеуі мына түрге келеді
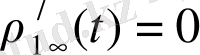
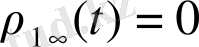 (1. 1. 26)
(1. 1. 26)
Негізінде
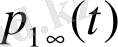 теңдеудің шешімі болмайтындығы белгілі, сондықтан
теңдеудің шешімі болмайтындығы белгілі, сондықтан
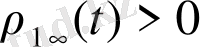 . Минимальды шешімі жүйедегі
. Минимальды шешімі жүйедегі
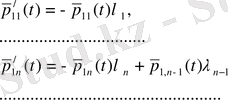 (1. 1. 27)
(1. 1. 27)
теңдеуінен біртіндеп анықталады.
1. 2 Бірыңғай марков тізбегін класстарға бөлу
Қайтымды және қайтымсыз жағдай.
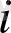 жағдайының нәтижесі қайтымсыз деп аталады, ақырлы
жағдайының нәтижесі қайтымсыз деп аталады, ақырлы
 уақыт аралығында ықтималдылық 1 жүйесі бұл жағдайда қайтпайды.
уақыт аралығында ықтималдылық 1 жүйесі бұл жағдайда қайтпайды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz