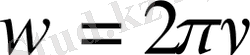Механика және молекулалық физика: кинематика, динамика, сұйықтар мен газдар механикасы және термодинамика
МЕХАНИКА
§ 1. Кинематика
Жалпы жағдайда түзу сызықты қозғалыстың жылдамдығы
\[v={\frac{d s}{d t}}\]
Үдеуі
\[a={\frac{d v}{d t}}\]
Equation. 3
Түзу сызықты бір қалыпты қозғалыс болғaн жағдайда
υ
= const және
\[{\mathcal Q}\,\]
Equation. 3 = 0.
Түзу сызықты бір қалыпты айнымалы қозғалыс кезінде
\[s=v_{0}t+{\frac{a t^{2}}{2}}\]
,
\[u\implies_{0}\vdash Q f\]
,
\[{\mathcal Q}\,\]
= const.
Бұл теңдеулерде үдеу
\[{\mathcal Q}\,\]
бір қалыпты үдемелі қозғалыс кезінде оң болады да, ал бір қалыпты баяу қозғалыс кезінде теріс болады.
Қисық сызықты қозғалыс кезінде толық үдеу
\[a={\sqrt{a_{t}+a_{n}}}\]
,
мұндағы
\[{\mathcal Q}\,\]
t
- тангенциал үдеу, ал
\[Q_{n}\]
- нормаль (центрге тартқыш үдеу) үдеу, сондықтан
\[{\mathcal Q}\,\]
t
\[={\frac{d v}{d t}}\]
,
\[Q_{n}\]
\[={\frac{v^{\ 2}}{R}}\]
мұндағы
υ -
қозғалыстың жылдамдығы, ал
R
- берілген нүктедегі траекторияның қисықтық радиусы.
Айналмалы қозғалыста жалпы жағдайында бұрыштық жылдамдық
\[w={\frac{d\phi}{d t}}\]
ал бұрыштық үдеу
\[e={\frac{d\omega}{d t}}\]
Бip қалыпты айналмалы қозғалыс кезінде бұрыштық жылдамдық
\[w={\frac{2\pi}{T}}\]
мұндағы Т - айналу периоды, ν - айналу жиілігі, яғни (бірлік уақыт ішіндегі айналым саны)
Бұрыштық жылдамдықтың сызықтық жылдамдықпен өз ара байланысы мына қатынаспен анықталады:
\[\mathcal{U}\supset\mathcal{D}\setminus\mathcal{D}\]
Тангенциал және нормаль үдеулер айналмалы қозғалыста мынадай түрде көрсетілуі мүмкін:
\[a_{t}=\]
\[\varepsilon\cdot\mathbb{R}\]
,
\[{\boldsymbol{a}}_{n}=\]
\[\;\varrho\,\upsilon\,\upsilon\,\upsilon\,\upsilon\,\upsilon\,\upsilon\,\upsilon\,\]
(6 - кестеде ілгерілемелі қозғалыс теңдеуінің айналмалы қозғалыс теңдеуімен салыстырмасы берілген.
6 - кесте
Ілгерілемелі қозғалыс:
Ілгерілемелі қозғалыс
Айналмалы қозғалыс:
Айналмалы қозғалыс
Ілгерілемелі қозғалыс:
Бір қалыпты
Ілгерілемелі қозғалыс:
\[\subseteq\bigcup\overset{\in}{\subseteq}(\]
Айналмалы қозғалыс:
\[j_{\mathbf{\delta}}=\omega\mathbf{t}\]
Ілгерілемелі қозғалыс:
\[v=\mathbb{C O P I S}\]
Айналмалы қозғалыс:
\[\omega=C\mathrm{OPIS}\]
Ілгерілемелі қозғалыс:
a=0
Айналмалы қозғалыс:
ε=0
Ілгерілемелі қозғалыс:
Бір қалыпты айнымалы
Ілгерілемелі қозғалыс:
\[s=v_{0}t+{\frac{a t^{2}}{2}}\]
Айналмалы қозғалыс:
\[j_{\mathbf{\delta}}=w_{0}\mathbf{t}+\frac{e\mathbf{t}^{2}}{2}\]
Ілгерілемелі қозғалыс:
\[\displaystyle u=v_{o}+\Delta t\]
Айналмалы қозғалыс:
\[w=w_{0}+\varepsilon\mathbb{I}\]
Ілгерілемелі қозғалыс:
а=соnst
Айналмалы қозғалыс:
ε=соnst
Ілгерілемелі қозғалыс:
Бір қалыпсыз
Ілгерілемелі қозғалыс:
s=f(t)
Айналмалы қозғалыс:
φ=f(t)
Ілгерілемелі қозғалыс:
\[v={\frac{d s}{d t}}\]
Айналмалы қозғалыс:
\[w={\frac{d\phi}{d t}}\]
Ілгерілемелі қозғалыс:
\[\Omega={\frac{\mathrm{d}{\boldsymbol{v}}}{\mathrm{dt}}}={\frac{\mathrm{d}^{2}{\boldsymbol{S}}}{\mathrm{dt}^{2}}}\]
Айналмалы қозғалыс:
\[e={\frac{\mathrm{d}w}{\mathrm{dt}}}={\frac{\mathrm{d}^{2}\phi}{\mathrm{dt}^{2}}}\]
§ 2. Динамика
Динамиканың негізгі заңы (Ньютонның екінші заңы) мына теңдеумен өрнектеледі:
F dt = d(mυ) .
Егер масса тұрақты болса, онда
\[\mathbf{f}=\mathbf{m}{\frac{\mathrm{d}{\boldsymbol{\omega}}}{\mathrm{dt}}}=\mathbf{m}{\boldsymbol{\hat{e}}}\]
,
Мұндағы
а
-
F
күштің әсерінен массасы
m
дененің алатын үдеуі.
F
күштің s орын ауыстырғандағы жұмысы мынадай формуламен өрнектелуі мүмкін:
\[A=\!\!\!\!\!\int_{\gamma}J.d S\]
мұндағы
F
s
- жол бағытындағы күштің проекциясы,
ds
- жол учаскесінің шамасы. Иптегралдау s жолына тұтас таралуға тиіс. Кей жағдайда орын ауыстыруға тұрақты бұрыш жасай әсер ететін тұрақты күшке мынаны аламыз:
\[A=F s\cos{\alpha}\]
,
мұндағы
\[{\mathcal{Q}}\]
-
F
күш пен s жүрген жол арасындағы бұрыш.
Қуат төмендегі формуламен анықталады:
\[N={\frac{d A}{d t}}\]
.
Тұрақты қуат жағдайында
\[N={\frac{A}{t}}\]
,
мұндағы А -
t
уақыт ішіндегі істеліпетін жұмыс.
Сондай-ақ қуатты мынадай формуламен анықтауға болады:
N = Fυ
cos a,
яғни қуат қозғалыс жылдамдығының қозғалыс бағытындағы күш проекциясының көбейтіндісімен анықталады.
v
жылдамдықпен қозғалатын, массасы
т
дененің кинетикалық энергиясы мынаған тең:
\[M_{\mathrm{k}}={\frac{\mathrm{m\ell}\ ^{2}}{2}}\]
.
Әсер етуші күштің сипатына қарай, потенциалық энсргияның формуласы әр түрлі болады.
Изоляцияланған системада оған енетін барлық денелердің қозғалыс мөлшері тұрақты болып қалады, яғни
\[\Pi\vert u_{1}+\Pi u_{2}+\ldots+\Pi\vert_{1}v_{n}=C\mathrm{ODIS}\]
.
Массалары
т
1
және m
2
екі денепің серпімсіз центрлік соғылысқан кезде осы денелердің соғылысқаннан кейінгі қозғалысының жалпы жылдамдығын төмендегі формуламен табуға болады:
\[\mathrm{U}={\frac{\Pi\psi_{1}+\Pi_{2}v_{2}}{\Pi\ +\Pi_{2}}}\]
.
мұндағы
\[{\boldsymbol{v}}_{\perp}\]
- соғылғанға дейінгі бірінші дененің жылдамдығы, ал
\[{\boldsymbol{v}}_{\textbf{2}}\]
- соғылғанға дейінгі екінші дененің жылдамдығы.
Денелер серпімді центрлік соғылысқан кезде әр түрлі жылдамдықпен қозғалатын болады. Соғылысқаннан кейінгі бірінші дененің жылдамдығы
\[\mathbf{u}_{1}={\frac{(\mathbf{m}_{1}+\mathbf{m}_{2})u_{1}+2\mathbf{m}_{2}v_{2}}{\mathbf{m}_{1}+\mathbf{m}_{2}}}\]
,
соғылысқаннан кейінгі екінші дененің жылдамдығы
\[u_{2}={\frac{({\bf{m_{1}}}-{\bf{m_{2}}})u_{2}+2{\bf{m_{1}}}_{1}}{{\bf{m_{1}}}+{\bf{m_{2}}}}}\]
.
Қисық сызықты қозғалыста материялық нүктеге әсер ететін күшті екі құраушы күшке жіктеуге болады: тангенциаль және нормаль күштерге.
Нормаль құраушы
\[\mathbf{f}_{n}={\frac{\mathbf{m}v^{2}}{\mathbf{R}}}\]
центрге тартқыш күш болады. Мұнда υ - массасы
т
дененің қозғалысының сызықтық жылдамдығы,
R
- берілген пүктедегі траекторияның қисықтық радиусы.
Серпімді деформация
х
туғызатын күш деформацияның шамасына пропорционал, яғни
F = kx,
мұндағы
k
- бірге тең деформация туғызатын, сан жағынан күшке тең коэффицент (деформация коэффициенті) .
Серпімді күштің потенциал энергиясы
\[W_{n}=\frac{k x^{2}}{2}\]
Екі материялық нүкте (яғни өлшемдері олардың өз ара қашықтықтарына қарағанда кішкене больп келетін денелер) бір-біріне мынадай күшпен тартылады:
\[F=\gamma\,{\frac{m_{1}m_{2}}{R^{2}}}\]
,
мұндағы
\[{\mathcal{V}}\]
тартылыс тұрақтысы немесе гравитациялық тұрақты, бұл тең
\[{\mathcal{V}}\]
= 6, 67 • 10
-11
м
3
/кг • сек
2
, т
1
және
т
2
-
өз ара әсер ететін материялық нүктелердің массасы;
R
- олардың ара қашықтығы. Бұл заңды біртекті шарларға да қолдануға болады. Сонда
R
- олардың центрлерінің ара қашықтығы болады.
Тартылыс күшінің потенциалық энергиясы
\[W_{n}=-\gamma\frac{m_{1}m_{2}}{R}\]
«Минус» таңбасы
R-
\[\infty\]
болғандағы өз ара әсер етуші екі денелердің потенциалық эпергиясының нолге тең болатындығын көрсетеді, ал бұл денелер бір-біріне жақындағанда потенциал энергия кемиді.
Кеплердің үшінші заңы мына түрде болады:
\[{\frac{T_{1}^{2}}{T_{2}^{2}}}={\frac{R_{1}^{3}}{R_{2}^{3}}}\]
мұндағы
Т
1
және
Т
2
- планеталардың айналып шығу периоды,
R
1
жәпе
R
2
- олардың орбиталарының үлкен жарты остері. Дөңгелек орбита жағдайында үлкен жарты осьтің ролін орбита радиусы атқарады.
§ 3. Қатты денелердің айналмалы қозғалысы
Қандай болмасын, айналу осімен салыстырғандағы
F
күштің
М
моменті төмендегі формуламен анықталады:
\[M=F l\]
мұндағы
l
-айналу осінен бойымен күш әсер ететін түзуге дейінгі қашықтық.
Материялық нүктенің қандай болмасын айналу осіне қатысты инерция моменті деп мына шаманы айтамыз:
\[J=m r^{2}\]
,
мұндағы
т
- материялық нүктенің массасы, ал
\[{\hat{\mathcal{J}}}^{\Phi}\]
- нүктенің осьтен қашықтығы.
Қатты дененің оның айналу осі арқылы алынған инерция моменті
\[J=\mathbf{\partial}\mid r^{2}d m\]
мұнда интегралдауды дененің барлық көлемі арқылы жүргізу керек. Интегралдау жүргізе отырып мынадай формулалар алуға болады:
1) өзінің осі арқылы алынған тұтас біртекті цилиндрдің инерция моменті
\[J={\frac{1}{2}}m R^{2}\]
мұндағы
R
- цилиндрдің радиусы, ал m - оның массасы.
2) цилиндр осінс қатысты ішкі радиусы
R
1
және сыртқы радиусы
\[\textstyle{\mathcal{D}}\]
2
қуыс цилиндрдің (құрсаудың) инерция моменті
\[J=m{\frac{R_{1}^{2}+R_{2}^{2}}{2}}\]
,
жұқа қабырғалы қуыс цилиндрдің
R
1
\[\frac{\rho^{\operatorname*{ma_{12}}\!\omega}}{\equiv\operatorname*{man}_{n}}\]
R
2
= R
және
3) шардың центрінен өтетін оське қатысты радиусы біртекті шардың инерция моменті
\[J={\frac{2}{5}}m R^{2}\]
4) стерженьнің ортасынан өткен оське қатысты біртекті стерженьнің инерция моменті оның
\[\frac{\overline{{{\beta}}}}{\widehat{\beta}}\]
ұзындығына перпендикуляр
\[J={\frac{1}{12}}m l^{2}\]
.
Егер қандай болмасын дененің ауырлык центрінен өтетін оське қатысты инерция момснті
\[\mathcal{J}\]
0
белгілі болса, онда бірішні оське параллель болатын кез келген ось арқылы алынған инерция моментін Штейнер формуласымен табуға болады:
\[J=J_{\mathrm{0}}+m d^{2}\]
,
мұндағы
т
- дененің массасы, ал
d
- ауырлық центрінен айналу осіне дейінгі қашықтық.
Айналмалы қозғалыс динамикасының негізгі заңы төмендегі теңдеумеи көрсетіледі:
\[M{\mathcal{M}}{\mathcal{U}}={\mathcal{U}}(\mathcal{I}_{c0})\]
,
мұндағы
М
- инерция моменті
\[{\mathcal{J}}\]
-ге тең денеге түсірілген күш моменті;
\[{\mathcal{O}}\]
- дененің айналысының бұрыштық жылдамдығы. Егер
\[\mathcal{J}\]
= const болса, онда
\[M=J{\frac{d w}{d t}}=J e\]
мұндағы
\[\begin{array}{c}{{\underline{{{\mathcal{C}}}\Phi}}}\\ {{\underline{{{\theta}}}\Omega^{\prime}}}\\ {{\underline{{{\theta}}}\Gamma}}\end{array}\]
- айналыс моментінің
М
әсерінен дененің алатын бұрыштық үдеуі.
Айналатын дененің кинетикалық энергиясы
\[W_{k}={\frac{J\omega^{2}}{2}}\]
мұндағы
\[\mathcal{J}\]
- дененіц инерция моменті, ал
\[{\mathcal{O}}\]
- оның бұрыштық жылдамдығы.
Айналмалы қозғалыс динамикасы теңдеуінің ілгерілемелі қозғалыстыц теңдеуімен салыстырмасы 7-кестеде берілген.
Физикалық маятниктің кіші тербелістерінің периоды
\[T=2\pi{\sqrt{\frac{J}{m d g}}}\]
мұндағы
\[\mathcal{J}\]
- маятниктің осіне қатысты инерция моменті,
m
- маятниктің массасы,
d
- айналу осінен ауырлық центрге дейінгі қашықтық,
g
- ауырлық күшінің үдеуі.
7-кесте
Ілгерілемелі қозғалыс
Айналмалы қозғалыс
Ілгерілемелі қозғалыс:
Ньютонның екінші заңы
Ілгерілемелі қозғалыс:
\[F\Im\ell=m u_{2}-m v_{1}\]
Айналмалы қозғалыс:
\[M\mathrm{D}t=J w_{2}-J\omega_{1}\]
Ілгерілемелі қозғалыс:
немесе
Айналмалы қозғалыс:
немесе
Ілгерілемелі қозғалыс:
\[F=m a\]
Айналмалы қозғалыс:
\[M=J\varepsilon\]
Ілгерілемелі қозғалыс:
Қозғалыс мөлшерінің сақталу заңы
\[\sum m v\,=\,c o n s t\]
Айналмалы қозғалыс:
Қозғалыс мөлшері моментінің сақталу заңы
\[\sum J_{\mathrm{r}}=c o n s t\]
Ілгерілемелі қозғалыс:
Жұмыс және кинетикалық энергия
Ілгерілемелі қозғалыс:
\[A=F S={\frac{m u_{2}^{2}}{2}}-{\frac{m v_{1}^{2}}{2}}\]
Айналмалы қозғалыс:
\[A=M j\ =\frac{J w_{2}^{2}}{2}-\frac{J\omega_{1}^{2}}{2}\]
§ 4. Газдар мен сұйықтардың механикасы
Сығылмайтын идеал сұйықтың қалыптасқан қозғалысы үшін Бернулли теңдеуі алынады.
\[p+{\frac{r\,v^{2}}{2}}+\rho g h=c o n s t\]
.
Мұндағы
\[\mathcal{P}\]
- сұйықтың тығыздығы, υ - трубаның берілген қимасындағы сұйық қозғалысының жылдамдығы,
\[{\mathcal{J}}_{\bar{\imath}}\]
- трубаның берілген қимасының кейбір деңгейден алынған биіктігі және
р
- қысым. Бериуллидің теңдеуінен, кішкентай тесіктен сұйықтың ағып шығу жылдамдығы υ
=
\[\scriptstyle{\sqrt{2g h}}\]
мұндағы
\[{\mathcal{J}}_{\bar{\boldsymbol{I}}}\]
-
тесіктен жоғары қарай алынған сұйықтың бетіне дейінгі биіктік. Қандайда бол-масын трубаның көлденең қимасынан бірдей көлемдегі сұйық өтетін болғандықтан,
\[S_{1}u_{1}=S_{2}v_{2}\]
болады, мұндағы υ
1
және υ
2
- көлденең қималарының ауданы, S
1
және
S
2
трубаның екі қимасынан өтетін сұйықтардың жылдамдығы.
Тұтқыр сұйықта (немесе газда) құлайтын шарикке жасалатын кедергі күш
Стокс
формуласымен анықталады:
\[F=6m r\nu\]
,
мұндағы
\[{\mathcal{I}}{\mathcal{I}}\]
- сұйықтың немесе газдың ішкі кедергісінін коэффициенті (динамикалық тұтқырлық),
\[{\hat{\mathcal{N}}}^{\Phi}\]
- шариктің радиусы, υ - оның жылдамдығы. Стокстың заңы тек қана ламинарлық қозғалыс үшін берілген. Ламинарлық қозғалыс кезінде
t
уақыт ішімде радиусы
\[{\hat{\mathcal{J}}}^{\Phi}\]
және ұзындығы
\[\frac{\overline{{{\beta}}}}{\overline{{{\beta}}}}\]
капиляр түтік арқылы ағып өтетін сұйықтың (газдың) көлемі
Пуазейль
формуласымен анықталады
\[V={\frac{p r^{4}t\Delta p}{8l\eta}}\]
мұндағы
\[{\mathcal{I}}{\mathcal{I}}\]
- сұйықтың (газдың) динамикалық тұтқырлығы,
\[\Lambda_{\bf d}\]
р - түтік ұштарындағы қысымдардың айырымы.
Сұйық (газ) қозғалысының сипаты Рейнольдстің өлшемсіз саны арқылы анықталады
\[\mathrm{Re}={\frac{D\nu r}{h}}={\frac{D\nu}{\nu}}\]
,
мұндағы
D
- сұйықтықпен (газбен) ағатын дененің сызықтық мөлшерін сипаттайтын шама, υ - сұйықтың ағу жылдамдығы,
\[\mathcal{P}\]
- тығыздық,
\[{\mathcal{I}}{\mathcal{I}}\]
- динамикалық тұтқырлық. Қатынас v =
\[\mathcal{P}\]
/p кинематикалық тұтқырлық деп аталады.
Ламинарлық қозғалыстан турбулентті қозғалысқа ауысуды анықтайтын Рейнольдс санының кризистік мәні әр түрлі формалы денелерде түрліше болады.
Есептер шығару кезінде қажет нұсқаулар
Еселік және үлестік бірліктерін жасауға арналған косымшалар
1 - кесте
Қосымшалар
Caн мәндері
Қысқаша белгілер
Косымшалар
Сан мәндері
Кысқаша белгілер
Қосымшалар:
Атто
Фемто
Пико
Нано
Микро Милли Санти
Caн мәндері:
10
-18
10
-15
10
-12
10
-9
10
-6
10
-3
10
-2
Қысқаша белгілер:
а
ф
п
н
мк
м
с
Косымшалар:
Деци
Дека
Гекто
Кило
Мега
Гига
Тера
Сан мәндері:
10
-1
10
1
10
2
10
3
10
6
10
9
10
12
Кысқаша белгілер:
д
да
г
к
М
Г
Т
МЕХАНИКАЛЫҚ БІРЛІКТЕР
2-кесте
Шамалар жәнеоның белгілері:
Шамалар және
оның белгілері
Бірліктерді анықтауғаарналған теңдеулер:
Бірліктерді анықтауға
арналған теңдеулер
Өлшеу бірліктері:
Өлшеу бірліктері
Бірліктердің кысқаша белгілері:
Бірліктердің кысқаша белгілері
Шамалардың өлшем-ділігі:
Шамалардың өлшем-
ділігі
Шамалар жәнеоның белгілері:
Негізгі бірліктер
Шамалар жәнеоның белгілері:
Ұзындық l
Бірліктерді анықтауғаарналған теңдеулер:
Өлшеу бірліктері:
метр
Бірліктердің кысқаша белгілері:
м
Шамалардың өлшем-ділігі:
L
Шамалар жәнеоның белгілері:
Масса
m
Бірліктерді анықтауғаарналған теңдеулер:
Өлшеу бірліктері:
килограмм
Бірліктердің кысқаша белгілері:
кг
Шамалардың өлшем-ділігі:
М
Шамалар жәнеоның белгілері:
Уақыт
t
Бірліктерді анықтауғаарналған теңдеулер:
Өлшеу бірліктері:
секунд
Бірліктердің кысқаша белгілері:
сек
Шамалардың өлшем-ділігі:
Т
Шамалар жәнеоның белгілері:
Туынды бірліктер
Шамалар жәнеоның белгілері:
Аудан S
Бірліктерді анықтауғаарналған теңдеулер:
S=
l
2
Өлшеу бірліктері:
квадрат метр
Бірліктердің кысқаша белгілері:
м
2
Шамалардың өлшем-ділігі:
L
2
Шамалар жәнеоның белгілері:
Көлем
V
Бірліктерді анықтауғаарналған теңдеулер:
V=
\[{J}^{3}\]
Equation. 3
Өлшеу бірліктері:
куб метр
Бірліктердің кысқаша белгілері:
м
3
Шамалардың өлшем-ділігі:
L
3
Шамалар жәнеоның белгілері:
Жиілік ν
Бірліктерді анықтауғаарналған теңдеулер:
\[\nu={\frac{N}{t}}\]
Өлшеу бірліктері:
герц
Бірліктердің кысқаша белгілері:
Гц
Шамалардың өлшем-ділігі:
T
-1
Шамалар жәнеоның белгілері:
Бұрыштық жылдамдық ω
Бірліктерді анықтауғаарналған теңдеулер:
Өлшеу бірліктері:
радиан секундқа
Бірліктердің кысқаша белгілері:
рад/сек
Шамалардың өлшем-ділігі:
T
-1
Шамалар жәнеоның белгілері:
Бұрыштық үдеу ε
Бірліктерді анықтауғаарналған теңдеулер:
\[e={\frac{\mathrm{D}\omega}{\Delta\mathbf{t}}}\]
Өлшеу бірліктері:
радиан квадрат секундка
Бірліктердің кысқаша белгілері:
paд/ceк
2
Шамалардың өлшем-ділігі:
T
-2
Шамалар жәнеоның белгілері:
Сызықтық жылдамдық υ
Бірліктерді анықтауғаарналған теңдеулер:
\[v={\frac{\mathbf{D}\lambda}{\Delta\mathbf{t}}}\]
Өлшеу бірліктері:
метр секундка
Бірліктердің кысқаша белгілері:
м/сек
Шамалардың өлшем-ділігі:
LT
-1
Шамалар жәнеоның белгілері:
Сызықтық үдеу
a
Бірліктерді анықтауғаарналған теңдеулер:
\[\mathbf{\hat{e}}={\frac{\mathbf{D}v}{\Delta\mathbf{t}}}\]
Өлшеу бірліктері:
метр квадрат секундка
Бірліктердің кысқаша белгілері:
м/сек
2
Шамалардың өлшем-ділігі:
LT
-2
Шамалар жәнеоның белгілері:
Тығыздық ρ
Бірліктерді анықтауғаарналған теңдеулер:
\[\rho={\frac{m}{V}}\]
Өлшеу бірліктері:
килограмм куб метрге
Бірліктердің кысқаша белгілері:
кг/м
3
Шамалардың өлшем-ділігі:
L
-3
M
Шамалар жәнеоның белгілері:
Күш
Ғ;
салмақ
Р
Бірліктерді анықтауғаарналған теңдеулер:
F=ma
Өлшеу бірліктері:
Ньютон
Бірліктердің кысқаша белгілері:
Н
Шамалардың өлшем-ділігі:
LMT
-2
Шамалар жәнеоның белгілері:
Меншікті салмақ
γ
Бірліктерді анықтауғаарналған теңдеулер:
\[\gamma={\frac{\mathrm{{D}}}{\mathcal{V}}}\]
Өлшеу бірліктері:
Ньютон куб метрге
Бірліктердің кысқаша белгілері:
Н[м
3
Шамалардың өлшем-ділігі:
L
-2
MT
-2
Шамалар жәнеоның белгілері:
Қысым р
Бірліктерді анықтауғаарналған теңдеулер:
\[p={\frac{F}{S}}\]
Өлшеу бірліктері:
Ньютон квадрат метрге
Бірліктердің кысқаша белгілері:
H/м
2
Шамалардың өлшем-ділігі:
L
-1
MT
-2
Шамалар жәнеоның белгілері:
Қозғалыс мөл-шері
L
Бірліктерді анықтауғаарналған теңдеулер:
L=m∆V=
F∆t
Өлшеу бірліктері:
Килограмм-метр секундқа
Бірліктердің кысқаша белгілері:
кг • м/сек
Шамалардың өлшем-ділігі:
LMT
-1
Шамалар жәнеоның белгілері:
Инерция моменті
J
Бірліктерді анықтауғаарналған теңдеулер:
J=ml
2
Өлшеу бірліктері:
килограмм-квадрат метрге
Бірліктердің кысқаша белгілері:
кг·м
2
Шамалардың өлшем-ділігі:
L
2
M
Шамалар жәнеоның белгілері:
Жұмыс және энергия
А
Бірліктерді анықтауғаарналған теңдеулер:
A=Fl
Өлшеу бірліктері:
Джоуль
Бірліктердің кысқаша белгілері:
Дж
Шамалардың өлшем-ділігі:
L
2
MT
-2
Шамалар жәнеоның белгілері:
Қуат N
Бірліктерді анықтауғаарналған теңдеулер:
\[N={\frac{A}{t}}\]
Өлшеу бірліктері:
Ватт
Бірліктердің кысқаша белгілері:
Вт
Шамалардың өлшем-ділігі:
L
2
MT
-3
Шамалар жәнеоның белгілері:
Динамикалық тұтқырлық η
Бірліктерді анықтауғаарналған теңдеулер:
\[h={\frac{F}{S}}{\frac{\mathrm{D}}{\Delta x}}\]
Өлшеу бірліктері:
ньютон-секунд квадрат метрге
Бірліктердің кысқаша белгілері:
Н·с/м
2
Шамалардың өлшем-ділігі:
L
-1
MT
-1
Шамалар жәнеоның белгілері:
Кинематикалық тұтқырлық
Бірліктерді анықтауғаарналған теңдеулер:
\[n={\frac{h}{\rho}}\]
Өлшеу бірліктері:
квадрат метр секундқа
Бірліктердің кысқаша белгілері:
м
2
/сек
Шамалардың өлшем-ділігі:
L
2
T
-1
5 -кесте
Шамасы:
Шамасы
Өлшеу бірліктері және оның ХЖ бірліктерімен байланысы:
Өлшеу бірліктері және оның ХЖ бірліктерімен байланысы
Шамасы:
Ұзындық
Масса
Жазық бұрыш
Аудан
Көлем
Күш
Кысым
Жүмыс, энергия, жылу мөлшері
Қуат
Динамикалық
тұтқырлық
Кинематикалық тұтқырлық
Өлшеу бірліктері және оның ХЖ бірліктерімен байланысы:
сантиметр(см) = 10-2м
1 микрометр (микрон) ; 1
мкм=10
-6
м
1 ангстрем (А) = 10
-10
м
1 грамм (г) = 10
-
3
кг
1 тонна
(т)
=10
3
кг
1 центнер
(ц) = 10
2
кг
1 массаның атомдық бірлігі (1 м. а. б. ) = 1, 66• 10
-27
кг
1 градус (°) =
\[\frac{\pi}{180}\]
рад
1 минут (') =
\[\frac{\pi}{180}\]
• 10
-2
рад
1 секунд (") =
\[\frac{\pi}{648}\]
• 10
-3
рад
1 айналым
(айн)
=2 π
рад
1 ар=100
м
2
1 гектар (га) = 10
4
м
2
1 литр (л) = 1, 28 • 10
-3
м
3
1 дина
(дин)
= 10
-5
Н
1 килограмм-күш
(кГ)
=9, 81 Н
1 тонна-күш (Г) =9, 8·10
3
Н
1
дин/см
2
=9, 8 Н/м
2
1 кГ/м
2
=9, 81 Н/м
2
1 миллиметр сынап бағанасы
(мм
сын. бағ. ) = = 133, 0
Н/м
2
1 миллиметр су бағанасы
(мм
су. бағ. ) =9, 81
Н/м
2
1 техникалық атмосфера
(атм) = \ кГ/см
2
=0, 981 •
10
5
Н/м
2
1 физикалық атмосфера (атм) = 1, 013· 10
5
Н/м
2
(«физикалық атмосфераның» жүйеден тыс бірлігі ГОСТ 7664-61 -де жоқ)
1 эрг =10
-7
Дж
1 кГДж=9, 81 Дж
1 Ватт-сағат
(Вm • caғ)
=3, 6· 10
3
Дж
1 электрон-вольт (1
эв)
= 1, 6 • 10
-19
Дж
1 калория (кал) =4, 19
Дж
1 килокалория (1
ккал)
=4, 19 • 10
3
Дж
1 физикалық литр-атмосфера
(л • атм) =
= 1, 01 • 10
2
Дж
1 техникалык литр-атмосфера (л· атм) =98, 1
Дж
1
эрг /сек
=1 0
-7
Вт
1 килограмм-күш метр секундқа
(кГм/сек)
= 9, 81 Вт
1 ат күші (а. к. ) =75
кГм/сек=735 Вт
1 пуаз (пз) =0, 1 Н·сек/м
2
=0, 1 кг/м •
сек
1 стокс
(ст) =
10
-4
м
2
/сек
II ТАРАУ
МОЛЕКУЛАЛЫҚ ФИЗИКА ЖӘНЕ ТЕРМОДИНАМИКА
ЖЫЛУ БІРЛІКТЕРІ
§ 5. Молекула-кинетикалық теорияның және термодинамиканың физикалық негіздері
Идеал газдар Менделеев - Клапейрон күйінің теңдеуіне бағынады:
\[p V={\frac{M}{\mu}}R T\]
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Механика: кинематика, динамика, импульс пен энергия заңдары, айналушы денелер механикасы және салыстырмалық теория элементтері Механика: кинематика мен динамика негіздері, Ньютон заңдары және энергияның сақталу заңы Классикалық механика: кинематика, динамика және механикалық энергия Механика негіздері: кинематика, динамика, Ньютон заңдары, энергия, импульс және тербелістер Классикалық механика: кинематика, динамика, энергия және реактивті қозғалыс Теориялық механика: кинематика, статика және динамика бөлімдері бойынша курстық жұмыс Молекулалық-кинетикалық теория және термодинамика: идеал газдар мен күй теңдеулері Молекулалық физика және термодинамика: атомдық-молекулалық теория, идеал газ және молекула-кинетикалық теория Физика пәнінде деңгейлеп-саралап оқытудың әдістемелік негіздері: механика және кинематика Кинематика, динамика және арнайы салыстырмалылық теориясының негізгі қағидалары


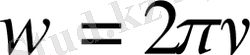 ,
,