Кеңейтілген натурал сандар жиынының қасиеттері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 157 бет
Таңдаулыға:

КЕНЖЕБЕКОВА РАБИГА ИБРАХИМОВНА

МАТЕМАТИКА НЕГІЗДЕРІ

Шымкент,2023

Дәріс №1. Математиканың бастауыш курсын пән ретінде оқуды ұйымдастыру

Дәріс мақсаты: Математиканың бастауыш курс негіздері пәні, оның қажеттілігі, актуальдылығы, қолданысы туралы қарастыру.
1.1. Курстың объектісі, пәні, міндеттері
1.2. Курстың мазмұны
1.3. Курстың басқа оқу пәндерімен байланысы
Қазақстан Республикасының Білім туралы заңында Білім беру жүйесінің басты міндеті - ұлттық және жалпы азаматтық құндылықтар, ғылым мен практика жетістіктері негізінде жеке адамды қалыптастыруға және кәсіби шыңдауға бағытталған білім алу үшін қажетті жағдайлар жасау, оқытудың жаңа технологияларын енгізу, білім беруді ақпараттандыру, халықаралық ғаламдық коммуникациялық желілерге шығу деп, білім беру жүйесін одан әрі дамыту міндеттері көзделеді.
Білім алу, шеберлікке, іс-әрекет дағдыларына үйрету мен меңгеру барысы және адамды өмір мен еңбекке бейімді етіп даярлаудың негізгі құралы - оқыту. Оқыту барысының нәтижесінде білім беру мен тәрбие мақсаттары жүзеге асырылады. Түрлі оқу орындарындағы оқыту - білім берудің басты жолы, сол сияқты оқу отбасында, ондірісте, жұмыста т.б. күнделікті адамның тіршілік және қызмет барысындағы жағдайларды іске асып отырады.
Оқытудың мазмұны мен сипаты қоғамның материалдық және мәдени даму дәрежесіне сай белгіленеді. Оқудың мақсаты мен мазмұны, оны ұйымдастырудың түрлері мен әдістері адамзат қоғамының даму кезеңдеріндегі қоғамдық қатынастар негізінде, жалпы білімге, адамдардың даярлығы негізінде қойылатын талаптардың сипатына және оқыту жөніндегі педагогикалық идеяларға сай өзгеріп отырады.
Білім беру саласындағы болып жатқан өзгерістер соңғы жылдары педагогикалық білім алатын болашақ мамандарға, олардың кәсіби дайындықтарына елеулі талаптар қоюда. Әсіресе, бастауыш сынып мұғалімдерін даярлауға қойылатын талаптар күрделі де сан-салалы болып отыр. Себебі бастауыш сынып мұғалімі - жас ұрпақ бойына ең алғашқы білім негіздерін сіңіретін, олардың дағдылары мен машықтарын дұрыс бағытта қалыптасуын қамтамасыз ететін, ізгілікті және отаншылдық қасиеттерге баулитын тұлға.
Мемлекеттік білім стандартында бастауыш сынып мұғалімдеріне кәсіби жан-жақты теориялық және практикалық білім мен дағдыларды, әлеуметтік және гуманитарлық пәндер негіздері өнерпаздық қабілеттерді, оқыту мен ақпараттық технологияларды пайдалану дағдыларын, іскерлік машықтарын жан-жақты меңгерту көзделген.
Математиканың бастауыш курсының негіздері пәні студенттерге математиканы табысты оқытып-үйретуге, оқушыларды бастауыш математика курсы ұғымдарының негізгі мектепте қолданылу мүмкіндіктерін көре білуге қажет болатын даярлықты қамтамасыз етеді.
Математиканың бастауыш курсының негіздері пәні бастауыш сыныптар мұғалімдерінің кәсіби даярлығы жүйесіндегі арнаулы пән ретінде өткен ғысырдың ХХ-сыншы жылдары жоғары мектеп жұмысын ұйымдастырудың бірыңғай мемлекеттік принциптері анықталған кезде қалыптаса бастады.
Бастауыш сынып мұғалімдеріне кәсіби теориялық білім педагогика, психология, әдістеме ғылымдарын оқытумен бірге бастауыш сыныптардағы негізгі пәндер - қазақ (орыс) тілі, математика, ана тілі, бейнелеу өнері, дүние тану, музыка т.б. ғылымдардың негіздерін меңгерту арқылы да белгілі.
Осы тұрғыда бастауыш сыныпта берілетін математикалық білім мазмұны мен оқушылардың дайындықтарының міндетті деңгейіне қойылатын талаптар басты назарға алынады. Мектептің бастауыш сатысында берілетін математикалық білім мазмұны қарапайым математикалық түсініктерді қалыптастыру, сандар нумерациясы, алгебра элементтері, геометрия элементтері, шамалар және оның өлшем бірліктері деп аталатын бөлімдерден тұрады.
Әрбір мұғалім математика пәнінде оқушыларды терең ойлай білуге, олардың шығармашылық қабілеттерін дамытып, өз бетінше жұмыс жасай білуге үйрету мақсатын қояды. Бұл мақсатты орындау, яғни оқушылардың білім, білік, дағдысын, өзіндік танымын қалыптастыру - нақты ұйымдастырылған кезеңдер арқылы жүзеге асырылатын күрделі үрдіс. Жалпыға міндетті орта білім стандарттарында (жалпы бастауыш білім) білім объектісі ретінде - білім мазмұны алынған болса, өркениетті елдердің тәжірибесінде білім объектісі ретінде - оқыту нәтижесі алынған. Осыған орай білім мазмұнын жаңарту мен оқытудың инновациялық әдістерін өндіру бүгінгі күннің талабы болып отыр.
Білім сапасы оның төрт сипатын (білім - құндылық, білім - жүйе, білім - процесс, білім - нәтиже) біртұтас қарастыра отырып, олардың ішінде білімнің құндылық ретіндегі және білімнің нәтиже ретіндегі сипатына мән берумен тікелей байланысты.
Математика білім саласы бойынша күтілетін нәтижелер білім мазмұнының жетекші компоненттері және білім, түсіну, қолдану, жоғарғы сипаттағы біліктер деп аталатын категориялар арқылы бейнелеген оқу материалдарын меңгеру деңгейлерін ескере отырып анықталады. Мұнда басты есте болатын нәрсе - оқушылардың математикалық мәдениетін көтеру, математиканы оқып- үйренуге ынталандыру, нақты дағдыларды бекіту.
Курсты оқытудың әдістері: ғылыми-педагогикалық әдебиеттерді, бағдарламаларды, математикадан оқулықтар мен оқу-әдістемелік құралдарды теориялық талдау; педагогикалық эксперимент; бақылау; озат педагогикалық тәжірибені оқып-үйрену және жалпылау; әңгіме; анкетк; тест және т.б.
Математиканы оқыту теориясы мен технологиясы педагогикалық ғылым және оқу пәні ретінде ұзақ уақыт қалыптасты және дамыды. Оның даму кезеңдері Қазақстан Республикасы мектептік білім берудің реформалаумен тығыз байланысты. XX - шы ғасырдың 70-ші жылдарына дейін оқытылған арифметика курсы өзіне алгебра және геометрия элементтерін біріктіре отырып, математиканы оқыту әдістемесінің негізі болады. Математиканың әдістемесіне 80-90 жылдардағы математиканы оқыту процесіне дамыта оқыту теориясының, білімнің дидактикалық бірліктерін ірілендіру теориясының енгізілуіне орай елеулі өзгерсітер енді. Математика негіздері пәні педагогикалық ғылым саласы ретіндегі объектісі, пәні, міндеттері мен ғылыми-зерттеу әдістері, оның басқа ғылым салаларымен (философиямен, логикамен, математикамен, педагогикамен, психологиямен және т.б) байланысты.
Қазіргі кезде білім беру саласында болып жатқан ауқымды өзгерістер түрлі ынталы бастамалар мен түрлендірулерге кеңінен жол ашуда. Осы қарастырылған мәселелер реті болашақ бастауыш сынып мұғалімдерінің оқушылардың математикалық білімін тереңдете және кеңейте түсуімен байланысты шығармашылық ізденісін қамтамасыз етеді. Кіші жастағы оқушыларға математиканы оқытудың әдістемелік жүйесінің өзіндік ерекшеліктерін сипаттайтын әдістемелік ережелер, сондай-ақ оқытуға тұлғалық-іскерлік және дамытушылық тұрғыдан қарау әдістемелік құрал мазмұнын құрайды.
Дәріс №2.

Жиындар. Жиындарға қолданылатын амалдар және олардың заңдары
Дәріс мақсаты: Жиындар, жиын элементтеріне анықтама беріп, таныстыру. Жиындарға амал қолда білуге үйрету
Жиын уғымы. Жиынның элементтері
Жиындардың жазылуы мен оның берілу тәсілдері
Бос жиын
Тең жиындар
Ішкі жиындар
Жиындардың графикалық иллюстрациясы (сипаттамасы.)
Жиындарға қолданылатын амалдар.
а) Жиындардың қиылысуы
ә) Жиындардың бірігуі
б) Жиынның толықтауышы. Жиындардың айырмасы

в) Жиындардың декарттық көбейтіндісі

Жиын математиканың негiзгi ұғымдарының бiрi. Оны тек мысалдармен түсiндiруге болады. Мысалы, кiтап бетiндегi әрiптер жиыны, институттағы студенттер жиыны, т.с.с Жиынды құрайтын барлық заттарды оның элементтерi деп атайды. Жиын элементтерiнiң табиғаты әртүрлi болады: елдер, жұлдыздар, үйлер, сандар, геометриялық денелер, жан-жануарлар т.с.с. Жиынды латын алфавитiнiң бас әрiптерiмен белгiлейдi.
Мысалы: M={a, b, c, d, e} түріндегі жазылу элементтері a, b, c, d, e әрiптерiнен құралған жиынды көрсетедi. Бұл жиынды элементтерiнiң орналасу ретiн өзгертiп те жазуға болады. a элементi M жиынынына тиiстi немесе a заты M жиынының элементi сөйлемдерi а символымен белгiленедi. Ал k символы k заты M жиынының элементi емес деп оқылады.
Элементтердiң санына қарай жиындар шектеулi және шектеусiз жиындар болып бөлiнедi. Мысалы, кейбiр институттағы студенттер жиыны шектеулi. Ал шектеусiз жиындарға өзiмiзге белгiлi мынадай сандық жиындар мысал болады:
N - натурал сандар жиыны,
No - кеңейтілген натурал сандар (теріс емес бүтін сандар) жиыны,
Z - бүтiн сандар жиыны,
Q - рационал сандар жиыны,
R - нақты сандар жиыны.
Математикада бiрде-бiр элементi жоқ жиынды да қарастырады. Ондай жиынды бос жиын дейдi. Бос жиынды символымен белгiлейдi. Мысалы, 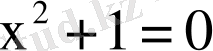теңдеуiнiң нақты шешiмдерiнiң жиыны бос жиын болады.
Жиынды оның барлық элементтерiн атау арқылы анықтауға болады. Жиынның осындай түрде берiлуi тек шектеулi жиындар үшiн орын алады.
Жиын барлық элементтеріне тән қасиетiн атау арқылы да берiледi. Онда жиын элементтерi сипаттайтын қасиетiмен берiлдi дейдi. Мысалы, 7-ден кiшi натурал сандар жиыны М берiлсiн. Бұл жиын элементтерiн сипаттайтын қасиет: жиын элементтерi натурал сандар және олар 7-ден кiшi. Бұл жиынды былай жазады M = {x xN, x7}.
Бiр жиынның өзi әртүрлi мiнездемелiк қасиеттері арқылы берiлуi мүмкiн. Мысалы, жоғарыда келтiрiлген M={x xN, x7} жиынын 0 және 7,5 сандарының арасында орналасқан натурал сандар жиыны ретiнде де анықтауға болады. Демек, M={x xN, 0x7,5}.
Көптеген есептер элементтерiнiң мiнездемелiк қасиетi белгiлi болған жағдайда, жиынды анықтауға әкелiп соғады. Мысалы, 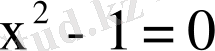теңдеуiнiң барлық түбiрлерiнiң жиынын анықтайық. Бұл жиын элементтерiнiң қасиетi 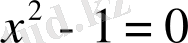теңдеуiнiң түбiрi болуы.
Яғни A= {x x(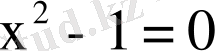)} түрiнде жазылады.
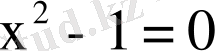теңдеуiн шешейiк. Сонда 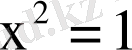болғандықтан, түбiрлерi х1 = -1, х2 = 1 болады. Сондықтан A={ - 1, 1}.
Егер А және В жиындары бiрдей элементтерден тұрса, оларды тең жиындар деп, A=В түрiнде жазады. Мысалы, A={5, 6, 7, 8, 9} және В={7, 5, 9, 6, 8} жиындары тең жиындар. Олар тек 5, 6, 7, 8, 9 элементтерiнен тұрады.
Егер А жиынның әрбiр элементi В жиынының да элементi болса, онда А жиын В жиынның бөлiгi (iшкi жиыны) дейдi. Мұны АВ немесе ВА деп белгiлейдi және А жиыны В жиынның iшкi жиыны деп оқиды. Мысалы, В - институттағы барлық студенттер жиыны, ал А - топ студенттерi жиыны дейiк. Сонда А жиыны В жиынының бөлiгi болатыны анық. Демек АВ.
Әрбiр жиын өзiнiң iшкi жиыны (бөлiгi) болады, яғни АА деп есептеледi. Осы сияқты, бос жиын кез келген А жиынының iшкi жиыны болады, яғни А. А жиынының А-дан өзгеше бос емес кез келген В iшкi жиыны оның меншiктi бөлiгi (iшкi жиыны) деп, ал А мен iшкi жиындары меншiктi емес бөлiктерi (iшкi жиындары) деп аталады. Мысалы, M={x xN, x4} жиынының меншiктi iшкi жиындары {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, ал меншiктi емес жиындары {1, 2, 3} мен болады.
Кез келген n элементтен тұратын жиынның 2n iшкi жиыны болады.
Егер. ВА және АВ болса, онда А=В болады. Сонымен бiрге, егер АВ және ВС болса, АС болады.
Егер U жиынның ғана iшкi жиындары қарастырылатын болса, ондай жиынды универсал жиын деп атайды. Айталық, А - институттағы қыздар жиыны, В - сол институттағы спортшылар жиыны, ал С - сол институттағы ұлдар жиыны болсын. Сонда институттағы студенттер жиыны U универсал жиын, яғни АU, ВU, СU болады.
Жиындар арасындағы қатынастарды көрсету үшiн, кез келген жиынның элементтерiн тұйық контур iшiнде орналасқан нүктелер ретiнде қарастырады. Бұл контурдың iшкi нүктелерiн тiкелей бейнелеу қажет емес. А жиыны В жиынының меншiктi ішкі жиыны болатыныны 1-суреттегiдей кескінделеді.
B
A
U
A B
B
A
U
A B

1-сурет 2-сурет
U - универсал жиын төртбұрыш ретiнде кескінделеді (2-сурет). Мысалы, U - кiтапханадағы кiтаптар жиыны, ал А- математика пәнi кiтаптарының жиыны, В - Бастауыш мектеп журналының жиыны. Осылайша графиктiк кескiндеу әдiсi Эйлер-Венн дөңгелектерi немесе диаграммалары деп аталады.
А мен В жиындарына ортақ элеметтерден құрылған жиынды олардың қиылысуы деп атайды. А мен В жиынының қиылысуы АВ түрiнде белгiленедi. Мұндағы символы жиындардың қиылысуы белгiсi.
А В
А В

3-сурет
А мен В жиындарының қиысуын Эйлер-Венн дөңгелектері арқылы бейнелеуге болады (3-сурет). А мен В жиындарының ортақ элементерi болмаса, олардың қиылысуы бос жиын болады: АВ=. Бұл жиындарды қиылыспайды дейдi. Үш немесе бiрнеше жиындардың қиылысуы да жоғарыда айтылғандай анықталады.
Жиындардың қиылысуының қасиеттерi:
АВ=ВА (орын ауыстырымдылық)
(АВ)С=А(ВС) (терiмдiлiк)
Егер АВ болса, онда АВ=А болады.
Кез келген А жиыны үшiн АА=А, А= және АU=А болады.
Мысалы, А={x xR, 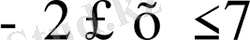}, В={x xR, }.
Осы екi жиынның қиылысуын табайық.
Шешуi. А және В жиынын сан өсiнде бейнелейiк. Сонда А жиыны шеткi нүктелерi - 2 және 7 де жататын кесiндiнi ал, В жиыны шеткi
4-сурет
10
7
3
-2
4-сурет
10
7
3
-2
нүктелерi 3 және 10 болатын кесiндiнi бейнелейдi. Ал осы екі жиынның қиылысуы: АВ қос сызықпен штрихталған (4-сурет) кесiндiні бередi.
А және В жиындарының кем дегенде бiрiнде жататын элементтерден құрылған жиынды, олардың бiрiгуi деп атайды. Оны АВ деп белгiлейдi. Мұндағы символы жиындарының бiрiгуінің белгiсi.
Жиындардың бiрiгуiнiң қасиеттерi:
1. АВ= ВА (орын ауыстырымдылық),
2. (АВ)C =A(ВC) (терiмдiлiк),
3. Егер. ВА болса, онда АВ=А болады.
4. а) А(ВС)=(АВ)(АС);
ә) А(ВС)=(АВ)(АС) (жиындардың қиылысуы мен бiрiгуiнiң арасындағы үлестiрiмдiлiк).
Мысалы, А={a, b, c, d, e, f} және В={d, e, f, n, m, k} болсын. Сонда осы жиындардың бiрiгуі АВ={a, b, c, d, e, f, n, m, k} болады. АВ жиыны 7-суретте Эйлер-Венн диаграммалары көмегiмен кесiкiнделген.

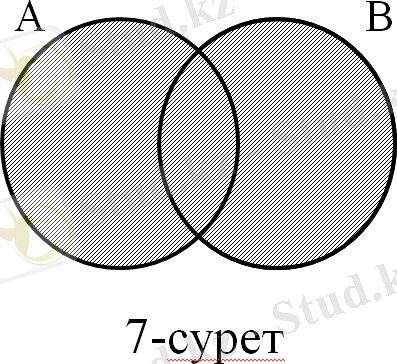
Егер А және В жиындары берiлсе, онда В жиынында жатпайтын А жиынының элементерінің жиынын олардың айырмасы деп айтады. Оны А\В=С деп жазады. Эйлер-Венн дөңгелектерімен 8-суретте кескiнделген.

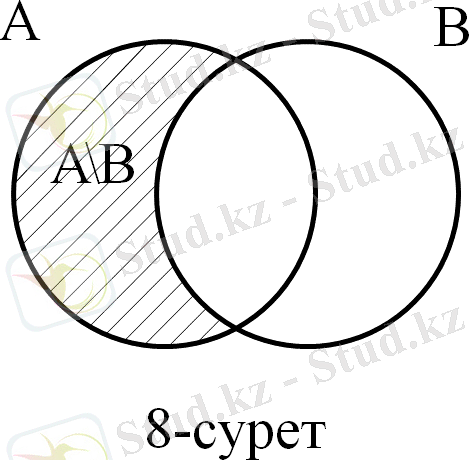
Мысалы, А={1, 2, 3, 4, 5} және В={2, 4, 6, 8} болса, А\В={1, 3, 5} болады. Сонымен А\В=A\(AB) болады. А\В жиынының кез келген x элементi А-да жатады, В-да жатпайды қасиетiне ие болады. А жиыны В-ның iшкi жиыны болсын. Сонда, А жиынының В-да жатпайтын элементтерiнiң жиынын В жиынының А-дағы толықтауышы деп атайды. Оны 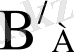символымен белгiлейдi. Мысалы, N - натурал сандар жиыны, Р - барлық жұп натурал сандар жиыны болса, онда Р - iшкi жиынының толықтауышы барлық тақ натурал сандар жиыны РN={1, 3, 5, ..., 2n - 1,...} болады. Универсал жиынының кез келген iшкi жиындары А, В және С үшiн төмендегі теңдiктер орындалады.
1) (АB)[] =А[]В[];
2) (АB)[] =А[]В[];
3) А\(ВС)=(A\B)(A\C);
4) А\(ВC)=(A\B)(A\C)=(A\B)\C
Берiлген жиынды өзара қос-қостан қиылыспайтын iшкi жиындарға бөлiктеу үшiн мынадай шарттар орындалуы керек:
Бөлiктердi құрайтын әрбiр iшкi жиын бос жиын емес.
Әрбiр iшкi жиындар өзара қиылыспайды.
Барлық iшкi жиындардың бiрiгуi берiлген жиынға тең.
Мысалы, X={бақ, бағбан, қар, бақташы, қарлы, пiсiру, пiскен} жиыны элементерiнiң арасында түбiрi бiрдей қатынасы берiлсе, осы қатынас арқылы X жиынын ішкі жиындарға бөліктеуге бола ма?
Шешуi. X1 жиынына түбiрi бақ болатын сөздер жиналады.
Х1={бақ, бағбан, бақташы};
Х2 жиынына түбiрi қар болатын сөздер жиналады.
Х2={қар, қарлы};
Х3 жиыныныа түбiрi пiс болатын сөздер жиналады.
Х3={пiсiру, пiскен} болады.
Х1, Х2 және Х3 жиындары бос емес, олар қос-қостан қиылыспайды, ал олардың бiрiгуi Х1Х2Х3=Х болатыны көрiніп тұр. Сонымен әр түрлi сөздер жиынында түбiрi бiрдей деген қатынас осы жиынды түбiрi бiрдей сөздер кластарына бөліктеуге мүмкiндiк бердi.
Кейбiр жағдайда, жиынды өзара қос-қостан қиылыспайтын iшкi жиындарға бөлiктеу мүмкiн болмайды.
Мысалы, барлық үшбұрыштар жиынын теңбүйiрлi үшбұрыштар жиыны және тiкбұрышты үшбұрыштар жиынына бөлiктеуге болмайды, өйткенi жоғарыдағы үш шарттың кейбiреуi орындалмайды.
№3 Дәріс
Жоспар:
Реттелген жұптар.
Кортеж.
Декарттық көбейтiндi.
Декарттық координаттар жүйесі

Айталық 35 саны берiлсiн. Бұл сан 3 және 5 цифрларымен жазылған. Олар белгiлi бiр анықталған ретпен алдымен 3, содан соң 5 цифры жазылған. Олардың орынын ауыстырсақ басқа 53 саны алынады. Сондықтан реттелген жұптар ұғымын енгiзуге тура келедi. х пен у шамаларын реттелген (х, у) түрiнде жазуға болады.
х пен у-тi (х, у) реттелген жұбының компоненттерi немесе координаттары деп атайды. (х1, у1) және (х2, у2) жұптары, х1=x2, у1=у2 болғанда ғана бiрi-бiрiне дәл келедi.
Кортеж ұғымын түсіндіру үшін параллелограмм деген сөздi құрайтын әрiптердiң жиынын жазайық. Ол {п, а, р, л, е, о, г, м} болады. Бiрақ параллелограмм сөзi дұрыс жазылуы үшiн, онда қолданылатын әрiптердi ғана емес, олардың жазылу ретiн де бiлу керек, демек әрiптердiң орналасу тәртiбi де ескерiледі. Математикада мұндай жағдайлар көптеп кездеседi. Мысалы, 15531122 санындағы цифрлар жиыны: {1, 5, 3, 2}. Бiрақ бұл сандағы цифрлар өзiнiң тұрған ретiне, орнына байланысты түрлi мағынаға ие. Айталық, сол жағынан санағанда бiрiншi 1-лiк 10 миллиондықты білдірсе, екінші 1-лiк 1 мыңдықты көрсетедi. Математикада мұндай реттелген жиынтықтарды кортеждер деп атайды. Кортеждiң әрбiр элементi оның компонентi немесе координаты деп аталады. Осы мысалдағы цифрлардың кортежi (1, 5, 5, 3, 1, 1, 2, 2) түрiнде жазылады. Кортеж координаттарының саны оның ұзындығы деп аталады. Мысалы (п, а, р, а, л, л, е, л, о, г, р, а, м, м) кортежiнiң ұзындығы 14-ке тең.
Кортеж ұғымын пайдаланып екi, үш, төрт, тіпті n жиындарының декарттық көбейтiндiсiн анықтауға болады.
Х және У жиындарының декарттық көбейтіндісі деп бірінші компоненті хХ, ал екінші компоненті уУ болатын барлық (х,у) жұптарының жиынын айтады, оны деп белгілейді.
А және В сандық жиындар болса олардың декарттық көбейтіндісі сандардың реттелген жұптарының жиыны болады. Әрбір жұпты жазықтықтағы нүктемен белгілесек, А және В жиындарының декарттық көбейтіндісін бейнелейтін фигура шығады. Мұны х пен у шамаларының реттелген (х,у) жұбы түрінде жазуға болады. х пен у-ті (х,у) реттелген жұбының компоненттері немесе координаттары деп атайды. (х1,у1) және (х2,у2) жұптары, х1=х2, у1=у2 болғанда ғана бірі-біріне дәл келеді.
Ал, (а1, а2, ..., аm) және (b1, b2, ..., bn) кортеждерi а1=b1, а1=b2, . . . , аm=bn болғанда ғана тең болады. Айталық А1, А2, ..., Аn жиындары элементерiнен ұзындығы n-ге тең 1-шi компонентi А1 жиынынан, 2-шi компонентi А2 жиынан, ... n-шi компонентi Аn жиынынан алынған кортеждер жасайық. Осылайша жасалған кортеждер жиынын А1, А2, ..., Аn жиындарының декарттық көбейтiндiсi деп атайды да, 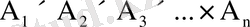деп белгiлейдi:
Егер ХхХ декарттық көбейтіндінің ішкі жиыны көрсетілсе, онда X жиынында катыс берілген деп есептеледі. Қатынасты Р, R, S, Q т.б. әріптерімен белгілеу және хРу, хRу, хSу т.с.с. түрінде жазу қабылданған.
Мысалы, А1={1; 2}, А2={3, 4}, А3={5; 6; 7} берiлсе,
А1 х А2 х А3 ={(1; 3; 5), (1; 3; 6), (1; 3; 7), (1; 4; 5), (1; 4; 6), (1; 4; 7),(2; 3; 5), (2; 3; 6), (2; 3; 7;), (2; 4; 5), (2; 4; 6), (2; 4; 7)} болады.
Декарттық көбейтiндiлер үшiн мынадай қатыстар орын алады:
болса, ;
;
;
.
Математикада көптеген мәселелерді декарттық координаттар жүйесі арқылы шешеді. Түзудегі және жазықтықтағы нүктенің координаты ұғымын XVII ғасырда француз ғалымы және философы Рене Декарт геометрияға енгізді. Бұл оқиға математиканың жаңа дәуірі - функция ұғымы мен геометриялық түрлендірулердің пайда болуы және дамуы дәуірі болды. Рене Декарттың атымен жазықтықтағы тік бұрышты координаттар жүйесін атау келісілген және оны декарттық координаттар жүйесі деп атайды. Оны координат жазықтығы деп те атайды.
Координат жазықтықтығында М нүктесін салу үшін оның орыны абсцисса және ордината деп аталатын екі санмен анықталады. М нүктесінің абсциссасы - оның Ох осіндегі проекциясы М1 нүктесінің координаты х, ал ординатасы - Оу осіндегі проекциясы М2 нүктесінің координаты у болады. Сонымен М нүктесінің абсциссасы х, ординатасы у дегенді М(х,у) түрінде жазады.

№4Дәріс
Жоспар:
1. Сәйкестіктер. Сәйкестік ұғымы.
2. Сәйкестіктің берілу тәсілдері.
3. Сәйкестіктің графы.
4. Берілген сәйкестікке кері сәйкестік, оның графы мен графигі.
5. Өзара бірмәнді сәйкестіктер

Жиындар арасындағы сәйкестік деп жиындардың үштігі аталады: Х жиыны, У жиыны және G - жиыны, ал ол ХхУ декарттық көбейтіндісінің ішкі жиыны. Х-сәйкестіктің шығу жиыны, У-сәйкестіктің келу жиыны, G -сәйкестік графигі деп аталады. Мысалы, кесіндінің ұзындығын өлшеу барысында кесінді мен оның ұзындығын өрнектейтін нақты сандар арасында сәйкестік орнатуға болады.
Сәйкестік ұғымы түсініктірек болуы үшін мысал қарастырайық. Мысал: Х={3,5,7,9} және У={4,6} жиындары элементтерінің арасында R: артық деген қатыс берілсін. Осы қатыстың парларын жазайық: G={(5,4),(7,4),(9,4),(7,6),(9,6)}.
ХхУ декарттық көбейтіндісі: ХхУ={(3,4),(3,6),(5,4),(5,6),(7,4), (7.6),
(9,4),(9,6)} болып, ал G жиыны ХхУ парлары жиынының ішкі жиыны болғандықтан олар бір-бірімен R қатысымен байланысты екен.
Сәйкестіктің берілу тәсілдері
1. Егер X пен У шекті жиындар болса, онда осы жиындар арасындағы R қатысы, сол қатысқа тиісті барлық парларды атау арқылы беріледі.
2. X пен У жиындары арасындағы R қатысы, қатысқа тиісті барлық парлардың сипаттамалық қасиеттерімен беріледі. Мысалы, N сандар жиынында "х, у-тен үлкен", "х саны у санынан 2-ге артық" қатыстарын басқаша сипаттауға да болады. Немесе X жиынында "артық болу" қатысы берілсе, оны "2-ге артық болады" деп айтуға да болады.
3. Сандық жиындар элементтері арасындағы сәйкестік координат жазықтығында графикпен беріледі.
4. Сәйкестік екі айнымалысы бар теңдеулер арқылы беріледі.
5. Сәйкестік граф көмегімен де беріледі.
Кейбір сәйкестіктерді жазуға арнайы белгілер бар.
N-натурал сандар жиынындағы теңдікті "х=х", деп жазса, ал "х саны у санынан үлкен" сәйкестігін "ху" түрінде жазуға болады.
Егер Х={1,3,5,7}, У={2,4,6,8,10}, ал Х және У жиындары арасында Х жиынындағы х саны У жиынындағы у санынан үлкен R сәйкестігінің графигі G={(3,2),(5,2),(5,4),(7,2),(7,4),(7 ,6)} болса, онда, G жиынының (3,2) жұбы туралы 3ϵХ және 2ϵУ сандарының арасында R сәйкестігі орындалады деп немесе R сәйкестігі 2 саны 3 санына сәйкес келеді деп айтуға болады және оны былай жазады: 3R2. Сонда, 3R2 жазуы былай оқылады: Х жиынынан алынған 3 саны У жиынынан алынған 2 санынан үлкен.
Х={1,3,5,7} және У={2,4,6,8,10} жиындарының арасындағы х саны у санынан үлкен деген R сәйкестігін көрнекі Эйлер-Венн диаграммаларымен кескіндеу үшін, берілген жиындардың элементтерін нүктелер арқылы белгіленеді. Сонан соң сәйкестіктің графына тиісті әрбір (х,у) жұптарының элементтерін басы х элементін кескіндейтін нүктеде, ал соңы у элементін кескіндейтін нүктеде болатын стрелкамен қосады, ол R сәйкестігінің графы болады (19- сурет).

Графта (19-сурет) 7 санын өрнектейтін нүктеден үш стрелка шығатындығы көрініп тұр. Бұл Х={1,3,5,7} және У={2,4,6,8,10} жиындарының арасындағы х саны у санынан үлкен R сәйкестік үшін, 7ϵХ элементіне У жиынының үш элементі сәйкес келеді: 7R2, 7R4, 7R6 дегенді білдіреді.
3ϵХ элементіне У жиынының тек бір ғана элементі 2 сәйкес келеді. Графта 3 санын өрнектейтін нүктеден бір ғана стрелка шығады.
Ал 1ϵХ элементіне У жиынының бірде-бір элементі сәйкес келмейді, сондықтан да графта оны өрнектейтін нүктеден ешқандай стрелка шықпайды.
Егер Х және У жиындарының арасында қандайда бір R сәйкестік тағайындалған болса, онда Х шығу жиынының элементіне:
а) У келу жиынының бірнеше (тіпті шектеусіз көп) элементтерінің сәйкес келуі;
б) У жиынының тек бір ғана элементі сәйкес келуі;
в) У жиынының бірде-бір элементі сәйкес келмеуі мүмкін.
Керісінше айтсақ, келу У жиынының элементі шығу Х жиынының бірнеше элементтеріне, не тек бір элементіне сәйкес келуі, немесе бірде-бір элементіне сәйкес келмеуі мүмкін.
Жиындар арасындағы сәйкестік ұғымы математикадағы негізгі ұғымдарының қатарына жатады. Олай болатын себебі: бұл ұғым математикадағы функция және бейнелеу сияқты аса маңызды ұғымдарды анықтаудың негізі болып табылады.
23-суретте Х={1,2,3} және У={а,в,с} жиындарының арасындағы қайсыбір R сәйкестігінің графы берілген. Бұл жерде 1ϵХ элементіне У жиынының а және в элементтері сәйкес, яғни 1Rа, 1Rв, 2Rа, 2Rв, 2Rс екені көрінеді.

23-суреттегі граф арқылы аϵУ элементінің Х жиынының екі элементіне 1 және 2 сандарына сәйкес екендігі де анықталған. Басқаша айтқанда, аϵУ элементі бойынша керісінше а элементіне сәйкес келетін Х жиынының элементтерін табуға болады. Осы процесті жүзеге асыру үшін біз У жиынынан шығып Х жиынына келеміз (24-сурет). Мұндай жағдайда Х және У жиындарының арасындағы R сәйкестілігіне У және Х жиындарының арасында кері сәйкестік бар болады дейді. R сәйкестігіне кері сәйкестікті R-1 түрінде белгілейді (эрдің минус бір дәрежесі деп оқиды). R-1 сәйкестігінің графы R сәйкестігінің графындағы стрелкаларын кері бағыттаудан келіп шығады.
Х және У жиындары арасындағы R сәйкестігі графигі ХхУ декарттық көбейтіндінің ішкі жиыны болғандықтан, ХхУ декарттық көбейтіндісінің графигіне тән қасиеттерінің бәрі, R сәйкестігінің графигі үшін де тура болады. Демек декарттық көбейтінді сияқты Х және У жиындарының арасындағы R сәйкестігінің графигін де тік бұрышты координаталар жүйесінде нүктелер жиыны ретінде кескіндеуге болады екен.
R және R-1 сәйкестіктерін тік бұрышты координаталар системасында кескіндегенде олардың графиктері өзара қандай байланыста болатынын анықтайық. Ол үшін Х={-3,-2,-1,0} және У={0,1,-2} жиындарының арасындағы хϵХ саны уϵУ санынан кем деген R сәйкестік бар болсын. Сонда R сәйкестігінің графигі {(-3, 0), (-3, 1), (-3, -2), (-2,0), (-2,1), (-1,0), (-1,1), (0,1)} болады да, тік бұрышты координаталар жүйесінде 25-суретте көрсетілген сегіз нүкте болады.

Берілген сәйкестікке кері R[-1] сәйкестігінің графигі: {(0, -3), (1,-3), (-2, -3), (0, -2), (1, -2), (0, -1), (1,-1), (1, 0)} мынадай болады. Оның координаттық жазықтықтағы кескіні 26-суретте сегіз нүкте болып тұр.
R және R[-1] сәйкестіктері графиктерін бір суретке салайық (27-сурет). Енді R және R[-1]сәйкестіктерінің графиктері бірінші және үшінші координаталық бұрыштардың биссектрисасына қарағанда симметриялы екеніне оңай-ақ көз жеткізуге болады.
Мысалда У және Х жиындарының арасындағы R[-1] сәйкестік уϵУ саны хϵХ санынан үлкен деген сөйлеммен берілген.

Сонымен, егер Х және У жиындарының арасындағы сәйкестік R болса, онда У және Х жиындарының арасындағы уR[-1]х, уϵУ, хϵХ болатындай R[-1] сәйкестігі хRу болғанда және тек сонда ғана R сәйкестігіне кері сәйкестік болып табылады.
R және R-1 сәйкестерін өзара кері сәйкестер. Өзара кері сәйкестер графиктерінің ерекшеліктерін анықтау үшін R={(5,4),(7,4),(9,4),(7,6))} сәйкестігі графигін салғаннан кейін R-1={(4,5),(4,7),(4,9),(6,7)} сәйкестігінің графигін салған кезде әр пардың 1-ші компоненті У жиынынан, ал 2-ші компоненті X жиынынан алынады. Нәтижеде R және R-1 сәйкестер графиктері бірі-біріне симметриялы беттеседі. R және R-1 сәйкестері графиктерін бір-бірінен айыру үшін R-1 сәйкестігі парының 1-ші компонентін абцисса деп, ал 2-ші компонентін ордината деп есептеу келісілген.
Бастауыш математикасында өзара кері сәйкестерге ерекше көңіл бөлінеді. Оқушылар 53 болса, 35 болатынын жақсы түсінуі керек.
Кері сәйкестік ұғымы өмірде жиі пайдаланылады. Мысалы: Х - әр түрлі қазақ сөздерінің жиыны, ал У - қазақ тіліндегі сөз таптарының жиыны болсын. Осы жиындардың арасында х сөзі у сөз табына жатады деген сәйкестік бар (үй сөзі - зат есім, жаз сөзі -етістік т.с.с.). Осы сәйкестікке кері У және Х жиындарының арасындағы у сөз табына х сөзі жатады сәйкестігі (зат есімге үй сөзі, етістікке жаз сөзі жатады) түрінде айтылатын болады.
Егер Х - әлемдегі мемлекеттер жиыны, ал У - олардың астаналары жиыны болса, онда Х пен У-тің R сәйкестігі х мемлекетінің астанасы у болады. Онда У пен Х жиындары арасында R-1 сәйкестігі у қаласы - х мемлекетінің астанасы деп тұжырымдалады.
Х және У жиындары элементтерінің арасындағы барлық мүмкін болатын сәйкестіктердің ішінде бізді X жиынының әрбір элементіне У жиынының тек бір ғана элементі сәйкес келетін сәйкестікгер қызықтырады. Мұндай сәйкестіктерді өзара бірмәнді сәйкестіктер деп атайды. Осындай сәйкестіктердің мысалдарын қарастырайық.
1. А={а,b,с,d}, В={1,2,3,4} жиын элементтері арасындағы сәйкестік граф (74- сурет) арқылы көрсетілген.

А жиынының әрбір элементіне В жиынының бір ғана элементі сәйкес қойылғандықтан және В жиынының әрбір элементіне А жиынының тек бір ғана элементін сәйкес қоюға болатындықтан берілген сәйкестік А және В жиындарының арасындағы өзара бір мәнді сәйкестік болады: а-- 1; b--2; с--3; d--4.
2. X- координаттық түзудің нүктелерінің жиыны, ал У=R-нақты сандар жиыны болса, координаттық түзудің әрбір нүктесіне тек бір ғана нақты сан сәйкес келеіп, әрбір нақты санға бір ғана координаттық нүкте сәйкес қойылады.
3. Х- координаттық түзудің әрбір нүктесіне тек бір ғана нақты сан сәйкес келіп, әрбір нақты санға координаттық түзудің бір ғана нүктесі сәйкес қойылады. Сондықтан бұл сәйкестік өзара бірмәнді сәйкестік болады.
Егер жазықтықтың әрбір нүктесіне бір ғана нақты сандардың пары сәйкес келсежәне әрбір пар санға кординат жазықтығының бір ғана нүктесі сәйкес келсе, онда бұл сәйкестік өзара бір мәнді сәйкестік болады.
Өзара бірмәнді сәйкестік рефлексивті, симметриялық және транзитивтік қасиеттерге ие болады.
Өзара бір мәнді сәйкестік ұғымы бастауыш сыныпта айқын түрде қолданылмайды, бірақ санау және сандарды салыстыру барысында өзара бірмәнді сәйкестік қолданылады. Мысалы, 3=3 теңдігін түсіндіру үшін, үш қызыл дөңгелек пен үш жасыл шаршыны алып, олар бір-біріне сәйкестендіріледі.

№5 Дәріс
Жоспар:
Жиын элементтері арасындағы қатыстар.
Қатыстың негізгі қасиеттері.
Эквивалетті және реттік қатыстар
Екі жиын элементтерінің арасындағы сәйкестікті қарастырдық. Тек бір ғана жиын элементтерінің арасында әртүрлі байланыстар мен сәйкестіктер де болады. X=Y, арасында болатын дербес жағдайлар Х пен Х арасындағы бинарлық сәйкестік болып шығады, ол Х жиынындағы бинарлық қатыс деп аталады.
Егер ХХ декарттық көбейтіндінің ішкі жиыны көрсетілсе, онда Х жиынында қатыс берілген деп есептеледі. Қатысты сәйкестік сияқты P, R, S, Q т.б. әріптерімен белгілеу және хРу, хRy, хSу т.с. с. түрінде жазу қабылданған.
Анықтама. Жиындардардың (Х, Z) жұбын Х жиынындағы R бинарлық қатысы дейді. Мұндағы ZХХ, Х жиынындағы R қатыстың графигі болып табылады.
Шекті Х жиынында қатысты ерекше сызбаның көмегімен көрнекі түрде көрсетуге болады. Онда жиынның элементтерін нүктелермен белгілеп, содан соң (х,у) жұбы үшін хRу орындалатындай етіп х нүктесінен у нүктесіне бағытталған сызықтар жүргізіледі. Алынған сызба R қатысының графы деп аталады. Басталуы мен аяқталуы дәл келетін бағытталған сызықтар тұзақ деп аталады.
Мысал: Х={2, 4, 6, 8, 12} жиынында х саны у санының бөлгіші деген қатыстың графы 14-суреттегідей болады.

14-сурет
Қатыстың берілуі тәсілдері жиынның берілу тәсілдерімен өте ұқсас. Мысалы: Х жиынындағы R қатысты осы қатыспен байланысты болатын Х жиынынан алынған элементтердің барлық жұптарын атау арқылы анықтап беруге болады.
Қатыстың берілуі тәсілдерін жазу әр түрлі болуы мүмкін: жұптар жиыны жазылады, қатыстың графы немесе графигі сызылады, кесте беріледі, т.с.с.
Көбінесе Х жиындағы R қатысты осы қатыста болатын барлық элементтердің сипаттамалық қасиеттерін көрсету арқылы анықтап береді. Сонда бұл қасиет екі айнымалылы сөйлем, яғни теңдеу немесе теңсіздік түрінде тұжырымдалады.
Математикада екі объектінің арасында болатын әр түрлі қатыстар қарастырылады. Олардың әрбіреуі қандай да бір Х жиынында қарастырылатын жұптардың жиыны болып табылады. Егер X жиынының кейбір элементтері У жиынының кейбір элементтерімен берілген қатыста болса, ол бинарлық қатыс (сәйкесітік) деп аталады. Оларды қатыстың кейбір қасиетін негізге ала отырып классификациялауға болады. Сол жағдайда қолданылатын қатыстың негізгі қасиеттерін қарастырайық.
1. Егер әрбір х элементі өзімен өзі R қатыста бола алса, онда Х жиынындағы R қатысы рефлексивті деп аталады, яғни егер Х жиынындағы кез келген х үшін хRх ақиқат болса, онда R қатысы рефлексивті. Мысалы, а=а теңдік қатысы.
2. Егер Х жиынының бір де бір элементі өзімен өзі R қатыста бола алмаса, онда R қатысы антирефлексивті деп аталады. Мысалы, аb перпендикулярлық қатыс.
3. Егер Х жиынының кез келген х және у элементтері үшін хRу болатындығынан уRх болатыны шығатын болса, онда R қатысы симметриялы деп аталады Мысалы, аb параллельдік қатыс.
4. Егер Х жиынының ешбір х және у элементтері үшін бір мезгілде хRу және уRх бола алмаса, онда R қатысы антисимметриялы деп аталады. Мысалы, нақты сандар жиынында берілген ав кіші болу қатысы.
5. Егер х=у болғанда, сонда және тек сонда ғана бір мезгілде хRу және уRх бола алса, онда R қатысы асимметриялы деп аталады. Мысалы, нақты сандар жиынында берілген ав кіші немесе тең болу қатысы. Шындығында антисимметриялы және асимметриялы қатыстардың теңәлділігін дәлелдеуге болады.
6. Егер Х жиынының кез келген х, у, z элементтері үшін хRу және уRz болатындығынан хRz болатыны шығатын болса, онда R қатысы транзитивті деп аталады. Мысалы, кесінділер жиынында берілген х кесіндісі у кесіндісінен ұзын және у кесіндісі z кесіндісінен ұзын болуынан х кесіндісі z кесіндісінен ұзын болуы қатысы.
7. Егер Х жиынының кез келген әртүрлі екі элементінің әйтеуір біреуі екіншісімен R қатыста бола алса, онда Х жиынындағы R қатысы байламды деп аталады. Мысалы, {1, 3, 5, 6} жиынында кіші болу қатынасы байламды, ал бөлгіші болу қатынасы осы жиында байламды емес.
Қатынастың бұл қасиеттері, оларды графтар арқылы кескіндеу барысында көрнекі бейнеленеді. Мысалы: егер Х жиынындағы R қатынасы рефлексивті болса, онда бұл қатынастың графының әр төбесінде тұзақ болады; егер R қатынасы симметриялы болса, онда графта х нүктесімен у нүктесін қосатын қарама-қарсы бағытталған сызықтар болуы керек; транзитивті қатыныстың графында х нүктесінен у нүктесіне және у нүктесінен z нүктесіне жүргізілген бағытталған сызықтармен қатар х нүктесінен z нүктесіне жүргізілген бағытталған сызық та болуы керек.
Анықтама. Қандайда рефлексивті, симметриялы және транзитивті қатыстары жиынында орындалса, онда ол эквивалентті қатыс деп аталады.
Мысалы, "Ағаштар" жиынында берiлген х ағашының биiктiгi мен у ағашының биiктiгi бiрдей қатысының қасиеттерiн анықтаңыз.
Шешуi. Ағаштар жиынында "биiктiктерi бiрдей" қатыс рефлексивтi, симметрялы және транзитивтi қасиеттерiне ие болады. Олардың рефлексивтi қатынаста болатыны әрбiр ағаштың биiктiгi өзiне-өзi тең екенін білдіреді.
Ал, егер х ағашының биiктiгi у ағашының биiктiгiне тең болса, онда у ағашының биiктiгi х ағашының биiктiгiне тең болып симметриялық қасиетке ие болады.
Соңында, егер х ағашының биiктiгi у ағашының биiктiгiне және у ағашының биiктiгi z ағашының биiктiгiне тең болса, онда х ағашының биiктiгi z ағашының биiктiгiне тең болады. Яғни, транзитивтiк қасиет орын алады.
Сондықтан, "Ағаштар" жиынындағы "биiктiктерi бiрдей" қатысы эквиваленттi болады.
Кезкелген эквивалентті қатыс Х жиынын эквивалентті кластарға жіктейді. Жалпы жағыдайда Х жиынын өзара қос-қостан эквивалентті кластарға жіктеу элементінің саны ұғымына алып келеді. А шектеулі жиын болса, оған эквивалентті В жиыны да шектеулі болады деп қорытындылау Георог Кантор енгізген жиынның қуаты ұғымына негіз болды.
Анықтама. А және В жиындары эквивалентті болғанда тек сонда ғана тең қуатты болады.
А жиынның қуатын n(A) деп белгілеп, жоғарыдағы анықтаманы n(A) = n(B) деп тұжырымдап, A ~ B түрінде жазамыз.
Анықтама. Қандайда антирефлексивті, антисимметриялы және транзитивті қатыстары жиынында орындалса, онда ол реттік қатыс деп аталады.
Мысалы, "Ағаштар" жиынында берiлген х ағашы у ағашынан қысқа қатысының қасиеттерiн анықтаңыз.
Шешуi Ағаштар" жиынындағы "биiктiгi қысқа" қатыс төмендегi қасиеттерге ие болады.
1. Антирефлексивтi қасиетке ие, өйткенi әрбiр ағашты өзiнен-өзi қысқа деуге болмайды.
2. Асиметриялы қасиетке ие. Өйткенi, егер х ағашы у ағашынан қысқа болса, онда бұдан у ағашы х ағашынан қысқа деуге болмайды.
3. Транзитивтi қасиет орын алады. Себебi, егер х ағашы у ағашынан және у ағашы z ағашынан қысқа болса, онда х ағашы z ағашынан қысқа болады.
Жоғарыда көрсетiлген үш қасиетке ие болатын "Ағаштар" жиынындағы "биiктiгi қысқа" қатысы қатаң реттiк қатыс болады.
№6 Дәріс
Жоспар:
Математикалық логика элементтері. Пiкiр ұғымы.
Логикалық операциялар және олардың заңдары

Логика деген не? LOGOS (грек сөзі)- ұғым, түсінік, пікір айту, ақыл дегенді білдіреді Логика - ойлау процессі бағынатын ережелер жиынтығы.
Абстракты ойлаудың негізгі формалары: түсінік (ұғым), талдау (талқылау), ақыл-ой қорытындылау.
Түсінік (ұғым ) - бір заттың немесе біртектес заттардың негізгі белгілерін көрсететін ойлау формасы ( Мысалы: трапеция, үй).
Талдау - зат туралы кейбір ойды құптау немесе жоққа шығару (көкткм шықты, және құстар ұшып келді).
Ақыл-ой қорытындылау - берілген білімнен жаңа білім шығарып алудың ойлау тәсілі (барлық металдар - қарапайым заттар).
Формальды логика - дұрыс ойлаудың заңдары мен формалары туралы ғылым.
Математикалық логика - логическалық байланыстар мен қатыстарға негіз болатын логикалық (дедуктивтік) тұжырымдарды зерттейді. Логиканың даму кезеңдері:
АРИСТОТЕЛЬ (б.э.д. 384-322жж.) - логиканың негізін қалаушы. Кітаптары:
КАТЕГОРИЯЛАР;
БІРІНШІ АНАЛИТИКА;
ЕКІНШІ АНАЛИТИКА.
Ол талқылаудың әртүрлі формаларын зерттеген. Талқылау, силлогизм ұғымын енгізген. Силлогизм - берілген екі пікірден ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.