10-11 сынып оқушыларына стереометрияның қиындатылған есептерін оқыту әдістемесінің ғылыми негіздері


КІРІСПЕ
Еліміздің әлеуметтік-экономикалық дамуын жақсарту қоғамдық өмірдің барлық саласында түбегейлі терең өзгерістер жасауды, ең алдымен, адам санасын шыңдауды, жаңаша ойлар қалыптастыруды, халқының өткен тарихи-мәдени мұраларын игере отырып шығармашылықпен еңбек етуді талап етеді. Қазақстанның ХХІ ғасырда өркениетті әлемнен орын алып, дамыған елдер деңгейіне жетуіне ықпал етер бірден-бір құдірет - білім және білімді ұрпақ. Білім беру жүйесінің барлық буындарына, соның ішінде білім мен тәлім - тәрбиенің негізі бастауыш мектепте қаланса, жалғасын 5-11 сыныпта табады.
Тәуелсіздік және егемендік алуына байланысты, өскелең ұрпаққа білім мен тәрбие беру мәселесін қоғам дамуына қазіргі кезеңнің талаптарынан туындап отырған міндет және мақсаттарға орай жан-жақты жетілдіру қажет болып отыр.
Мектепте оқылатын пәндерден жаңа мемлекеттік стандарт, бағдарламалар жасалып, соларға сәйкес төлтума оқу-әдістемелік жиынтықтар жазылады, демек, оқу-тәрбие процесін ұйымдастырудың жаңа жүйесі мектептердің тәжірибесіне енгізілуде, яғни педагогикалық ғылымның озық идеяларымен жинақталған құнды тәжірибелердің нәтижелері өзгерген және жаңа жағдайларда өзінің қолданысын табуда.
Осындай күрделі мәселенің дұрыс шешілуі ұстаздардың теориялық білімінің және кәсіби мамандығының деңгейіне тәуелді. Сондықтан, оқушыларына тек қана білім берумен шектеліп қалмай, қазіргі заман талабына сай тәлім-тәрбие беретін, яғни халқымыздың тарихы, мәдениеті, салт-санасы, әдеп-ғұрпы, педагогикасымен таныстырып, ой-өрісін, қабілетін жан-жақты дамытуға толық мүмкіндік туғызады.
Еліміз егеменді мемлекет болғалы бері барлық салаларда өзгерістер жүргізіп жатыр. Мұндай өзгерістерден білім беру сапасын да тыс қалған жоқ. Қазіргі білім беру жүйесі әлемдік өркениеттің барлық талабына сай келетін парасатты білім мен біліктілігі жетілген мамандар дайындауды қажет етеді. Сондықтан да Қазақстан Республикасының «Білім туралы» заңында білім беру жүйесінің міндеті ұлттық және жалпы азаматтық құндылықтар, ғылым мен практика жетістіктері негізінде жеке адамды қалыптастыруға, дамытуға және кәсіби шыңдауға бағытталған білім алу үшін қажетті жағдай жасау екендігі айтылған.
Бұл саладағы еңбектерді, әдебиеттерді талдау - осы бағыттағы зерттеулерді әрмен қарай жан-жақты жалғастыру қажет екенін көрсетеді.
Бұл біздің зерттеу жұмыстарымыздың көкейкестігін көрсетеді.
10-11 сынып оқушыларына стеометрияның қиындатылған есептерін шешудің әдістерін білу, оны сабақта қолдану мәселесі - біздің зерттеу проблемамыз болып табылады.
Зерттеу мақсаты - орта мектептің 10-11 сынып математика курсында стеометриялық элементтерді оқытуда білім беру үрдісінің стеометрияның қиындатылған есептерін шешудің әдістерін білу және оның тиімділігін арттыру, соның негізінде оның әдістемесін жасау.
Зерттеу нысаны - математика курсында стеометрияның қиындатылған есептерін шешудің әдістерін білу және оқыту үрдісі.
Зерттеу пәні - стеометрияның қиындатылған есептерін шешудің әдістерін білу және оқыту үрдісінде әдістемелік нұсқаулықты қолдану.
Зерттеудің ғылыми болжамы - егер 10-11 сынып математика курсында стеометрияның қиындатылған есептерін шешудің әдістемесі жасалып, ол оқу үрдісіне енгізілсе, онда оқушылардың геометриядан алған білімдерінің сапасы артады, өйткені бұл жағдайда стереометрияның қиындатылған есептерін шешудің әдістемесі стереометриялық материалдарды меңгеру барысы арттады, стеометриялық элементтерінің арасындағы байланыстарды дәл анықтауға және де математикалық ұғымдарды қалыптастырудың тиімділігінің артуына, оқушыларда есептер шығару іскерліктері жоғары дәрежеде қалыптасуына жағдай жасалады.
Қойылған зерттеу мақсатына сәйкес, зерттеу болжамын тексеру үшін, зерттеу жұмысының мынандай міндеттерін шешу қажет болды:
- 10-11 сынып оқушыларының психологиялық-педагогикалық ерекшеліктерін қадағалау;
- 10-11 сынып оқушыларының геометриялық түсініктерін қалыптастырудың жолдарын жасау;
- 10-11 сынып математикасындағы геометриялық элементтерді түсіндіру;
- 10-11 сынып оқушыларына геометриялық түсініктерді дамытуды тәрбиелік - эксперименттік жолмен түсіндіру, әдістемелік нұсқаулар беру;
- 10-11 сынып оқушыларына геометриялық фигураларды оқытуда дидактикалық мүмкіншіліктерін зерттеу.
Жетекші идея : 10-11 сынып оқушыларының геометриядан алатын білім сапасын арттыруға, жалпы оқу іскерліктері мен дағдыларын қалыптастыруға, оқушылардың кеңістікті елестету қабілетін арттыруға, есептерді шығара білу, өзін-өзі бақылау, бағалау іскерліктерін қалыптастыруға, өздігінен танымдық белсенділіктерін арттыру болып табылады.
Зерттеудің әдіснамалық негіздері : таным, білім, жеке тұлға және оның іс-әрекеті, ақыл-ой, ойлау, құндылық туралы философиялық, психологиялық, педагогикалық теориялар мен тұжырымдамалар, білім сапасын арттыру туралы қағидалар болып табылады.
Зерттеу әдістері : оқушылардың психологиялық-педагогикалық жас ерекшеліктерін зерттеу; геометрия пәні бойынша жасалған оқу бағдарламаларына, оқулықтарға, есептер жинақтарына, әдістемелік құралдарға, ғылыми-әдістемелік негізде талдау жасау; оқушылардың математикалық білім, білік және дағдыларының жайын зерттеу; пән мұғалімдерімен әңгімелесу; тәжірибелік-эксперимент жүргізу; сауалнамалар жүргізу; эксперимент нәтижелерін математикалық статистика көмегімен өңдеу және қорытындылау.
Диссертациялық жұмыстың құрлымы: жұмыс кіріспеден, екі бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен және қосымшалардан тұрады.
1. МЕКТЕПТЕ ГЕОМЕТРИЯНЫ ОҚЫТУДЫҢ ҒЫЛЫМИ НЕГІЗДЕРІ
- Мектепте геометрияны оқыту
Жалпы білім беретін орта мектепте оқытылатын пәндер ішінен геометрия пәнінің орны ерекше. Ол математикалық пәндер тобында оқушылардың білімін тексеретін, бағалайтын, сараптайтын іс-әрекеттердің бәріне қатысады.
Геометрия (көне грекше:γεωμετρία көне грекше: γή -жер және көне грекше: μετρίω - «өлшеу») -математиканың кеңістіктік пішіндер (формалар) мен қатынастарды, сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін ғылым саласы. Бұл анықтаманың соңғы жағы, атап айтқанда, « . . . сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды . . . » деген бөлігі ұғым анықтамасына кейін қосылған тіркес. Бұл тіркес қайдан және неге шықты?
Математиктер геометрияның даму таризын бес кезеңге бөліп қарастырады.
1-кезең. Ерте заманнан біздің заманымыздың 5 ғасырға дейінгі аралықты қамтиды.
Геометрия дамуының бұл кезеңінде қарапайым геометриялық ұғымдар Мысыр мен Вавилонда, Грекияда, Үндістанда, Қытайда пайда бола бастады. Оларға мыналар жатады: жер өлшеу, геометриялық мәліметтерді астрономияда қолдану, ұзындықтар мен бұрыштарды өлшеу, қарапайым фигуралардың (квадрат, қиық пирамида) ауданы мен көлемін есептеу, дұрыс көпбұрыштардың, қиық конустың ауданын табу, шеңберді 360 градусқа бөлу, есептерді теңдеулерге келтіру, Пифагор теоремасы және т. б.
Қарастырылып отырған кезеңнің соңына қарай Грекияда ғылыммен арнаулы айналысатын оқымыстылар шықты. Олар, тек қана бар мәліметтерді жүйелеп қана қоймай геометриялық тұжырымдарды, сөйлемдерді немесе математикалық тілмен айтқанда теоремаларды дәлелдеуге тырысты.
Бұл кезеңде геометрияның дамуына Фалес, Пифагор, Гиппократ, Демокрит, Феодесий сияқты грек ғалымдары зор үлес қосты. Олар геометрияны кезең соңына қарай ғылым дәрежесіне көтерді. Осы кезеңнің аяғында Гиппократ, Феодесий «Геометрия негіздері» деген атпен көлемді кітаптар жазды.
2-кезең. Евклидтен Р. Декартқа дейінгі, шамамен екі мың жылға созылған аралықты қамтиды.
Геометрия дамуының бұл кезеңінде геометрия саласындағы ең елеулі жұмыс-ол грек ғалымы Евклидтің өзіне дейінгі математикалық білімдер жүйелеп, жинап, талдап, қорытып, бір ізге түсіріп, біздің заманымыздан бұрын 300 жылы шамасында «Негіздер» ( Кейбір еңбектерде «Бастамалар» деп те атайды) атты, 13 бөлімнен, онда 121 анықтама, 5 постулат, 9 аксиома, 373 теорема келтірілген шығарма жазуы дер едік . . . Аксиоматикалық жолмен құрылған бұл, Евклид геометриясы әлі күнге дейін жалпы білім беретін мектептерде оқытылып келеді.
Сол сияқты бұл кезеңде геометрияның дамуына Архимед (дөңгелектің, парабола сегментінің ауданы, пирамиданың, конустың және шардың көлемі жөніндегі теоремалар), Апполлоний (конустық қималар), Гиппарх, К. Птолемей, Менелай (сфералық геометрия, тригонометрия) үлкен үлес қосты. Жалпы Грекиялық жоғарғы ғалымдардың еңбек істеген уақыттарын грек геометриясының «алтын ғасыры» деп бағалайды.
Орта Азия мен Қазақстан оқымыстыларынан бұл кезеңде геометриямен шұғылданғандар: Ғаббас әл-Жауhари, Әбу Наср әл-Фараби, Әбу Райхан әл-Бируни, Ғийас әд-Дин Жәмшид әл-Кәши болды.
Екінші кезең соңына қарай геометрия Батыс Еуропада жандана бастады. Бұл кезеңде И. Кеплер мен итальян математигі Б. Кавальеридің еңбектері өмірге келді.
Евклид постулаттары
Евклид (шамамен б. д. д 325 жыл - шамамен б. д. д 256 жыл)
Бірінші постулат: Екі нүкте арқылы тек қана бір түзу жүргізуге болады.
Екінші постулат: Кесінді шексіз жалғаса береді.
Үшінші постулат: Кез келген нүктеден кез келген радиустағы шеңбер сызуға болады.
Төртінші постулат: Барлық тік бұрыштар өзара тең.
Бесінші постулат:Түзуден тыс жатқан нүктеден түзуге параллель бір ғана түзу жүргізуге болады.
3-кезең . Р. Декарттан Н. И. Лобачевскийге дейінгі шамамен 200 жылға созылған аралықты қамтиды.
Геометрия дамуының бұл кезеңіне тән жағдайлар.
Бұл кезеңде геометрияның дамуына француз және неміс математиктері ерекше күш шығарды. Осы уақыт аралығында:
- Координаттар әдісіне сүйенген, негізін француз математиктері Р. Декарт пен П. Ферма қалаған аналитиклық геометрия;
- Негізін француз математиктері Ж. Дезарг, Б. Паскаль, Ж. Понселе, неміс математигі К. Штадут, швейцар математигі Я. Штейнер қалаған проективтік геометрия;
- Негізін француз математигі Г. Монж қалаған сызба геометриясы (Бұл геометрия бір жағынан проективтік геометрияның бір бөлімі болып та есептелінді) ;
- Негізін неміс математигі Эйлер мен француз математигі Г. Монж қалаған дифференциалдық геометриялар өмірге келді.
4-кезең. Лобачевский еңбектерінен басталады.
Геометрия дамуының бұл кезеңіне тән жағдайлар:
Орыс ғалымы Лобачевский 1829 жылы Евклидтің бесінші постулатын қарсы жору арқылы, яғни «Түзуден тысқары жатқан нүкте арқылы түзуге кем дегенде екі параллель түзу жүргізуге болады» деген тұжырымды дәлелдеу барысында ешбір қарама-қайшылыққа кездескен жоқ. Осы жағдайдың негізінде үш түрлі пайымдау жасады.
- Евклид геометриясы болуға тиіс және ол бірден-бір геометрия емес;
- Аксиомаларды өзгертіп, жаңа геометрия жасауға болады;
- Нақты кеңістікке қандай геометрия сәйкес келетіндігін тәжірибе көрсетеді.
Бұл шын мәнінде геометрия тарихындағы революция еді. Демек, екі мың жыл бойы «Евклидтік геометриядан басқа геометрия жоқ» делінген қағида бұзылды. Бұл жағдайлар неміс математигі Гаусс пен венгр математигі Я. Больяйда жақын келді.
Осы кезеңде, бесінші постулат орнына өз аксиомасын ұсынған неміс математигі Ф. Б. Риман, Риман геометриясының немесе эллипстік геометрияның негізін қалады.
Лобачевский геометриясы немесе Гиперболалық геометрияда:
- Түзуден тысқары жатқан нүкте арқылы түзуге өте көп параллель түзу жүргізуге болады.
- «Үшбұрыштардың ішкі бұрыштарының қосындысы 180 градустан кем»
- Пифагор теоремасы орындалмайды және т. б.
- Риман геометриясы немесе эллипстік геометрияда (Бұл геометрияны, сфералық геометрия, жер беті геометриясы, аспан денелері геометриясы деп те атайды) :
- Түзуден тысқары жатқан нүкте арқылы түзуге параллель түзу жүргізуге болмайды.
- «Үшбұрыштардың ішкі бұрыштарының қосындысы 180 градустан артық»
Лобачевский және Риман геометриялары Евклид геометриясын теріске шығармайды. Бірақ, олар белгілі бір кеңістіктерде ғана орындалады, ол барлық кеңістіктер үшін әмбебап геометрия емес. Сол үшін олар жекелеген кеңістіктер үшін Евклид геометриясынан басқа да геометриялар бар деп тұжырымдайды. Лобачевчкий идеялары геометрияның жалпылануына және олардың одан әрі дамуына кең жол ашты. Соның негізінде, геометрия тағы да сараланып, топология, көп өлшемді кеңістіктер геометриясы, көпбейнеліктер геометриясы және тағы басқа салаларға бөлінді.
5-кезең. Қазіргі геометрия
Қазіргі геометрияға тән жағдайлар: кеңістік пен фигураны жиын ұғымы арқылы анықтайды. Ол, табиғатты зерттеуде, техниканы дамытуда қуатты құрал болып табылады. Ол математикалық анализге, механикаға, физикаға, астрономияға, геодезияға, картографияға, кристаллографияға, тағы басқа ғылымдардың дамуына айтарлықтай ықпал етуде.
Қазіргі Геометрия, кеңістік пен фигураны жиын ұғымы арқылы анықтайды. Ондағы кеңістік әдеттегі қатынастар сияқты анықталған элементтердің жиыны ретінде қарастырылады. Табиғатты зерттеуде, техниканы дамытуда маңызды құрал- геометрия. Геометрия түрлі ғылымдарға маңызды ықпал етеді: математикалық анализ, механика, физикa, астрономия, геодезияға, кристаллография, картография, және тағы басқа.
Мектеп геометрия курсын құру туралы әр түрлі пікірлер бар және оларға сәйкес оқулықтар да жазылуда, бірақ ешқандай ортақ келісімге келген жоқ. Біреулерді геометрияны алгебраландыруды, яғни координаталық әдісті кең түрде қолдануды ұсынады. Екінші біреулері геометрия курсын геометриялық түрлендірулер идеясы негізінде құруды, ал үшіншісі геометриялық ұғымдарды вектор негізінде түсіндіруді жақтайды. Дедуктивті-аксиоматикалық жүйеде және жоғары логикалық деңгейде құрылған геометрия курсының 2000 жылдан артық үлгісі болып келген Евклидтік геометриядан мектепте, әсіресе мектептің жоғары сыныптарында тіптен бас тартуға шақырып жататындар да бар.
Осындай жағдайда Евклидтің «Бастамаларының» негізін сақтап (А. П. Киселевтың оқулығы), оны жетілдірген А. В. Погорелов және Л. С. Атанасян және т. б. қаламдастығымен жазылған оқулықтарды басшылыққа алып жарық көрген төл оқулықтарымыз Евклидтік геометрияны - геометриялық білімдердің алғашқы қалыптасу көзі және даму болашағаның бастауы ретінде алған. Бұл білімдердің шындық дүниенің кеңістіктік қасиеттерін дұрыс бейнелейтіндігі және оны зерттеп-білудегі қажеттілігі адамзаттың мыңдаған жылдар бойы практикалық қызметі нәтижесінде дәлелденген.
Евклидтің «Бастамалары» негізінде оқушылардың алған ғылыми білімдері кеңістікті дұрыс есептеуге, кеңістік пен уақыттың өзара байланысын терең түсінуге, интелектуалдық қабілеттерін дамытуға игі әсерін тигізіп отырды. Осы білімдер негізінде Циолковский ғарышта ұшуды есептеді, ал Лобачевский шындық кеңістіктің жаңа моделін жасады, соның негізінде Эйнштейн өзінің салыстырмалы теориясын ашты т. с. с [6] .
Қазіргі мектеп геометрия курсы үшбұрыштардың теңдік және ұқсастық белгілер әдісі, тригонометриялық және алгебралық әдістер сияқты дәстүрлі әдістерді қолданумен бірге, аксиоматикалық әдісті, геометриялық түрлендірулер әдісін, координаталық және векторлық әдісті, математикалық талдау әдісінің элементтерін де пайдаланады.
1. 2 Жоғарғы сыныптарда стереометрияны оқыту
Стереометрияның жүйелі курсы планиметрия курсы құрылған схема бойынша құрылады:
Анықтама берілмейтін негізгі ұғымдар айтылады.
Негізгі ұғымдардың қасиеттері айтылған аксиомалар тұжырымдалады.
Негізгі ұғымдардың көмегімен басқа геометриялық ұғымдардың анықтамалары тұжырымдалады.
Анықтамалар мен аксиомалар негізінде теоремалар дәлелденеді.
Стереометрияда негізгі ұғым төртеу: нүкте, түзу, жазықтық және қашықтық. «Жиын» ұғымы да негізгі ұғым болып табылады, ол тек геометрияда ғана емес, математиканың барлық басқа бөлімдерінде де солай.
Геометрияда қандай да болмасын нүктелер жиынын фигура деп атайды. Фигураның қарапайым мысалы - түзу мен жазықтық.
Жазықтықты параллелограмм немесе қандай да бір жазық фигура түрінде кескіндейміз (1, 2-сурет) . Жазықтықты әдетте гректің
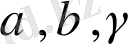 т. с. с. әріптерімен белгілейді. Ал нүктелер мен түзулер үшін планиметриядағы белгілеулерді сақтап қаламыз:
т. с. с. әріптерімен белгілейді. Ал нүктелер мен түзулер үшін планиметриядағы белгілеулерді сақтап қаламыз:
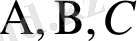 . . . нүктелері,
. . . нүктелері,
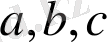 . . . , сондай-ақ (АВ), (АС) т. с. с. түзулері.
. . . , сондай-ақ (АВ), (АС) т. с. с. түзулері.
Егер А нүктесі
 жазықтығына тиісті
жазықтығына тиісті
 болса, онда:
болса, онда:
«
 жазықтығы А нүктесі арқылы өтеді (немесе жүргізілген) » деп айтылады (1-сурет) . А нүктесі тиісті болатын
жазықтығы А нүктесі арқылы өтеді (немесе жүргізілген) » деп айтылады (1-сурет) . А нүктесі тиісті болатын
 түзуіне қатысты да сондай терминдер қолданылады.
түзуіне қатысты да сондай терминдер қолданылады.
Стереометрияда қарастырылатын барлық нүктелердің жиыны кеңістік деп аталады.
. А
1-сурет 2-сурет
2. Стереометрия аксиомаларында анықталмайтын ұғымдардың: нүкте, түзу, жазықтық пен ара қашықтықтың негізгі қасиеттері өрнектелген. Стереометрия аксиомалары кеңістік қасиеттерін өрнектейді.
А к с и о м а-1: Кемінде бір түзу және кемінде бір жазықтық болады. Әрбір түзу және әрбір жазықтық дәлме-дәл келмейтін бос емес нүктелер жиыны болады.
1-аксиомадан кез келген
 жазықтығы үшін тиісті емес
жазықтығы үшін тиісті емес
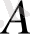 нүктесі болатындығы шығады (3-сурет) . Мұндай жағдайда
нүктесі болатындығы шығады (3-сурет) . Мұндай жағдайда
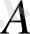 нүктесі
нүктесі
 жазықтығынан тыс алынған дейді де, былай жазады:
жазықтығынан тыс алынған дейді де, былай жазады:
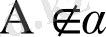 .
.
.

3-сурет
А к с и о м а-2. Кез келген әр түрлі екі нүкте арқылы бір, тек бір ғана түзу өтеді.
А к с и о м а-3. Жазықтықтың әр түрлі екі нүктесі арқылы өтетін түзу сол жазықтықта жатады.
«
 түзуі
түзуі
 жазықтығында жатыр» дегенді, басқаша айтқанда, «
жазықтығында жатыр» дегенді, басқаша айтқанда, «
 жазықтығы
жазықтығы
 түзуі арқылы өтеді» дегенді
түзуі арқылы өтеді» дегенді
 деп белгілейді.
деп белгілейді.
(3-сурет)
В



a
147-сурет
4-сурет
Егер түзу мен жазықтықтың ортақ бір нүктесі болса, онда түзу жазықты осы нүктеде қияды дейді. (4-сурет)
А к с и о м а-4. Бір түзуге тиісті емес үш нүкте арқылы бір, тек бір ғана жазықтық өтеді.
Бір түзуге тиісті емес
 ,
,
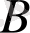 ,
,
 нүктелері арқылы өтетін
нүктелері арқылы өтетін
 жазықтығын (
жазықтығын (
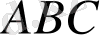 ) түрінде де белгілейді (5-сурет)
) түрінде де белгілейді (5-сурет)
M
a
. А . В
. С
рп
5-сурет
6-сурет
А к с и о м а-5. Егер әр түрлі екі жазықтықтың ортақ нүктесі болса, онда олардың қиылысуы түзу болады.
Қиылысуы түзу болатын екі жазықтық
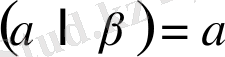 (6-сурет)
қиылысатын жазықтықтар
деп аталады.
(6-сурет)
қиылысатын жазықтықтар
деп аталады.
А к с и о м а-6. Кез келген
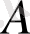 және
және
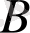 екі нүкте үшін
екі нүкте үшін
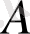 -дан
-дан
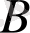 -ге дейінгі қашықтық деп аталатын теріс емес шама болады.
-ге дейінгі қашықтық деп аталатын теріс емес шама болады.
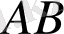 қашықтығы тек
қашықтығы тек
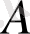 және
және
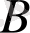 нүктелері дәл келіп беттескен жағдайда ғана нольге тең болады.
нүктелері дәл келіп беттескен жағдайда ғана нольге тең болады.
А к с и о м а-7.
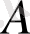 нүктесінен
нүктесінен
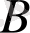 нүктесіне дейінгі қашықтық
нүктесіне дейінгі қашықтық
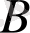 нүктесінен
нүктесінен
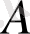 нүктесіне дейінгі қашықтыққа тең болады.
нүктесіне дейінгі қашықтыққа тең болады.
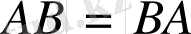
А к с и о м а-8. Кез келген
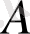 ,
,
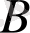 ,
,
 , үш нүкте үшін
, үш нүкте үшін
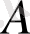 -дан
-дан
 -ге дейінгі қашықтық
-ге дейінгі қашықтық
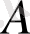 -дан
-дан
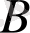 -ге және
-ге және
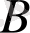 -ден
-ден
 -ге дейінгі қашықтықтардың қосындысынан артық емес.
-ге дейінгі қашықтықтардың қосындысынан артық емес.
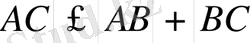
А к с и о м а-9. Әр жазықтық үшін планиметриядан белгілі реттік, жазықтықтың қозғалғыштығы және параллель түзулер аксиомалары орындалады.
Жоғарыда қабылданған аксиомалардан әр жазықтықта планиметрияның теоремаларын қолдануға болатындығы шығады.
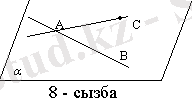 3. 1-с а л д а р. Түзу мен оған тиісті емес нүкте арқылы бір, тек бір ғана жазықтық жүргізуге болады.
3. 1-с а л д а р. Түзу мен оған тиісті емес нүкте арқылы бір, тек бір ғана жазықтық жүргізуге болады.
Дәлелдеуі:
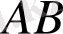 түзуі және онда жатпайтын
түзуі және онда жатпайтын
 нүктесі берілсін (7-сурет) .
нүктесі берілсін (7-сурет) .
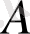 және
және
 нүктелері арқылы түзу
нүктелері арқылы түзу
жүргізейік (аксиома-2) .
 нүктесі
нүктесі
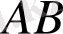 түзуінде жатпайтындықтан
түзуінде жатпайтындықтан
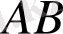 және
және
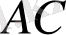 түзулері әртүрлі. 7-сурет
түзулері әртүрлі. 7-сурет
Сонымен қатар
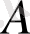 ,
,
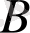 ,
,
 нүктелері бір түзудің бойында жатпайды. Олай болса, аксиома-4 бойынша
нүктелері бір түзудің бойында жатпайды. Олай болса, аксиома-4 бойынша
 жазықтығын жүргізуге болады.
жазықтығын жүргізуге болады.
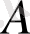 ,
,
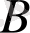 ,
,
 нүктелері
нүктелері
 жазықтығында жатқандықтан
жазықтығында жатқандықтан
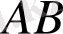 ,
,
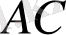 түзулері де осы жазықтыққа тиісті екені белгілі. Бұл түзулердің ортақ
түзулері де осы жазықтыққа тиісті екені белгілі. Бұл түзулердің ортақ
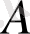 нүктесі болғандықтан, олар қиылысатын түзулер.
нүктесі болғандықтан, олар қиылысатын түзулер.
2-с а л д а р. Қиылысатын екі түзу арқылы бір, тек бір ғана жазықтық жүргізуге болады.
3-с а л д а р. Әр түрлі екі параллель түзу арқылы тек бір ғана жазықтық жүргізуге болады.
Біз кеңістіктегі
және
екі түзу қиылысушы немесе параллель болуы мүмкін екендігін бұрыннан білеміз. Сонымен қатар екі түзудің кеңістікте өзара орналасуының стереометрияға тән жағдайы болады.
Анықтама. Екі түзу әрі қиылыспаса, әрі параллель болмаса, олар айқас түзулер деп аталады.
А 1
В 1
D 1
C 1
А
В
D
C
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz