Атомдық және ядролық физика: практикум - есептер мен шешімдер


ӘЛ-ФАРАБИ атындағы ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
К. Б. Жұманов, Г. Н. Шынықұлова
АТОМДЫҚ ЖӘНЕ
ЯДРОЛЫҚ ФИЗИКА
ЕСЕПТЕР
Практикум
Алматы
«Қазақ университеті»
2018
ӘОЖ
КБЖ
Ж
Баспаға әл-Фараби атындағы Қазақ ұлттық университеті
физика-техникалық факультетінің Ғылыми Кеңесі және
Редакциялық-баспа кеңесі шешімімен ұсынылған
(№7 хаттама 5 шілде 2018 жыл)
Пікір жазғандар :
Әл-Фараби атындағы ҚазҰУнің теориялық және ядролық физика кафедрасының профессоры , физика-математика ғылымдарының кандидаты Ә. Х. Әбілдаев
физика-математика ғылымдарының кандидаты Ж. Б. Тоқбергенов
Жұманов К. Б.
Ж 81
Атомдық және ядролық физика. Есептер: практикум / Жұманов К. Б., Шынықұлова Г. Н. - Алматы: Қазақ университеті, 2018. - б.
ISBN 978-601-04-3597-1
Практикум жоғары оқу орындарының атомдық және ядролық физика пәнінің типтік бағдарламасының типтік бағдарламасына сәйкес 9 бөлімнен тұрады. Әрбір бөлімде қысқаша теориялық материал, бөлім тақырыптары бойынша есеп шығару үлгілері, студенттің өзіне білімін бағалауға мүмкіндік беретін өз бетімен шығару үшін 200-ден астам есеп, бақылау жұмыстары үшін есептер берілген. Барлық есептердің жауаптары бар. Есептердің шарттарында және жауаптарында СИ бірліктерімен құралған еселік және үлестік бірліктер қолданылған. Есеп шығаруға қажетті анықтамалық материалдар қосымша түрінде келтірілген.
Практикум атомдық және ядролық физика пәні бойынша теориялық материалдардың практикалық қолданылуы және есеп шығарып үйрену үшін студенттерге көмек беретін құрал ретінде ұсынылады.
Кітап жоғары оқу орындарының физика, жылуэнергетикасы, электрэнергетикасы, материалтану мамандықтарының студенттеріне арналған.
© Жұманов К. Б., Шынықұлова Г. Н., 2018
ISBN 978-601-04-3597-1 © Әл-Фараби атындағы ҚазҰУ, 2018
МАЗМҰНЫ
АЛҒЫ СӨЗ 7
- АТОМДЫҚ ФИЗИКАРЕЗЕРФОРД - БОР АТОМЫҚысқаша теориялық кіріспе. Атомның ядролық моделі 8Есеп шығару үлгілері
Атомның Резерфорд ұсынған моделі
Сутегі атомының Бор ұсынған теориясы
- Өз бетімен шығару үшін есептер. α-бөлшектердің шашырауы 28
Атомның Бор ұсынған моделі. Сутегі тәрізді иондар спектрі
1. 1. 4. Резерфорд-Бор атомы» тақырыбы бойынша бақылау
жұмыстары үшін есептер 30
1. 2. БІР ЭЛЕКТРОНДЫ АтомдыҚ ЖҮЙЕЛЕР.
СІЛТІЛІК МЕТАЛЛ АТОМДАРЫ
- Қысқаша теориялық кіріспе Бір электронды атомдар 32
Сілтілік металл атомдары энергиясының меншікті мәндері
- Есеп шығару үлгілері 44
Сутегі атомы. Шредингер теңдеуі
Сілтілік метал атомдарының спектрлері
Энергия деңгейлері мен спектрлік сызықтардың нәзік түзілісі
- Өз бетімен шығару үшін есептер 63
Сутегі атомы.
Электронның орбиталық импульс және орбиталық
магниттік моменті.
Электронның спиндік импульс моменті және спиндік
магниттік моменті.
Сілтілік металдар атомдарының спектрлері.
Энергия деңгейлері мен спектрлік сызықтардың нәзік түзілісі.
- «Бірэлектронды атомдық жүйелер» тақырыбы бойынша
бақылау жұмыстары үшін есептер 68
- КӨП ЭЛЕКТРОНДЫ АТОМДАРҚысқаша теориялық кіріспе 70
Паули принципі. Электрондық қабаттар мен қабықтардың
толтырылуы
Көп электронды атомның механикалық моменті
Рентгендік спектрлер
- Есеп шығару үлгілері 79
Атомдағы электрондардың күйлері.
Рентген спектрлері.
- Өз бетімен шығару үшін есептер 88
Паули принципі. Электрондық қабықтардың толтырылуы.
Көп электронды атомның механикалық моменті.
Спектрлік термдер.
Рентгендік спектрлер
- «Паули принципі. Рентгендік спектрлер» бойынша
бақылау жұмыстары үшін есептер 93
- АТОМНЫҢ МАГНИТТІК ҚАСИЕТТЕРІҚысқаша теориялық кіріспе 94
Атомның магниттік моменті.
Магнит өрісінің атомға әсері.
- Есеп шығару үлгілер 98
Атомның магниттік моменті.
Зееман эффекті.
- Өз бетімен шығару үшін есептер 104
Атомның магниттік моменті.
Магнит өрісінің атомға әсері. Зееман эффекті.
Магниттік резонанс.
- «Атомның магниттік қасиеттері» тақырыбы бойынша
бақылау жұмыстары үшін есептер 106
1. 5. Екі атомды молекулалар
1. 5. 1. Қысқаша теориялық кіріспе 108
Молекуланың айналысы
1. 5. 2. Молекуланың тербелісі 110
1. 5. 3. Екі атомды молекулалардың электрондық спектрлері 115
1. 5. 4. Есеп шығару үлгілері 117
Айналыс спектрлері.
Тербеліс спектрлері.
1. 5. 5. Өз бетімен шығару үшін есептер 125
Молекуланың айналысы.
Айналыс спектрлері.
Молекуланың тербелісі.
Екі атомды молекулалардың тербеліс спектрлері.
Екі атомды молекулалардың тербеліс-айналыс спектрлері.
1. 5. 6. «Екі атомды молекулалар» бойынша бақылау жұмыстары
үшін есептер 129
- ЯДРОЛЫҚ ФИЗИКА НЕГІЗДЕРІ
2. 1. АТОМДЫҚ ЯДРОЛАРДЫҢ НЕГІЗГІ ҚАСИЕТТЕРІ
2. 1. 1. Қысқаша теориялық кіріспе 132
Ядролардың құрамы және сипаттамалары.
Ядролық күштер. Ядроның массасы және байланыс энергиясы.
2. 1. 2. Есеп шығару үлгілері 137
Атомдық ядролардың негізгі қасиеттері.
Ядро массасының ақауы, ядроның байланыс энергиясы,
меншікті байланыс энергиясы.
- Өз бетімен шығару үшін есептер 150
Ядролардың құрамы, радиусы, массасы, заряды.
Ядроның массалық ақауы, байланыс энергиясы, меншікті
байланыс энергиясы.
- «Ядролардың құрамы, радиусы, массасы және байланыс
энергиясы» тақырыбы бойынша бақылау жұмыстары
үшін есептер 153
- РАДИОАКТИВТІКҚысқаша теориялық кіріспе 154
Радиоактивтік. Радиоактивтік ыдыраудың негізгі заңы.
Радиоактивтіктің негізгі түрлері.
Альфа - ыдырау.
Бета - ыдырау.
Ядролардың гамма сәуле шығару
Мёссбауэр эффекті
- Есеп шығару үлгілері 166
Радиоактивті ыдырау заңы.
Активтік. Меншікті активтік.
α - ыдырау.
β - ыдырау.
γ - сәуле шығару.
- Өз бетімен шығару үшін есептер 202
Радиоактивті ыдырау заңы
Активтік. Меншікті активтік
α-ыдырау
β-ыдырау
γ-сәуле шығару
- «Радиоактивті ыдырау заңы. Активтік. Меншікті
активтік. Α-ыдырау. Β-ыдырау. γ-сәуле шығару»
тақырыптары бойынша бақылау жұмыстары
үшін есептер 208
- ЯДРОЛЫҚ РЕАКЦИЯЛАР ЖӘНЕ БҰЛАРДЫҢ
НЕГІЗІ ТҮРЛЕРІ
- Қысқаша теориялық кіріспе 209
Ядролық реакциялар.
Ядролардың бөлінуі.
Атомдық ядролардың синтезі.
2. 3. 2. Есеп шығару үлгілері 219
Ядролық реакциялар.
Ядроның бөлінуі.
Термоядролық реакция.
2. 3. 3. Өз бетімен шығару үшін есептер 235
Ядролық реакциялар
- ЭЛЕМЕНТАР БӨЛШЕКТЕРҚысқаша теориялық кіріспе 240Есеп шығару үлгілері 245
Элементар бөлшектер
- Өз бетімен шығару үшін есептер 252
- «Ядролық реакциялар. Элементар бөлшектер» бойынша
бақылау жұмысы үшін есептер 253
Жауаптар 255
ҚОСЫМШАЛАР 268
БИБЛИОГРАФИЯЛЫҚ ТІЗІМ 273
АЛҒЫ СӨЗ
Ұсынылып отырған есептер жинағы атомдық және ядролық физика бойынша есеп шығаруды үйрену үшін студентке көмек беретін құрал болып табылады. Пәннің типтік оқу бағдарламасына сәйкес барлық есептер: «Резерфорд - Бор атомы», «Бір электронды атомдық жүйелер», «Көп электронды атомдар», «Атомның магниттік қасиеттері», «Атомдық ядролардың құрамы мен қасиеттері», «Радиоактивтік», «Ядролық реакциялар», «Элементар бөлшектер» сияқты сегіз бөлімге бөлінген. Бөлімдегі есептер тақырыптар бойынша орналастырылған. Әрбір бөлімде 1) алдымен есептердің мазмұн-мағынасын түсіну және оларды шығару үшін қажетті негізгі физикалық ұғымдар, шамалардың тұжырымдамалары мен түсіндіруі және формулалар қамтылған қысқаша теориялық материал баяндалады; 2) бұдан кейін есептің қалай шығарылғаны түсіндіріледі. Бұл үшін күрделілік деңгейі әр түрлі оншақты есеп толық қарастырылады; 3) әрбір бөлім соңында студенттің өз бетімен шығаруы үшін есептер, бақылау жұмысы үшін есептер берілген. Есептер көп тараған белгілі есептер жинақтарынан [1-14] алынды.
Барлық есептердің жауаптары берілген. Есептердің шарттарында және жауаптарында СИ бірліктерінен құралған еселік және үлестік бірліктер қолданылған.
Есептерді шығарғанда мына әдістемелік нұсқауларды пайдаланған жөн:
- Есептің шартын жете ұғынып алып, есепте берілген шамаларды, нені табу керектігін қысқаша жазып алып, барлығын СИ-де өрнектеп, есептің мазмұнын түсіндіретін сызба-сурет салу керек.
- Берілген есептің негізіне қандай физикалық заңдар алынғанын анықтап, есепті жалпы түрде, яғни ізделіп отырған физикалық шаманы есепте берілген шамалар арқылы (аралық формулаларға сан мәндерін қоймай, әріптік белгілер арқылы) өрнектеп шығару керек.
- Жалпы шешімнің дұрыстығын тексеріп алып, аяққы формулаға сан мәндерін қойып, оның өлшемділігін тексеріп, табылған физикалық шаманың бірлігін көрсету керек.
1. АТОМДЫҚ ФИЗИКА
1. 1. 1. Қысқаша теориялық кіріспе
Атомның ядролық моделі. Атом оң зарядталған ядродан және оны қоршаған теріс зарядталған электрондардан (электрондық қабық) тұратындығы тағайындалған. Ядроның сызықтық мөлшері 10 -15 -10 -14 м шамасында. Атомның электрондық қабығымен анықталатын өзінің мөлшері бұдан 10 5 еседей үлкен. Бірақ атомның түгелге дерлік массасы (99, 95 %) ядрода шоғырланған.
Атомның осы моделін 1911 жылы Резерфорд α-бөлшектердің өте жұқа алтын фольгадан (қабыршақтан) шашырауы бойынша тәжірибе нәтижелеріне сүйеніп, ұсынған. Сондықтан ол Резерфорд моделі деп аталады.
Қозғалмайтын ядроның кулондық өрісінен зарядталған бөлшектің (α-бөлшек) шашырайтын θ бұрышы
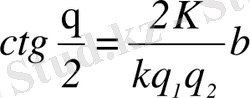 немесе
немесе
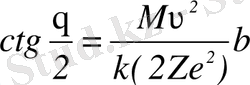 (1. 1. 1)
(1. 1. 1)
формуласымен анықталады, мұндағы
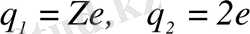 - әсерлесетін бөлшектердің (ядро және α-бөлшек) зарядтары,
- әсерлесетін бөлшектердің (ядро және α-бөлшек) зарядтары,
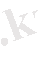
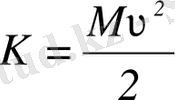 - түсетін бөлшектің кинетикалық энергиясы, М -α-бөлшектің массасы, υ - оның ядродан алыстағы жылдамдығы,
- түсетін бөлшектің кинетикалық энергиясы, М -α-бөлшектің массасы, υ - оның ядродан алыстағы жылдамдығы,
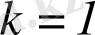 (
СГС
)
,
(
СГС
)
,
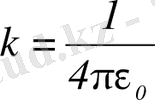 (СИ) .
(СИ) .
Атомдық құбылыстар аймағында тәжірибеде (1. 1. 1) формуланың өзін емес, осы формуланың статистикалық салдарын тексеруге болады. Осы жағдайда α-бөлшектің dΩ денелік бұрышқа шашырауы үшін ядроның дифференциалдық тиімді қимасы, шашыраудың толық қимасы ұғымдары енгізіледі.
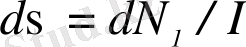 - шашыраудың дифференциалдық тиімді қимасы деп атомнан (ядродан) уақыт бірлігінде
dΩ
денелік бұрышқа шашыраған
- шашыраудың дифференциалдық тиімді қимасы деп атомнан (ядродан) уақыт бірлігінде
dΩ
денелік бұрышқа шашыраған
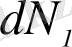 бөлшектер санының түсетін бөлшектер ағынының І тығыздығына (І интенсивтілігіне) қатынасын айтады; І - ағынға перпендикуляр бірлік аудан арқылы бірлік уақыт ішінде өтетін шоқтағы α-бөлшек саны.
бөлшектер санының түсетін бөлшектер ағынының І тығыздығына (І интенсивтілігіне) қатынасын айтады; І - ағынға перпендикуляр бірлік аудан арқылы бірлік уақыт ішінде өтетін шоқтағы α-бөлшек саны.
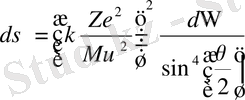 , (1. 1. 2)
, (1. 1. 2)
мұндағы
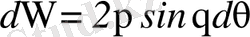 денелік бұрыш элементі. (1. 1. 2) формуламен Резерфордтың атомның ядролық моделін ұсынуына негіз болған эксперименттік деректер түсіндіріледі. (1. 1. 2) формула α-бөлшектердің бір ядродан шашырауын бейнелейді. Егер шашыратқыш фольгада ядроның тығыздығы n болса, онда олардың жалпы саны nV болады, мұндағы V - фольганың көлемі. Сонымен, шашыраған α-бөлшектер саны:
денелік бұрыш элементі. (1. 1. 2) формуламен Резерфордтың атомның ядролық моделін ұсынуына негіз болған эксперименттік деректер түсіндіріледі. (1. 1. 2) формула α-бөлшектердің бір ядродан шашырауын бейнелейді. Егер шашыратқыш фольгада ядроның тығыздығы n болса, онда олардың жалпы саны nV болады, мұндағы V - фольганың көлемі. Сонымен, шашыраған α-бөлшектер саны:
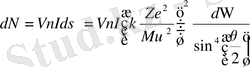 (1. 1. 3)
(1. 1. 3)
формуламен анықталады.
Бөлшектердің бастапқы қозғалыс бағытына θ бұрышпен dΩ элементар денелік бұрышқа шашыраған бөлшектердің салыстырмалы саны үшін Резерфорд формуласы:
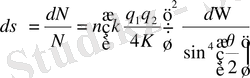 , (1. 1. 4)
, (1. 1. 4)
мұндағы n - фольга бетінің бірлік ауданына келетін ядро саны, К - фольгаға түсетін бөлшектердің (α-бөлшектер) кинетикалық энергиясы,
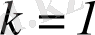 (СГС) немесе
(СГС) немесе
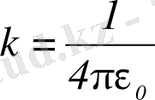 (СИ),
(СИ),
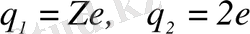 - әсерлесетін бөлшектердің зарядтары.
- әсерлесетін бөлшектердің зарядтары.
Бальмердің жалпыланған формуласы
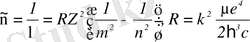 (м
-1
),
(м
-1
),
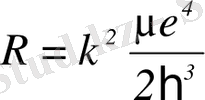 (с
-1
) (1. 1. 5)
(с
-1
) (1. 1. 5)
қарапайым атом-сутегі атомының (
z=1
) және сутегі тәрізді иондар (
z>1, He
+
, Li
+
+
, …) спектрлеріндегі серияларды бейнелейді;
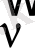 - спектрдегі спектрлік сызықтардың толқындық саны; R - Ридберг тұрақтысы; m серияны анықтайды (
m=
1, 2, …) ; n тиісті серияның жеке сызықтарын анықтайды (n = m + 1, m + 2, …) .
- спектрдегі спектрлік сызықтардың толқындық саны; R - Ридберг тұрақтысы; m серияны анықтайды (
m=
1, 2, …) ; n тиісті серияның жеке сызықтарын анықтайды (n = m + 1, m + 2, …) .
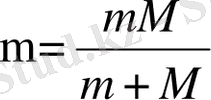 жүйенің келтірілген массасы (m<<M болғанда μ≈m), z - ядро заряды.
жүйенің келтірілген массасы (m<<M болғанда μ≈m), z - ядро заряды.
R
=3, 29⋅10
15
c
-1
,
R
=109677, 581 см
-1
;
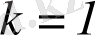 (СГС) ,
(СГС) ,
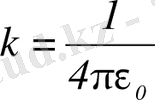 (СИ) .
(СИ) .
Атомның Бор ұсынған моделі (1913) . Н. Бор сутегі атомының бүкіл спектрін өте жақсы түсіндіретін және атом құрылысының физикалық моделі негізіне алынған теория ұсынды. Бор моделіне сәйкес атомдағы электрондар ядроны орнықты (стационарлық) дөңгелек орбиталар бойынша айналып жүреді. Осы орбиталарға электронның белгілі энергиялары сәйкес келеді. Бір орбитадан екінші орбитаға секіріп, электрондар энергияны қабылдап немесе жоғалта алады.
Бор теориясында сызықтық спектрлердің эмпирикалық заңдылықтары, Резерфордтың ядролық моделі және жарықтың шығарылуы және жұтылуының кванттық сипаты біртұтас біріктірілді.
Бордың бірінші постулаты. Атомда энергияның белгілі дискреттік мәндерімен сипатталатын стационарлық (уақыт бойынша өзгермейтін) күйлер болады, осы күйлерде ол энергия шығармайды.
Атомның стационарлық күйлеріне стационарлық орбиталар сәйкес келеді, осы орбиталар бойынша электрондар қозғалады. Стационар орбиталар бойынша электрондардың қозғалысы кезінде электрмагниттік сәуле шығарылмайды. Атомның стационарлық күйінде электрон дөңгелек орбита бойымен қозғалып,
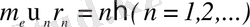 (1. 1. 6)
(1. 1. 6)
шартын қанағаттандыратын, импульс моментінің дискретті квантталған мәндеріне ие болуы тиіс.
Бордың екінші постулаты. Электрон бір орбитадан басқасына ауысқанда энергиясы тиісті стационар күйлердің энергиялары айырымына тең
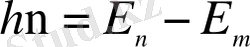 (1. 1. 7)
(1. 1. 7)
бір энергия кванты - фотон шығарылады (жұтылады) .
Кванттық ауысулардың дискретті жиіліктерінің мүмкін болатын жиыны
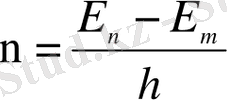 (1. 1. 7 а)
(1. 1. 7 а)
атомның сызықтық спектрін анықтайды.
n i - стационарлық орбита радиусы:
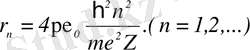 . (1. 1. 8)
. (1. 1. 8)
Бірінші Бор радиусы:
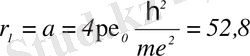 пм. (1. 1. 8 а)
пм. (1. 1. 8 а)
Сутегі тәрізді жүйедегі электронның толық знергиясы:
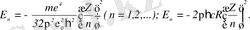 (1. 1. 9)
(1. 1. 9)
Мұнда ядро (протон) массасы электрон массасынан ∞ ауыр (m << M) деп алғанда Ридберг тұрақтысы
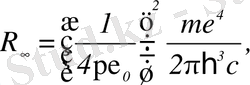 м
-1
(1. 1. 10)
м
-1
(1. 1. 10)
былай өрнектеледі.
Ал М ядро массасының (протон) шектеулігі ескерілгенде m электрон массасын
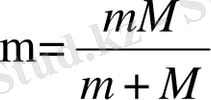 келтірілген массаға ауыстыру керек. Сонда Ридберг тұрақтысы ядро массасына тәуелді болады:
келтірілген массаға ауыстыру керек. Сонда Ридберг тұрақтысы ядро массасына тәуелді болады:
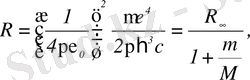 м
-1
. (1. 1. 11)
м
-1
. (1. 1. 11)
R Ридберг тұрақтысының ядро массасына тәуелділігі спектрлік сызықтардың изотоптық ығысуында білінеді:
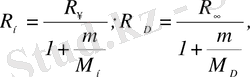 (1. 1. 12)
(1. 1. 12)
мұндағы R ∞ =109737, 3534 см -1 , R н = 109677, 581 см -1 ,
R D = 109707, 419 см -1 .
 Дейтерий сызықтары толқын ұзындықтарының сутегі сызықтары толқын ұзындықтарына салыстырғанда изотопты ығысуы
Дейтерий сызықтары толқын ұзындықтарының сутегі сызықтары толқын ұзындықтарына салыстырғанда изотопты ығысуы
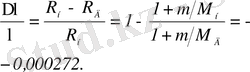
11-сурет
Мысалы, дейтерийдің D
α
бальмер сызығы сутегінің Н
α
сызығына қатысты қысқа толқынды аймаққа қарай
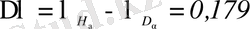 нм аз шамаға ығысады. Бірақ осы ауытқу тәжірибеде айқын байқалады.
нм аз шамаға ығысады. Бірақ осы ауытқу тәжірибеде айқын байқалады.
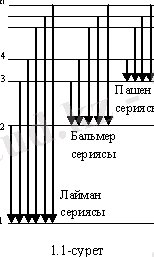
Сутегі атомы және сутегі тәрізді иондардың негізгі серияларының пайда болу (шығарылу) сызбасы ( 1. 1-сурет ) .
1. 1. 2. Есеп шығару үлгілері. Атомның Резерфорд ұсынған моделі
- Гейгер-Марсден тәжірибесінде алтын фольга алынған. α-бөлшектердің кинетикалық энергиясы К = 7, 68 МэВ. Осы тәжірибеде:
а) α-бөлшек алтын атомының (Z = 79) ядросына қандай
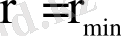 қашықтыққа дейін жақындай алады?
қашықтыққа дейін жақындай алады?
ә) α-бөлшектер θ ≥ 90 ° бұрыштарға шашырауы үшін b көздеу қашықтығы қандай болуы тиіс?
б) ядроның осы жағдайдағы тиімді қимасы қандай болады?
в) егер фольганың қалыңдығы = 6, 0⋅10 -7 м болса, онда 90 ° немесе одан үлкен бұрыштарға ауытқитын α-бөлшектердің салыстырмалы саны қандай болатынын анықтаңыз.
Шешімі:
а)
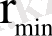 арақашықтықты анықтау үшін кинетикалық энергиясы К және ядродан үлкен қашықтықтағы α-бөлшекті қарастырамыз. Бөлшек ядро центрі бағытында қозғалады. Сонда оның ядроға ең жақын келгендегі
арақашықтықты анықтау үшін кинетикалық энергиясы К және ядродан үлкен қашықтықтағы α-бөлшекті қарастырамыз. Бөлшек ядро центрі бағытында қозғалады. Сонда оның ядроға ең жақын келгендегі
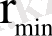 арақашықтыққа сәйкес келетін нүктеде α-бөлшек пен алтын ядросы арасындағы тебіліс күші әсерінен, α-бөлшек қас-қағым сәтке тоқтайды. Ал оның К кинетикалық энергиясы α-бөлшек-ядро жүйесінің электрстатикалық потенциалдық әсерлесу энергиясына ауысады:
арақашықтыққа сәйкес келетін нүктеде α-бөлшек пен алтын ядросы арасындағы тебіліс күші әсерінен, α-бөлшек қас-қағым сәтке тоқтайды. Ал оның К кинетикалық энергиясы α-бөлшек-ядро жүйесінің электрстатикалық потенциалдық әсерлесу энергиясына ауысады:
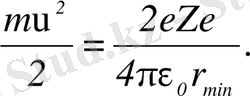 (1)
(1)
Осы теңдіктен
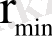 -ді табамыз:
-ді табамыз:
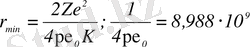 Н⋅м
2
⋅Кл
-2
;
Н⋅м
2
⋅Кл
-2
;
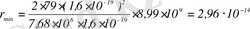 м.
м.
ә) (1. 1. 1) өрнегінен θ шашырау бұрышы b-ға тәуелді екендігі және неғұрлым b кіші болса, θ шашырау бұрышы солғұрлым үлкен болатындығы көрінеді. (1. 1. 1) формуланы (1) теңдігімен анықталатын α-бөлшектің ядроға ең жақын келу
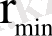 қашықтығы арқылы өрнектеуге болады. Осы жағдайда
қашықтығы арқылы өрнектеуге болады. Осы жағдайда
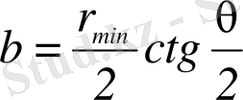 . (2)
. (2)
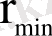 мәні үшін және θ=90
0
болғанда
мәні үшін және θ=90
0
болғанда
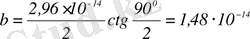 м.
м.
б) ядроға ≤b көздеу қашықтықпен жақындайтын α-бөлшектердің бәрі ≥θ≥90 ° бұрыштармен шашырайтын болады. Ядро айналасындағы радиусы b-ға тең шеңбердің ішіне кіретін аймақтың ауданы ≥θ бұрышқа шашыраудың интегралдық тиімді қимасы деп аталады. Ол мынаған тең болады:
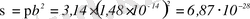 м
2
.
м
2
.
в) α-бөлшектер шоғының көлденең қимасын S арқылы белгілейік. Сонда шоқтың жолындағы фольгадағы атом (ядро) саны nS болады, мұндағы n - бірлік көлемдегі ядро саны, - фольганың қалыңдығы. Демек, θ бұрышынан үлкен бұрыштарға шашырағанда және көздеу қашықтықтары b-дан кіші болғанда осы ядролардың тиімді қималарынан түзілген шашыратушы нысананың тиімді қимасын nσS деп жазуға болады.
S-нысананың жалпы ауданы болатындықтан, ≥θ бұрыштарға шашырайтын α-бөлшектердің салыстырмалы саны
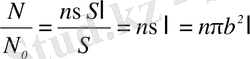
өрнегімен анықталады.
Бірлік көлемдегі n ядро санын мына формула бойынша есептеп табуға болады:
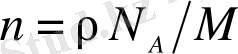 ,
,
мұндағы, ρ=1, 93⋅10 4 кг/м 3 - алтынның тығыздығы, М=0, 197кг/моль - мольдык масса, N A =6, 02⋅10 23 моль -1 - Авогадро саны. Сонда:
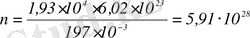 м
-3
,
м
-3
,
Ал
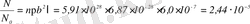 .
.
Осы нәтиже мынаны көрсетеді: 1 α-бөлшектің шамамен екеуі θ≥90 ° бұрышқа ауытқиды екен. Сонымен, қалыңдығы осындай алтын фольга α-бөлшектер үшін біршама мөлдір деген қорытынды жасауға болады.
2. Кинетикалық энергиясы К α = 40 кэВ α-бөлшек бетпе-бет соқтығысқанда: а) тыныштықта тұрған қорғасын ядросына; ә) алғашында тыныштықта болған 7 Li ядросына қандай ең кіші қашықтыққа дейін жақындай алады?
Шешімі: а) α-бөлшек қорғасын атомының ядросымен әсерлескенде ядро қозғалмайды деп аламыз. Ядроның электр өрісі α-бөлшекке тежеуші әрекет етеді. Осыған байланысты бөлшектің кинетикалық энергиясы кемиді; мұның есесіне бөлшек-ядро жүйесінің потенциалдық энергиясы артады. Ең кіші қашықтыққа дейін жақындау мезетінде α-бөлшек тоқтайды. Осы жағдай үшін жүйенің потенциалдық энергиясы α-бөлшектің кинетикалық энергиясының кеміген шамасына тең болады:
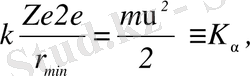
мұндағы, Z=82-қорғасынның атомдық нөмірі;
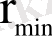 -ең жақын келгендегі қашықтық; υ-α-бөлшектің ядродан алыста болғандағы жылдамдығы, m және 2е - α-бөлшектің массасы мен заряды.
-ең жақын келгендегі қашықтық; υ-α-бөлшектің ядродан алыста болғандағы жылдамдығы, m және 2е - α-бөлшектің массасы мен заряды.
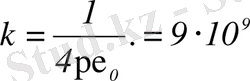 Нм
2
/Кл
2
.
Нм
2
/Кл
2
.
Осыдан:
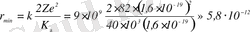 м.
м.
Бұдан ядро радиусы 10 -12 м шамасынан асып кетпейді деген қорытынды жасауға болады.
ә) α-бөлшек-ядро жүйесі тұйық деп ұйғарылады, сондықтан бұлардың бір-біріне жақындау үдерісінде жүйенің импульсі де, механикалық энергиясы да сақталады. Осыдан екі жағдай үшін α-бөлшек ядродан алыста болғанда және ядроға ең жақын келген мезетте (осы жағдайда жүйе біртұтас болып қозғалады), мына теңдіктерді жазамыз:
импульстың сақталу заңы: р α = р α+Li , (1)
энергияның сақталу заңы:
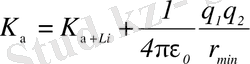 , (2)
, (2)
мұндағы, q 1 және q 2 -α-бөлшектің және Lі ядросының зарядтары. К кинетикалық энергия мен р импульстың К=p 2 /2m байланысын ескеріп, (1) теңдікті К арқылы өрнектейміз:
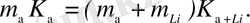 (3)
(3)
Соңғы теңдіктен К α+Li -ді тауып, алынған өрнекті (2) теңдеуге қоямыз:
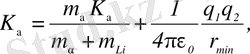
осыдан
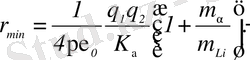
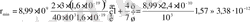 м.
м.
- Сутегі ядросын радиусы r0=0, 5⋅10-8см орбита бойымен айнала қозғалатын электрон, егер де ол энергиясын классикалық электрдинамикаға сәйкес сәуле шығаруға жоғалтатын болса, онда ол ядроға қанша уақыт ішінде құлаған болар еді? Осы уақытты бағалаңыз.
Шешімі: Оңайлық үшін ядроға кез келген құлау мезетінде электрон шеңбер бойымен бірқалыпты қозғалады деп санаймыз. Сонда Ньютонның 2-заңына сәйкес:
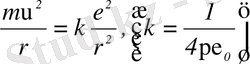 . (1)
. (1)
Осыдан электронның үдеуі:
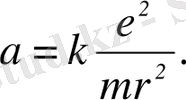 (2)
(2)
Электронның кинетикалық энергиясы:
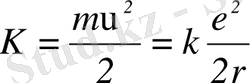 , (3)
, (3)
және электронның ядро өрісіндегі толық энергиясы:
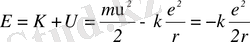 (4)
(4)
болады. Классикалық электрдинамикаға сәйкес зарядталған бөлшектің сәуле шығару салдарынан энергиясының кемуі бірлік уақытта:
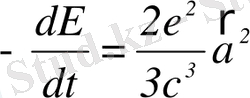 (5)
(5)
формуласымен анықталады.
(2) өрнегін ескеріп, (4) және (5) теңдеулерінен
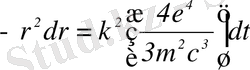 (6)
(6)
теңдеуін аламыз.
Осы теңдеуді r бойынша r 0 -ден 0-ге дейін және t бойынша 0-ден τ-ға дейін интегралдаймыз. Нәтижесінде электронның ядроға құлау уақыты мынаған тең болады:
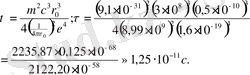
Сутегі атомының Бор ұсынған теориясы
- Сутегі атомы толқын ұзындығы λ = 4, 86⋅10-7м фотон шығарады. Атомдағы электронның энергиясы қандай шамаға өзгергендігін анықтаңыз.
Шешімі:
Бор теориясы бойынша электрон энергиясы Е
n
күйден энергиясы E
m
күйге ауысқанда энергиясы
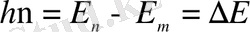 болатын фотон шығарады. Демек, электрон энергиясы шығарылған фотон энергиясына тең шамаға өзгереді. ν = c/λ қатынасын ескереміз. Сонда
болатын фотон шығарады. Демек, электрон энергиясы шығарылған фотон энергиясына тең шамаға өзгереді. ν = c/λ қатынасын ескереміз. Сонда
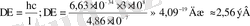 .
.
- Сутегі атомындағы бірінші Бор радиусын және осы орбитадағы электронның қозғалыс жылдамдығын анықтаңыз.
Шешімі: Ядро заряды Ze-ге тең сутегі тәрізді ионның n-і орбитасының радиусы
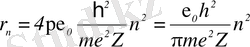
формуламен анықталады.
Мұндағы, n-орбита нөмірі; m-электрон массасы.
n=1 және Z=1 болғанда
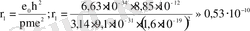 м.
м.
Бордың бірінші постулаты бойынша n-і орбитадағы электронның импульс моменті
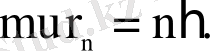
Сонда
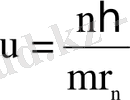 және n=1 болғанда
және n=1 болғанда
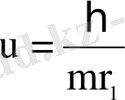 ,
,
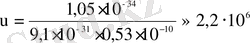 м/с.
м/с.
- Электрондар кванттық ауысу жасағанда Лайман, Бальмер және Пашен серияларындағы шығарылатын фотондардың ең үлкен және ең кіші толқын ұзындықтарын анықтаңыз.
Шешімі: Бальмердің жалпыланған формуласы сутегі атомындағы электрон барлық мүмкін болатын ауысулар жасағанда пайда болатын λ толқын ұзындықтарды анықтауға мүмкіндік береді:
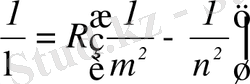 немесе
немесе
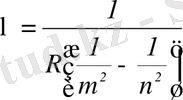 .
.
Лайман сериясында бірінші орбитаға қалған барлық орбиталардан ауысу іске асады, яғни: m=1, n=2, 3, . ., ∞.
Демек,
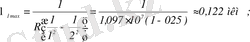
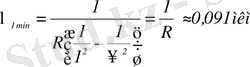
Бальмер сериясында ауысу екінші орбитаға қалған барлық жоғары орналасқандардан іске асады, яғни: m=2; n=3, 4, . . ∞.
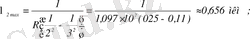
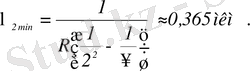
Пашен сериясында ауысу үшінші орбитаға жоғары орналасқан орбиталардан іске асады, яғни: m=3, n=4, 5, …∞.
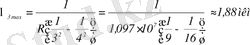
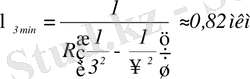
- Қоздырылған тыныштықта тұрған сутегі атомы Лайман сериясының бас сызығына сай келетін фотонды шығарғаннан кейін қандай жылдамдық қабылдағанын анықтаңыз.
Шешімі: Атом-фотон жүйесі үшін энергияның және импульстің сақталу заңдары:
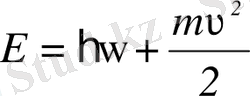 (1)
(1)
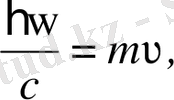 (2)
(2)
Мұндағы,
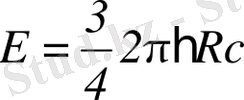 - атомның қоздырылу энергиясы, ω- фотон энергиясы, m және υ- атомның массасы мен жылдамдығы. (1) және (2) теңдеулерінен атомның фотон шығарғаннан кейін қабылдайтын жылдамдығы үшін өрнек алынады:
- атомның қоздырылу энергиясы, ω- фотон энергиясы, m және υ- атомның массасы мен жылдамдығы. (1) және (2) теңдеулерінен атомның фотон шығарғаннан кейін қабылдайтын жылдамдығы үшін өрнек алынады:
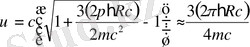 ,
,
мұнда,
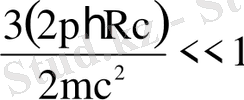 болатындығы ескерілді.
болатындығы ескерілді.
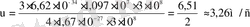
- Сутегі атомының иондану потенциалын және бірінші қозу потенциалын анықтау керек.
Шешімі:
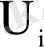 иондану потенциалы деп берілген қоздырылмаған атоммен соқтығысқанда оны иондау үшін қажетті үдеткіш өрісте электрон өтуге тиіс ең аз потенциалдар айырымын айтады. Атомнан электронды аластауға жұмсалатын
А
і
жұмысы электронды үдететін электр өрісінің
иондану потенциалы деп берілген қоздырылмаған атоммен соқтығысқанда оны иондау үшін қажетті үдеткіш өрісте электрон өтуге тиіс ең аз потенциалдар айырымын айтады. Атомнан электронды аластауға жұмсалатын
А
і
жұмысы электронды үдететін электр өрісінің
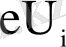 жұмысына тең, сондықтан:
жұмысына тең, сондықтан:
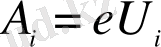 . (1)
. (1)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz