Сандардың бөлінгіштігі, көпмүшелерді жіктеу және теңсіздіктерді дәлелдеу әдістері


ЛЕКЦИЯ № 1 Сандардың бөлінгіштігі
Жоспар:
1. Сандардың бөлінгіштік белгілері. Паскаль белгісі.
2. Натурал санның қарапайым жіктелуі
3. Арифметиканың негізгі теоремасы
4. Натурал сандардың бөлгіштер санын және бөлгіштерінің қосындысын анықтау
1. Сандардың бөлінгіштік белгілері. Паскаль белгісі.
Сандардың бөлінгіштік белгілерін салыстыру жәрдемімен тағайындауға болатындығын ең алғаш француз математигі Блез Паскаль(1623-1682) көрсеткен.
Кез келген N натурал санының m натурал санға бөлінуінің қажетті және жеткілікті шартын сипаттайтын ереже N -нің m -ге бөліну белгісі делінеді. Ол белгі g жүйеде жазылған кез келген натурал санның цифрлары арқылы, сол санның берілген m санға бөлінетіндігін немесе бөлінбейтіндігін ажыратуға мүмкіндік береді . Француз Блез Паскаль натурал сандардың бөлінгіштігінің жалпы белгісін тұжырымдаған .
Паскаль белгісі . g санау жүйесінде жазылған N= a n g n + a n-1 g n-1 +…+ + a 1 g + a 0 натурал саны m натурал санына бөліну үшін Q=a n r n + + a n-1 r n-1 +…+ a 1 r 1 + a 0 натурал саны m -ге бөлінуі қажетті және жеткілікті. Мұндағы r i саны g i санын m- ге бөлгендегі қалдық.
Енді кейбір сандардың бөлінгіштік белгілерін келтірелік.
2-ге бөлінгіштік белгі. Егер санның соңғы цифры нөл немесе 2, 4, 6, 8 болса, онда бұл сан 2-ге қалдықсыз бөлінеді. Мысалы: 24, 654, 326, 320.
Соңғы цифрлары 0, 2, 4, 6, 8 болған сандар жұп сандар деген тұжырымға келеміз.
2) 4-ке бөлінгіштік белгі. Егер санның соңғы екі цифры да нөл болса немесе осы соңғы екі цифрдан құралган екі таңбалы сан 4-ке бөлінсе, онда бұл сан 4-ке қалдықсыз бөлінеді. Мысалы: 648:4; 123456:4; 8700:4. Себебі 48, 56, 100 сандары 4 ке қалдықсыз бөлінеді .
3) 5-ке бөлінгіштік белгі. Егер сан 0 немесе 5 цифрымен аяқталса, онда бұл сан 5-ке қалдықсыз бөлінеді. Мысалы: 125; 5; 130; 565; 166605; сандары 5-ке қалдықсыз бөлінеді. Себебі соңғы цифрлары 0 немесе 5 цифрымен аяқталған.
4) 3 пен 9-ға бөлінгіштік белгі. Егер санның құрамындағы цифрлардың қосындысы 3-ке (9-ға) бөлінсе, онда бұл сан 3-ке (9-ға) қалдықсыз бөлінеді.
1-мысал. 147 санының 3-ке бөлінетін, бөлінбейтінін білу үшін, ол санның цифрларының косындысын табамыз: 1+4+7=12, 12:3=4, олай болса 147 саны 3-ке қалдықсыз бөлінеді яғни 147:3=49 болады.
2-мысал 384 санының 3-ке бөлінгіштігін анықтау
 .
.
Әрбір қосылғыш 3 ке бөлінеді екен. Олай болса берілген 384 саныда 3 ке қалдықсыз бөлінеді екен.
3-мысал 783 санының 9-ға бөлінгіштігін анықтау
 Әрбір қосылғыш 9 ға бөлінеді екен. Олай болса берілген 783 саныда 9 ға қалдықсыз бөлінеді екен.
Әрбір қосылғыш 9 ға бөлінеді екен. Олай болса берілген 783 саныда 9 ға қалдықсыз бөлінеді екен.

783 саны 9-ға бөліне ме? Санның цифрларының қосындысы 7+8+3=18. 18 саны 9-ға бөлінеді. Демек 783
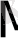 9.
9.
4-мысал.
 санының оң және сол жағына қандай цифрды тіркегенде, ол
санының оң және сол жағына қандай цифрды тіркегенде, ол
 -ге қалдықсыз бөлінеді?
-ге қалдықсыз бөлінеді?
Шешу: 27 саны 3-ке және 9-ға бөлінеді. Берілген 97 санының цифрларының қосындысы 16 болғандықтан, оның 3-ке және 9-ға бөлінуі үшін қосынды 18, 27, 36, . . . болуы мүмкін. Сондықтан 1 цифрын алуға болады, яғни 1971 саны 27-ге қалдықсыз бөлінеді. Кейінгі қосынды 27 (36) болуы үшін алдыңғы қосынды 16-ға 11-ді (20-ны) қосу керек. Олар екі таңбалы сан болғандықтан, есептің шартына сәйкес келмейді.
Сонымен,
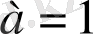 , ізделінді сан -
, ізделінді сан -
 .
.
Жауабы: 1 цифры.
5-мысал. Олимпиада ойындарында тек аңдар! Тасбақаларды есептейміз.
Рептилияның командасында тек тасбақа болды. Тасбақалар саны
 -ден көп, бірақ
-ден көп, бірақ
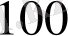 -ден аз. Олимпиада ойындарының ашылу салтанатында бұл команданы 2, 3 немесе 4 тен құралған жануарлар қатарына орналастыруға мүмкін болмады, өйткені бір жануар соңғы қатарда әрқашан жетпеді.
-ден аз. Олимпиада ойындарының ашылу салтанатында бұл команданы 2, 3 немесе 4 тен құралған жануарлар қатарына орналастыруға мүмкін болмады, өйткені бір жануар соңғы қатарда әрқашан жетпеді.
Сондықтан әр қатарда
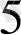 жануардан тұратын тасбақа командасын құруға тура келді. Рептилия командасында қанша тасбақа болды?
жануардан тұратын тасбақа командасын құруға тура келді. Рептилия командасында қанша тасбақа болды?
Шешу:
Егер тасбақалар саны
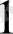 -ге ұлғайтылса, ол
-ге ұлғайтылса, ол
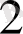 ,
,
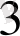 ,
,
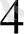 -ке бөлінеді. Осы сандардың ең кіші ортақ еселігі
-ке бөлінеді. Осы сандардың ең кіші ортақ еселігі
 . Есеп шартына сәйкес тасбақалар саны
. Есеп шартына сәйкес тасбақалар саны
 -ден көп және
-ден көп және
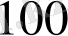 -ден аз болуы үшін: олардың саны
-ден аз болуы үшін: олардың саны
 ,
,
 ,
,
 және
және
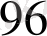 -дан аспайды. Тасбақалар саны көрсетілген сандардан
-дан аспайды. Тасбақалар саны көрсетілген сандардан
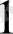 -ге аз болуы және
-ге аз болуы және
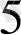 -ке бөлінуі тиіс. Сондықтан қатардағы
-ке бөлінуі тиіс. Сондықтан қатардағы
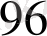 саны ғана жарамды, себебі:
саны ғана жарамды, себебі:
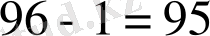 және ол 5-ке қалдықсыз бөлінеді. Сонымен, рептилия командасында
және ол 5-ке қалдықсыз бөлінеді. Сонымен, рептилия командасында
 тасбақа бар екен.
тасбақа бар екен.
Салдар. 6-ға бөлінгіштік белгі. 3-ке бөлінетін жұп сандар 6-ға қалдықсыз бөлінеді. Мысалы: 132:6; 1320:6
5) 11-ге бөлінгіштік белгі. Егер санның құрамындағы тақ орындағы цифрларының қосындысы мен оның жұп орындарындағы цифрларының қосындысының айырмасы нөлге тең немесе 11-ге бөлінетін болса, онда бұл сан 11-ге қалдықсыз бөлінеді.
6-мысал. 1) 7896 және 2) 208912 сандарының 11 ге бөлінетіндігін тексеріңдер.
1)
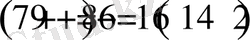 . Нәтижедегі 2 саны 11 ге бөлінбейді, берілген 7896 санда 11 ге бөлінбейді.
. Нәтижедегі 2 саны 11 ге бөлінбейді, берілген 7896 санда 11 ге бөлінбейді.
2)
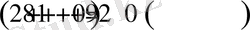 , демек, берілген сан 11 ге бөлінеді:
, демек, берілген сан 11 ге бөлінеді:
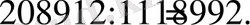
6) 25 ке бөлінгіштік белгі: Егер санның соңғы екі цифры да нөл болса немесе осы соңғы екі цифрлардан құралган екі таңбалы сан 25-ке бөлінсе, онда бұл сан 25-ке қалдықсыз бөлінеді. Мысалы, 500; 8500; сандары 25 ке қалдықсыз бөлінеді.
7) 7-ге бөлінгіштік белгілер (үш түрлі бөлінгіштік белгісін қарастырамыз) :
a) берілген санның соңғы цифрын сызып тастағандағы пайда болған саннан, берілген санның соңғы цифрын екі еселегендегі көбейтіндіні азайтқандағы сан 7-ге бөлінсе, берілген санда 7 ге бөлінеді:
7-мысал.
259 саны 7-ге бөлінеді, себебі
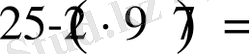 болады. Ал бұл айырма 7 ге бөлінеді.
болады. Ал бұл айырма 7 ге бөлінеді.
b) 7 -ге бөлінгіштіктің тағы да бір белгісін
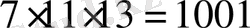 көбейтіндісінен пайдалану арқылы келтіріп шығаруға болады. Бөлінгіш сан төрт таңбалы сан немесе одан жоғары таңбалы сан болса ғана осы белгіні пайдалануға болады. Мұнда 1001 санының сиқырынан пайдаланылады. Кез келген үш таңбалы санды 1001 санына көбейтсек, сол үш таңбалы санды екі рет жазып (алты таңбалы сан түрінде) қоя салуға болады. Мысалы 859∙1001=859∙7∙11∙13= 859859; 658∙1001=658∙7∙11∙13 =658658.
көбейтіндісінен пайдалану арқылы келтіріп шығаруға болады. Бөлінгіш сан төрт таңбалы сан немесе одан жоғары таңбалы сан болса ғана осы белгіні пайдалануға болады. Мұнда 1001 санының сиқырынан пайдаланылады. Кез келген үш таңбалы санды 1001 санына көбейтсек, сол үш таңбалы санды екі рет жазып (алты таңбалы сан түрінде) қоя салуға болады. Мысалы 859∙1001=859∙7∙11∙13= 859859; 658∙1001=658∙7∙11∙13 =658658.
1001 санының осындай сиқырынан пайдаланып 7-ге бөлінгіштік белгісін келтіріп шығаруға болады. Соған мысал келтіреміз.
8-мысал Мысалы, 859 516 санының 7-ге бөлінетінін 1001 санының сиқырынан пайдаланып тексерейік. Берілген 859516 санын мынадай түрлендірейік: 859∙1001=859∙7∙11∙13= 859859; екендігінен пайдалансақ 859516=859∙1001-859+516=859859-343 түрінде жазуға болады. Соңғы теңдікте азайғыш 1001 ге (сәйкесінше, 7-ге де) бөлінеді, азайтқыш 343 тың 7-ге бөлінетінін тексеру жеткілікті. 343 = 49∙7, демек 859516 санының өзі де 7-ге бөлінеді.
с) Егер санның құрамындағы тақ орындағы цифрларының қосындысы мен оның жұп орындарындағы цифрларының қосындысының айырмасы нөлге тең немесе 7-ге бөлінетін болса, онда бұл сан 7-ге қалдықсыз бөлінеді.
9-мысал. 1) 85314507229 және 2) 363862625 сандарының 7 ге бөлінетінін тексерейік.
Шешу. 1) берілген санның соңынан үш-үштен шартты түрде бөліктерге бөлеміз. Бірінші және үшінді үштіктен, екінші және төртінші үштіктерден екі қосынды құрастырамыз:
 және
және
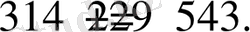 Олардың айырмасын табамыз
Олардың айырмасын табамыз
 бұл айырма 7 ге бөлінеді екен. Олай болса берілген санда 7 ге бөлінеді екен.
бұл айырма 7 ге бөлінеді екен. Олай болса берілген санда 7 ге бөлінеді екен.
2) жоғарыдағыдай үштіктерден пайдалансақ, айырма
625-862+363=126 ға тең болады, a) белгісіне сәйкес,
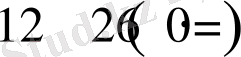 болса 7-ге бөлінеді, сондықтан 363862625 саны да 7-ге бөлінеді.
болса 7-ге бөлінеді, сондықтан 363862625 саны да 7-ге бөлінеді.
2. Натурал санның қарапайым жіктелуі
Айталық, а саны жай көбейткіштерге жіктелсін. Бұл жіктелудегі бірдей көбейткіштерді дәреже түрінде жазып, мынадай формула аламыз:
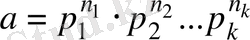 (1. 5. 1)
(1. 5. 1)
Мұнда p 1 , p 2 , . . . , р к - әp түрлі жай сандар, олар берілген а санының жай бөлгіштері деп аталады, п 1 , п 2 , . . . , п к - теріс емес бүтін сандар. Санның (1. 5. 1) түрінде жіктелуі оның қарапайым жіктелуі деп аталады. Мысалы,
1176 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 7 ∙ 7 = 2 3 ∙ 3 ∙ 7 2 .
Жалпы, санның карапайым жіктелуін табу (caн өте үлкен болғанда) күрделі әрі қиын жұмысқа айналады. Мысалы, ЭЕМ-ның көмегі арқылы 2 19937 -1 санының жай сан болатындығы жақында ғана анықталған және бұл санның жазылуына 60 000-нан астам цифр қажет болатындығы анықталған.
Дегенмен, өте үлкен емес сандардың қарапайым жіктелулерін анықтауға болады.
3. Арифметиканың негізгі теоремасы
Әрбір құрама санды жай сандардың көбейтіндісі ретінде жіктеп жазуға болады. Мысалы, 252=2 ∙ 2 ∙ 3 ∙ 3 ∙ 7 немесе 252=2 2 ∙ 3 2 ∙ 7. Бұл мысалдан кейбір жай сандар көбейткіш ретінде бірнеше рет қайталанатындығын көреміз.
Теорема . (Арифметиканың негізгі теоремасы) . 1-ден өзге әрбір натурал сан бір ғана түрде жай сандардың көбейтіндісіне жіктеледі.
4. Натурал сандардың бөлгіштер санын және бөлгіштерінің қосындысын анықтау
Кез келген күрделі
n
санын
 канондық жіктеуге болады. Мұндағы
канондық жіктеуге болады. Мұндағы
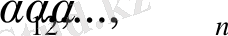 сандары
сандары
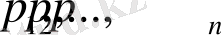 жай сандардың дәреже көрсеткіштері сол көбейткіштердің неше рет қатысатынын көрсетеді.
жай сандардың дәреже көрсеткіштері сол көбейткіштердің неше рет қатысатынын көрсетеді.
n
натурал санның барлық бөлгіштері санын
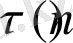 деп, барлық натурал бөлгіштерінің қосындысын
деп, барлық натурал бөлгіштерінің қосындысын
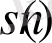 деп белгілейік.
деп белгілейік.
2 -теорема.
Егер
n
натурал санның канондық жіктелуі
 болса, онда
болса, онда
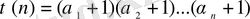 ,
,
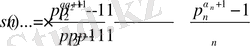 болады.
болады.
1-мысал.
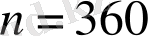 санның канондық жіктелуі
санның канондық жіктелуі
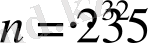 болғандықтан, оның натурал бөлгіштері саны
болғандықтан, оның натурал бөлгіштері саны
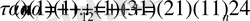 , ал осы әртүрлі натурал бөлгіштердің қосындысы
, ал осы әртүрлі натурал бөлгіштердің қосындысы
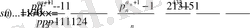 болады.
болады.
ЛЕКЦИЯ №2
Анықталмаған коэффициенттер әдісін қолданып теңдеулерді шешу.
Жоспар:
1. Горнер схемасы.
2. Безу теоремасы және анықталмаған коэффициенттер тәсiлi.
1 . Горнер схемасы.
1-Мысал.
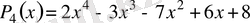 көпмүшелiгiн Безу теоремасы және Горнер схемасы әдiсiн пайдаланып көбейткiштерге жiктеу керек.
көпмүшелiгiн Безу теоремасы және Горнер схемасы әдiсiн пайдаланып көбейткiштерге жiктеу керек.
Шешуi: Көпмүшелiктiң коэффициенттерi бүтiн сандар, сондықтан
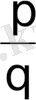 көпмүшелiктiң түбiрi болуы үшiн
көпмүшелiктiң түбiрi болуы үшiн
 саны 2-нiң натурал бөлгiштерi, яғни 1 мен 2,
саны 2-нiң натурал бөлгiштерi, яғни 1 мен 2,
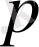 саны 8-дiң бүтін бөлгiштерi, яғни ±1, ±2, ±4, ±8 сандарының бiрi болуы керек.
саны 8-дiң бүтін бөлгiштерi, яғни ±1, ±2, ±4, ±8 сандарының бiрi болуы керек.
Сонымен есептiң рационал түбiрi болса
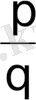 мына сандардың бiрi болуы керек: ±1, ±2, ±4, ±8, ±.
мына сандардың бiрi болуы керек: ±1, ±2, ±4, ±8, ±.
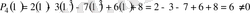
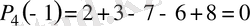 .
.
Сонымен берiлген көпмүшелiк
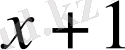 екiмүшелiгiне бөлiнедi екен.
екiмүшелiгiне бөлiнедi екен.
Горнер схемасымен бөлiндi көпмүшелiктi табайық:
x = -1
2 -3 -7 6 8
2 -5 -2 8 0

Сонда
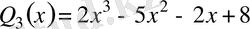 болады.
болады.
Бұл көпмүшелiктiң
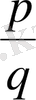 түбiрi болуы үшiн Р
4
(х) жағдайдағыдай, ол ±1, ±2, ±4, ±8, ± сандарының бiрi болуы керек.
түбiрi болуы үшiн Р
4
(х) жағдайдағыдай, ол ±1, ±2, ±4, ±8, ± сандарының бiрi болуы керек.
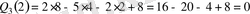 болғандықтан Q
3
(х) көп-мүшелiгi (х-2) екiмүшелiгiне бөлiнедi.
болғандықтан Q
3
(х) көп-мүшелiгi (х-2) екiмүшелiгiне бөлiнедi.
Горнер схемасы бойынша:
x = 2
2 -5 -2 8
2 -1 -4 0
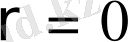
бөлiндi көпмүшелiк
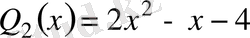 . Сонымен,
. Сонымен,
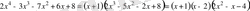
2-Мысал.
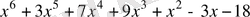 көпмүшелiгiн Безу теоремасы және Горнер схемасының жәрдемiмен көбейткiштерге жiктеу. Мұнда
көпмүшелiгiн Безу теоремасы және Горнер схемасының жәрдемiмен көбейткiштерге жiктеу. Мұнда
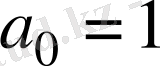 . Сондықтан көпмүшелiк-тiң рационал түбiрi 18-дiң бөлгiштерi болу керек. Ол,
. Сондықтан көпмүшелiк-тiң рационал түбiрi 18-дiң бөлгiштерi болу керек. Ол,
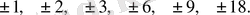 Ал,
Ал,
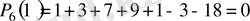
болғандықтан берiлген көпмүшелiк
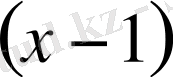 -ге бөлiнедi. Горнер схемасы бойынша:
-ге бөлiнедi. Горнер схемасы бойынша:
x = 1
1 3 7 9 1 -3 18
1 4 11 20 21 18 0
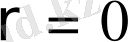
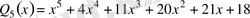 .
.
Мұнда
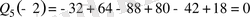
Сондықтан
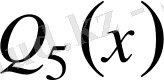 көпмүшелiгi
көпмүшелiгi
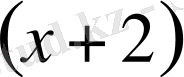 - ге бөлiнедi.
- ге бөлiнедi.
Горнер схемасы бойынша:
x = -2
1 4 11 20 21 18 18
1 2 7 6 9 0
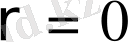

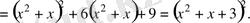
Сонымен,
 .
.
2. Безу теоремасы және анықталмаған коэффициенттер тәсiлi.
3-Мысал.
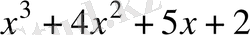 көпмүшелiгiн Безу теоремасы және анықталмаған коэффициенттер әдiсiмен көбейткiштерге жiктеңдер.
көпмүшелiгiн Безу теоремасы және анықталмаған коэффициенттер әдiсiмен көбейткiштерге жiктеңдер.
Шешуі:Көпмүшелiктiң рационал түбiрi
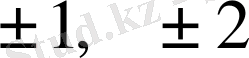 бiрi болу керек.
бiрi болу керек.
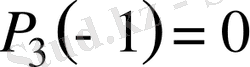 болғандықтан
болғандықтан
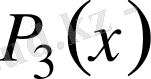 көпмүшелiгi
көпмүшелiгi
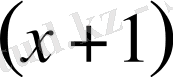 - ге бөлiнедi.
- ге бөлiнедi.
Анықталмаған коэффициенттер әдiсiмен
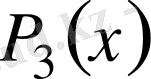 көпмүшелi-гiн
көпмүшелi-гiн
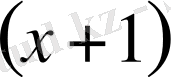 -ге бөлгенде шығатын көпмүшелiктi табайық, ол
-ге бөлгенде шығатын көпмүшелiктi табайық, ол
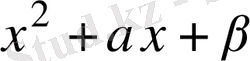 дейiк. Сонда
дейiк. Сонда
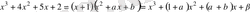 болады. Мұндағы тең дәрежелi
болады. Мұндағы тең дәрежелi
 -тың коэффициенттерiн теңестiрсек:
-тың коэффициенттерiн теңестiрсек:
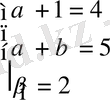
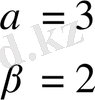
Сондықтан
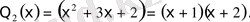
Сонымен
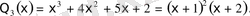
ЛЕКЦИЯ№3 . Теңсiздiктердi дәлелдеу. Иррационал теңдеулер мен теңсіздіктерді шешу әдістері. Қиындатылған есептер.
ЖОСПАР:
1. Теңсіздіктердің қасиеттері
2. Теңсіздіктерді дәлелдеу
3. Қиындатылған есептер
1. Теңсіздіктердің қасиеттері
Нақты сандар өрісінің тәртіптілік қасиеті бар: кез келген екі нақты санның бірі екіншісінен не үлкен, не тең, не кіші болады. Бұл қатыстарды
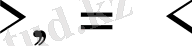 таңбаларымен белгілейді. Сонда
таңбаларымен белгілейді. Сонда
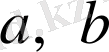 нақты сандар болса, онда олар арасында мына қатыстың
нақты сандар болса, онда олар арасында мына қатыстың
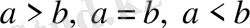 тек бірі орындалады.
тек бірі орындалады.
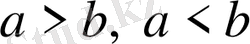 қатыстарын теңсіздіктер дейді.
қатыстарын теңсіздіктер дейді.
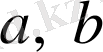 ол теңсіздіктің мүшелері делінеді
ол теңсіздіктің мүшелері делінеді
 деген
деген
 мен
мен
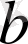 -ның айырмасы оң сан,
-ның айырмасы оң сан,
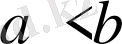 деген
деген
 мен
мен
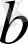 -ның айырымы теріс сан деген сөз.
-ның айырымы теріс сан деген сөз.
 мен
мен
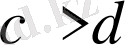 теңсіздіктерін бір мағыналы, ал
теңсіздіктерін бір мағыналы, ал
 мен
мен
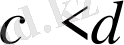 теңсіздіктерін қарама қарсы мағыналы теңсіздіктер дейді. Олар қатаң теңсіздіктер. Олармен қатар қатаң емес
теңсіздіктерін қарама қарсы мағыналы теңсіздіктер дейді. Олар қатаң теңсіздіктер. Олармен қатар қатаң емес
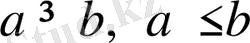 теңсіздіктер қарастырылады.
теңсіздіктер қарастырылады.
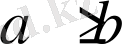 теңсіздігі
теңсіздігі
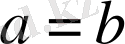 болғанда да,
болғанда да,
 болғанда да дұрыс, ал
болғанда да дұрыс, ал
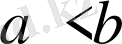 болғанда дұрыс емес
болғанда дұрыс емес
 ,
,
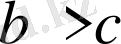 екі теңсіздіктің орнына
екі теңсіздіктің орнына
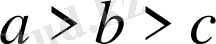 немесе
немесе
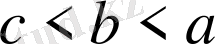 қос теңсіздігін пайдалануға болады.
қос теңсіздігін пайдалануға болады.
Сандық теңсіздіктердің мынадай түрлері бар:
- Егерболса, ондаболады. Бұл теңсіздіктің қайтымсыздық қасиеті.
- Егерболса, онда кез-келген с үшінболады.
- Егерболса, ондаболады (Бұл теңсіздіктің транзитивтік қасиеті) .
- Егерболса, ондаболады.
- Егерболса, ондаболады.
Егер
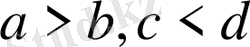 болса, онда
болса, онда
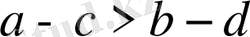 болады.
болады.
- Егерболса онда кез-.
- Егерболса, ондаболады.
- Егерболса, ондаболады.
- Егерболса, онда кез-келген натурал санүшінболады. , ондаболады.
- Егерболса, онда кез-келген натурал сан n үшінболады.
- Егерболса, онда кез-келген натурал сан n үшінболады.
- Егерболса, онда кез-келген натурал сан n үшінболады.
Сан модуліне арналған кейбір теңсіздіктерді дәлелдейік.
- Кез келгенсаны үшінболады
Дәлелдеуі:
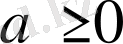 болса, онда
болса, онда
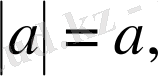 ал
ал
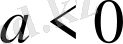 болса онда
болса онда
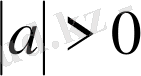 болғандықтан
болғандықтан
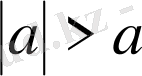 қатаң теңсіздігі орындалады. Сонымен
қатаң теңсіздігі орындалады. Сонымен
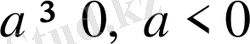 екі жағдай үшін
екі жағдай үшін
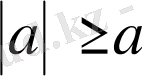 болады.
болады.
- Кез-келгенжәнесандары үшінболады.
Дәлелдеуі: 13 бойынша
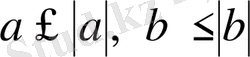 болады оларды қоссақ 5 қасиет бойынша:
болады оларды қоссақ 5 қасиет бойынша:
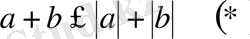 болып шығады. Ал
болып шығады. Ал
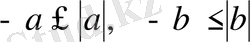 болғандықтан қоссақ
болғандықтан қоссақ
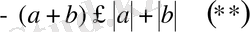 . Сонда
. Сонда
 мен
мен
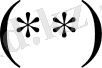 -ден
-ден
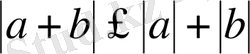 болады. Мұндағы теңдік
болады. Мұндағы теңдік
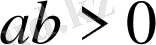 болғанда орын алады.
болғанда орын алады.
- Кез-келгенменсандары үшінболады. Дәлелдеуі:болады.
Бұған 14 пайдалансақ:
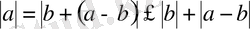 , бұдан
, бұдан
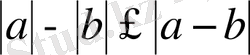 .
.
Екі нақты саны өзара салыстыру үшін түрлі әдістер қолданылады.
- Егер екі бүтін сан берілсе, онда олардың қайсысының екіншісінен үлкен не кіші екенін ажырату тікелей анықталады.
- Екі бөлшек санды салыстыру үшін, олардың не алымдарын не бөлімдерін бірдей күйге келтіру керек. .
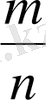 және
және
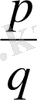 бөлшектерін ортақ бөлімге
бөлшектерін ортақ бөлімге
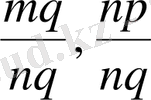 келтірсек және
келтірсек және
 болса, онда
болса, онда
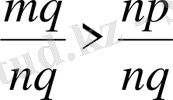 болар еді де, қысқартқаннан соң
болар еді де, қысқартқаннан соң
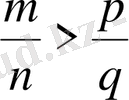 болып шығады.
болып шығады.
1-Мысал.
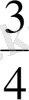 және
және
 бөлшектерін салыстыру үшін, ортақ бөлімге келтіреміз
бөлшектерін салыстыру үшін, ортақ бөлімге келтіреміз
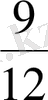 және
және
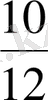 .
.
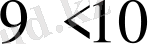 болғандықтан
болғандықтан
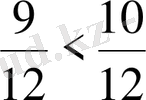 , бұдан
, бұдан
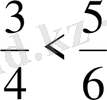 болады.
болады.
3. Түбірлерді (радикалдарды) салыстыру үшін, түбірлердің дәрежесін теңестіріп, түбір астындағы санды салыстыру керек.
Мәселен,
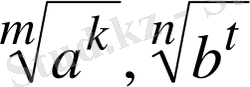 болса мына
болса мына
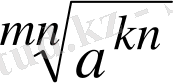 және
және
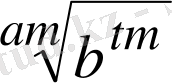 күйге келтіріп
күйге келтіріп
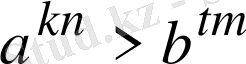 болса, онда
болса, онда
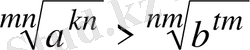 болады да,
болады да,
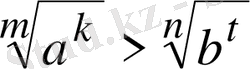 болып шығады.
болып шығады.
2-Мысал.
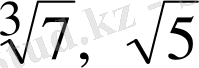 түбірлерін салыстыру үшін, түбір дәрежелерін, тең күйге келтіреміз. Сонда
түбірлерін салыстыру үшін, түбір дәрежелерін, тең күйге келтіреміз. Сонда
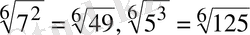 болып
болып
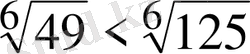 болғандықтан
болғандықтан
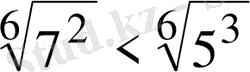 , бұдан
, бұдан
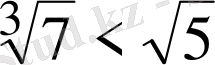 болып шығады.
болып шығады.
- Логарифімді салыстырғанда мыналарды ескерту керк:
а)
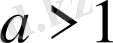 болғанда, егер
болғанда, егер
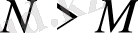 болса,
болса,
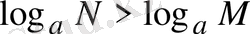 болады.
болады.
б)
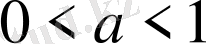 болғанда егер
болғанда егер
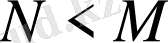 болса
болса
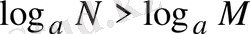 болады.
болады.
3-Мысал.
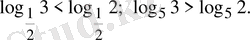
Бірінші теңсіздікте
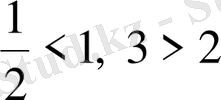 , екінші теңсіздікте
, екінші теңсіздікте
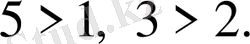
4-Мысал.
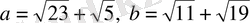 . Егер
. Егер
 деп жорысақ, онда
деп жорысақ, онда
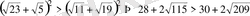 болар еді. Түрлендірсек
болар еді. Түрлендірсек
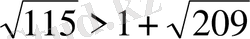 болар еді.
болар еді.
Бұл теңсіздік дұрыс емес, сондықтан
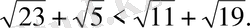 дәл осы есепті былайша да салыстыруға болады, әр түбірді жеке-жеке бағалаймыз:
дәл осы есепті былайша да салыстыруға болады, әр түбірді жеке-жеке бағалаймыз:
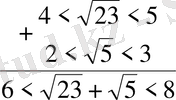
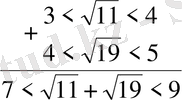
Бұдан қай түбірлер қосынндысының үлкен екендігі байқалмайды. Өйткені 6 мен 8-дің арасында жатқан сан 7 мен 9-дың арасында жатқан саннан кіші болады деуге болмайды. Мәселен, бірінші 7, 9 екіншісі 7, 5 болуы мүмкін. Сондықтан, енді ол қосылғыштарды 0, 1дәлдікте бағалаймыз.
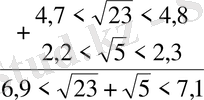
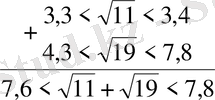
Бұдан екінші қосылғыштың көп екені көрінеді, оның аз мәнінің өзі бірінші қосылғыштың артығымен алынған мәнінен көп болып кетті: Сонымен
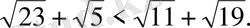
5-Мысал.
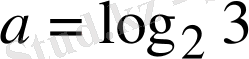 және
және
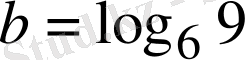 сандарын салыстыру керек:
сандарын салыстыру керек:
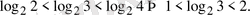
Ал,
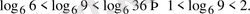
Сонымен
 мен
мен
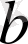
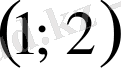 аралықта жатыр екен
аралықта жатыр екен
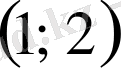 аралықтың қақ ортасы
аралықтың қақ ортасы
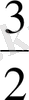 . Берілген сандар
. Берілген сандар
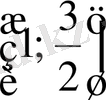 немесе
немесе
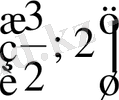 аралықтың қайсысында жататынын анықтаймыз:
аралықтың қайсысында жататынын анықтаймыз:
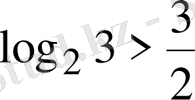 дейік, онда
дейік, онда
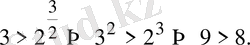
Бұл теңсіздік дұрыс. Сондықтан
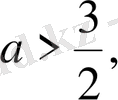 яғни
яғни
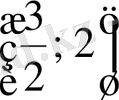 аралықта жатады екен. Енді
аралықта жатады екен. Енді
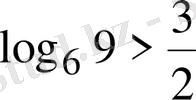 дейік, онда
дейік, онда
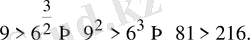 Бұл дұрыс емес теңсіздік. Сондықтан
Бұл дұрыс емес теңсіздік. Сондықтан
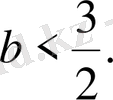 Сонымен
Сонымен
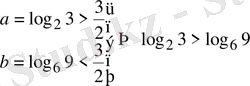 болып шығады.
болып шығады.
6-Мысал.
 және
және
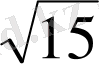 сандарын салыстыру:
сандарын салыстыру:
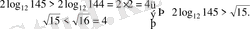
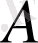 және
және
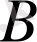 алгебралық өрнектің мүмкін мәндері облысына кіретін
алгебралық өрнектің мүмкін мәндері облысына кіретін
 жиынынан алынған сандарға сай келетін
жиынынан алынған сандарға сай келетін
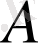 өрнегінің сан мәні сол сандарға сай келетін
өрнегінің сан мәні сол сандарға сай келетін
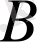 өрнегінің сан мәнінен үлкен (кіші) болатын болса,
өрнегінің сан мәнінен үлкен (кіші) болатын болса,
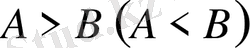 теңсіздігі
теңсіздігі
 жиынында теңбе тең теңсіздік делінеді.
жиынында теңбе тең теңсіздік делінеді.
Мысалы:
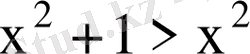 теңсіздігі нақты сандар жиынында теңбе-тең теңсіздік болады, өйткені
теңсіздігі нақты сандар жиынында теңбе-тең теңсіздік болады, өйткені
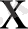 -тың кез-келген нақты мәнінде бұл теңсіздік дұрыс теңсіздік.
-тың кез-келген нақты мәнінде бұл теңсіздік дұрыс теңсіздік.
Егер
 жиыны берілмесе, онда теңбе тең теңсіздік ол теңсіздікке кіретін өрнектердегі мүмкін мәндері жиынында қаратырылады.
жиыны берілмесе, онда теңбе тең теңсіздік ол теңсіздікке кіретін өрнектердегі мүмкін мәндері жиынында қаратырылады.
Алгебралық өрнектерде де қатаң теңсіздіктермен
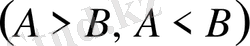 қатар, қатаң емес теңсіздіктер
қатар, қатаң емес теңсіздіктер
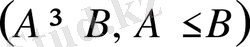 қарастырылады. Қатаң емес
қарастырылады. Қатаң емес
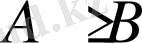 теңсіздікте бұл өрнектердің мұмкін мәндері облысына кіретін
теңсіздікте бұл өрнектердің мұмкін мәндері облысына кіретін
 жиынынан алынған сандарға сай келетін
жиынынан алынған сандарға сай келетін
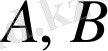 өрнектерінің сан мәндері не тең, не
өрнектерінің сан мәндері не тең, не
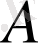 -ның сан мәні
-ның сан мәні
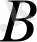 -ның сан мәнінен үлкен деп түсіну керек.
-ның сан мәнінен үлкен деп түсіну керек.
2. Теңсіздіктерді дәлелдеу
Теңбе-тең теңсіздіктердің мынадай қасиеттері бар:
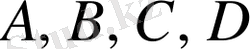 алгебралық өрнектерінің мүмкін мәндері облысынан алынған
алгебралық өрнектерінің мүмкін мәндері облысынан алынған
 жиынында:
жиынында:
- болса, ондаболады.
- болса, ондаболады. .
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады, -натурал сан.
- болса, ондаболады, - натурал сан.
- болса, ондаболады, - натурал сан.
- болса, ондаболады, - натурал сан.
- болса, ондаболады, - натурал сан.
- болса, ондаболады, - натурал сан.
Бұл келтірілген қасиеттер
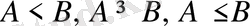 теңсіздіктері үшін де дұрыс. Көптеген жағдайда теңсіздіктердің берілген жиынында немесе ол теңсіздіктерге кіретін алгебралық өрнектердің мүмкін мәндері жиыны облысында теңсіздіктердің дұрыс, не қате екенін дәлелдеуге тура келеді.
теңсіздіктері үшін де дұрыс. Көптеген жағдайда теңсіздіктердің берілген жиынында немесе ол теңсіздіктерге кіретін алгебралық өрнектердің мүмкін мәндері жиыны облысында теңсіздіктердің дұрыс, не қате екенін дәлелдеуге тура келеді.
Дәлелдеу түрлі жолмен іске асады. Ол жолдардың кейбіреулеріне мысал келтірейік.
2. 1 Теңсіздікті оның анықтамасына сүйеніп дәлелдеу.
Теңсіздіктің анықтамасы бойынша
 болу үшін
болу үшін
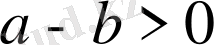 болуы жеткілікті. Сондықтан
болуы жеткілікті. Сондықтан
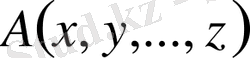 және
және
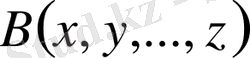 алгебралық өрнектері үшін
алгебралық өрнектері үшін
 екенін көрсету үшін
екенін көрсету үшін
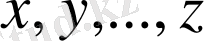 айнымалылардың қарастырылып отырған жиыннан алынатын кез-келген сан мәндері үшін
айнымалылардың қарастырылып отырған жиыннан алынатын кез-келген сан мәндері үшін
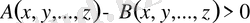 екенін дәлелдеу керек.
екенін дәлелдеу керек.
1-Мысал. Таңбалас кез-келген екі нақты санның бір-біріне қатынастарының қосындысы 2-ден кем болмайтындығын, яғни
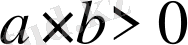 болса, онда
болса, онда
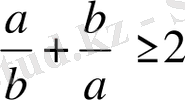 болатындығын дәлелдеу керек.
болатындығын дәлелдеу керек.
Дәлелдеуі: Мына айырымды қарастырамыз.
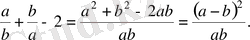
Бұл өрнек
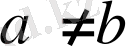 болса оң, ал
болса оң, ал
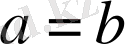 болса нөлге тең. Сондықтан
болса нөлге тең. Сондықтан
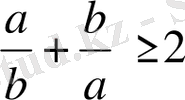 дұрыс теңсіздік.
дұрыс теңсіздік.
2-Мысал. Екі оң нақты санның арифметикалық ортасы, сол сандардың геометриялық ортасынан кем болмайды, Яғни
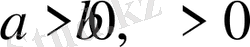 болса, онда
болса, онда
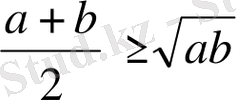 болады. (Коши теңсіздігі) .
болады. (Коши теңсіздігі) .
Дәлелдеуі: Айырымын қарастырамыз.
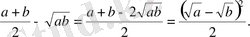
Соңғы өрнек кез-келген
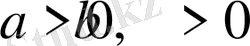 сандары үші оң, ал
сандары үші оң, ал
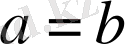 болса нөл. Сондықтан
болса нөл. Сондықтан
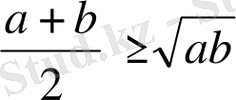 теңсіздік дұрыс.
теңсіздік дұрыс.
3-Мысал. Оң сан үшін
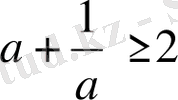 болатындығын дәлелдеу керек.
болатындығын дәлелдеу керек.
Дәлелдеуі: Айырымы
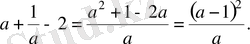
Бұл кез келген
 оң сан үшін. Сондықтан
оң сан үшін. Сондықтан
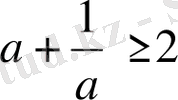 теңсіздік дұрыс. Тепе-теңдік тек
теңсіздік дұрыс. Тепе-теңдік тек
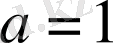 болғанда орындалады.
болғанда орындалады.
4-Мысал.
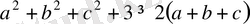 теңсіздігін дәлелдеңіздер.
теңсіздігін дәлелдеңіздер.
Дәлелдеуі: Айырымы
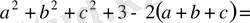
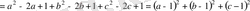
Кез-келген нақты сан
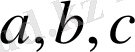 үшін оң сан болады. Сондықтан,
үшін оң сан болады. Сондықтан,
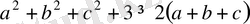 дұрыс теңсіздік.
дұрыс теңсіздік.
5-Мысал. Кез-келген оң сандар үшін
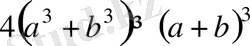 теңсіздігінің дұрыстығын дәлелдеңіздер.
теңсіздігінің дұрыстығын дәлелдеңіздер.
Дәлелдеуі: Айырымы
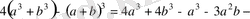
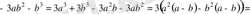
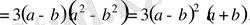
Бұл кез-келген
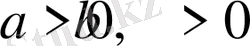 үшін оң сан. Сондықтан берілген теңсіздік дұрыс.
үшін оң сан. Сондықтан берілген теңсіздік дұрыс.
6-Мысал.
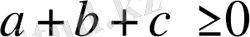 болғанда,
болғанда,
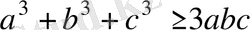 болатынын дәлелдеңіздер.
болатынын дәлелдеңіздер.
Дәлелдеуі: Айырымы
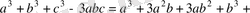
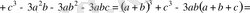
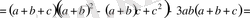
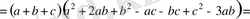
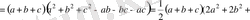
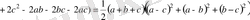
Есептің шарты бойынша
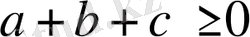 болғандықтан бұл өрнек оң (теңдік
болғандықтан бұл өрнек оң (теңдік
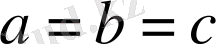 болғанда орындалады) Сондықтан берілген теңсіздік дұрыс.
болғанда орындалады) Сондықтан берілген теңсіздік дұрыс.
7-Мысал. Кез-келген
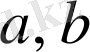 сандары үшін
сандары үшін
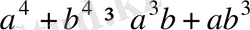 теңсіздігінің дұрыстығын дәлелдеңіздер.
теңсіздігінің дұрыстығын дәлелдеңіздер.
Дәлелдеуі: Айырымы
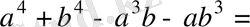
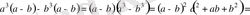
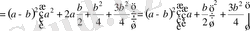
кез келген
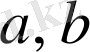 үшін оң сан,
үшін оң сан,
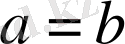 үшін нөл болады. Сондықтан берілген теңсіздік дұрыс.
үшін нөл болады. Сондықтан берілген теңсіздік дұрыс.
2. 2 Теңсіздікті дәлелдеудің синтетикалық әдісі.
Бұл әдіс бойынша, бірқатар түрлендірулер арқылы дәлелденбек теңсіздікті, дұрыстығы дәлелденген немесе талас тудырмайтын шүбәсіз теңсіздіктерге алып келіп, солар арқылы дәлелдейді. Ондай теңсіздіктерді тірек теңсіздіктер дейді.
Оларға жататындар:
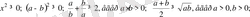
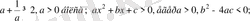
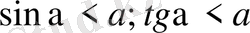 т. б. теңсіздіктер.
т. б. теңсіздіктер.
8-Мысал.
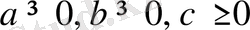 болғанда,
болғанда,
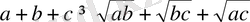 болатынын дәлелдеу керек.
болатынын дәлелдеу керек.
Дәлелдеуі: Тірек теңсіздік үшін Коши теңсіздігін пайдаланайық. Сонда
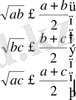 болғандықтан, оларды мүшелеп қоссақ
болғандықтан, оларды мүшелеп қоссақ
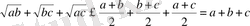 болып шығады. Демек, берілген теңсіздік дұрыс.
болып шығады. Демек, берілген теңсіздік дұрыс.
9-Мысал. Оң сандар үшін
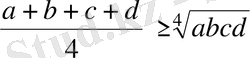
 болатынын дәлелдеңіздер.
болатынын дәлелдеңіздер.
Дәлелдеуі: Коши теңсіздігін екі рет пайдаланамыз. Сонда
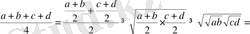
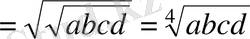 болып теңсіздік дәлелденеді.
болып теңсіздік дәлелденеді.
10-Мысал.
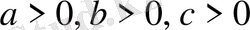 болғанда
болғанда
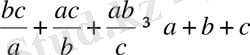 болатынын дәлелдеңіздер.
болатынын дәлелдеңіздер.
Дәлелдеуі:
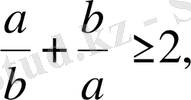
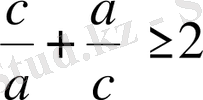 ,
,
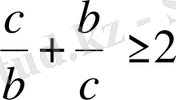 болғандықтан
болғандықтан
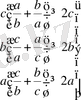 болар еді. Бұдан,
болар еді. Бұдан,
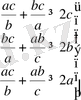 болады.
болады.
Мүшелеп қоссақ,
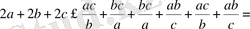
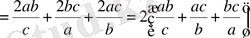 немесе
немесе
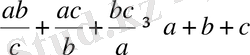 .
.
11-Мысал.
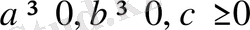 болғанда
болғанда
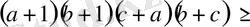
 болатынын дәлелдеңіздер.
болатынын дәлелдеңіздер.
Дәлелдеуі:
 ⇒
⇒
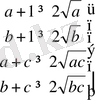 ⇒
⇒
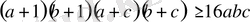
12-Мысал. Кез келген натурал n үшін
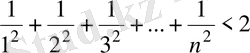 болатынын дәлелдеңіздер.
болатынын дәлелдеңіздер.
Дәлелдеуі: кез келген натурал сан
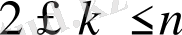 үшін мына теңсіздік
үшін мына теңсіздік
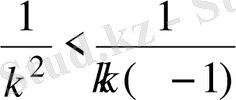 болатындықтан
болатындықтан
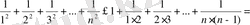
=
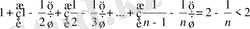 болып шығады.
болып шығады.
13-Мысал. Теңсіздікті дәлелдеңіздер:
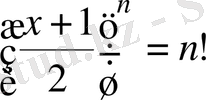
Мұндағы
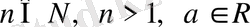
Дәлелдеуі: Коши теңсіздігін пайдаланамыз.
 бұларды көбейтсек.
бұларды көбейтсек.
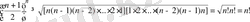
14-Мысал. Кез-келген нақты сан үшін
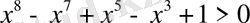 дұрыстығын дәлелдеңіздер.
дұрыстығын дәлелдеңіздер.
Дәлелдеуі. Сан осін
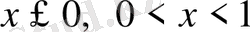 және
және
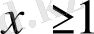 аралықтарға бөліп, сол аралықта берілген теңсіздікті қарастырайық.
аралықтарға бөліп, сол аралықта берілген теңсіздікті қарастырайық.
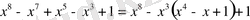
а)
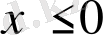 аралықта
аралықта
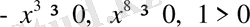 ал
ал
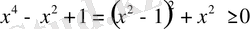 болғандықтан, бұл аралықта
болғандықтан, бұл аралықта
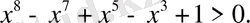
б)
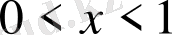 аралықта
аралықта
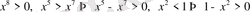
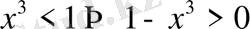 болғандықтан
болғандықтан
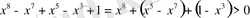 .
.
в)
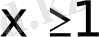 аралықты қарасатырайық. Бұл кезде
аралықты қарасатырайық. Бұл кезде
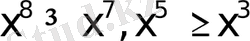 болатындықтан
болатындықтан
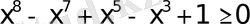 болып шығады. Сонымен үш аралықта да оң сан болатындықтан теңсіздік дұрыс.
болып шығады. Сонымен үш аралықта да оң сан болатындықтан теңсіздік дұрыс.
2. 3. Қарсы жору арқылы дәлелдеу.
15-Мысал.
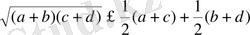 болатынын дәлелдеңіздер.
болатынын дәлелдеңіздер.
Дәлелдеуі: а, в, с, д-лардың кебір мәндеріне теңсіздік дұыс емес дейік, онда
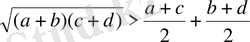 орындалады. Екі жағын квадраттайық (олар сан өрнек)
орындалады. Екі жағын квадраттайық (олар сан өрнек)
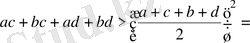
=
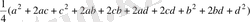 .
.
Бұдан
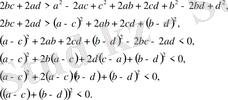
Бұл теңсіздік дұрыс емес сондықтан берілген теңсіздік дұрыс.
16-Мысал.
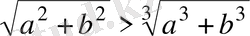 теңсiздiгiн дәлелдеңiздер. Дәлелдеуi.
теңсiздiгiн дәлелдеңiздер. Дәлелдеуi.
 мен
мен
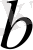 -ны» кейбiр мәндерiнде бұл дұрыс емес десек, онда
-ны» кейбiр мәндерiнде бұл дұрыс емес десек, онда
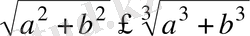 өрнегi дұрыс болады. Бұдан
өрнегi дұрыс болады. Бұдан
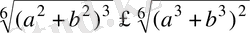 оң болғандықтан,
оң болғандықтан,
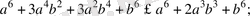
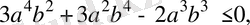
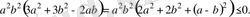
Бұл терiс болуы мүмкiн емес және тек
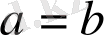 болғанда нөлге тең. Сондықтан берiлген теңсiздiк дұрыс.
болғанда нөлге тең. Сондықтан берiлген теңсiздiк дұрыс.
2. 4. Математика индукция әдісімен теңсіздіктерді дәлелдеу.
Бір теңсіздіктің кез келген натурал сан үшін дұрыс екендігін дәлелдеу керек болсын . Ол теңсіздіктің барлық натурал сандар үшін дұрыстығын жеке-жеке тексеріп шығу мүмкін емес. Сондықтан ол теңсіздіктің
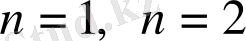 болған кезде дұрыстығын тексереді де, ол теңсіздікті
болған кезде дұрыстығын тексереді де, ол теңсіздікті
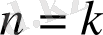 болғанда дұрыс деп алады да,
болғанда дұрыс деп алады да,
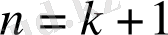 болғанда дұрыс екенін дәлелдейді. Сонда дұрыс болып шықса, онда
болғанда дұрыс екенін дәлелдейді. Сонда дұрыс болып шықса, онда
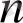 үшін де дұрыс болады.
үшін де дұрыс болады.
17-Мысал. Кез келген натурал сан үшін
 болатынын дәлелдеңіздер
болатынын дәлелдеңіздер
Дәлелдеуі.
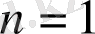 болғанда
болғанда
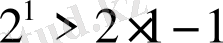 теңсіздік дұрыс
теңсіздік дұрыс
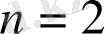 болғанда
болғанда
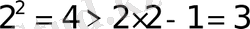 теңсіздік дұрыс
теңсіздік дұрыс
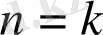 болғанда, теңсіздік
болғанда, теңсіздік
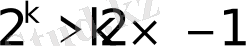
 дұрыс дейік те
дұрыс дейік те
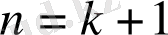 болғанда да дұрыстығын дәлелдейік, яғни
болғанда да дұрыстығын дәлелдейік, яғни
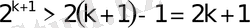 -дің дұрыстығын дәлелдейік
-дің дұрыстығын дәлелдейік
 ескерсек,
ескерсек,
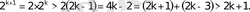
Сонымен теңсіздік
 болғанда да дұрсы болады. Сондықтан берілген теңсіздік
болғанда да дұрсы болады. Сондықтан берілген теңсіздік
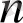 -нiң кез келген мәнінде дұрыс болады.
-нiң кез келген мәнінде дұрыс болады.
18-Мысал. Бернулли теңсіздігінің
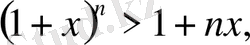 мұндағы
мұндағы
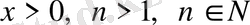 дұрыстығын дәлелдеңіздәр.
дұрыстығын дәлелдеңіздәр.
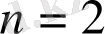 болса
болса
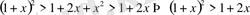
Теңсіздік
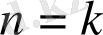 болғанда дұрыс болсын, яғни
болғанда дұрыс болсын, яғни
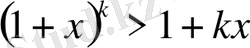 болсын.
болсын.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz