Мектеп геометриясында векторлық әдісті оқытудың теориясы мен әдістемесі


Мектеп оқушыларын векторлық әдіске оқытудың теориясы мен әдістемесі
Мазмұны
Кіріспе
1 тарау. Мектеп геометрия курсында векторлық әдісті зерттеудің теориялық және әдістемелік ерекшеліктері
1. 1 Аналитикалық әдістердің пайда болу және қалыптасу тарихы
1. 2 Математика мен мектеп математика курсында вектор ұғымын анықтаудың әртүрлі тәсілдері
1. 3 Психологиялық және әдістемелік проблема ретінде есептерді шешуге үйрету
1. 4 Геометриядағы аффиндік есептерді шешудің векторлық әдісін оқыту әдістемесі
2 тарау. 10-сыныпта «Кеңістіктегі векторлар» тақырыбын зерттеу әдістемесі
2. 1 10-сыныптағы «Кеңістіктегі векторлар» тақырыбына логикалық-дидактикалық талдау
2. 2 Геометриялық есептерді шешуде векторлық әдісті қолдану әдістемесі
2. 3 Мазмұнды геометриялық есептерді шешудің векторлық әдісін оқыту әдістемесі
2. 4 Тәжірибелік жұмыстың сипаттамасы
Қорытынды
Әдебиеттер тізімі
Қосымшалар
Кіріспе
Өзектілігі. ҚР білімінің тұжырымдамасына сәйкес, атап айтқанда, математикалық тұрғыдан алғанда, орта мектепте оқушыларды оқыту, дамыту және тәрбиелеу міндеттерінің бірі білім берудің келесі екі негізгі мақсатына қол жеткізу болып табылады: тез өзгеретін өмір жағдайларына бейімделе алатын және сол жағдайларды бір уақытта өзгерте алатын адамды тәрбиелеу. Тиісінше, мектептің күш-жігері екі бағытта шоғырлануы керек: зияткерлікті дамыту үшін жағдай жасау және оқушылардың жеке басының шығармашылық қасиеттерін қалыптастыру.
Бөлінген бағыттар шеңберінде математикалық білім берудің басым мақсаттарының бірі «математика туралы ғылымның әмбебап тілі, құбылыстар мен процестерді модельдеу құралы, математиканың идеялары мен әдістері туралы түсініктерді қалыптастыру» болып табылады [23, 3 б. ] .
Векторлық әдіс - геометрияның негізгі әдістерінің бірі. Оның көмегімен планиметрия мен стереометрияның бірқатар аффиндік және метрикалық есептерін, физика мен астрономияның бірқатар қолданбалы мәселелерін тиімді шешуге болады.
Сондай-ақ, векторлық әдісті зерттеу тәуелсіз танымдық қызығушылық болып табылады, өйткені оның негізінде жазықтықтағы және кеңістіктегі координаттар әдісін дұрыс енгізіледі.
Айта кету керек, мектеп математика курсында «векторлар» тақырыбы және онымен бірге векторлық әдіс салыстырмалы түрде жақында, өткен ғасырдың алпысыншы жылдарының басында пайда болды. Алайда, бірден вектор ұғымы мектептегі математика курсының жетекші ұғымдарының біріне айналды, ал векторлық әдіс есептерді шешудің және теоремаларды дәлелдеудің негізгі әдістерінің бірі болды.
Кез-келген мектеп оқулығында «векторлар» тақырыбының көрінісі екі кезеңнен тұрады: векторлар мен векторлық әдісті зерттеу 1) планиметрияда; 2) стереометрияда.
«Кеңістіктегі векторлар» тақырыбын зерттеу оқушыларға адам қызметінің әртүрлі салаларында векторларды қолданудың кеңдігі туралы түсінік алуға, векторлық есептеулерді дамытудың кейбір фактілерімен танысуға, кеңістіктегі векторлар туралы жүйелі ақпаратты игеруге, векторлардың жазықтық және кеңістіктік арасындағы ұқсастықты көрсетіп үйренуге, есептерді шешуде жазықтық және кеңістіктік формаларды зерттеу үшін векторлық әдісті қолдануға мүмкіндік береді.
«Векторлар. Есептерді шешудің векторлық әдісі» тақырыбын зерттеуді әр түрлі кезеңдерде көптеген физиктер, математиктер және әдіскерлер айналысты (К. Вессель, Р. Декарт, Ж. Арган, З. А. Скопец, А. Н. Колмогоров, А. Д. Александров, В. А Гусев, Ю. М Калягин. ) . Қазіргі уақытта вектор ұғымын анықтауға бірнеше тәсілдер бар, векторларға қолданылатын амалдар, векторлық әдіспен шешілетін мәселелер шеңбері және векторлық әдісті қолдану анықталған. Оқушыларды векторларға, атап айтқанда векторлық әдіске оқытудың жеке әдістері жасалды. Олардың барлығы векторлардың негізгі мақсаты - геометриялық есептерді шешу үшін алгебралық заңдылықтарды қолдану идеясына негізделген.
Осыған қарамастан, көптеген сарапшылар, кейбір мұғалімдер, оқушылар мазмұнды есептерді шешуде векторлық әдісті қолдану қиынға соғатынын айтады.
Жоғарыда айтылғандар оқушыларға геометриялық есептерді шешудің векторлық әдісін үйрету қажеттілігі мен іс жүзінде оған жеткіліксіз назар аудару арасындағы қайшылықты бөліп көрсетуге мүмкіндік береді. Бұл қарама-қайшылықты шешу әсіресе стреометрияда векторлар арқылы шешілетін мәселелер ауқымы 10-сыныпта «Кеңістіктегі векторлар» тақырыбын зерттеуде өте маңызды, өйткені «Математиканы оқыту теориясы мен әдістемесінде» жазықтықта векторлық әдісті зерттеуге арналған ұсыныстар берілген.
Осылайша, жоғарыда келтірілген қарама-қайшылық жұмыстың өзектілігін анықтайды, ол оқушыларға «кеңістіктегі векторлар» тақырыбындағы геометриялық есептерді шешудің векторлық әдісін үйрету бойынша негізделген әдістемелік ұсыныстарды әзірлеу арқылы шешуден тұрады.
Зерттеудің мақсаты - геометриялық есептерді шешудің векторлық әдісін зерттеудің теориялық және әдістемелік жағдайларын анықтау және оқушыларды осы әдіске үйрету үшін ғылыми негізделген әдістемелік ұсыныстар жасау.
Зерттеу нысаны - жалпы білім беретін мектептің жоғары сыныптарында геометрияны оқыту процесі;
Зерттеу пәні - оқушыларды есептерді шешудің векторлық әдісіне оқытудың әдістемелік жүйесі.
Зерттеу гипотезасы: егер біз оқушыларға векторлық әдіске үйретуді құрайтын дағдылар мен іс-әрекеттерді мақсатты түрде үйретсек, жеке эвристикалық мәселелердің жекелеген түрлерін шешуге тұжырымдайтын болсақ, онда бұл оқушылардың осы әдісті тиімді игеруіне ықпал етеді.
Қойылған мақсатқа жету және гипотезаны тексеру үшін келесі мәселелерді шешу қажет болды:
1. Оқушылардың геометриялық есептерді шешудің векторлық әдісін сәтті меңгеру жағдайларын анықтау үшін зерттеу мәселесі бойынша психологиялық-педагогикалық және ғылыми-әдістемелік әдебиеттерге талдау жүргізу;
2. «Кеңістіктегі векторлар» тақырыбы бойынша бағдарламалық құжаттарға, мектеп оқулықтарына талдау жүргізу;
3. Мектеп геометрия курсында есептерді шешудің векторлық әдісін зерттеуге арналған әдістемелік ұсыныстар жасауға болатын теориялық және әдістемелік тұжырымдаманы анықтау;
4. Оқушылардың векторлық әдісті сәтті игеруі үшін әдістемелік ұсыныстар әзірлеу;
5. Әзірленген әдістемелік ұсынымдарға тәжірибелік тексеру жүргізу.
Қойылған міндеттерді шешу үшін келесі әдістер қолданылды:
- зерттелетін мәселе бойынша әдебиеттерді зерттеу және талдау;
- жалпы білім беретін мектептің жоғары сыныптарындағы математика мұғалімдерімен әңгімелесу;
- оқушыларды тестілеу;
- тәжірибелік жұмыс.
Зерттеудің әдіснамалық негізі: дамыта оқыту тұжырымдамасы (В. В. Давыдова, Д. Б. Эльконина) ; әрекеттік тәсілдің негізгі ережелері; «кеңістіктегі векторлар» тақырыбын зерттеу бойынша әдістемелік ұсынымдар (З. А. Скопец, В. А. Гусева, г. И. Саранцева) болды.
Зерттеудің жаңалығы: оқушылардың осы әдісті сәтті игеруі үшін қажетті дағдыларды қалыптастыру бойынша мақсатты алдын-ала жұмыс идеясына негізделген «оқушыларды есептерді векторлық әдіспен шешуге үйрету» тақырыбындағы әдістемелік ұсыныстардан тұрады.
Қорғауға шығарылатын мәселелер:
. Вектор - қазіргі математиканың іргелі ұғымдарының бірі. Қазіргі уақытта бұл ұғымды анықтауға бірнеше тәсіл бар.
. Векторлық әдіс-геометриялық есептерді шешудің және теоремаларды дәлелдеудің тиімді әдісі;
. Оқушылардың мазмұнды геометриялық есептерді шешудің векторлық әдісін сәтті игеруі үшін оларға оның құрамына кіретін дағдылар мен іс-әрекеттерді үйрету қажет;
. Векторлық әдістің мәні мынада: мәселенің шарты мен талабы векторлық формада жазылады, ал оның шешімі векторлық алгебраның заңдары негізінде шарттан талапқа ауысудан тұрады.
Дипломдық жұмыстың құрылымы оның логикасымен және зерттеу мәселелерін шешумен анықталады. Жұмыс кіріспеден, екі тараудан, қорытындыдан, әдебиеттер тізімінен, қосымшадан тұрады.
1 тарау. Мектеп геометрия курсында векторлық әдісті зерттеудің теориялық және әдістемелік ерекшеліктері
Бұл бөлімде векторлық әдісті оқытуға байланысты теориялық материалдар қарастырылады. Кез-келген тақырыпты зерттегенде, алдымен оның тарихын білу маңызды. Сондықтан 1 бөлімде векторлық әдістің пайда болу тарихына жүгінеміз. Одан кейін вектор түсінігін математикада және мектеп математикасында қарастырамыз. Оқушыларды есептерді шешуде векторлық әдісті қолдану зерттеуіне арналған әдістемелік тұжырымдаманы анықтау үшін, оқушыларды есептерді шешуге үйрету мәселесі бойынша психологиялық-педагогикалық әдебиеттерді және векторлық әдісті оқытуға арналған оқу-әдістемелік әдебиеттерді талдаймыз.
- Аналитикалық әдістің пайда болу және даму тарихы
Векторлар және векторлық әдіспен есептеу математиктерде 19 ғасырда физика мен механикада қажеттіліктен пайда болған. Алайда бағытталған кесіндімен есептеу оданда ертеректе қолданылған. Ежелгі Грецияда пифагорлар иррационалды сандарды ашқан соң ( , кез-келген санды бөлшекпен жазу мүмкін емес деген шешімге келді. Сондықтан сол кездің математиктері арифметика мен алгебраның есептерін шешуде геометриялық жолға келтірді. Осылайша, Евдокс Книдскийдің (408-355жж б. з. д) «Геометриялық алгебра» түсінігіне жол ашты.
Евклидтің «Бастамалар» кітабында қосу мен азайту кесінділерді қосу мен азайтуға, көбейту - ұзындығына сәйкес келетін көбейткіштерді тікбұрышты төртбұрыштарды кесінді арқылы салу, ал бөлу - геометриялық фигуралады "қолдану" операциясына дейін азайтылды.
16-17 ғасырларда геометриялық алгебра зерттеу мүмкіндігі шектелгендіктен дамуы тоқтап қалды.
Алайда, геометриялық есептеулер математиканың дамуына үлкен үлес қосты, оның ішінде векторлар теориясының пайда болуына ықпал етті.
Аристотельдің «Механикалық проблемалар» трактатында «механикалық қозғалыстарды қосу» деген термин бар, яғни жылдамдықтарын қосу, ол параллелограм ережесі арқылы жасалған. Оны Архимед «Спираль туралы» еңбегінде кейін Птолемей қолданған. Ортағасырлық Шығыс астрономдары Птолемей теориясын дамытып, «қозғалыстарды қосу» пайдаланған.
1587 жылы фламанд ғалымы С. Стевин (1548-1620) голланд тілінде «Статика бастамасы» трактаты жарыққа шыққан болатын. Онда автор күштердің қосылуы 90 бұрышпен қарастырғанда, «күштердің параллелограмын» қолдану керектігін көрсетіп, күштерді белгілеу кезінде стрелкамен салған. Стевин алғаш рет бір-біріне перпендикуляр екі векторды қосуды көрсетті. Одан кейін Стевин «Статика негіздері» мен Валлистің (1616-1703) «Механика» еңбектерінде параллелограм және параллелепипед ережелерін жасап бағытталған кесінділерді қосу үшін күш, жылдамдық пен үдеуді қолданды.
16 ғасырдың соңы мен 17 ғасырдың басында физик ғалымдар оның ішінде Леонардо да Винчи, Галилео Галилей, бағытталған кесіндіні күштерді түсіндіру кезінде қолданған. Кеплер планеталар қозғаласының заңдылығын ашқанда бағытталған кесіндінің басын Күннен бастап, соңын қозғалыстағы нүктемен қарастырған.
Бірақ бұл кезеңдерде нақты векторлық шамалар түсінігі қалыптаспаған, бағытталған кесіндімен алгебралық амалдар идеясы біртіндеп туындай бастаған.
Векторлық есептеулер 3 жолмен дамыды: геометриялық (кесінділерді есептеу), физикалық (векторлық шамаларды зерттеу), алгебралық (амалдарды кеңейту арқылы қазіргі алгебраны дамуы) .
Бағытталған кесіндімен есептеулер алғаш рет норвег ғалымы Каспар Вессельдің «Бағытты аналитикалық ұсыну тәжірибесін жазық және сфералық көрбұрыштарға қолдану» мемуарында 1799 жылы Дат Академиялық ғылымы еңбектерінде жарияланған. Вессель бұл еңбекті пратикалық есептеулерден кейін геодезисттердің жұмысын жеңілдету үшін жазған.
Вессель комплекс сандарды бағытталған кесінді ретінде көрсетті. Ол көбейту мен бөлу амалын бағытталған кесіндімен комплекс сандарға қолданды.
z 1 мен z 2 кесінділерді көбейткенде, бұл жерде z 1 =r 1 (cosα+isinα), z 2 =r 2 (cosβ+isinβ), онда z 1 *z 2 =r 1 *r 2 (cos(α+β) +isin(α+β) ) . Бұл ретте z 1 β бұрышына бұрылып, r 1 ұзындығы r 2 санына көбейтілген.
Векторлық алгебраны жазықтықта (немесе екі өлшемді кеңістікте) Вессельдің құрастыруы қазіргі кітап бойынша ұқсас болып келеді. Мысал ретінде оның векторларды қосу ережесін келтірсек: «Екі немесе оданда көп векторларды қосу үшін мына ережелерге сүйену керек: оларды біріншісінің соңы мен екіншісінің басын кездестіреміз, ал екіншінің соңы үшінші вектордың басына сәйкес келуі қажет т. с. с., содан кейін оларды біріншісі кесіндінің басталатын нүктесімен соңғы кесіндінің соңын кесіндімен жалғасақ осы екі кесіндінің қосындысына тең болады». Сонымен қатар, ол кеңейтілген қосу тұжырымдамасына ерекше жағдай және осы әрекеттің ескі мағынасы ретінде енгізілгенін атап өтті, яғни «егер қосылатын кесінділер бірдей бағытталған болса, онда қосындының бұл анықтамасы әдеттегі қосуға толық сәйкес келеді».
Вессель сонымен қатар кеңістіктегі (үш өлшемді векторлық кеңістік) бағытталған кесінділерді есептейді, және «Сфераның айналу алгебрасын» дамыта отырып, оны сфералық үшбұрыштар мен көпбұрыштарды шешуге қолданады. Вессельдің «Тәжірибесі» векторлық есептеулері қолданбалы геометрияның дамуына әкелгенін көрсетеді.
Мұны ұлы ғалымдардың табиғат құбылыстарын зерттеудегі математиканың рөлі туралы философиялық көзқарастары да айтады. Р. Декарттың координаттар жүйесі оның геометрия мен алгебраны біріктіретін біртұтас математика тұжырымдамасына негізделген. Декарттың жаратылыстанудың матемизациясы туралы ойларын дамыта отырып, Лейбниц былай деп жазды: «Алгебра позицияны тікелей білдіретін басқа, таза геометриялық талдау қажет». Лейбниц бағытталған кесінділерді, олардың ұзындығын, олардың арасындағы бұрыштарды зерттейтін геометриялық есептеулердің құрылысы туралы айтты. Бұл ойлар көптеген геометриялық жұмыстардың бастауы болды.
Векторлық есептеу тарихында Карноның «Геометрия орналасу» (1803) кітабы көрнекті орын алады. Онда автор геометриялық саны ұғымын енгізеді, ол негізінен бағытталған кесіндіні білдіреді және бағытты фигураларға, атап айтқанда кесінділерге қатысты іс-әрекеттермен айналысады. Оның алдында оң және теріс кесінділер тек бір түзу сызықта қарастырылды, сонымен қатар кез-келген бағыты бар кесінділерді енгізді және іс жүзінде векторлық есептеуге жол ашты. Карно енгізген кейбір терминдер мен символдар, атап айтқанда, вектордың жоғарғы жағындағы белгіні қолдана отырып белгіленуі (
 ,
,
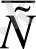 ) бүгінгі күнге дейін сақталған.
) бүгінгі күнге дейін сақталған.
1835 жылы Дж. Белаватис «Эквиполенттілік теориясында» ұзындығы бірдей және сәйкес бағыттары бар эквиполентті бағытталған кесінділерді атай отырып, еркін векторларды енгізді.
Аналитикалық және проективтік геометрия бойынша «Барицентрлік есептеу» (1827) шығармасында неміс математигі А. Мебиус белгілі бір дәрежеде Карноның жұмысын жалғастырып, оның идеяларын жүйелендірді. Автор алғаш рет АВ геометриялық санын нүктелердің айырмашылығы ретінде ұсынды: В - А.
Швейцариялық математик Жан Арган (1768-1822) 1806 жылы «Геометриялық салулардағы комплекс сандардың мөлшерін бейнелеу әдісі туралы тәжірибесін» жазды. Арган «бағытталған сызықтар» деп атайтын бағытталған кесінділердің есептеулерін құру мәселесін қояды және дұрыс шешеді. Шамамен сол уақытта бірқатар басқа жұмыстар пайда болды (М. Бюэ, Дж. Уоррен т. б. ), олар алгебралық ұғымдарды "сандар" мен "шамалар" теріс және комплекс сандарды және бағытталған кесінділерді қамтитындай етіп жалпылау әрекеттері жасалады.
Математикада бұл теория О. Кошидің «Алгебралық анализ курсынан» (1821) және Гаусстың «Биквадраттық шешімдер теориясынан» (1832) кейін түпкілікті расталды.
Векторлық есептеудің одан әрі дамуы гиперкомплексті сандарды зерттеумен байланысты, оның көмегімен кеңістіктегі бағытталған кесінділердің бұрылыстарын зерттеуге болады.
Ағылшын символдық алгебра мектебінің өкілдері Дж. Пикок (1791-1858), Д. Грегори (1813-1844), А. Де Морган (1806-1874), Дж. Гревс (1806-1870) триплеттерді, яғни өрнектерді зерттей отырып, бірқатар қызықты нәтижелерге қол жеткізді:
t=a+bi+cj,
мұндағы i 2 =-1, j 2 =-1, a, b, c - нақты сандар.
Алайда, олар триплеттермен операцияларды осылай орната алмады, сондықтан көбейту кезінде нөлге бөлінуден басқа бөлу операциясы мүмкін болады. У. Гамильтон бірнеше жыл бойы триплет операцияларын зерттеді. Үлкен есептеулер жүргізгеннен кейін, ол көптеген триплеттерде бөлу жүйесін құру мүмкін емес екеніне көз жеткізіп, кватерниондарды, яғни түрлердің өрнектерін зерттеуге көшті
w=a+bi+cj+dk,
мұндағы i 2 =j 2 =k 2 =-1, ij=-ji=k, jk=-kj=I, ki=-ik=j, a, b, c, d - нақты сандар.
Гамильтон өзінің «Кватерниондар туралы дәрістер» атты еңбегінде комплекс сандар алгебрасын қатаң баяндап, қазіргі векторлық есептеулерді дамытудың алгебралық көздерінің бірі болып табылатын ілім жасады. Жұмыста автор алдымен «вектор» терминдерін енгізеді (лат. vector - «тасымалдаушы немесе жетекші, тарту, беру»), » «скаляр», скалярлық және векторлық көбейтінділер, сонымен қатар үш өлшемді кеңістіктегі векторлармен операцияларды анықтайды. Ол былай деп жазды: «А нүктесінен В нүктесіне дейінгі қадамды қозғалмалы нүктені бастапқы күйден соңғы күйге ауыстыру немесе тасымалдау жұмысы ретінде қарастыруға болады».
Кватернион теориясын математик және физик П. Тэт (1831-1901) дамытып жетілдірді, ол кватернион теорияларын және оның 70 жұмысын физикаға қолдануға арнады. 1867 жылы «Кватерниондар теориясы бойынша қарапайым трактаттаны» Тэт алғаш рет аналитикалық геометрияның векторлық түсініктеме берді. "Түзу және жазықтық геометриясы" тарауында Тэт қазір оқулықтарға кіретін есептерді ұсынды: берілген екі нүктеден өтетін түзудің теңдеуін табыңыз; берілген нүктеден жазықтыққа түсірілген перпендикулярдың ұзындығын табыңыз; осы төрт нүктенің бір жазықтықта орналасқандығының жағдайын табыңыз және т. б.
Грассман «Ұзындық туралы ілім" (1844) еңбегінде алғаш рет n - өлшемді евклидтік кеңістігі туралы баяндайды, ол ерекше жағдай ретінде жазықтықта және үш өлшемді кеңістіктегі векторлар теориясын қамтиды. Автор таяқшалар деп атаған векторларды латын алфавитінің қалың әріптерімен белгіледі. Векторлардың скаляр көбейтіндісі, ол ішкі көбейтінді деп аталады, ол a b;
векторлық көбейтінді, сыртқы көбейтінді, ол [a, b] .
19 ғасырдың екінші жартысында векторлық есептеу идеялары негізінен физика саласында дамыды. Сент-Венан (1797-1886) Уоллис пен Стевиннің еңбектеріне сүйене отырып, «Геометриялық қосындылар мен айырмашылықтар және оларды механиканы ұсынуды жеңілдету үшін қолдану туралы» (1845) еңбегінде бағытталған кесінділерді қосу және азайту теориясын жасады. Джемс Кларк Максвелл (1831-1879), электромагниттік өріс теориясын жасаушылардың бірі, өзінің «Электр және магнетизм туралы ілімінде» векторлық есептеуді қолданды. Максвелл Тэтке: «Вектор идеясының мәні белгісіз», - деп жазды. Кватернион теориясының ол керегін алып, векторлық есептеу үшін қажет нәрсені таңдады және сол арқылы қазіргі физика кеңінен қолданатын ыңғайлы құрал жасады.
Американдық физик, химиялық термодинамика мен статикалық механиканың негізін қалаушылардың бірі - Дж. Гиббс (1839-1903), Грассман және ағылшын физигі О. Хевисайд (1850-1925) өзінің «Электромагниттік теориясында» векторларды қолданды.
19 ғасырдың соңғы ширегінде тарихи дамудың векторлық есептеулер үш жолында болды (геометриялық, алгебралық және физикалық) . Векторлық есептеу математиканың тәуелсіз саласына айналады.
Қазіргі математикада векторлармен әрекеттер туралы ілімді сипаттайтын бөлім векторлық алгебра деп аталады, өйткені бұл әрекеттер алгебралық әрекеттермен көптеген қасиеттерге ие. Сонымен қатар, Гамильтон айнымалы векторларды - векторлық функцияларды зерттейтін векторлық анализ жасады және векторлық аргумент (градиент) арқылы скаляр функцияның туындысын және векторлық аргумент функциясының туындыларының кейбір түрлерін-дивергенция мен роторларды анықтады.
Векторлық анализ тарихы математиканың жекелеген салаларының - алгебраның, геометрияның, математикалық талдаудың, комплексті айнымалы функциялар теориясының ажырамас байланысын көрсетеді. 16 ғасырда құрылған алгебралық теңдеулерді шешу үшін 19 ғасырдағы күрделі сандар гиперкомплексті сандар теориясын ашуға үлгі болды, бұл көп ұзамай ғалымдарды кватернион теориясына және векторлық есептеуге әкелді. Электр және магнетизмді зерттеуге арналған математикалық аппарат ретінде құрылған векторлық талдау физикалық теориялардың дамуына ғылыми негіз болды, нәтижесінде адамзат қазір қолданып жүрген өркениеттің артықшылықтарын құруға әкелді.
1. 2 Математика мен мектеп математика курсында Вектор ұғымын анықтаудың әртүрлі тәсілдері
Вектор - қазіргі математиканың іргелі ұғымдарының бірі. Бұл тұжырымдаманың эволюциясы оны математиканың, механиканың әртүрлі салаларында, сондай-ақ техникада кеңінен қолдану арқылы жүзеге асырылды.
7-сыныптағы физика сабақтарында векторлық шамалардың қатысуымен жүзеге асырылады. Бұл орта мектептің математика курсына вектор ұғымын қалай енгізу керектігі, оны теорияны ұсынуда және есептерді шешуде қалай тиімді қолдану керектігі, векторлардағы негізгі әрекеттерді қалай қарастыру керектігі туралы ойлануға мәжбүр ететіні түсінікті.
Бұл ұғымды түсіндіру бірнеше түрлері бар.
Л. Я. Куликовтың алгебра оқулығында [17] «F өрісінің үстіндегі n өлшемді вектор (мұндағы F - скаляр өрісі) F өрісінің n элементтерінің кез-келген жиынтығы деп аталады».
Бұл тәсілмен вектор әдетте жол немесе баған түрінде жазылады. Мысалы, (α 1 , α 2 , . . . , α n ), мұндағы α i -скалярлар.
Тең векторлардың анықтамасы енгізіледі.
Анықтама 1. Егер α
i
=β
i
,
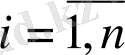 болса, (α
1
, α
2, …,
α
n
) және (β
1
, β
2, …,
β
n
) векторлары тең векторлар деп аталады.
болса, (α
1
, α
2, …,
α
n
) және (β
1
, β
2, …,
β
n
) векторлары тең векторлар деп аталады.
Сондай-ақ, n-өлшемді векторлар жиынында векторларды қосу, векторларды скалярға көбейту амалдары анықталған.
Анықтама 2. (α 1 , α 2, …, α n ) және (β 1 , β 2, …, β n ) векторларының қосындысы (α 1 +β 1 , α 2 +β 2, …, α n +β n ) векторы болады.
Анықтама 3. λ мен (α 1 , α 2, …, α n ) векторының скаляр көбейтіндісінен (λα 1 , λα 2, …, λα n ) векторы шығады.
Анықтама 4. (0, 0, …, 0) векторы - нөлдік вектор деп аталады. Нөлдік вектор қосуда нейтральді болады.
Анықтама 5. (-1) (α 1 , α 2, …, α n ) векторы а=(α 1 , α 2, …, α n ) векторына қарама-қарсы болады, а - деп белгіленеді.
Осыдан а+(-а) =0 екендігі көрінеді.
Сызықтық алгебра теориясында басқа абстрактілі тәсіл бар. Мысалы, [4] оқу құралында вектор V векторлық кеңістігінің элементі ретінде анықталады, ол бірқатар қасиеттерге ие:
1) (
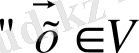 ) 1Ч
) 1Ч
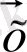 =
=
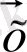 ;
;
2) (
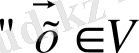 ) 0Ч
) 0Ч
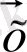 =
=
 ;
;
3) (
 ) αЧ
) αЧ
 =
=
 ;
;
4) (
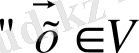 ) (-1) Ч
) (-1) Ч
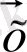 = -
= -
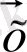 .
.
Бұл жағдайда вектордың анықтамасы қасиеттері арқылы енгізіледі.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz