Вектордың векторлық көбейтіндісі

Жұмыс түрі: Диссертация
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М. Әуезов атындағы Оңтүстік Қазақстан Университеті

ӘОЖ-514(023) қолжазба құқығында

Айтбаев Нуралы Жанарсович
Орта мектеп оқушыларына стереометриялық есептерді шығаруда векторлық әдіске үйрету әдістемесі

7M01510 - Математика білім беру бағдарламасы бойынша
педагогика ғылымдарының магистрі дәрежесін алу үшін
дайындалған диссертация

Ғылыми жетекшісі: т.ғ.к., доцент Кошанова М. Д

Шымкент 2022
Мазмұны

Кіріспе
3
1
Вектор ұғымының теориялық сипатталуы
6

0.1 Вектор ұғымы және оның шығу тарихы
6

1.2 Векторлар туралы жалпы түсінік
9
2
Стереометрияны оқытудың әдістемесі және стереометрия есептерін шешуде векторлық алгебра элементтерін пайдалану
16

2.1 Көпжақтар тақырыбын оқыту әдістемесі
16

2.2 Көпжақтар тақырыбына берілген есептерді векторлық алгебра элементтерін пайдаланып шығару
24

2.3Айналу денелері тақырыбын оқыту әдістемесі
46

2.4 Айналу денелері тақырыбына берілген есептерді векторлық алгебра элементтерін пайдаланып шығару
52

Қорытынды
58

Пайдаланылған әдебиеттер
59

Кіріспе

Қазіргі қоғамда қалыптасып келе жатқан ғылым және оқытушылық ақпараттардың даму қарқынына сәйкес мектеп математика курсының бағдарламасына көптеген талаптар енгізілуде.
Қоғамдағы қазіргі кездегі қайта құруларэкономиканы дамытудағы жаңа стратегиялық бағдарлар , қоғамның ашықтығы ,оның жедел ақпараттануы мен қарқынды дамуыбілім беруге қойылатын талаптарды түбегейлі өзгертті. Әлемнің жетекші елдерінің көпщілігінің білім берудің мақсатын, мазмұны мен технологияларын оның нәтижесіне қарай бағалайтын болды.
Жас ұрпақты жан - жақты жетілген, ақыл - парасаты,өресі биік өз Отанын сүйетін азамат етіп тәрбиелеудеғі басты тұлға ол - ұстаз. Қазіргі таңда жемісті еңбегімізбен шығармашылық ізденісіміз арқылы ғана реалды жаңару жолына шыға аламыз. Елімізге қажет болып отырған мамандарды бүгінгі күні мектеп партасында отырған математика, физика пәндерінен бейімділік танытқан оқушылардан тәрбиелеп, өсіріп шығаруға болатыны түсінікті. Бұл тұрғыда математика бағытында білім беріп жатқан мектептердің маңызы ерекше. Өйткені, осындай мектептердің түлектерінің басым көпшілігіөз білімдерін жоғарғы оқу орнында математика, техника салаларында жалғастырыатыны белгілі. Еліміздің жоғары оқу орындарымыздың физика- математика және техника салары бойынша мамандар дайындайтын факультеттерінің талапта да талантты студенттерінің бірқатары математиканы тереңдетіп оқытатын аталмыш мектептердің түлектері. Сондықтан жоғарыда айтылған математика мен физиканы тереңдетіп оқытатын мектептерге тиісті көңіл бөлу - уақыт талабы.
Математика ғылымын табысты дамыту үшін оқушылардың математикалық қабілеттерін қалыптастырып, олардың бойындағы дарындылықты жетілдіру қажет. Оқыту процесіндегі басты мақсат- оқушыларға дайын білімді беру ғана емес, сондай-ақ оларға дербес ойлауды үйрету. Осы мақсатқа орай оқушылырадың ой қызметтеріне азық бола алатын білім беру міндеті туып отыр. Оқушыларға кеңістіктегі вектор және координаталық әдіс тақырыбын ұғындыру- математика пәні мұғалімдері үшін қиын, күрделі меңгерілетін тақырып болып табылады. Себебі, аталған тақырыпқа байланысты әдістемелік құралдар аз жетілдірілген.
Математикада және оның қолданылуында кеңістіктегі вектор және координаттар әдіс ұғымы маңызды роль атқарады. Көп жағдайда координаттар жүйесін және векторларды қолдануға енгізілуі геометриялық есептерді шешуді жеңілдетті. Сонымен қатар мектеп курсындағы векторлық алгебра және аналитикалық геометрия элементтерін оқыту өте маңызды, өйткені, олардың жоғары математиканы оқуда білімдері өте қажет. Геометриялық теоремаларын дәлелдеу мен есептерін шешудегі барынша тиімді әдістердің бірі векторлық әдіс болып табылады. Есептерді жалпы түрде шешуде де векторлардың мәні зор.
Кеңістіктегі векторлық әдісті пайдаланып есептерді шешу кезінде берілген өрнектегі барлық белгілі, белгісіз шамаларды вектор тіліне ауыстыру қажет. Осылай жазу қиын болмаған жағдайда геометриялық есептерді кеңістіктегі вектор және координаталық әдісті пайдаланып шешуге болады.
Мектептің геометрия курсында кеңістіктегі векторды оқу арқылы, векторлардың көмегімен көптеген геометриялық есептер шешіледі. Есептерді шешудің белгілі тиімді әдістері қатарына енді векторлық әдістер де енеді.
Диссертациялық жұмыстың өзектілігі:геометриялық теоремаларды кеңістіктегі векторлық әдісті пайдалана отырып дәлелдеуді жүзеге асыру.
Кеңістіктегі векторлық әдісті пайдалана отырып дәлелденген теоремаларды есеп шығаруда пайдалануды іске асыру.Геометрияның стерометрия бөлімінің есептерін векторлық алгебраның элементтерін пайдаланып шешу жолдарын көрсету болып табылады.
Диссертациялық жұмыстың мақсаты: геометриялық есептерді кеңістіктегі векторлық әдісті пайдаланып шешудің алгоритмін құру.
Жұмыстың зерттеу нысаны:жалпы орта білім беретін мектептер
Диссертациялық жұмыстың : теориялық және әдістемелік негіздері
зертелетін тақырып бойынша математикалық ғылыми-әдістемелік әдебиеттер мен жұмыстарға талдау жүргізу;
орта мектептегі геометрияны оқу бағдарламасына талдау жасау;
математика мұғалімдерінің алдыңғы қатарлы тәжірибесін оқу және жалпылау.
Диссертациялық жұмыстың міндеттері:
мектеп математика курсындағы кеңістіктегі вектор тақырыбын терең ұғындырудың қажеттілігін ашып көрсету;
есептерді кеңістіктегі векторды пайдаланып шығаруда оның шешімін жылдам табуын, әрі тиімді шығару жолын ашып көрсету;
геометрияның стерометрия бөлімдерінің есептерін кеңістіктегі векторлық әдісті пайдаланып шешудің алгоритмін құру.
Диссертациялық жұмыстың ғылыми жаңалығы:
геометрияның стерометрия бөлімінің есептерін кеңістіктегі векторлық әдісті шешудің алгоритмін құру арқылы шешу;
стерометриялық есептерді шешуде кеңістіктегі векторлық әдісті қолданудың алгоритмін құру.
Жұмыстың практикалық құндылығы:
геометриялық теоремаларды кеңістіктегі векторлық әдісті пайдалана отырып дәлелдеуді жүзеге асыру;
кеңістіктегі векторлық әдісті пайдалана отырып дәлелденген теоремаларды есеп шығаруда пайдалануды іске асыру;
геометрияның стерометрия бөлімінің есептерін векторлық алгебраның элементтерін пайдаланып шешу жолдарын көрсету болып табылады.
Ғылыми мәселенің қазіргі кездегі шешу жағдайын бағалау: Өздеріңізге белгілі орта мектепте күні бүгінге дейін орыс тілінде шығарылған оқулықтар мен олардың түп нұсқасынан қазақ тіліндегі аудармалары қолданылып келеді. Мысалы: 7-11 сыныптарда геометриядан А.В.Погорелов (Алматы - Рауан баспасынан 1991ж) оқулығымен оқытылып келеді. Қазіргі кезде бұл оқулықпен геометрияны оқытуға қажетті дидактикалық материалдар азайып кетті, олар ауылдық жерде жоқтың қасы. Сондықтан мен дипломдық жұмысымды Стереометрия есептерін шығаруда векторлық алгебра элементтерін пайдаланып шығару тақырыбы бойынша қарастырдым.

1 Вектор ұғымының теориялық сипатталуы.

10.1 Вектор ұғымы және оның шығу тарихы
Қазіргі заман математикасының негізгі ұғымдарының бірі - векторлық кеңістік ұғымы. Бұл ұғым математиканың сызықтық алгебра, сызықтық прогрммалау,функционалдық анализ және физиканың кейбір салаларында қолданылады. Векторлар теориялық физикада,механикада, гидродинамикада, аэродинамикада, потенциалдар теориясында,қолданбалы математикада, химияда, экономикада, табысты қолданылып отыр.
Векторлық алгебра қазіргі заман математикасында қолданумен шектелмей жоғары оқу орындарында оқытылатын техникалық,математикалық пәндердің оқулықтарында лайықты орын алды. Векторлық алгебраның атқаратын рөлінің маңыздылығы соншалық аталмыш курстар векторлардың өздеріне қажетті тарауларын толығымен қамтиды. Дифференциялдық геометрия, аналитикалық, геометрия, математикалық физика, теориялық векторлар негізінде баяндалады.
Қазіргі кезде экономикалық есептердің көпшілігі векторлық алгебра көмегімен шешіледі. Компьютерді пайдаланып, дененің кескінін жасау үшін векторлық графика пайдаланылады.Сызықтық пограммалауда вектордың көмегімен көптеген практикалық мәселелер шешіледі.
Векторлық есептеулер математиканың жас салаларының бірі екендігіне қарамастан өзінің маңыздылығы арқасында, қолдану ауқымының кеңдігі арқасында кейінгі елу - алпыс жыл шамасында көптеген елдерде мектеп математикасына еніп, оның құрамдас бөлігі болып орнығып алды.
Векторлық алгебра мектептерімізде оқытыла бастағына ширек ғасырдан артық уақыт болды. Бірақ мұғалімдерге қажетті тарихи - әдістемелік материалдар әзірге дайындалмаған. Абстрактылығы жоғары векторларды оқушыларға саналы түрде меңгерту үшін, олардың векторларды оқып білуге деген ынтасын арттыру үшін тарихи мағлұматтар бере отырудың маңызды екендігі сөзсіз. Математика пәнінің мұғалімдері векторлық есептеулердің жасалу тарихын, векторлардың қолдануларын, ғылым мен техника салаларындағы маңыздылығын білгендері маңызды. Жоғарыда айтылғандарды ескере келе мұғалімдердің пайдалануына арнайы дайындалған, векторлық есептеулердің жасалу тарихын қысқаша мазмұнын төменде беріп отырмыз.
Техникалық ғылымдардың қауырт дамуына байланысты он сегізінші ғасырдың өзінде- ақ есептеу аппаратын жетілдірудің қажет екендігі байқалды. Бұрыннан қолданынып келген есептеу түрлері ендігі жерде қажеттілікті қанағаттандыра алмайтын болып шықты. Теориялық физиканың жедел де аса күшті қарқынмен дамуына байланысты он тоғызыншы ғасырдың басында математиканы жетілдіруге деген талап күшейе түсті. Есептеудің талапқа сай жаңа түрін ісдестіру қажет болды. Нәтижесінде он тоғызыншы ғасырдың екінші жартысында векторлық есептеулер дүниеге келді де, үлкен қарқынмен тез дамыды және математиканың бір бөлігі болып қалыптасты.
Векторлық есептеулерді жасауға көптеген елдердің ғалым-математиктері, физик-механиктері, инженер-техниктері қыруар үлес қосты. Векторлық есептеулердің жасы жас болғанымен бастау көзі сонау ерте заманда өмір сүрген данышпан Аристотельдің Механикалық проблемаларатты еңбегінде табылды. Аристотель осы еңбегінде бір нүктеге түсірілген және де бұрыш жасай бағытталған екі күштің әсерінен дененің жүрген жолын табуды екінші мәселе етіп қояды. Оның жиырма төртінші мәселесінің мазмұны мынадай: Ромбтың қабырғасының бойымен бір-бірімен қарама-қарсы бағытта екі нүкте бірдей жылдамдықпен қозғалып келеді. Ромбтың қабырғасы дәл сондай жылдамдықпен қарсы жатқан қабырғаға қарай қозғалады. Әр нүктенің жүрен жолы қандай? Жауап: әр нүкте ромб диагоналі бойымен қозғалады.
Сұрақ: бірдей жылдамдықпен қозғалып келе жатқан нүктелер бірдей уақытта неге әртүрлі жол жүреді? Міне осыдан Аристотельдің қозғалыстарды (орын ауыстыруларды) қосуға параллелограм ережесін қолданғандығы векторлардың геометриялық қосындысын табудың қазіргі, біз қолданып жүрген түріне өте жақын келгендігі байқалады. Он жетінші ғасырда Аристотельдің қозғалыстар паралеллограмы қайтадан жанданды. Галилео Галилей(1564-1642) күш және оның денені қозғайтын құраушысының арасындағы метрикалық байланысты зерттеді. Оның еңбектеріне қарап, Галилейдің теңәсерлі күш, қорытқы жылдамдық ұғымдарына жақын, қапталдас келгенін көруге болады. Ағылшын математигі, әрі физигі атақты Исаак Ньютон (1643-1727) қозғалыстарды қосуға алғаш рет параллелограмм ережесін пайдаланды. Неміс математигі Готфрид Вильгельм Лейбниц (1646-1716) геометриялық есептеулер идеясын берді, алайда әрі қарай дамытпады. Механикадағы векторлық алгебраның негізін қалаушы Джон Валлис(1616-1703) механикаға геометриялық аппарат жасап беруде жаңа әрі асаірі қадам жасады. Ол екі, үш күштің тең әсерлі және қорытқы күшін табуға, қорытқы жылдамдықты табуға қолданылатын параллелограмм ережесін ғылымға алғаш енгізген Джон Валлис болды. Күштерді, жылдамдықтарды қосу, жіктеу, векторды санға көбейту амалдарын алғаш берген осы адам.
Он сегізінші ғасырда математика мен механикада аналитикалық әдістермен әуестену басым болды. Леонард Эйлер (1707-1783) мен Лагранждың арқасында механика математиканың жаңа бір саласы болатын жағдайға жеткізді. Тек қана он сегізінші ғасырдың ақырғы кезінде Монждың (1746-1816) геометрия мектебінде геометриялық есептерге қайта ұмтылыс байқалды. Әсіресе кинематикадағы қозғалыстарды қозғалыстарды зерттеуге геометриялық әдіс аса тиімді болып шықты. Л.Карно бұл бағытта аса табысты еңбек етті. Ол Қозғалыстың геометриялық теориясын жасау мәселесін көтерді, векторды қосудың көпбұрыш ережесін және қазір пайдаланып жүрген векторлық алгебраның символдық аппаратаын жасап шықты. Множ-Понселе мектебінің көрнекті өкілі Баре де Сен-Венан(1797-1886)серпімділік теориясындағы, гидродинамикадағы,термодинамикадағы ,жалпы механикадағы тамаша еңбектерімен белгілі физиктер мен механиктер ортасында аса танымал тұлға еді. Сен-Венан векторлық алгебра саласына өлшеусіз үлес қосты. Об геометрических суммах и разностяхи их применение для упрощения механики атты 1845-жылы жарияланған еңбегінде Сен-Венан скаляр көбейтінді, векторлық көбейтінді,вектор функцияны дифференциалдау, интегралдау ережелерін берді.
Осы еңбегі арқылы Сен-Венан механиканы вектор негізінде құрудың жалпы схемасын жасап шықты. Понселе мектебінің шәкірті Резаль(1820-1896) 1862 жылы жарияланған Чистая кинематикаеңбегінде Сен-Венан жасаған векторлық есептеуді жетілдіре түсті және векторлық есептеудің кинематикада қолданылуына көптеген мысалдар көрсетті
Векторлық алгебраның негізін салушылар Ирландия математигі әрі астраномы Уильям Гамильтон(1805-1865)және неміс математигі Герман Грассман (1809-1877) деп айтылып жүр. 1844-жылы Уильям Гамильтонның векторлық есептеулерге арналған алғашқы мақалалары және Герман Грассманның Учение о претяженностиатты көлемді еңбегі жарияланды. 1853-жылы Гамильтонның Лекция о кватернионах атты еңбегі жарық көрді. Бұлардың әрқайсысы векторлық есептеудің жаңа әрі әмбебап түрін жасады және векторлық есептеулерге қыруар еңбек сіңірді. Вектор ұғымын 1846 жылы ғылымға енгізген Гамильтон болды. Д.Валлис, Л.Карно, Сен-Венан, Резаль бұлар векторлық алгебра мен векторлық анализдің негізгі ұғымдарын ғылымға енгізді, механикаға қажетті геометриялық аппарат жасау жолында жемісті еңбек етті. Есептеудің жаңа түрі бойынша жинақталған бай, мазмұнды материалды ортақ бір идея бойынша біріктіріп, механикалық тұғырынан ажыратып, бұл аппаратты математикалық пән дәрежесіне көтеру керек болды. Осыны Санкт-Петербург университетінің профессоры Иосиф Иванович Сомов
(1815-1876) өзінің 1864 жылы жарық көрген Об ускарениях различных порядков деп аталатын еңбегінде абыроймен орындап шықты. Жоғарыда аттары аталған, векторлық есептеулерді жасауға еңбек еткендердің негізгі көпшілігі векторлық есептеулерге инженер көзімен қараса, И.И.Сомов математика көзімен қарады. Ол векторлық есептеулерді математикалық пән дәрежесіне көтерді. Сөйтіп, векторлық есептеулерге студенттер аудиториясына жол ашты: векторлық есептеулерді механика оқулығына енгізді, ең алғашқы болып, дифференциал геометрияны вектролық алгебраны пайдаланып жазып шықты. Ол векторлық есептеулердің бірқатар ұғымдары мен теоремаларын жасады. Векторлық алгебраны пайдаланғанда нәтиже координаталар жүйесіне тәуелсіз екндігін ол бірінші болып айтқан адам. Айналмалы қозғалысты сол сияқты қисықтың бұралуын зерттеу жұмыстарына векторлық көбейтіндіні қолданған да И.И. Сомов болды. 1918 жылы танымал математик Герман Вейль (1885-1955) векторлық аксиоматиканы берді. Вейль аксиоматикасы қазіргі заман геометриясында пайдалануға аса қолайлы болып отыр. Векторлық есептеулерді жасауға үлес қосқандардың ең көрнекті өкілдеріне тоқталып өттім. Ғылымның бұл саласын дамытуға, практикада қолдануға бұл ғалымдардан басқа да үлес қосқандар аз болған жоқ. Солардың қатарында: К.Бессель(1745-1818), К.Гаусс(1777-1855), Д.Гибб (1839-1903), Г.Белловитис(1803-1880), К.Максвелл(1813-1879), Л.Лоуренс (1901-1958), А.Мебиус(1790-1858) Арган(1768-1882) т.б атауға болады.
Векторлық есептеулерді және олардың тамаша қолдануларын дамытуға И.И.Сомовтан басқа да орыс және Кеңес ғалымдарының қосқан үлесі өте үлкен болды. Осы тұрғыда атақты математик - Санкт-Петербург акедемиясының академигі М.В.Острогадскийді(1801-1919) және П.А.Котельников, А.Л.Фридман, Н.Е.Кочин, Я.И.Френкель(1894-1952), П.А.Широков(1895-1944), Д.И.Зейлиегер(1864-1936) сияқты ғалымдарды атаған жөн.

10.2 Векторлар туралы жалпы түсінік.

Бағытталған кесінді (немесе реттелген қос нүкте) вектор деп аталады.

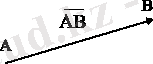
1-сурет
А нүктесі вектордың бастапқы нүктесі (басы), ал В-соңғы нүктесі (ұшы) деп аталады.Векторды былай белгілейді: .а = AB.
Математика мен физикада және механикада зерттелетін шамаларды екі топқа бөлуге болады.Бірінші топқа сан мәнімен толық анықталатын шамалар жатады.Мысалы, ұзындық, аудан, көлем, уақыт, бұрыш, температура, тығыздық, жұмыс, масса т.б. Біз, егер ауаның температурасы 120С десек, онда ауаның температурасы осы шамамен толық анықталады.Осындай сан мәнімен толық анықталатын шамаларды скаляр шамалар деп атайды.
Алайда сан мәнімен толық анықталмайтын шамалар да кездеседі.Мысалы, күш, жылдамдық, үдеу т.б. тек сандық мәнімен ғана емес, бағытымен де сипатталатындығы физикадан белгілі.Бұл шамаларды толық сипаттау үшін, олардың мәндерімен қатар бағыты да белгілі болуы керек.Мұндай шамаларды векторлық шамалар деп атайды.
Кез келген скаляр шаманы сан түзуінің кесіндісімен сипаттауға болады, ал векторлық шаманы бағытталған кесінділермен немесе бастапқы және ақырғы нүктесі белгіленген кесіндімен, яғни вектормен сипаттауға болады.
Сөйтіп, вектор дегеніміз-бағытталған және басы мен ұшы белгіленіп көрсетілген кесінді.Вектордың бағыты басынан ұшына қарай алынады.
Кесіндінің негізгі сипаттамасы-тек қана ұзындығы.
Ал вектордың сипаттамасы: 1) басы (бастапқы нүктесі; 2) бағыты; 3) ұзындығы (немесе модулы).Бұл сипаттамалардың әрқайсысы өзінше маңызды.Осы сипаттамалардың біреуі кем болса, вектор анықталмайды.Вектордың модулы әрқашан да оң таңбалы болады.
Вектор ұғымымен қатар математикада бағытталған түзу немесе осы ұғымы да маңызды роль атқарады.
Жәй мағынасына сәйкес вектор деп бағытталғн кесінді деп түсінуге болады, ал басқа жағдайларда әр-түрлі векторлар - белгілі бір эквиваленттік қатынасы бойынша әр-түрлі бағытталған кесінділер эквивалентті класстары болып табылады. Бұл эквиваленттік қатынасы әр-түрлі болуы мүмкін: ол векторлардың түрін анықтайды ("еркін", "тұрақты" т.б.). Басқаша айтқанда, эквивалентті класс ішінде кез келген екі вектор тең болып есептеледі, яғни кез келген вектор сол класты толықтай бейнелей алады.Еркін векторлар жиыны мен олардың кеңістікті параллель жылжыту жиыны арасындағы изоморфизмды ескерсе, егерде қосу операциясын жылжыту композицияларымен теңестірсе, онда кеңістікті параллель жылжыту жиынын тіпті векторды анықтау үшін де пайдалануғы болады.Кеңістікті шексіз аз трансформацияларын зерттеуде маңызды рөл атқарады.
Кейде, векторлар ретінде "барлық" тең бағытталған кесінділер жиыны орнына осы жиынның әлдебір өзгертілген түрін (фактор жиынын) айтады. Осылайша еркін (барлық ұзындықтары мен бағыттары бірдей векторларды бір (толықтай бірдей) деп қарастырады), сырғанақ (еркін мағынасы байынша тең векторларды егер бас нүктелері мен соңғы нүктелері бір түзудің бойында жатса) және тұрақты векторлар (іс жүзінде бағытталған кесінділердің бас нүктелері әр-түрлі болса - векторлар тең емес деген сөз).
Вектор үш түрге бөлінеді: 1) байламды вектор; 2) сырғымалы вектор; 3) еркін вектор.
Байламды вектор деп басы белгілі бір нүктеге бекітілген, одан басқа нүктеге көшіруге болмайтын векторды айтады.Мысалы, күш белгілі бір нұктеге байланысты болса, онда оны басқа жерге көшіруге болмайды.
Сырғымалы вектор деп бір түзудің бойымен жылжитын векторды айтады.Мысалы, қатты затқа әсер ететін күш немесе жылдамдық сырғымалы вектор болады.Мұндай векторды өзі орналасқан түзудің бойындағы кез келген нүктеге көшіруге болады, ал оны басқа түзудің бойындағы нүктеге көшіруге болмайды.
Еркін вектор деп сол вектор жатқан түзудің бойымен жылжытуға болатын және өзіне-өзі параллель көшіруге болатын векторды айтады, яғни вектордың бастапқы нүктесі кеңістіктегі кез келген нүктеге көшірілетін болса ондай вектор еркін вектор деп аталады.Механикада векторлардың осы үш түрі де кездеседі.
Біз тек қана еркін векторларды қарастырамыз.Математикада негізінен вектордың түсу нүктесі маңызды орын алмайтын есептер ғана қарастырылады.
Егер вектордың басы M, ал оның ұшы N болса онда оны МN символымен белгілейді.Кейде векторды белгілеу үшін кіші латын әріптерін қолданып, олардың үстіңгі жағына стрелка қоятын боламыз.
Анықтама: Вектордың бастапқы және соңғы нүктелері беттесіп кетсе, оны нолдік вектор деп атайды. Нолдік векторды былай белгілейді: 0 Нөл векторлардың бағыттары анықталмаған, модульдері нөлге тең.
Анықтама:Вектордың басы мен ұшының ара қашықтығы оның ұзындығы немесе модулі деп аталады. Былай белгіленеді: .анемесе AB.
Анықтама: Модульдері бірге тең векторлар бірлік немесе орт вектор деп аталады.
Бірлік вектор (орт) -- ұзындығы бірге тең вектор: . Басы мен ұшы беттесетін вектор нөлдік вектор деп аталады. Нөлдік вектордың модулі нөлге тең: бағыты анықталмаған. Бір түзудің бойында немесе параллель түзулердің бойында жататын векторлар коллинеар векторлар деп аталады. Коллинеар векторлар бағыттас немесе қарама-қарсы бағытталған бола алады.
Нөлдік вектор кез келген векторға коллинеар деп есептеледі. Нөлдік емес екі вектор қарама-қарсы бағытталған және ұзындықтары тең болса, онда оларды қарама-қарсы векторлар деп атайды.
Қарама-қарсы векторлардың қосындысы нөлдік векторға тең. Бір жазықтыққа немесе параллель жазықтықтарға тиісті векторлар компланар векторлар деп аталады.
Анықтама: Бір түзудің немесе параллель түзулердің бойында жатқан векторлар коллинеар деп аталады.
Анықтама: Өзара коллинеар, ұзындықтары тең және бағыттары бірдей векторлар тең векторлар деп аталады.
Анықтама: Параллель көшіруге болатын векторларды бос векторлар дейді, яғни бастапқы нүктесіне тәуелсіз, тек векторының ұзындығы мен бағытына ғана тәуелді вектор.

10.3 Векторларға амалдар қолдану
Ғылым мен техникада кездесетін кейбір шамалар тек сан мәнімен ғана сипатталады (абсолют шамасымен). Мысалы: масса, уақыт, темпиратура, және т.б. Бұл шамаларды скаляр шамалар дейді. Ал, кейбір шамалар сан мәнімен ғана емес, сонымен қатар бағытымен де сипатталады. Мысалы: күш, үдеу, жылдамдық, импульс және т.б. Бұл - векторлық шамалар. Бір қызығы жоғарыда айтылған барлық векторлық шамалар механикада кездеседі. Алайда механиканың дамуы кезінде векторлық анализ тіпті болмаған. Векторлық анализ тек Максвелдің электромагниттік теориясынан кейін ғана пайда болған. Себебі: электр және магнит өрістерінің табиғаты - векторлық.
Кез-келген вектордың ұзындығы (вектордың шамасына пропорционал) мен бағыты болады. Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын шамалар векторлық шамалар немесе векторлар деп аталады.Сонымен, орын ауыстыру векторлық шама болып табылады. Векторларды бағытталған кесінді түрінде кескіндейді және бір әріппен немесе вектордың басы мен ұшын көрсететін екі әріппен белгілеп, төбесіне нұскама (стрелка) қояды. Кез келген вектордың сандық мәні оның модулі деп аталады.Модуль -- скалярлық шама. Егер α және в векторларының модульдері мен бағыттары бірдей болса, онда олар тең болады . Ал векторлардың модульдері тең болып, бірақ бағыттары қарама-қарсы болса, онда а = - b болады.
Векторларды қосу.Мысалы, кез келген ажәне b векторлары берілсін. Осы векторларды қосып, а+ b-ға тең болатын с векторын табу керек. Ол үшін векторды өзіне-өзін параллель көшіргенде вектор өзгермейді дейтін ережені пайдаланамыз. Осы ереженің көмегімен векторларды қосудың бірнеше тәсілдерін көрсетуге болады. Мысалы, екі векторды бастарын түйістіре параллелограмның екі қабырғасы болатындай етіп өз-өзіне параллель көшіреміз де, параллелограмм саламыз. Сонда екі вектордың шыққан нүктесінен жургізілген бағыты көрсетілген диагональ қорытқы вектор болып табылады . Векторларды осылайша қосу параллелограмм ережесі бойынша қосу деп аталады.

2-сурет

Векторларды қосуда үшбұрыш ережесін де қолдануға болады. Ол үшін берілген векторларды бірінші вектордың ұшы екінші вектордың басымен түйісетіндей етіп, өз-өзіне параллель көшіреміз. Сонда бірінші вектордың басынан екінші вектордің ұшына қарай жүргізілген вектор сол екі вектордың қосындысын береді. Ал енді екеу емес, бірнеше векторды қосу керек болса. Онда векторларды, алдыңғы вектордың ұшына келесі вектордың басы жалғасатындай етіп, әркайсысын параллель көшіреміз. Сонда алынған көпбұрыштың басы мен ұшын тұйықтап тұрғанРвекторы қорытқы вектор болып есептеледі. Ол бірінші вектордың басынан соңғы вектордың ұшына қарай бағытталады және мынаған тең болады: Р=a+b+c +d.
Векторларды азайту. Векторларды косу ережесінен векторларды азайту ережесін шығарып алуға болады. Мысалы, а- b=с векторын табу керек болсын. Бұл теңдікті с = а + ( - b) түрінде жазуға болады, яғни векторлардың айырымын табу үшін а азайғыш векторға модулі азайткыш векторға тең, бірақ оған карама-карсы бағытталған - bвекторын қосу керек. Немесе екі векторды өздеріне параллель көшіріп, бастары бір нүктеден шығатындай етіп орналастырамыз. Содан соң олардың ұштарын азайтқыштан азайғышка қарай бағытталған вектормен қосамыз. Міне, осы с векторы қорытқы вектор болады.

3- сурет

Бір түзудің бойында жатқан немесе бір-біріне параллель векторлар бір жаққа қарай не қарама-қарсы бағытталуы мүмкін. Мұндай векторлар а және b векторлары сияқты қосылады, яғни бірінші вектордың ұшы екінші вектордың басымен қосылады. Қорытқы вектор модулі бойынша қосылатын векторлар модульдерінің арифметикалық қосындысына немесе арифметикалық айырымына тең. Қорытқы вектор қосылатын векторлармен бағыттас модулі үлкен вектор жаққа қарай бағытталады.
Векторларды скалярға көбейту (бөлу) Берілген a векторын кез келген к скалярға көбейту (бөлу) үшін осы вектордың модулін берілген санға көбейтеміз (бөлеміз): b = к :: а (b = а :к). Қорытқы bвектордың бағыты к көбейткішінің (бөлгішінің) таңбасымен анықталады. Егер к оң болса (к 0), онда b векторы а векторымен бағыттас, ал к теріс болса (к 0), b векторының бағыты a векторының бағытына қарама-қарсы болады.

4- сурет

a және b векторларының скаляр көбйтіндісі бұл векторлардың модульдерінің осы векторлардың арасындағы бұрыштың косинусының көбейтіндісіне тең. Яғни (a, b) =a · b cos∠(a, b), мұндағы ∠(a, b) дегеніміз a және b векторларыныңарасындағыбұрыш.
Скаляр көбейтіндінің қасиеттері:
1 (a, b) = (b, a)
2 (a, a) = a2
3 (a+b, c) = (a, c) + (b, c)
4 (a -b, c) = (a, c) -(b, c)
5 (k ·a, b) = (a, k ·b)=k ·(a, b)
Скаляр көбейтіндісінің геометрикалық интерпретациясы.
a және b векторларының (a , b ) скаляр көбйтіндісі бұл векторлардың модульдерінің осы векторлардың арасындағы бұрыштың косинусының көбейтіндісіне тең.Яғни (a, b) =a · b cos∠(a, b), мұндағы ∠(a, b) дегеніміз a және b векторларының арасындағы бұрыш.
Вектордың векторлық көбейтіндісі. Геометриялық мағынасы. Егер а және b векторлары басы ортақ болса , онда a*b векторлық көбейтіндінің модулі осы векторлардан құралған параллелограмның ауданына тең болады.Координаттық түрде берілген берілген векторлық көбейтінді.Егер , онда a*b мына формуламен өрнектеледі:

Аралас көбейтінді. Нөлдік емес үш вектораларының аралас көбейтіндісі деп, және векторларының векторлық көбейтіндісі мен векторының скалярлық көбейтіндісіне тең.Аралас көбейтіндінің қасиеттері:
1 яғни көбейтудің орындалу ретін өзгертуге болады, сондықтан аралас векторлардың көбейтіндісін түрінде жазуға болады.
2 Аралас көбейтіндіде көбейткіштердің орындарын ауыстырған кезде олардың таңбалары ауысады, мысалы
3 Егер берілген үш вектордың екі векторы өзара тең немесе коллинеарлы болса, онда аралас көбейтіндісі нөлге тең болады.
вектордың компланар болуының қажетті және жеткілікті шарты Векторларға қолданылатын сызықтық амалдар.

4 Анықтама bвекторын нақты λ санына көбейту деп мына шарттарды қанағаттандыратын b векторын айтады
5 ba*λ
b вектор a векторына коллинеар.
b және a векторының бағыттары бірдей, егерλ0 және қарама-қарсы бағытталған, егерλ0 . Егердеλ=0 болса, онда векторлардың бағыттары анықталмаған, яғни кез келген бағытты қабылдайды.
Векторларға сызықтық амалдар қолданудың негізгі қасиеттері.
1-қасиеті. Кез келген α және β сандары және а векторы үшін мына теңдік орындалады:α(βа)=αβа
2-қасиеті. Екі вектордың қосындысында ауыстырымдылық заңы орындалады, яғни кез келген екі вектор. А +b=b+а
3-қасиеті. Үш вектордың қосындысына терімділік заңы орындалады, яғни әруақытта а + (b + с)=(а +b) + с болады.
4-қасиеті. Векторлардың қосындысын санға көбейту үлестірімді, яғни кез келген b;а , векторлары мен α саны үшін мына теңдік орындалады:α (а +b)= αа + αb
5-қасиеті. Кез келген α,β сандары және кез келген а векторы үшін теңдігі орындалады. Екі бөлігіндегі векторлар өзара коллинеар.
Анықтама: Параллель көшіруге болатын векторларды бос векторлар дейді, яғни бастапқы нүктесіне тәуелсіз, тек векторының ұзындығы мен бағытына ғана тәуелді вектор.

2 Стереометрияны оқытудың әдістемесі және стереометрия есептерін шешуде векторлық алгебра элементтерін пайдалану
2.1 Көпжақтар тақырыбын оқыту әдістемесі
Геометриялық білімдерінің дүниетанымдық бағытын жетілдіре түсу үшін оқушыларға мазмұндау, шығу тегін түсіндіру, математикалық теориялардың дамуы мен құрылуы жайлы айту керек, яғни түсініктерді, тұжырымдарды, ережелер мен есепті шығару әдістерін және олардың арасындағы қатынастарды түсіндіру қажет. Жүргізілген тәжірибелердің математиканы дамытуда әсер ететін пайдасы мол екенін немесе керісінше математиканың тәжірибе жүзінде көптеген мәселелерді шешіп жүргендігін көрсетіп, жүйелі түрде оның жолдарымен таныстырып отыру маңызды..
Көпжақтар тақырыбына берілген есептерді векторлық алгебраның элементтерін пайдаланып шығару үшін ең алдымен көпжақтар тақырыбын тереңірек оқып үйренуіміз керек деп ойлаймын. Ол үшін көпжақтарды оқыту барысында оқушылардың кеңістік түсінігін дамыту бағытындағы жұмыс жалғастырылады және көпжақтар тақырыбын оқытудың әдістемесі қарастырылады.
Көпжақтар тақырыбы стереометрияның мектеп курсының, мүмкін, айналу денелерін оқытудан басқа барлық тақырыптардан гөрі әртүрлі көрнекі құралдарды қолданудың кең мүмкіндігін жасайды. Көрнекілік кез келген оқытудың міндетті сапасы болып табылады. Мақсатты іс-қимылдар арқылы біз оқушылардың санасында ұғымдардың қайсыбір жүйесін, олардың арасындағы байланыстарын қалыптастырамыз. Оқыту сәтті болуы үшін оқушы бұл жүйені қабылдай алуы және онымен жұмыс жасай алуы керек. Бірақ ол үшін, өз кезегінде, оқушыға қайсыбір материалдық модельді ұсыну қажет. Бұл үшін оқытудың көрнекі құралдарды қолданады. Мысалы, егер пирамида ұғымы оқытылатын болса, онда мұндай модель ретінде келесілер болуы мүмкін: 1) осы ұғымды сөзбен суреттеу (бейнелеу) (анықтау); 2) пирамиданың көлемдік моделі (каркастық немесе тұтас); 3) оның жазбасы; 4) пирамиданың немесе оның жазбасын тақтада, қағаз бетінде, экранда және т.с.с. бейнелеу. Барлық аталған нысандар пирамида ұғымын белгілі бір жағынан сипаттайтын материалдық модельдер болып табылады.
Көпжақтарды зерттеуде көлемдік модельдер негізгі көрнекі құралдар болып табылады. Әртүрлі материалдардан жасалған осындай модельдер әртүрлі дидактикалық мақсаттарға сәйкес келеді. Мысалы, картоннан жасалған модельдер көмегімен көпжақтың формасын көрсетуге болады. Сонымен қатар, мұндай модельдерде дененің жазбасын көрсету ыңғайлы. Бірақ картонның мөлдір еместігі кесірінен картоннан жасалған көпжақтарды денелердің қималары мен тіліктерін және бірінің ішіне бірі сызылған денелерді көрсету мүмкін болмайды. Әйнек модельдерді көпжақтың қимасы мен тілігін немесе оған іштей сызылған басқа геометриялық денелерді көрсету қажет болғанда қолдану ұсынылады. Ағаш модельдер беріктігімен ерекшеленеді. Сымнан жасалған каркастық модельдерде стереометрия сабақтарында кеңінен қолданылады. Олар көпжақтың түрлерін, элементтерін және жазықтыққа проекциясын (модельдің ақ қағаз бетіндегі көлеңкесін), көпжақтың жазықтықпен қимасын, геометриялық денелердің комбинацияларын көрсетуге мүмкіндік береді. Мұндай модель көпжақтың көлемдік моделі мен қағаз бетіндегі сызбасы арасындағы байланыс қызметін атқарады. Каркастық модельдердің сабақта қолдануға болатын серияларын атауға болады: дұрыс призмалар мен пирамидалардың (толық және қиық) модельдерінің жиынтығы, төбелері табан диагональдарының қиылысу нүктесіне проекцияланатын (модельдің негізгі контурдан бөлек, биіктігі, табанының диагональдары және бүйір жақтарының биіктіктері болуы тиіс) төртбұрышты пирамидалардың модельдерінің жиынтығы, көпжақтардың комбинацияларына қатысты модельдер жиынтығы.
Өндірісте шығарылатын модельдер мектеп оқушыларын математикаға оқыту барысында пайда болатын қажеттіліктерді қанағаттандыра алмайтын жағдайлар да болуы мүмкін. Сондықтан көбінесе мұғалімдер модельдерді оқушыларды қатыстыра отырып өздері дайындайды. Бұл тек мектепте қажетті модель, құрылғы немесе құрал болмаған жағдайларда ғана емес, сонымен қатар, мұғалім қолда бар модель, құрылғы немесе құрал оқытылып отырған материалды оқушының анық та нақты түсініп, қабылдауына жеткіліксіз болған жағдайларда да жасалады. Модельге жетілдірулерді енгізе отырып, ұстаз шәкірттерін модельдің жаңа нұсқасын жасауға тартады. Бұл әрекет өз кезегінде оқушылардың терең де тиянақты білім алуларына және олардың алған теориялық білімдерін іс жүзінде қолдануларына жағдай жасайды. Фабрикада жасалған модельдерді де, қолдан жасалған модельдерді де жаңа ұғымдарды енгізу барысында, теоремаларды дәлелдеу барысында және тәжірибелік және зертханалық жұмыстарды орындау барысында қолдануға болады.
Оқу құралдарының тағы бір ыңғайлы түрлерінің қатарына әртүрлі жазық немесе көлемдік фигуралар, графиктер, кестелер және т.с.с. бейнеленген резеңкі штемпельдерді (штампылар) жатқызуға болады. Өкінішке орай, қазір мұндай оқу құралдары мектептерде өте сирек кездеседі. Оқу құралдарының бұл түрін қолдану барысында қажетті бейнені, мысалы, текшенің немесе тікбұрышты параллелепипедтің бейнесін алу үшін, штемпельді штемпель жастығына тақап, содан соң қағаз бетіне басу жеткілікті болады. Текшенің немесе тікбұрышты параллелепипедтің бейнелерін салуға қатысты есептерді шешу кезінде оқушылар штемпельді қолдана отырып дәптер бетінде дұрыс сызбаны тез ала алады, ал бұл уақыт үнемдеуге мүмкіндік береді. Әрине, штемпельдерді қолдану оқушыларды фигураларды салу біліктіліктерін жоғалтуға алып келмеуі тиіс. Сондықтан ұстаз алдымен оқушыларды жазықтықта фигураларды бейнелей алуға үйретуі тиіс, содан кейін ғана штемпельдерді сабақ барысында қолдануға үйретуі керек. Штемпельдерді мұғалім көпнұсқалы бақылау жұмыстарын дайындау кезінде қолдана алады. Мысалы, тікбұрышты параллелепипед бейнеленген 35-40 сызбаны дайындап алып, содан кейін оларға өлшемдерін жазу арқылы жеке тапсырмалар жиынтығын алуға болады. Сонымен қатар, көпжақтарды оқып-үйрену барысында әртүрлі жұмыс кестелері мен анықтамалық кестелерді қолдануға болады. Жұмыс кестелері - бұл олардың материалдарының көмегімен оқушылардың жаңа теориялық материалдарды меңгеру бойынша да, оларды бекіту бойынша да ойлауға қатысты белсенді іс-әрекетті ұйымдастыруға болатын кестелер. Жұмыс кестелерінің көмегімен оқушыларда белгілі бір білімдер мен біліктіліктерді қалыптастыру мен бекітуді дамытуға әсер ететін көптеген жаттығуларды орындауды жүзеге асыруға болады, оқушылар арасында сауалнама жүргізуге болады, түтас сынып алдында проблемалық мәселе қоюға болады. Мысалы, пирамида ұғымын енгізу барысында пирамида, оның негізгі элементтері мен дербес жағдайлары бейнеленген кестені қолдануға болады. Анықтамалық кестелердің, яғни есте сақтап қалуға арналған кестелердің жұмыс кестелерінен айырмашылығы олардың оқушылардың көру аппараттарына ұзақ уақыт әсер етуге арналғандықтарында. Мұндай кестелер математика кабинетінде ұзақ уақыт ілініп тұрулары мүмкін. Сонымен, анықтамалық кестелердің (көрнекіліктен өзге, көп жағдайда бұл маңызды рөл атқарады) негізгі қасиеті олардың дидактикалық бағытта болуында болып табылады. Бұл кестелер оқушыларға негізгі фактілерді, формулаларды, графиктерді және т.б. жаттату мақсатында мәжбүрлі түрде әсер етуге арналған. Мұндай кестелердің мысалы ретінде көпжақтардың түрлері бейнеленген және олардың әр түрінің көлемдері мен беттерінің аудандарын есептеуге арналған формулалар көрсетілген Көпжақтардың аудандары мен көлемдерін есептеу кестесін атауға болады.
Сонымен қатар, диапозитивтер, кодопозитивтер, компьютерлік құралдар сияқты көпжақтарды оқуда (басқа тақырыптарды оқуда да) тиімді қолдануға болатын оқыту құралдарын да ұмытпау керек.
Кейде көрнекі құралдарды білімді алғаш меңгергенде уақытша тірек ретінде қарастырады. Көрнекі құралдардың рөлдерін осылай бағалаудың жақтастары модельдер бұл жағдайда оқушыларды нақты нәрселерге ғана үйретеді және сондықтан оқушылардың логикалық ойлау қабілеттерін дамытуға ықпал етпейді деп санайды. Тіпті мынадай дидактикалық ереже ұсынылады: оқушы жас ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.