Үшбұрышты пирамиданың кескінін салу

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:

Орта мектеп геометрия курсында Тетраэдр тақырыбын оқыту әдістемесі

Выпускная квалификационная работа

Избранные теоремы геометрии тетраэдра

Содержание

Введение
Глава I. Виды тетраэдров и теоремы о тетраэдрах
.1 Теоремы о тетраэдрах
§1. Теорема Менелая
§2. Теорема Чевы
§3. Свойства медиан и бимедиан тетраэдра
.2 Различные виды тетраэдров.
§1. Пифагоровы тетраэдры
§2. Ортоцентрические тетраэдры
§3. Каркасные тетраэдры
§4. Равногранные тетраэдры
§5. Инцентрические тетраэдры
§6. Соразмерные тетраэдры
§7. Правильные тетраэдры
Глава II. Тетраэдр в курсе математики средней школы
§1. Сравнительная характеристика изложения темы тетраэдр в школьных учебниках
§2. Тестирование уровня развития пространственного мышления у учеников средней школы
Введение

Интерес к изучению тетраэдра возник у человечества с древних времен и не угасает до сих пор. Это связано не только с его красотой, но и с большой практической ценностью.
Тетраэдр является одним из основных фигур стереометрии, однако его изучение в курсе средней школы недостаточно подробно. В некоторых учебниках авторы избегают самой терминологии, предпочитая называть фигуру треугольной пирамидой (и рассматривают её именно в таком ключе), а об изучении различных видов тетраэдров зачастую и говорить не приходится.
Роль задач о тетраэдрах в математическом развитии школьников трудно переоценить. Они стимулируют накопление конкретных геометрических представлений, способствуют развитию пространственного мышления, что особенно важно в процессе изучения стереометрии.
Изучению тетраэдра как школе, так и в вузах посвящено лишь небольшое количество занятий, поэтому целью дипломной работы является изучение различных видов тетраэдров, а также теорем, связанных с геометрией тетраэдра. В соответствии с целью сформулированы следующие задачи:
. Собрать сведения о тетраэдре из различных источников и привести их в систему; разобрать доказательства теорем, связанных с тетраэдром;
. Проанализировать методику изложения материала в различных школьных учебниках;
. Разработать курс занятий о тетраэдре для средней школы.
В первой главе моей дипломной работы речь пойдёт о различных видах тетраэдра и некоторых теоремах, касающихся этой фигуры. Вторая глава посвящена анализу учебного материала для средней школы по заданной теме и разработке курса занятий.

Кіріспе

Диплом жұмысының өзектілігі:Геометрия (гр.geometrіa, ge -- Жер және metrio -- өлшеймін) -- математиканың кеңістіктік пішіндер (формалар) мен қатынастарды, сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін саласы. "Жер учаскелерін өлшеу нәтижесінде -- деп жазған біздің заманымыздан бұрын 4 ғасырда өмір сүрген грек математигі Евдем, -- мысырлықтар Геометрия ғылымын шығарды". Жер өлшеу өнерін мысырлықтардан үйренген ежелгі гректер оны алғашқы кезде өз тілінде "Геометрия" деп атаған. Осы сөз кейін көптеген халықтардың тіліне еніп, ғылыми термин болып кеткен.
Геометрия - тамаша пән. Себебі, оқушының ақыл - ойын дамытуда, ойлау қабілетін жетілдіруде оның маңызы зор. Сонымен қатар, ең бастысы - ойдан ой туындатуға, әр сөздің, айтылған ойдың дәлелді болуын қадағалауға мүмкіндік береді. Дәл және нақты түрде ой тұжырымдауға, ой тізбегін саралап, талдап, одан дұрыс қорытынды жасауға үйретеді.
Геометрия пәні планиметрия және стереометрия бөлімдеріне ажыратылып оқытылады.
Соның ішінде көпжақтар тақырыбы орта мектептегі стереометрия курсының негізгілерінің бірі болып табылады.Орыс математигі Л.А.Люстерник (1899 - 1981 жж.) былай деген: Көпжақтар теориясы, оның ішінде дөңес көпжақтар - геометрияның өте қызықты бөлімдерінің бірі. Шынында да, геометриялық денелердің үлкен бір тобын көпжақтар құрайды.
Жұмыстың мақсаты: Пирамида және қиық пирамида тақырыбының теориялық негіздерін ашып, оған қатысты анықтамалар мен теоремалардың мән - мағынасына талдау жасау, пирамида және қиық пирамида тақырыбын оқыту әдістемесін қарастыру.
Зерттеудің нысаны: Мектеп курсында геометрия пәнін оқыту.
Жұмыстың практикалық құндылығы: Жұмыстағы пирамида және қиық пирамида тақырыбының теориялық негіздерін және әдістемесін мектеп курсының және жоғарғы оқу орындарының мұғалімдері қолдана алады.
Ғылыми мәселенің қазіргі кездегі шешу жағдайын бағалау. Мектеп геометрия курсындағы пирамида және қиық пирамида тақырыбын оқытуда түрлі мәселелер кездесіп жатады. Солардың теориялық мәселерелін анықтап, оқып үйрену керек.
Зерттеудің пәні:Жоғары сыныптардағы пирамида және қиық пирамида тақырыбы.
Зерттеудің міндеті:
көпжақ, пирамида және қиық пирамида анықтамасын, жалпы
қасиеттерін оқыту әдістемесін қарастыру;
пирамида және қиық пирамида көлемін,бүйір бетінің және толық бетінің ауданын табуды үйрету;
іштей және сырттай сызылған пирамидаларды кескіндеуді талдау;
геометриялық фигуралардың кескінін салуды қарастыру;
пирамида және қиық пирамида тақырыптарына есептерді шығара білуге баулу.
Ғылыми жаңалығы:Мектеп геометрия курсындағы пирамида және қиық пирамида тақырыбын оқытудың теориялық негіздемелерін, оқыту әдістемесін оқып-үйрену. Пирамида және қиық пирамида ұғымдарын анықтаудың әртүрлі әдебиеттердегі салыстырмалы талдауын жасау.
Дипломдық жұмыстың теориялық және методологиялық негіздері: Дипломдық жұмыстың теориялық және методологиялық негізін математик ғалымдардың, әдіскерлердің пирамида және қиық пирамиданы оқытуға байланысты ғылыми - әдістемелік еңбектеріндегі қағидалар мен ұсыныстар құрайды.

I Тетраэдр тақырыбының теориялық негіздері
1. Көпжақ және оның түрлері

1 - анықтама:Көпбұрыштардан тұратын және қандай да бір геометриялық денені шектейтін бетті көпжақты бет немесе көпжақ деп атайды. Көпжақты құрайтын көпбұрыштар оның жақтары деп аталса, жақтардың қабырғалары - көпжақтың қырлары, ал қырлардың ұштары төбелері деп аталады.
Көпжақтың түрлері:
oo тетраэдр;
oo октаэдр;
oo икосаэдр;
oo додекаэдр;
oo куб (гексаэдр);
oo призма;
oo параллелепипед;
oo пирамида.[2]
Куб (гексаэдр)
Икосаэдр
Додекаэдр
Тетраэдр
Параллелепипед
Октаэдр
Пирамида
Призма

Көпжақтардың ерекше қызықты түрінің бірі - пирамида. Пирамида тақырыбын қозғағанда Мысыр пирамидаларын атамай кету мүмкін емес. Олар тек математиктерді ғана емес, сонымен қатар физиктерді, тарихшыларды, т.б. қызықтырып келеді. Оларды зерттеумен ғалымдар жүздеген ғасырлар бойы айналысуда. Сонымен пирамида дегеніміз не?
2 - анықтама: Пирамида(грекше pyramis - зәулім)деп бір жағы кез келген көпбұрыш, ал қалған жақтары төбелері ортақ үшбұрыштардан тұратын көпжақты атайды.
С
В
А
О
Алдымен пирамиданың ең қарапайым түрі - үшбұрышты пирамидаларды қарастыралық.

1-сурет. Кез келген үшбұрышты пирамида

1-суретте О, А, В, және С төбелерімен берілген. О нүктесі пирамиданың төбесі деп аталады. Пирамиданың ОАВ, ОВС, ОСА, АВС жақтары - үшбұрыштар.
АВС жағын пирамиданың табаны деп атайды.ОА, ОВ, ОС кесінділері - пирамиданың қырлары, АВ, ВС, СА, - пирамиданың табан қабырғалары.
Пирамиданың табанында жатқан үшбұрыштың түріне қарай пирамида әртүрлі көрінуі мүмкін. Мысалы, 2.1-суретте тікбұрышты пирамида бейнеленген, ал 2.2-суретте үшбұрышты көлбеу пирамида бейнеленген.
Бұл атаулар пирамиданың биіктігінің, дәлірек айтқанда, биіктігінің табаны қалай, қайда орналасқандығымен байланысты. Үшбұрышты пирамиданың биіктігін нүктеден жазықтыққа түсірілетін перпендикуляр түсінігі арқылы анықтауға болады. 2.1-суреттен тік пирамида биіктігінің табаны пирамида табанының ішкі нүктесі болатынын көреміз. Көлбеу пирамида биіктігінің табаны пирамида табанынан тысқары жатыр (2.2 - сурет). Пирамиданың биіктігі дегеніміз - оның төбесінен табан жазықтығына түсірілетін перпендикуляр немесе осы перпиндикулярдың ұзындығы.
2.3-суретте дұрыс үшбұрышты пирамида бейнеленген. Ондай пирамиданың табанында дұрыс үшбұрыш жатады, ал оның барлық бүйір жақтары өзара тең болатын теңбүйірлі үшбұрыштар. Бұл жағдайда биіктіктің табаны пирамида табанының центіріне дәл түседі (табанының центрін табанының төбелерінен бірдей қашықтықта орналасқан нүкте ретінде анықтауға болады).

М
С
В
А
О
А
С
В
К
О
D
С
В
А

2-сурет. Үшбұрышты пирамиданың түрлері
Геометрияда пирамиданың барлық жақтары да негізі болатын жеке түрлері жиі қарастырылады. Мұндай пирамидаларды тетраэдрлер деп атайды. Ол "төртжақты" деген мағына білдіреді. Тетраэдрдің 4 жағы, 4 төбесі және 6 қыры болады.
Үшбұрышты пирамидалар (жазықтығы үшбұрыштар тәрізді) қатаңдық қасиетіне ие. Пирамидалар - "қатаң" геометриялық фигуралар, басқаша айтқанда, олардың пішінін өзгертуге болмайды.

Жалпы, көлем дегеніміз геометриялық денелердің кеңістіктен алатын бөлігін сипаттайтын шама. Қарапайым жағдайда, көлем дене ішіне сиятын бірлік кубтардың санымен өлшенеді. [3.13]
Теорема 1: Пирамиданың көлемі табанының ауданы мен биіктігінің үштен бір көбейтіндісіне тең:.
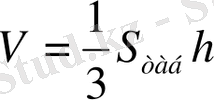Дәлелдеуі:Теореманы әуелі үшбұрышты пирамида үшін, одан кейін кез келген пирамида үшін дәлелдейік.
1.Табанының ауданы S, биіктігі h, ал көлемі V болатын OABC үшбұрышты пирамиданы қарастырайық. Ox осін жүргізіп (18.1 - суретте OM - пирамиданың биіктігі ) пирамиданы Ox осіне перпендикуляр жазықтықпен, демек, табан жазықтығына параллель жазықтықпен қиғандағы A'B'C' қимасын қарастырайық. Бұл жазықтықтың Ox осімен қиылысу M' нүктесінің абсциссасын x деп, ал қимасының ауданын S(x) арқылы белгілейік. S(x) функциясын S, h және х арқылы өрнектейміз. A'B'C' пен АВС үшбұрыштары ұқсас. Шынында да, A'B'\\ АВ, сондықтан ОВА~О A'B'. Олай болса, . 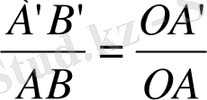Тікбұрышты О A'M' пен ОАМ үшбұрыштары да ұқсас (оларға О сүйір бұрышы ортақ). Сондықтан 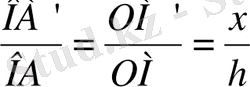. Сонымен: 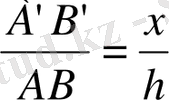. Осы сияқты 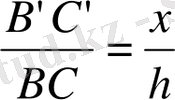және 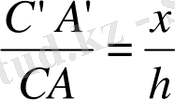екені дәлелденеді.
S'''
S''№№№э№
S'№№№э№
һ№№№э№
С'
В'№№№э№
А'№№№э№
һ
О
х
М
С
В
А

М'

1 2
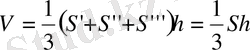
18 - сурет. Үшбұрышты және бесбұрышты пирамида
A'B'C' пен АВС үшбұрыштары ұқсас, ұқсастық коэффициенті. Олай болса, 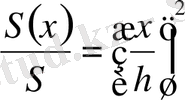, бұдан 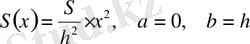болғанда дененің көлемін есептеудің негізгі формуласын пайдалансақ,
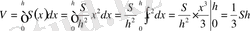[1]
2. Енді теореманы табанының ауданы S, биіктігі h болатын кез келген пирамида үшін дәлелдейік. Мұндай пирамиданы h биіктігі ортақ үшбұрышты пирамидаларға бөлуге болады (18.2 - суретте бесбұрышты пирамиданы бөлу көрсетілген). Әрбір үшбұрышты пирамиданың көлемін дәлелденген формула бойынша есептеп, оларды қосамыз. Жақшалар сыртына ортақ 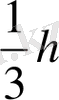көбейткішін шығарып, жақшалар ішінде үшбұрышты пирамидалардың табандары аудандарының қосындысын, демек, бастапқы пирамида табанының S ауданын аламыз. Олай болса, бастапқы пирамиданың көлемі 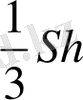көбейтіндісіне тең. Теорема дәлелденді. [1.165]
Ал, аудан дегеніміз жазық геометриялық фигуралар мен беттердің сандық сипаттамаларының бірі. Қарапайым жағдайда, аудан жазық фигураның ішін толтырып тұратын бірлік квадраттардың санымен анықталады. [4]
Дұрыс пирамиданың бүйір бетінің ауданын есептеп шығаруға арналған формуланы қорытып шығаралық (20 - сурет). Ол үшін пирамиданың бүйір жағының ауданын барлық бүйір жақтарының санына көбейтеміз:

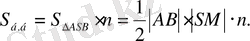
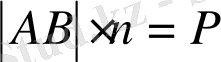және 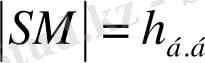депбелгілеп, мына формуланы табамыз:

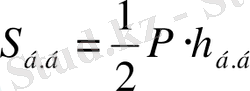
Мұндағы P - дұрыс пирамида
табанының периметрі, -
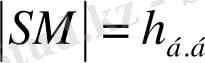апофемасының ұзындығы.
Теорема 2:Дұрыс пирамиданың
бүйір бетінің ауданы оның
табанының периметрі мен
апофемасының көбейтіндісінің
жартысына тең болады. [5]

Мысалы: Үш бұрышты пирамиданың табан қабырғалары 6, 10, 14-ке тең. Табанындағы әрбір екі жақты бұрышы 300 -қа тең. Пирамиданың бүйір бетінің ауданын табыңыз (21 - сурет).
Берілгені: SABC - үшбұрышты пирамида.
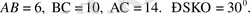
Табу керек:
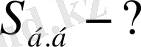
Ш е ш у і: Пирамиданың биіктігі оның табанына іштей сызылған шеңбердің центріне проекцияланады.
1)
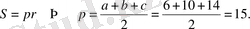
2)
21 - сурет
S
В
К
О
C
А
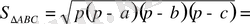
3)
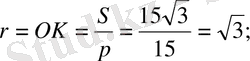
4) SКO-нан:

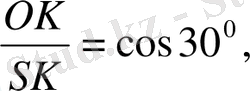
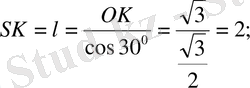
5)

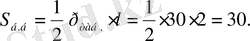
Демек, пирамиданың бүйір бетінің ауданы 30-ға тең.
(Жауабы: 30.)
Пирамида бетінің ауданысол пирамиданың бүйір бетінің ауданына табанының ауданын қосқанға тең.
Мысалы: Дұрыс үшбұрышты пирамида биіктігі h - қа тең, ал табан қабырғасындағы екі жақты бұрыш 450 -қа тең. Пирамида бетінің ауданын табыңдар (22 - сурет).
Берілгені: SABC - дұрыс үшбұрышты пирамида.
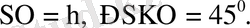
Табу керек:
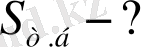
Ш е ш у і: Дұрыс үшбұрышты пирамиданың биіктігі оның табанына іштей сызылған шеңбердің центріне проекцияланады.
1.Табаны дұрыс үшбұрыш болғандықтан OK = ON = OM = r болады.
2. тік бұрышты үшбұрыш және болғандықтан SO = OK = h.
22 - сурет
M
N
K
S
О
С
В
А
3. 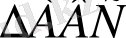- дан:
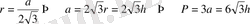
4.
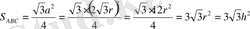
5.
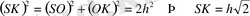
6.
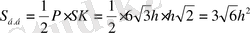
7.
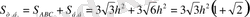
Демек, пирамида бетінің ауданы
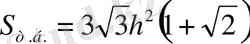-ға тең.
(Жауабы: )

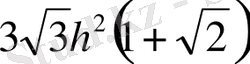2 Іштей және сырттай сызылған үшбұрышты пирамидалар

Дұрыс пирамидаға сырттай сызылған шар. Кез келген дұрыс пирамидаға сырттай шеңбер сызуға болады. Шар центрі пирамиданың биіктігін қамтитын түзуде жатады және бүйір қабырғасы пирамиданың бүйір қыры, ал биіктігі пирамиданың биіктігі болатын тең бүйірлі үшбұрышқа сырттай сызылған шеңбердің центрімен беттеседі (27.1 - сурет).
Дұрыс пирамидаға іштей сызылған шар. Кез келген дұрыс пирамидаға іштей шар сызуға болады. Шар центрі пирамиданың биіктігінде жатады және бүйір қабырғасы (бүйір жағының биіктігі) пирамиданың апофемасы, ал биіктігі пирамиданың биіктігі болатын тең бүйірлі үшбұрышқа іштей сызылған шардың центрімен беттеседі. Шардың радиусы осы шеңбердің радиусына тең (27.2 - сурет).

1 2

27 - сурет. Шарға іштей және сырттай сызылған пирамидалар

1.Шардың радиусы R, пирамида биіктігі H және пирамиданың табанына сырттай сызылған шеңбердің радиусы r мынадай қатынаспен байланысқан (28.1 - сурет):

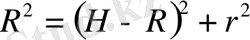
Бұл қатынас болған жағдайда да орындалады.
2. Шардың радиусы R, пирамида биіктігі H және пирамиданың табанына іштей сызылған шеңбердің радиусы r мынадай қатынаспен байланысқан (28.2 - сурет): [7]

R
H
r
H
R
r

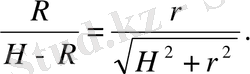
1 2

28 - сурет. Шарға іштей және сырттай сызылған пирамидалардың қимасының көрінісі

3 Геометриялық фигураларды кескіндеудің анықтамасы және
оған қойылатын талаптар

А н ы қ т а м а 7: Фигураның кескінідеп оның параллель проекциясына ұксас фигураны айтамыз.
Геометриялық есептерді шығару барысында қолданылатын фигура кескіндері еркін параллель проекциялау негізінде салынады. Яғни, берілген фигураныпроекция жазықтығына қатысты орналасуы мен проекция бағыты анықталмайды. Стереометрияда әртүрлі жазықтықтарда жатқан жазықфигуралардын бәрін бір сызба жазықтығына кескіндеуге тура келеді. Мысалы, параллелепипедті кескіндеу кезінде, оның алты түрлі жазықтықтарда жатқан жақтарын (параллелограмдарды) бір жазыктыққа кескіндейміз.
Олай болса, кеңістік фигурасын кескіндеу үшін, біріншіден, жазық фигураларды кескіндеу мәселесіне тоқталу керек. Параллель проекциялау әдісін пайдаланып кескіндеу барысында, берілген фигура жазықтығы мен бейнелеу жазықтығы параллель болмаса, онда жазық фигура кескіндеу кезінде өзгеріске ұшырайтыны түсінікті.
Жазық фигураларды кескіндеу теориясы мынадай екі теоремаға негізделген.
Теорема 3: (Бар болудың бірінші теоремасы). Берілген қандай да болмасын үшбұрышты, кез келген үшбұрыш етіп кескіндеуге болады.
Теорема 4: Егер 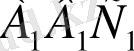үшбұрышының кескіні берілген болса, онда осы үшбұрыш жатқан жазықтықтың әрбір нүктесінің кескіні де бір мәнді анықталған болады.
Олай болса, осы теоремалар негізінде тең қабырғалы үшбұрыштың, тең бүйірлі үшбұрыштың және тікбұрышты үшбұрыштың кескіндері кез келген үшбұрыш болатынын көреміз. Сондай-ақ, үшбұрыш жазықтығының әрбір нүктесінің кескіні бірмәнді анықталады. Мысалы,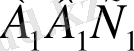теңбүйірлі үшбұрышы берілген болсын (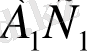=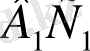). Осы үшбұрышты және оның 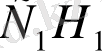биіктігін кескіндейік.
Шешуі: 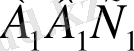үшбұрышының кескіні 3-теоремаға сәйкес кез келген АВС үшбұрышы болады. Ал 4-теоремаға сәйкес 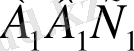үшбұрышының әрбір нүктесінің кескіні АВС үшбұрышы арқылы бірмәнді анықталады. Демек, осы үшбұрыштың 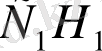биіктігін енді бұлай еркін түрде кескіндей алмаймыз. 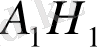=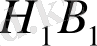болғандықтан және кескіндеу параллель проекциялау негізінде орындалатындығын ескеріп, параллель проекциялаудың қасиетіне сәйкес (параллель проекциялауда, бір түзудің немесе параллель түзулердің бойында жатқан кесінділердің қатынасы сақталады) Н нүктесі АВ кабырғасының ортасы болады (29-сурет).

29-cурет. Параллель проекциялау көрінісі

Н

B
A

C

В

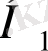
Осы теоремалар негізінде басқа да жазық фигураларды кескіндеуге тоқталайық.
Мысалы:А′В′С′D′ параллелограмын кескіндеу керек болсын. Шешуі: Берілген параллелограмнан А′В′С′ үшбұрышын алып, 3-теорема бойынша оның кескіні АВС үшбұрышын аламыз. Параллелограмнын төртінші төбесінің Dкескні параллель проекциялаудың қасиеттері бойынша салынады. Яғни, А'В'С′D′ жәнеВ'С′А'D'болғандықтан, оған сәйкес АВСD,ВСAD болады.
Демек, кез келген параллелограмның кескіні паралелограмм болатындығы шығады.
А′В′С′ теңбүйірлі үшбұрышы мен оның С'Н' биіктігін кескіндеу реті.
Олай болса, кез келген көпбұрышты (жазық фигураны) кескіндеу үшін, оныңқұрылымынан қандай да бір үшбұрыш бөлініп алынып, 3-теорема
негізінде кескінделіп, ал басқа төбелерінің кескіндері параллель проекциялаудың қасиеттері негізінде салынады екен. Сонда кескіндеукезінде, жазық фигура құрамынан таңдалып алынған үшбұрыштың төбелері базистік нүктелер деп аталады.
Бұдан мынадай қорытындылар жасаймыз: Үшбұрыштың кескіні - кез келген үшбұрыш, параллелограмның, тіктөртбұрыштың, ромбының және квадраттың кескіндері - параллелограмм, ал трапецияның кескіні кез келген трапеция болады. Сондай-ақ, дұрыс бесбұрыштың кескіні кез келген бесбұрыш, дұрыс алтыбүрыштың кескіні - кез келген алтыбұрыш т.с.с. Ал шеңбердің кескіні - эллипс.
Ал стереометриялық фигураларды кескіндеу Польке-Шварц теоремасына (бар болудың екінші теоремасы) негізделеді.
Теорема 5:А′В′С′D′ тетраэдрінің қандай да бір жазықтықтағы проекциясы ретінде диоганалдарымен бірге алынған АВСD төртұрышын қарастыруға болады.
Мұндай еркін параллель проекциялау негізінде алынған кескіннен түпнұсқаны қайта құрастыру мүмкін емес, мектеп геометриясында оны орындау талап етілмейді.
Орта мектептегі есеп шығару барысында орындалатын проекциялық сызбалардағы фигуралар кескініне мынадай талаптар қойылады:
1 Кескін дұрыс болуы керек, яғни түпнұсқаның параллель проекциясына ұқсас фигураны беруі керек.
2 Кескін мүмкіндігінше көрнекі болуы, яғни түпнұсканың формасы туралы кеңістіктік түсінік беретіндей болуы кажет.
3 Кескін оңай орындалатын болуы, яғни салу ережелері барынша қарапайым болуы керек. Көмекші салулардың көптігі, тек есептің мазмұнын түсінуді қиындатады.
Дұрыс кескін және көрнекі кескін әр түрлі ұғымдар. Кескіннін дұрыстығы қатаң анықталатын математикалық ұғым болып табылады, ал кескіннің көрнекілігі ұғымы кескінделген фигураны әркімнің жеке кабылдау ерекшеліктеріне байланысты болғандықтан, субъективті ұғымдар қатарына жатады.
Демек кескін дұрыс болуы үшін оны параллель проекцияның касиеттеріне сәйкес салу жеткілікті екен. Кескіннің дұрыстығы ұғымы, оның позициялық толықтығы (немесе жай ғана толықтығы) ұғымымен де тығыз байланысты. Ф0 фигурасының проекциялық сызбасында оның әрбір А нүктесі бейнеленген болса, онда фигураның кескіні толық деп аталады. Мысалы, 30 а,ә-суреттердегі куб кескіндері толық емес. Өйткені, куб кескініндегі көп элементтер беттесіп кеткен. Егер Ф фигураның кескіні толық болса, онда фигура кескінінде кез келген позициялық есеп орындалады. Яғни, дербес жағдайда фигураның кез келген жазықтықпен қиғандағы қимасын салуға болады. [17]
Стереометрия курсын оқу барысында әрбір оқушы сызбалар салады. Бірақ көп жағдайда олар сызбаларды ешкандай ережесіз орындайды. Көбінесе оқушы оқулықтағы сызбалар мен мұғалімнің тақтада көрсеткен сызбаларын көшіреді. Берілген фигураны оны кескіндеуге қойылатын барлық талаптарды қанағаттандыратындай етіп салу мәселелеріне келгенде, кейде мұғалімдердің өздері де кескіндеу ережелерін жетік біле бермейтіндігін байқаймыз. Мысалы, дұрыс үшбұрышты пирамида 31,а-суреттегідей кескінделген болсын. Бұл суретке қарай отырып, алынған пирамида барлық талаптарға сай сияқты көрінеді. Ал енді осы сызбада пирамида биіктігін жүргізу керек болсын.
Дұрыс үшбұрышты пирамида биіктігі табаньшдағы үшбұрыштың медианаларының қиылысу нүктесіне түсетіндігін ескерсек 31,ә-суреттегідей дұрыс, бірақ көрнекі емес кескін аламыз.

::
31-сурет. Үшбұрышты пирамиданың көрнекі емес кескіні
)
ә)

Сондықтан, дұрыс үшбұрышты пирамиданы кескіндеу мынадай ретпен жүргізіледі. (32-сурет).
1) Табанындағы үшбұрышты кескіндеу (32,а-сурет);
2) Осы үшбұрыштың медианаларының қиылысу нүктесін салу (32,ә-сурет);
3) Осы нүктеден биіктік тұрғызу (32,б-сурет);
4) Биіктік төбесімен табанындағы үшбұрыш төбелерін қосу. (32, в-сурет);
б)
в)

)
ә)
::
::
::
::
::
::
::
::
::
::
32-сурет. Дұрыс үшбұрышты пирамиданы кескіндеу реті

Кескіннің дұрыстығы ұғымымен, тағы да оның метрикалық анықталғандығы ұғымы тығыз байланысты. Ф0 фигурасының кескіні арқылы, оны ұқсасқа дейінгі дәлдікте қайта құрастыру мүмкін болса, онда оның кескіні метрикалық анықталған болып табылады.
Есептің шартында түпнұсқаны ұксасқа дейінгі дәлдікте кұруға мүмкіндік беретін шарттар берілген болса, фигураның кескінін шартты кескін деп атайды. Орта мектептің математика сабақтарында дәл осындай шартты кескіндер қолданылады.
Проекциялық сызбада орындалатын салулар позициялық және метрикалық болуы мүмкін. Позициялық салуларға түпнұсқаны параллель проекциялау негізінде сақталатын қасиеттері жататын болса, метрикалық салуларға, әдетте, түпнұсқаның параллель проекциялауда сақталмайтын қасиеттері жатады.
Кейбір есептер алғашында метрикалық есептер сияқты көрінгенімен, шындығында позициялық болуы мүмкін. Мысалы, үшбұрыштың биіктігін салу жалпы жағдайда метрикалық салу, өйткені параллель проекциялағанда түзулердің перпендикулярлығы сақталмайды. Егер түпнұсқада А′В′С′үшбұрышының А'В' және В'С'қабырғалары тең болса, онда туннұсқада В′D′ биіктігі, әрі медиана болады, ал параллель проекцияларында медиана болатын кесіндінің қасиеті сақталады. Олай болса, бұл қарастырып отырған есептегі биіктікті салу позициялық салу болып табылады.
Толық кескіннің метрикалық анықталғандығын негіздеу үшін фигуранын аффиндік және метрикалық қасиеттерін ажырата білу қажет. Олардың кейбіріне тоқталайық:
Аффиндік (параллель проекциялау нәтижесінде сақталатын) қасиеттер:
1. Фигураның нүкте, түзу, жазықтық болу қасиеттері;
2. Фигураның қиылысқан болу қасиеттері;
3. Кесіндіні берілген қатынаста бөлу;
4. Түзулердің, жазықтықтардың, түзу мен жазықтықтың параллель болу қасиеттері;
5.Фигураның үшбұрыш, параллелограм, трапеция болу қасиеттері;
6.Параллель кесінділердің ұзындықтарының қатынасы;
7. Екі фигураның аудандарыныңқатынасы және т.б.
Метрикалық (параллель проекциялауда сақталмайтын, бірақұқсас түрлендіруде сақталатын) қасиеттер:
1. Өзара бұрыш кұрайтын (дербес жағдайда перпендикуляр болатын) түзулер (жазықтықтар, түзулер мен жазықтықтар);
2. Параллель емес түзулердің ұзындықтарының қатынасы;
3. Түзулер арасындағы бұрыштар шамаларының қатынасы (дербес жағдайда, бұрыштың биссектрисасы болатын түзудің қасиеттері);
4. Екі жақты бұрыштар шамаларының катынастары;
5. Түзулер мен жазықтықтар арасындағы бұрыштардың қатынастары және т.б.
Демек, мысалы, түпнұсқада табаны квадрат болатын дұрыс төртбұрышты призманы кескіндегенде табаны кез келген параллелограмм болады. Себебі оның іргелес қабырғаларының перпендикулярлығы метрикалық қасиетке, ал қарама-қарсы қабырғаларының параллельдігі аффиндік қасиетке бағынады. Олай болса, кез келген параллелограмм - параллелограмның

C
S
В

K
D
34-сурет
да, төртбұрыштың да, ромбының да және сондай-ақ квадраттың да кескіні болады.
Мысалы: Үшбұрышты пирамиданың бүйір жақтарының бірі табан жазықтығына перпендикуляр. Осы бүйір жағы мен табаны дұрыс үшбұрыштар. Пирамиданың кескін, ретінде диагональдармен қоса алғанда АВСDтөртбұрышын алып, кескіннің параметрлер санын анықтайық.
Шешуі: Пирамида табанындағы дұрыс үшбұрыштың кескіннің кез келген үшбұрыш болып алынуынан екі параметр жаратылады (34-сурет). Нақтырақ айтсақ, мұнда АВ=ВС=АС және метрикалық қасиеттері сақталмай отыр. Осы сияқты бір бүйір жағының да дұрыс үшбұрыш екендігін ескерсек, оған да екі параметр жаратылады және осы салынғанүшбұрыштардың жазықтықтары түпнұсқада перпендикуляр екендігін ескерсек кескінге тағы да бір метрикалық шарт қойылады, яғни тағы бір параметр жаратылады. Олай болса берілген пирамиданың кескініне бес параметр жаратылған, яғни кескіннің параметрлік саны р=5, сондықтан бұл кескінде бұлардан басқа ешқандай метрикалық салуларды еркін орындауға болмайды. Енді осы SАВС пирамиданың кескінінде SАС жағының SК биіктігін салу қажет болсын. Ол үшін қосымша салулар жүргізу қажет. АВС үшбұрышының ВN медианасын жүргіземіз. АВС дұрыс үшбұрыш болғандықтан ВN әрі биіктік болады, яғни ВNАС. Осыған ұқсас SАВ үшбұрышының SD медианасын, әрі биіктігін жүргіземіз. Мұндағы SDАВ және SD(АВС). DКВN жүргіземіз, сонда DКАС болады. S нүктесі мен К нүктесін кесіндімен қосамыз. SD кесіндісі АВС жазықтығына перпенднкуляр болғандықтан, DК оның АВС жазыктығындағы проекңиясы және DКАС екендігін ескерсек үш перпендикуляр туралы теорема бойынша SКАС болатындығын көреміз. Міне көріп отырғанымыздай, SК биіктікнің табаны К нүктесі АС қабырғасының бойынан жалғыз түрде анықталады, демек SК биіктігі де жалғыз түрлі анықталып отыр.
Көпжақтар кескініне қойылатын талаптарды мына төмендегідей шартты схема түрінде бейнелеуге болады.[13]

1-кесте. Көпжақтар кесікініне қойылатын талаптар.[4]
Дұрыс
Көрнекі
Толық
Позициялық қасиеттерге ие
Метрикалық қасиеттерге ие
Метрикалық анықталған
Оңайорындалатын
Көпжақ кескін
35-сурет
::
B
C
A
S
O
::
A
В
С
S
O
::
)
B
C
A
S
O
B
C
A
S
O
ә)
б)
в)
г)
4 Пирамиданың кескінін салу. Пирамидаға берілген позициялық есептер. Толық және толымсыз кескіндер.
Оның кескіні болып, пирамида-түпнұсқаның табанын кескіндейтін көпбұрыш пен пирамиданың бүйір жақтарын кескіндейтін ортақ төбесі бар бірнеше көпбұрыштан тұратын фигура болады. Чертежде табанының кескіні жазықтықтағы көпбұрыштың проекциялары туралы айтылғандар ескерілетіндегі түсінікті.
Үшбұрышты пирамиданы кескіндеу
Үшбұрышты пирамиданы кескіндеу есебі толығымен бар болудың екінші теоремасы негізінде шешіледі. Шындығында, кез келген үшбұрышты пирамиданың кескіні ретінде бейнелеу жазықтығында диагональдарымен қоса алынған төртбұрышты алуға болады. Мысалы, бүйір қырлары табан қырларына қарағанда екі есе үлкен болатын дұрыс үшбұрышты пирамиданың кескінінсалу қажет болсын. Мына төмендегі 35-суреттегі пирамида кескіндерінің барлығы дұрыс және оңай орындалатын болғанымен, олардың барлығы көрнекі болып табылмайды.
35, а-суреттегі SO биіктігі вертикал емес түзумен кескінделген, бұл берілген
пирамиданы оқушылар көлбеу пирамида түрінде қабылдауы мүмкін. "ә"-суреттегі пирамида кескіні көрнекі емес. "в"-суреттегі пирамида кескіні "толық емес",пирамида биіктігі SС қырымен беттесіп кеткен. "б"-суреттегі үзік сызықпен көрсетілмеген қырлары, оқушылардың пирамида кескінін дұрыс қабылдауына мүмкіндік екі есе үлкен болатын пирамида туралы түсініктен қайта оқушыларға дұрыс пирамида туралы түсінік береді. Берілген пирамида туралы толық түпнұсқаны елестетуге мумкіндік беретін "г" суреттегі пирамида кескіні болып табылады.[15]
Бұл суреттегі әрбір пирамида кескіндеріндегі SО кесіндісі шындығында пирамида биіктігінің кескіні болады. Бірақ ол "а"-суретте вертикал болмағандықтан, "ә"-суретте SС қырымен беттескендіктен көрнекі емес деп есептеледі. Ал мұндай көрнекі емес кескіннің алынуының себебі, "Бар болудыңекінші теоремасы" тікелей пайдаланылып, базистік төрт нүктенің бірден таңдалып алынуыңда болып отыр .
Олай болса, көрнекі кескін алу үшін пирамида кескінін салу ретін дұрыс
тандау қажет екен. Сондықтан біріншіден пирамиданың табанындағы АВС үшбұрышының кескіні салынуы қажет (36,а-сурет). Бұл үшбұрышта пирамида биіктігінің табаны О нүктесі салынады (36,ә-сурет). Осы О нүктесі арқылы вертикал ОР түзуін түрғызамыз (36, б-сурет). Осыдан кейін барып қана төртінші базистік S нүктесін ОР түзуінің бойынан саламыз. S нүктесін А, В, С нүктелерімен қесіңділер арқылы қосып, пирамида салынады (36,в-сурет).
Жоғарыда көрсетілген рет бойынша орындалған сызба дұрыс, оңай орындалатын және көрнекі кескін алуға мүмкіндік береді.

B
C
A
::
::
::
O
B
C
A
S
::
::
::
O
B
C
A
S
::
::
::
O
B
C
A
36-сурет. Үшбұрышты пирамиданың кескінін салу
а)
б)
ә)
в)

10-есеп. Бүйір қырларының ұзындықтары өзара тең, ал табанында тікбұрышты үшбұрыш жататын үшбұрышты пирамиданың кескінін салу керек.
::
38-сурет. Теңбүйірлі үшбұрышты пирамида
В

S
O
C
Шешуі: Есеп шарты бойынша SO биіктігі пирамида табанындағы АВС үшбұрышының АВ гипотенузасының ортасына түседі. SAB жағы сызба жазықтығына параллель деп есептеуге болады. Олай болса, SAB сызбада тең бүйірлі үшбұрыш; С нүктесін кез келген жерден алуға болады (38-сурет).

Орта мектеп геометрия курсында Тетраэдр тақырыбын оқыту әдістемесі

1.1 Тетраэдр туралы теоремалар

§1. Менелай теоремасы
Үшбұрыш үшін Менелай теоремасы.
А1 және С1 нүктелері АВС үшбұрышының ВC және АC қабырғаларында, В1 нүктесі осы үшбұрыштың АС қабырғасының созындысында жатсын. А1, В1, С1 нүктелері бір түзудің бойында жатулары үшін теңдеуі орындалуы қажетті және жеткілікті (Сурет 1).

Сурет 1. Үшбұрыш үшін Менелай теоремасы

Дәлелдеу. Бірінші қажеттілігін дәлелдейік. А1,В1,С1 нүктелері l түзуінде жатсын және AA0=h1, CC0=h3 - сәйкесінше А, В, С түзулерінен l түзуіне түсірілген перпендикулярлар болсын. АА0С1 және ВВ0С1 үшбұрыштарының ұқсастығынан аламыз.
Осылайша, басқа ұқсас үшбұрыштар жұбын қарастыра отырып ; аламыз. Алынған пропорцияларды көбейту арқылы талап етілген теңдеуге келеміз.

Сурет 2. Үшбұрыш үшін Менелай теоремасын дәлелдеу

Енді жеткіліктілігін дәлелдейміз. ВС, АС, АВ түзулерінде жататын А1, В1, С1 нүктелері орындалатындай болсын. А1, В1, С1 нүктелері бір түзудің бойында жататынын дәлелдейміз.
А1В1 түзуін жүргіземіз және С1 нүктесінің сол түзуге тиісті екенін дәделдейміз. Олай емес деп алайық. А1В1 түзуінің АВ түзуіне параллель емес екенін байқаймыз. Т - А1В1 және АВ қиылысу нүктесі болсын, онда (1). (1) тепе-теңдігі мен шартынан шығады. Т және С1 нүктелері АВ кесіндісінен тыс жатқандықтан, олардың олардың сәйкестігі келесі леммадан туындайды.
1-лемма. А және В әртүрлі нүктелер болсынонда кез-келген k 0, k != 1 үшін АВ түзуінде орындалатындай, бұл нүктелердің бірі АВ кесіндісіне тиісті болатын, ал екіншісі кесіндіден тыс жататындай U және V нүктелері бар болады.
Дәлелдеу.

Сурет 3. Лемманы дәлелдеу

А нүктесін бас нүкте етіп, АВ түзуіне координаталар енгіземіз. Айқындылық үшін k 1 болсын, онда ізделінді АВ кесіндісінің ішінде жататын U нүктесінің координатасы, теңдеуін қанағаттандырады. Содан . V нүктесі AB кесіндісінен тыс жатады, теңдеуден , бұдан шығатыны . 0 k 1 жағдайы қарастырылған жағдайдан тек V нүктесін А нүктесінің сол жағынан іздеу керек екендігімен ерекшеленеді.
Менелай теоремасы қызықты стереометриялық жалпылауларға мүмкіндік береді.
Тетраэдр үшін Менелай теоремасы.

Cурет 4. Тетраэдр үшін Менелай теоремасы

Егер μ жазықтығы АВСD тетраэдрінің АВ, ВС, CD және DA қабырғаларын , А1, В1, С1, D1 нүктелерінде қиып өтетін болса, онда (2) орындалады.
Керісінше, егер тетраэдрдің АВ, ВС, СD, DA төрт қабырғасында жататын сәйкес А1, В1, С1, D1 төрт нүктелері үшін (2) тепе-теңдік орындалса, онда бұл төрт нүкте бір жазықтық бойында жатады.
Дәлелдеу.

Сурет 5. Тетраэдр үшін Менелай теоремасын дәлелдеу

h1, h2, h3, h4 - сәйкесінше А, В, С, D нүктелерінен μ жазықтығына дейінгі ара-қашықтық, онда ; ; ; .
Алынған қатынастарды көбейту ғана қалды. .
Кері теореманы дәлелдеу үшін А1, В1, С1 жазықтығын саламыз. Бұл жазықтық DA қабырғасын Т нүктесінде қиып өтетін болсын.
Дәлелдеу бойынша , ал шарт бойынша , сондықтан (және лемма бойынша) Т және D1 сәйкес келедңі. Тұжырым дәлелденді.
Үшбұрыштар үшін Чева теоремасы.

Сурет 6. Үшбұрыш үшін Менелай теоремасы

А1, В1, С1 нүктелері АВС үшбұрышының сәйкесінше ВС, АС және ВА қабырғаларында жатсын. AА1, BВ1, CС1 кесінділері бір нүктеде қиылысуы үшін (3) қатынасы орындалуы қажетті және жеткілікті. (кейде AА1, BВ1, CС1 кесінділерін чевиандар деп те атайды).
Дәлелдеу.

Сурет 7. Үшбұрыш үшін Менелай теоремасын дәлелдеу

Қажеттілігі. АА1, ВВ1, СС1 кесінділері АВС үшбұрышының ішінде М нүктесінде қиылыссын.
S1, S2, S3 арқылы АМС, СМВ, АМВ үшбұрыштарының аудандарын белгілейміз, ал h1, h2 - А мен В нүктелерінен МС түзуіне дейінгі қашықтық. Онда , осылайша , . Алынған қатынастарды көбейтіп, теореманың дұрыстығына көз жеткіземіз.
Жеткіліктілігі. А1, В1, С1 нүктелері үшбұрыштың ВС, СА, АС қабырғаларында жатсын, және (3) қатынас орындалсын. М - АА1 және ВВ1 кесінділерінің қиылысу нүктесі, ал СМ кесіндісі АВ қабырғасын Q нүктесінде қиып өтеді. Онда алдында дәлелденген бойынша . Леммадан тағы да нүктелердің Q=C1 сәйкестігі шығады. Жеткіліктілігі дәлелденді.
Енді Чева теоремасының кеңістіктегі жалпылауына көшейік.
Тетраэдр үшін Чева теоремасы.
М - АВСD тетраэдрінің ішкі нүктесі, ал А1, В1, С1 және D1 - СМD, AMD, АМВ және СМВ жазықтықтарының сәйкесінше АВ, ВC, СD және DA қабырғаларымен қиылысу нүктесі болсын. Онда (4). Керісінше: егер нүктелері үшін болса, онда АВС, ВСD1 және DAB1 жазықтықтары бір нүкте арқылы өтеді.

Сурет 8. Тетраэдр үшін Чева теоремасы
Дәлелдеу.
А1, В1, С1, D1 нүктелері бір жазықтықта (бұл жазықтық М нүктесінде қиылысатын А1С1 және В1D1 түзулері арқылы өтеді) жататынын байқайтын болсақ және Менелай теоремасын пайдалансақ дәлелдеудің қажеттілігін оңай алуымызға болады. Кері теорема кеңістіктегі Менелай теоремасының кері теоремасы сияқты дәлелденеді: А1, В1, С1 нүктелері арқылы жазықтық жүргізу керек және лемма көмегімен бұл жазықтықтың DA қабырғасын D1 нүктесінде қиып өтетінін дәлелдеу керек.

§3. Тетраэдрдің медианалары мен бимедианаларының қасиеттері
Тетраэдрдің медианасы - тетраэдрдің төбесін қарама-қарсы қырларының ауырлық центрімен (медианалардың қиылысу нүктесі) байланыстыратын кесінді.
Теорема (Менелай теоремасының қолданылуы).
Тетраэдр медианалары бір нүктеде қиылысады. Бұл қиылысу нүктесі әр мединананы төбесінен есептегенде 3:1 қатынасында бөледі.
Дәлелдеу.

ABCD тетраэдрында екі медиана DD1 және CC1 жүргізейік. Бұл медианалар F нүктесінде қиылысады. CL - ABC қырының медианасы, DL - ABD қырының медианасы, ал D1, C1 - ABC мен ABD қырларының ауырлық центрлерінің центрлері. Менелай теоремасы бойынша и . Теореманы DLD1:үшбұырышы үшін жазамыз: ; = Кез-келген басқа медиана жұптары үшін дәлелдеу осыған ұқсас жүргізіледі.
Теорема (Чева теоремасының қолданылулары).
Тетраэдрдің қиылысатын қырларының ортасын байланыстыратын кесінді бимедиана деп аталады. Бибиіктіктер (ұқсастық бойынша) деп қиылысатын қырларының жалпы перпендикулярларын деп атайды.
Теорема.
Тетраэдрдің бимедианалары да тетраэдрдің медианалары қиылысатын нүктеде қиылысады.
Дәлелдеу.
LDC үшбұрышында DC және LF кесінділері K нүктесінде қиылысады. Бұл үшбұрыштың Чева теоремасы бойынша: , яғни, , CK=KD, LK - бимедианасы.
Ескерту 1.
FL=FK. DLK үшбұрышы бойынша Менелай теоремасы: , , бұдан LF=FK.
Ескерту 2.
F нүктесі тетраэдрдің ауырлық центрі болып табылады. ,
,
демек
.

1.2 Тетраэдрдің әртүрлі түрлері

§1. Пифагорлық тетраэдрлер
Егер үшбұрыштың бір бұрышы тік болса және кез-келген қабырғаларының қатынасы орынды болса (яғни, ұқсастықты қолданғанда одан барлық ұзындықтары бар тікбұрышты үшбұрыш алынса) ол үшбұрыш пифагорлық деп аталады.
Осыған ұқсас, егер тетраэдрдің бір төбесінің бұрышы тік болғанда бұрыштары жазыңқы болса, ал кез-келген екі қырының қатынасы орынды болса (яғни бұл тетраэдрден ұқсастық бойынша бір төбесінің бұрышы тік болатын және қырларының ұзындығы тұтас болатын тетраэдр алуға болса)тетраэдр Пифагорлық деп аталады.
"Пифагорлық тетраэдрлер теңдеуін" алып көрейік, яғни үш белгісізі бар ξ, η, ζ мұндай теңдеу кез-келген Пифагорлық тетраэдр осы теңдеудің ұтымды шешімін береді, ал керісінше, теңдеудің кез-келген ұтымды шешімі пифагорлық тетраэдрді береді.

Бірінші барлық пифагорлық үшбұрыштардың сипатталу тәсілін берейік. Суретте ОАВ үшбұрышы - тікбұрышты, катеттерінің ұзындықтары а мен b арқылы, ал гипатенузаның ұзындығы - р арқылы белгіленген. санын (1) ОАВ тікбұрышты үшбұрышының параметрі деп атауға келісеміз (немесе, нақтырақ а катетіне қатысты). р2=а2+b2 қатынасын пайдаланып:

Осы теңдеулерден тік бұрышты үшбұрыштың қабырғаларының қатынастарын оның параметрі арқылы білдіретін формулаларды тікелей аламыз:

и (2).

(1) және (2) формулалардан тікелей мынадай тұжырым шығады:тікбұрышты үшбұрыш пифагорлық болуы үшін ξ саны орынды болуы қажетті және жеткілікті. Шын мәнінде, егер үшбұрыш пифагорлық болса, онда (1)-ден ξ орынды екені шығады. Керісінше, егер ξ орынды болса, онда (2) бойынша қабырғаларының қатынасы орынды,яғни үшбұрыш пифагорлық.
Енді ОАВС - бұрыштары жазыңқы болатын тетраэдр О төбесінде тік болатын тетраэдр болсын. О төбесінен шығатын қырларының ұзындықтарын a,b,с арқылы, ал қалған қыларын р, q, r деп белгілейік.

Үш тікбұрышты ОАВ, ОВС, ОСА үшбұрыштарының параметрлерін қарастырайық.

(3)

Онда (2) формула бойынша бұл тікбұрышты үшбұрыштардың қабырғаларының қатынасын олардың параметрлері бойынша беруге болады:
(4),
(5).

(4) қатынастан ξ, η, ζ параметрлерінің (6) қатынасын қатағаттандыратыны тікелей шығады. Осы пифагорлық үшбұрыштардың жалпы теңдеуі болып табылады.
(3) - (5) формулалардан тікелей мынадай тұжырым шығады: ОАВС тетраэдрі О төбесінде тік жазыңқы бұрыштармен пифагорлық болуы үшін ξ, η, ζ ( (6) теңдеуді қанағаттандыратын) параметрлерінің орынды болуы қажетті және жеткілікті.
Пифагор үшбұрышының Пифагор тетраэдрімен ұқсастығын жалғастыра отырып, Пифагор тетраэдрлері үшін дұрыс болатын тікбұрышты тетраэдрлер үшін Пифагор теоремасының кеңістіктік жалпылауын тұжырымдап, дәлелдеуге тырысайық. Бұл бізге келесі лемма көмектеседі.
Лемма 1.
Егер көпбұрыш ауданы S-ке тең болса, онда оның PI жазықтығына проекциясы тең, мұндағы φ - PI жазықтығы мен көпбұрыш жазықтығы арасындағы бұрыш.

Дәлелдеу.
Лемманың тұжырымы бір қабырғасы PI жазықтығы мен көпбұрыш жазықтығынының қиылысу сызығына параллель орналасқан үшбұрыш үшін айқын. Шын мәнінде В самом деле, бұл қабырғаның ұзындығы проекциялағанда өзгермейді, ал проекциялағанда оған түсірілген биіктіктің ұзындығы cosφ есе өзгереді.
Енді кез-келген көпбұрышты көрсетілген түрдегі үшбұрыштарға бөлуге болатынын дәлелдейміз.
Ол үшін көпбұрыштың барлық қабырғаларынан Ол үшін көпбұрыштың барлық төбелері арқылы жазықтықтардың қиылысу сызықтарына параллель түзілер жүргіземіз, содан көпбұрыш үшбұрыштар мен трапецияларға бөлінеді. Әр трапецияны кез-келген диагональ бойынша бөлі қалады.
Теорема 1 (Пифагордың кеңістіктік теоремасы).
D төбесінде жазыңқы бұрышпен АВСD тікбұрышты тетраэдрінде үш тікбұрышты жақтарының аудандарының қосындысы АВС жағының ауданының квадратына тең.
Дәлелдеу.
α - АВС мен DВС жазықтықтары арасындағы бұрыш, D' - D нүктесінің АВС жазықтығына проекциясы. Онда SΔDBC=СоsαSΔАBC және SΔD'BC=cоsαSΔDBC (1-лемма бойынша), сондықтан cоsα = . SΔD'BC = .
Осыған ұқсас теңдіктерді D'АВ және D'АС үшбұрыштары үшін алуға болады. Оларды қосып және D'ВС, D'АС мен D'АВ үшбұрыштарының аудандарының қосындысы АВС үшбұрышының ауданына тең екенін ескеріп, талап етілгенді аламыз.
Мысал.
D төбесіндегі барлық бұрыштар тік болсын; a,b,c - D төбесінен ABC жазықтығына түсірілетін жақтарының ұзындықтары. Онда
Дәлелдеу.
Тікбұрышты тетраэдр үшін Пифагор теоремасы бойынша
;
.

Екінші жағынан
(:
1=) = .

§2. Ортоцентрлік тетраэдрлер
Биіктігі әрдайым бір нүктеде - ортоцентрде ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.