Ақырлы өрістер мен алгебралық кодтау теориясы: Хэмминг, топтық, блоктық және циклдік кодтар


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М. Әуезов атындағы Оңтүстік Қазақстан Университеті
ӘОЖ-514(023 ) қолжазба құқығында
Исабеков Жандарбек Зертбекович
Ақырлы өрістер және олардың кодтау теориясында қолданылулары
7M01510 - «Математика» білім беру бағдарламасы бойынша
педагогика ғылымдарының магистрі дәрежесін алу үшін
дайындалған диссертация
Ғылыми жетекшісі:
Шымкент 2023
МАЗМҰНЫ
- АҚЫРЛЫ ӨРІСТЕР ТЕОРИЯСЫНЫҢ ҚОЛДАНУЛАРЫ . . .
- ХЭММИНГ КОДЫ . . .
- ТОПТЫҚ КОДТАР . . .
АНЫҚТАМАЛАР, БЕЛГІЛЕУЛЕР МЕН ҚЫСҚАРТУЛАР
Осы магистрлік диссертацияда сәйкес анықтамалар бойынша келесі терминдер қолданылады.
Анықтама 1. Белгілі бір ортақ қасиеттерге ие болып, белгілі бір заңдылықпен біріккен объектілер жиын құрайды. Жиындар элементтерден құралады. Жиындардың элементтері аталып беріледі немесе сол жиын элементтеріне ғана тән қасиет «белгі» көрсетіледі. Жиынды латынның бас әрпімен белгілеп, оның элементтерін фигуралық жақшаның ішіне алып жазу келісілген. Сонымен қатар, жиын элементтерінің санына қарай ақырлы және ақырсыз жиын болып бөлінеді.
Анықтама 2. Егер жиында бірде-бір элемент болмаса, оны бос жиын деп атайды.
Анықтама 3.
Егер В жиынының әрбір элементі А жиынына тиісті болса, онда В жиыны А жиынының
ішкі жиыны
деп аталады. Белгіленуі:

Анықтама 4. А жиынына да, В жиынына да тиісті элементтерден ғана тұратын жиынды А және В жиындарының қиылысуы деп атайды.
Анықтама 5. Әрбір элементі А немесе В жиындарының кем дегенде біреуіне тиісті болатын жиын А және Вжиындарының бірігуі деп аталады.
Анықтама 6.
m жолы мен n бағаны бар тікбұрышты сандар кестесі
 өлшемді матрица
деп аталады. Матрицаның құрамына кіретін сандар оның
элементтері
деп аталады.
өлшемді матрица
деп аталады. Матрицаның құрамына кіретін сандар оның
элементтері
деп аталады.
Анықтама 7. Егер матрицаның жолдарының саны оның бағандарының санына тең m=n болса, онда матрица квадрат матрица деп аталады.
Анықтама 8. Матрицаның жолдарының саны матрицаның реті деп аталады.
Анықтама 9.
А
матрицасының анықтауышы
 деп
деп
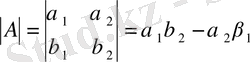 санын атайды.
санын атайды.
Анықтама 10.
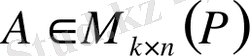 матрицасының
матрицасының
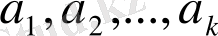 жолдарын
жолдарын
 кеңістігінің, ал
кеңістігінің, ал
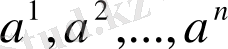 бағандарын
бағандарын
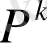 кеіңістігінң векторлары ретінде қарастырып,
кеіңістігінң векторлары ретінде қарастырып,
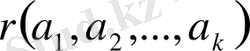 рангін А матрицасының
жолдар рангі
, ал
рангін А матрицасының
жолдар рангі
, ал
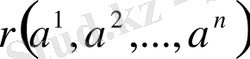 рангін А матрицасының
бағандар рангі
деп атаймыз.
рангін А матрицасының
бағандар рангі
деп атаймыз.
Анықтама 11.
S - кез-келген жиын және
 жиыны
жиыны
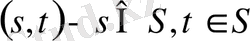 жұптарынан тұратын жиын. Онда
жұптарынан тұратын жиын. Онда
 жиынын
жиынын
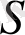 жиынына бейнелейтін кез-келген бейнелеуді
жиынына бейнелейтін кез-келген бейнелеуді
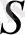 жиынындағы
(бинарлық) операция
деп атаймыз.
жиынындағы
(бинарлық) операция
деп атаймыз.
Анықтама 12.
Кез-келген
 жиынын «
жиынын «
 » операциясы бинарлық операция болса және келесі шарттар орындалса:
» операциясы бинарлық операция болса және келесі шарттар орындалса:
- «» операциясы ассоциативті, яғни
- Gжиынындаебірлік элемент бар болса, яғни
- Gжиынындаа-1кері элемент бар болса элемент бар болса,
яғни

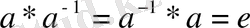 орындалса
орындалса
онда
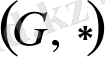 жиыны
топ
деп аталады.
жиыны
топ
деп аталады.
Анықтама 13.
Егер топта
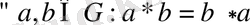 шарты орындалса, онда топ
абельдік (немесе коммутативті) топ
деп аталады.
шарты орындалса, онда топ
абельдік (немесе коммутативті) топ
деп аталады.
Анықтама 14.
R жиынында
 және
және
 операциялары бинарлық операция болып ж»әне келесі шарттар орындалса:
операциялары бинарлық операция болып ж»әне келесі шарттар орындалса:
- R -операциясына қатысты абельдік топ
- - операциясы ассоциативті, яғни
- Дистрибутивтілік заңы орындалса, яғни
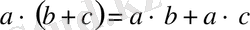 және
және
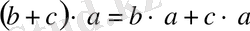
онда R жиыны
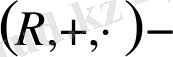 сақина
деп аталады.
сақина
деп аталады.
Анықтама 15.
- Сақинабірлік элементті сақинадеп аталады, егер сақинада мультипликативті бірлік элемент бар болса, яғни, .
- Сақинакоммутативті сақинадеп аталады, егероперациясы коммутативі болса.
- Сақина бүтін сақина деп аталады, егер сақина коммутативті, бірлік элементті сақинаболса, болғанданемесе.
- Сақинаденедеп аталады, егержәне R-ден басқа қатысты топ құрайтын болса.
Анықтама 16. Коммутативті дене өріс деп аталады.
Мысал.
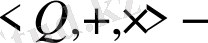 өріс
өріс
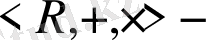 өріс
өріс
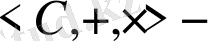 өріс
өріс
Анықтама 17. Топ ақырлы (ақырсыз) топ деп аталады, егер ақырлы (ақырсыз) сан элементтерінен тұратын болса. Ақырлы топтың элементтер саны оның реті деп аталады.
Анықтама 18.
p
жай саны үшін
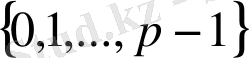 бүтін сандар жиынын
арқылы белгілейік және
бүтін сандар жиынын
арқылы белгілейік және
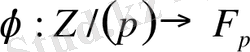 бейнелеуі келесі шартпен анықталсын
a
=0, 1, …,
p
-1 үшін
бейнелеуі келесі шартпен анықталсын
a
=0, 1, …,
p
-1 үшін
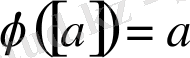 . Онда
. Онда
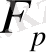 жиыны өріс құрылымы
жиыны өріс құрылымы
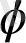 индуцияланған бейнесімен
p
-
ретті Галуа өрісі
деп аталады (көп жағдайда
GF
(
p
) символымен белгіленеді) .
индуцияланған бейнесімен
p
-
ретті Галуа өрісі
деп аталады (көп жағдайда
GF
(
p
) символымен белгіленеді) .
Анықтама 19.
K - өріс болсын. Ал,
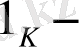 бірлік элементі. Егер
бірлік элементі. Егер
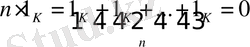
теңдігі орындалатындай (ең кіші)
 саны табылса, мұндай сан
K өрісінің сипаттамасы
деп аталады. Белгіленуі:
саны табылса, мұндай сан
K өрісінің сипаттамасы
деп аталады. Белгіленуі:
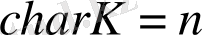 .
.
Егер n (
 ) саны табылмаса, онда K өрісінің сипаттамасы 0-ге тең.
) саны табылмаса, онда K өрісінің сипаттамасы 0-ге тең.
Анықтама 20.
Егер
 , P, K өріс болса, онда P өрісі K өрісінің
ішкі өрісі
деп аталады, ал K өрісі P өрісінің
кеңейтілімі
деп аталады.
, P, K өріс болса, онда P өрісі K өрісінің
ішкі өрісі
деп аталады, ал K өрісі P өрісінің
кеңейтілімі
деп аталады.
Анықтама 21.
P - өріс,
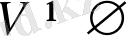 . V жиынында
. V жиынында
- анықталып және
Егер:
- абельдік топ болса;
шарттары орындалса, V жиыны P өрісіндегі векторлық кеңістік деп аталады.
Анықтама 22. V - векторлық кеңістік, P - өріс.
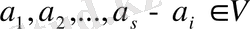 ақырлы жүйе (1)
ақырлы жүйе (1)
Егер
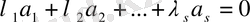 теңдігі орындалатындай кемінде
теңдігі орындалатындай кемінде
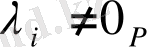 ,
,
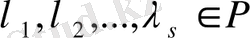 табылса, онда (1) жүйе
сызықтық тәуелді
деп аталады. Керісінше,
табылса, онда (1) жүйе
сызықтық тәуелді
деп аталады. Керісінше,
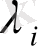 -дің барлығы 0-ге тең болғанда ғана орындалса, онда (1) жүйе
сызықтық тәуелді
деп аталады.
-дің барлығы 0-ге тең болғанда ғана орындалса, онда (1) жүйе
сызықтық тәуелді
деп аталады.
- q элементтен тұратын өріс
- n қатардан, k бағаннан тұратын матрица
- транспонирленген А матрицасы
- [X] - X санының бүтін бөлігі
- ] X[ - Х санынан кіші емес ең үлкен бүтін сан
КІРІСПЕ
Қазіргі заманда дискретті математиканың түрлі салаларда қолданулары бар. Ақырлы өрістер теориясы қазіргі абстракт алгебраның негізгі бөлімінің бірі болып табылады. Ақырлы өрістердің қолдануларының негізгі салаларының бірі - кодтау теориясы. Кодтау теориясының пәні берілген ақпараттың нақтылығын қамтамасыз ету болып табылады. Кодтау теориясы өзінің бастауын Шеннонның кодтау туралы танымал теоремасынан алады. Онда ақпаратты беруде кез-келген жылдамдықта қатенің аз болу ықтималдығында қолданылатын кодтар табылады деп дәлелденген.
Ақпаратты жіберу теориясының маңызды мәселелерінің ішінде - ақпаратты шулы арна бойынша сенімді түрде жіберу мақсатында оны кодтау және кодсыздандыру. Ақпаратты жіберу теориясында әдетте элементтері ақырлы алфавиттен алынған ақырлы тізбекті символдардан тұратын хабарламаны жіберу керек. Мысалы, бұл алфавит 0 және 1 символдарынан тұрсын, онда бұл хабарламаны екілік жүйеде жазылған сан ретінде қарастырамыз. Жалпы жағдайда, осы ақырлы алфавитіміз ақырлы өріс болып табылады.
Кодтау теориясының негізгі мәселесі - байланыс арнасының шуы нәтижесінде пайда болатын қателер ықтималдығының ең аз болуында. Хабарлама жіберудің сенімділігін арттыру әдістері ақырлы өрістердің қасиеттеріне негізделеді.
Диссертация ақырлы өрістер теориясының негіздерін алгебралық кодтау теориясына қолдану мәселелеріне арналған. Алгебралық кодтау теориясының басты мақсаты - қателікті түзетуші кодтар мен қателікті айқындаушы кодтарды құру әдістерін зерттеу. Жұмыста бинарлық сызықтық кодтардың бір түрі - Хэмминг коды зерттеледі, Хэмминг кодын құру алгоритмі қарастырылады.
Жұмыстың бірінші бөлімінде тақырыпты талдауға қажетті негізгі алгебралық түсініктер мен мағлұматтар, ақырлы өрістер теориясының кодтау теориясына қолданулары, кодтардың түрлері, арналарға жіберілетін сөздерді кодтау және кодсыздандыру әдістері қарастырылады.
Диссертацияның екінші бөлімінде бинарлық сызықтық кодтардың бір түрі - Хэмминг коды зерттеледі; Хэмминг кодын құру алгоритмдері және осы кодты кодсыздандыру әдістері қарастырылады, сонымен қатар Хэмминг кодының мысалына компьютерлік бағдарлама құрылды.
Үшінші бөлімде топтық, блокты, циклдік кодтар қарастырылады, сонымен қатар, хабарларды арналарға сенімді жіберудің ықтималдығы қарастырылады. Жұмыста алгебралық «Кодтау теориясының негіздері» тақырыбы бойынша орта мектеп оқушыларына арналған факультатив құрылды.
Жұмыстың мақсаты - ақырлы өрістер теориясының кодтау теориясында қолданылуы, қателерді табатын және түзететін кодтарды құру әдістерін зерттеу. Диссертация алгебралық кодтау теориясына арналған. Жұмыста сақиналар теориясы мен өрістер теориясының зерттеу әдістері қолданылады. Зерттеу нысаны - қателікті түзетуші кодтар мен қателікті айқындаушы кодтарды құру әдістері.
Зерттеу жұмысының нәтижесі 17-18 сәуірде Көкшетау қаласы, Ш. Уәлиханов атындағы Көкшетау мемлекеттік университетінде өткен Қазақтың ұлы ғалымы, тарихшы, этнограф, саяхатшы және ағартушы Ш. Уәлихановтың 180 жылдығына арналған «ШОҚАН ОҚУЛАРЫ - 19» Халықаралық ғылыми-тәжірибелік конференция материалдарында «Кодтау теориясының негіздері», «Хэмминг коды» деген тақырыпта жарық көрді. Зерттеу жұмысының нәтижесін жоғары оқу орындарында студенттерге «Дискретті математика» пәнін оқытуда қолдануға болады.
- АҚЫРЛЫ ӨРІСТЕР ТЕОРИЯСЫНЫҢ ҚОЛДАНУЛАРЫКодтау теориясы туралы жалпы ұғым
Кодтау теориясы - компьютингтің дамуына өз үлесін қосқан математиканың бір облысы болып табылады. Оның таралу облысы мәліметтерді нақты каналдар бойынша беру, ал оның пәні берілген ақпараттың нақтылығын қамтамасыз ету болып табылады. Кейбірде кодтау теориясын шифрлеумен шатастырады, бірақ ол дұрыс емес: криптография кері есепті шешеді, оның мақсаты - мәліметтерден ақпаратты алуды қиындату. Кодтау теориясы - мәліметтерді жоғалтпай алуды қамтамасыз етеді. Мәліметтерді кодтаудың қажеттілігімен алғашқы рет жүз елу жыл бұрын тап болды. Каналдар өте қымбат және сенімсіз болғандықтан телеграммаларды жіберудің өте тиімді жолдары қарастырылды. 1845 жылы пайдалануға арнайы кодтау кітаптары шықты; олардың көмегімен телеграфистер қолмен мәліметтердегі ұзақ сөйлемдерді қысқа кодтармен алмастырды. Сол кездері мәліметтердің жіберілуінің дұрыстығын тексеру үшін жұптық бақылау әдісі қолданылды, бұл әдісті перфокарталардың дұрыстығын тексеру үшін компьютердің бірінші және екінші буындарында да қолданылды. Ол үшін ең соңғы мәліметтер колодасына арнайы дайындалған бақылау сомасы бар картаны салған. Егер енгізу құрылғысы сенімсіз болса (немесе колода тым ұзын болған жағдайда), онда қате тууы мүмкін. Оны жөндеу үшін картадағы сомамен сәйкес келмегенше процедураны қайталай беретін. Бұл сұлбаның ыңғайсыз болғанымен қатар, ол екі есе қателер жіберетін. Байланыс каналдарының дамуымен қатар бақылаудың өте тиімді механизмі керек болды. Бұл мәселенің теориялық шешімін алғашқы болып ақпараттың статистикалық теориясының негізін қалаушы Клод Шеннон ұсынды. Шеннон өз заманының жұлдызы болды, ол АҚШ-тың академиялық элитасының мүшесі болған. Ванневар Буштың аспиранты болып, ол 1940 жылы жасы 30 жетпеген оқымыстыларға берілетін Нобель атындағы сыйлыққа ие болды. Bell Labs жұмыс істеп жүріп Шеннон «Мәліметтерді жіберудің математикалық теориясы» (1948) атты жұмыс жазды, ол жұмыста Шеннон каналдың жіберу мүмкіндігі мәліметтердің энтропия бастауынан жоғары болса, онда мәліметтерді ешқандай ақаусыз жіберілетіндей етіп кодтап қоюға болатынын дәлелдеді. Бұл түйіндеме Шеннонның көптеген дәлелдеген теоремалардың біреуінде бар. Сонымен қатар, ол каналда шудың бар болуына қарамастан мәліметтің жіберілу мүмкіндігінің теориялы түрде дәлелдеп берді. Шеннонның Мичиган штатында өзінің туып өскен қаласында орнатылған ескерткішінде ойып жазылған формуланы
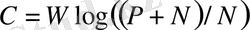 Альберт Эйнштейннің
Альберт Эйнштейннің
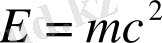 формуласының мәнімен салыстырады. Шеннонның еңбектері ақпараттар теория облысындағы әрі қарай зерттеулерінде өз ықпалын тигізді, бірақ оларда инженерлік практикалық қосымшасы болмады. Теориядан практикаға алмасу Ричарда Хэммингтің жұмысына байланысты болды. Ол Шеннонның Bell Labs бойынша әріптесі болды және кодтар класын ашқандығы үшін әйгілі болды, оларды «Хэмминг коды» деп атады. Өзінің жаңалығын Хемминг 40 жылдардың ортасында Bell Model V есептеуіш машинасының перфокарталармен жұмыс жасау қолайсыздығынан ашты деген аңыз бар. Оған операторлар жоқ болғанда, яғни демалыс күндерде машинамен жұмыс жасауға мүмкіндік берді және ол өзі енгізулермен жұмыс жасады. Хемминг байланыс каналдарындағы, сонымен қатар компьютерлердегі ақпараттарды беру магистральдарында, ең бастысы жад пен процессор арасындағы қателерді түзете алатын кодты ұсынды. Хемминг коды Шеннон теоремасында көрсетілген мүмкіндіктерді практикалық түрде қалай іске асыруға болатындығын көрсетеді. Хемминг өзінің мақаласын 1950 жылы жарыққа шығарды
,
бірақ ішкі жазбаларда кодтау теориясы 1947 жылмен белгіленген. Сондықтан кейбіреулер кодтау теориясының атасы ретінде Шеннонды емес, Хеммингті атау керек деп ойлайды. Хемминг бірінші болып «қателерді түзейтін кодтарды» (Error-Correcting Code, ECC) ұсынғандығы анық екенін білеміз. Бұл кодтардың қазіргі заманғы модификациялары барлық ақпараттарды сақтау жүйелерінде және жад пен процессор арасындағы алмасулар үшін қолданатыны белгілі. Олардың бір нұсқасы Рид-Соломонның коды компакт-дискілерде қолданылады. Хэмминг тәсілі бойынша жасалынған көптеген кодтар нұсқалары бар, олар кодтау алгоритмдері бойынша және тексеретін биттер саны бойынша айырмашылықтары бар. Мұндай кодтарға планетааралық станциялармен космостық байланыс жасау үшін ерекше көңіл беріле бастады, мысалы, Рид-Мюллердің кодтарын 7 ақпараттық битке 32 тексеруші бит немесе 6 ақпараттық битқа 26 тексеруші биттар келетін болды.
формуласының мәнімен салыстырады. Шеннонның еңбектері ақпараттар теория облысындағы әрі қарай зерттеулерінде өз ықпалын тигізді, бірақ оларда инженерлік практикалық қосымшасы болмады. Теориядан практикаға алмасу Ричарда Хэммингтің жұмысына байланысты болды. Ол Шеннонның Bell Labs бойынша әріптесі болды және кодтар класын ашқандығы үшін әйгілі болды, оларды «Хэмминг коды» деп атады. Өзінің жаңалығын Хемминг 40 жылдардың ортасында Bell Model V есептеуіш машинасының перфокарталармен жұмыс жасау қолайсыздығынан ашты деген аңыз бар. Оған операторлар жоқ болғанда, яғни демалыс күндерде машинамен жұмыс жасауға мүмкіндік берді және ол өзі енгізулермен жұмыс жасады. Хемминг байланыс каналдарындағы, сонымен қатар компьютерлердегі ақпараттарды беру магистральдарында, ең бастысы жад пен процессор арасындағы қателерді түзете алатын кодты ұсынды. Хемминг коды Шеннон теоремасында көрсетілген мүмкіндіктерді практикалық түрде қалай іске асыруға болатындығын көрсетеді. Хемминг өзінің мақаласын 1950 жылы жарыққа шығарды
,
бірақ ішкі жазбаларда кодтау теориясы 1947 жылмен белгіленген. Сондықтан кейбіреулер кодтау теориясының атасы ретінде Шеннонды емес, Хеммингті атау керек деп ойлайды. Хемминг бірінші болып «қателерді түзейтін кодтарды» (Error-Correcting Code, ECC) ұсынғандығы анық екенін білеміз. Бұл кодтардың қазіргі заманғы модификациялары барлық ақпараттарды сақтау жүйелерінде және жад пен процессор арасындағы алмасулар үшін қолданатыны белгілі. Олардың бір нұсқасы Рид-Соломонның коды компакт-дискілерде қолданылады. Хэмминг тәсілі бойынша жасалынған көптеген кодтар нұсқалары бар, олар кодтау алгоритмдері бойынша және тексеретін биттер саны бойынша айырмашылықтары бар. Мұндай кодтарға планетааралық станциялармен космостық байланыс жасау үшін ерекше көңіл беріле бастады, мысалы, Рид-Мюллердің кодтарын 7 ақпараттық битке 32 тексеруші бит немесе 6 ақпараттық битқа 26 тексеруші биттар келетін болды.
ECC жаңа кодтардың бірі ретінде LDPC (Low-Density Parity-check Code) кодын айтуымызға болады. Негізінде олар отыз жыл бұрын танымал болған, бірақ қазіргі уақытта оларға ерекше көңіл бөлінуде. LDPC коды 100 пайыздық анықтылығы болмағанмен, ол қатенің мүмкіндігін керекті нәтижеге дейін жеткізуімізге мүмкіндік береді және сонымен қатар каналдың жіберу мүмкіндігі максимальді толық түрде қолданылады. Оларға «турбокодтар» (Turbo Code) өте жақын келеді, олар алыс космостағы объектілермен жұмыс жасағанда өте қолайлы. Кодтау теориясының тарихына Владимир Александрович Котельниковтың аты нық жазылған. 1933 жылғы «Материалах по радиосвязи к I Всесоюзному съезду по вопросам технической реконструкции связи»-да ол өзінің «О пропускной способности «эфира» и «проволоки» атты жұмысын жариялады. Бұл теоремада жіберілген сигнал ақпараттың жоғалтуынсыз қайтадан қалпына келетін шарттарды анықтайды.
Бұл теореманы әркім әрқалай атайды, соның ішінде «WKS теоремасы» (Whittaker, Kotelnikov, Shannon) . Кейбір бастауларда Nyquist-Shannon sampling theorem және Whittaker-Shannon sampling theorem деп те аталады, ал өзіміздің жоғарғы оқу орындарының оқулықтарында жай ғана «Котельников теоремасы» деп кездестіреміз.
Бүгінгі күнде ақпараттарды арналарға сенімді түрде жіберу, соның ішінде ақпараттарды кодтау және кодсыздандыру арқылы жіберу үлкен мәселеге айналып отыр. Әдетте, элементтері ақырлы алфавиттен алынған ақырлы тізбекті символдардан тұратын хабарламаны жіберу керек болады. Мысалы, бұл алфавит 0 және 1 символдарынан тұрсын, онда бұл хабарламаны екі сан ретінде қарастырамыз. Жалпы жағдайда, осы ақырлы алфавитіміз ақырлы өріс болып табылады.
Кодтау теориясының негізгі есебінің нәтижесі байланыс арналарының шуының қате ықтималдығының ең аз болуында. Хабарлама жіберудің сенімділігін арттыру әдісі негізінен ақырлы өрістердің қасиеттеріне байланысты.
Алгебралық кодтау теориясының негізгі идеясы хабарламаны артық ақпаратпен бірге жіберу. Бұл хабарламаны құрайтын тізбек символдарының кез-келген арнайы бейнесі тізбектің ұзындығымен бейнеленетінін көрсетеді.
1-суретте байланыс жүйесінің қарапайым моделі көрсетілген [1, 588 б. ] .
«шу»
Байланыс
каналы
1-сурет
Біз жіберген және кодсыздандырылған хабарламаны құрайтын символдар бір ғана
ақырлы өрісінің элементтері болатынын байқаймыз. Яғни, кодтау дегеніміз,
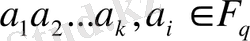 k
символдық блоктан тұратын жіберілген хабарламаны ұзындығы
n
>
k
болатын
k
символдық блоктан тұратын жіберілген хабарламаны ұзындығы
n
>
k
болатын
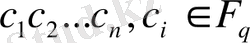 кодтаушы сөздерімен алмастырады. Біз кодталған сөздерді
n
өлшемді
кодтаушы сөздерімен алмастырады. Біз кодталған сөздерді
n
өлшемді
 жол-вектор ретінде қарастырамыз. 1-суреттегі
f:
жол-вектор ретінде қарастырамыз. 1-суреттегі
f:
 бейнелейтін функция
кодтау схемасы
деп, ал
g:
бейнелейтін функция
кодтау схемасы
деп, ал
g:
 кодсыздандыру схемасы
деп аталады.
кодсыздандыру схемасы
деп аталады.
- Сызықтық кодтар
Анықтама 1. 2. 1.
 өрісінен алынған
өрісінен алынған
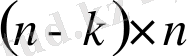 өлшемді және рангісі
өлшемді және рангісі
 болатын матрица болсын.
С
-
болатын матрица болсын.
С
-
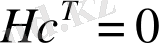 шартын қанағаттандыратын
шартын қанағаттандыратын
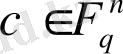 n
-өлшемді векторлар жиыны. С жиыны
n
-өлшемді векторлар жиыны. С жиыны
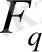 өрісінде
өрісінде
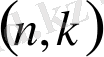 -
сызықтық код
деп аталады
.
-
сызықтық код
деп аталады
.
 Мұндағы,
n -
кодтың ұзындығы
, ал
k -
кодтың өлшемі
деп аталады.
С
жиынының элементтері
кодталған сөздер
(немесе
кодталған векторлар
), ал,
Н
матрицасы
С
жиынының
тексеруші кодтау матрицасы
деп аталады. Егер
q=2
болса, С -
бинарлық код
деп аталады. Егер H матрицасының түрі
Мұндағы,
n -
кодтың ұзындығы
, ал
k -
кодтың өлшемі
деп аталады.
С
жиынының элементтері
кодталған сөздер
(немесе
кодталған векторлар
), ал,
Н
матрицасы
С
жиынының
тексеруші кодтау матрицасы
деп аталады. Егер
q=2
болса, С -
бинарлық код
деп аталады. Егер H матрицасының түрі
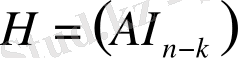 болса, онда
С
-
жүйелік код
деп аталады. Ескерту. С жиыны
болса, онда
С
-
жүйелік код
деп аталады. Ескерту. С жиыны
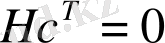 сызықтық теңдеулер жүйесінің шешімі болса,
сызықтық теңдеулер жүйесінің шешімі болса,
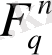 векторлық кеңістігінің
k
өлшемді ішкі кеңістігі болады және кодталған сөздер қосу операциясына қатысты топ құрап,
С
топтық код
деп аталады.
векторлық кеңістігінің
k
өлшемді ішкі кеңістігі болады және кодталған сөздер қосу операциясына қатысты топ құрап,
С
топтық код
деп аталады.
Мысал 1. 2. 2.
H - өлшемі
 болатын
болатын
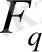 өрісінен алынған матрица болсын:
өрісінен алынған матрица болсын:

H
=
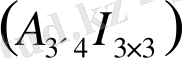 :
:
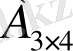 =
=
 ,
,
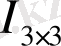 =
=
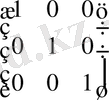
Тексеруші символдарды
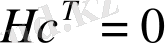 теңдеулер жүйесінен табуға болады.
теңдеулер жүйесінен табуға болады.
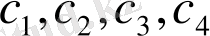 төмендегідей берілген деп есептейік:
төмендегідей берілген деп есептейік:
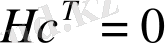
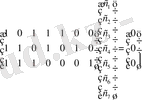
Сонда мынадай жүйе шығады:
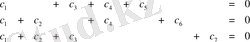
Онда бізде өрісіміз
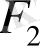 болғандықтан
болғандықтан
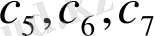 тексеруші символдарын келесідей беруге болады.
тексеруші символдарын келесідей беруге болады.
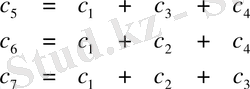
Ендеше, бұл жағдайда кодтау схемасы


бейнелейтін сызықты бейнелеу болады.
Кодтаудың мысалдары:
а) Е - кодтауы натурал сандардың екілік жазылуы. n=0 санына
 сөзі сәйкес қойылады, ал
сөзі сәйкес қойылады, ал
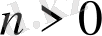 санына
санына
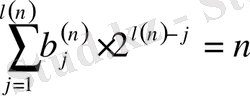
шартын қанағаттандыратын ұзындығы ең қысқа
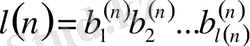
сөзін сәйкес қоямыз.
Әрине, n - санының жазылуы 1 цифрынан басталады, яғни
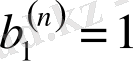 , ал таңбалар саны -
, ал таңбалар саны -
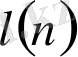 келесі екілік теңсіздікті қанағаттандыруы тиісті:
келесі екілік теңсіздікті қанағаттандыруы тиісті:
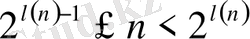
Сонымен,
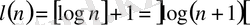 ,
мұндағы
,
мұндағы
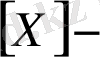 өрнегі Х - санының бүтін бөлігі, ал
өрнегі Х - санының бүтін бөлігі, ал
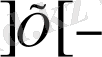 өрнегі Х санынан кіші емес ең кіші бүтін сан.
өрнегі Х санынан кіші емес ең кіші бүтін сан.
Е кодтауы өзара бірмәнді бейнелеу (сәйкестік) :
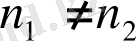 болғанда
болғанда
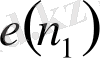 және
және
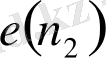 сөздері әртүрлі.
сөздері әртүрлі.
б)
 алғашқы
алғашқы
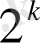 натурал санды кодтау. Әрбір
n
натурал санына
натурал санды кодтау. Әрбір
n
натурал санына
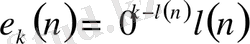 сөзін сәйкес қояды.
сөзін сәйкес қояды.
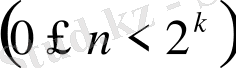 .
.
 сөзі
n
санының
k
-цифрдың көмегімен екілік жазылуы деп аталады.
сөзі
n
санының
k
-цифрдың көмегімен екілік жазылуы деп аталады.
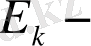 кодтауында алғашқы
кодтауында алғашқы
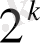 натурал сан ұзындығы k болатын екілік сөздер жиынына бейнеленеді. 1-кестеде Е және
натурал сан ұзындығы k болатын екілік сөздер жиынына бейнеленеді. 1-кестеде Е және
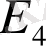 кодтауларындағы 0-ден 15-ке дейінгі сандарға сәйкес келетін сөздер келтірілген [2, 300 б. ] .
кодтауларындағы 0-ден 15-ке дейінгі сандарға сәйкес келетін сөздер келтірілген [2, 300 б. ] .
Кесте 1
Е және E 4 кодтауларындағы 0-ден 15-ке дейінгі сандарға сәйкес келетін сөздер
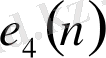
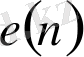
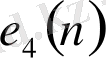
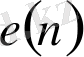
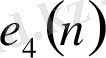
в) Пошта индексіндегі цифрларды жазудағы қолданылатын кодтау.
Хат жолдаушының қалыптағы тоғыз кесіндісінің көмегімен жазған әрбір ондық цифры автоматты түрде танылуы үшін ол В алфавитінде ұзындығы тоғызға тең сөзбен кодталады.
1 таңбасына қолданылатын кесінділердің нөмірлері 3, 4, 8 сандарына сәйкес келеді.
Мысалы, 2 цифрына 1, 4, 7, 9 нөмірлері сәйкес келсе, оған 100100101 сөзі сәйкес келеді. 5 цифрына 110010011 сөзі сәйкес келеді.
Ақырлы жиындарды екілік сөздердің кейбір ішкі жиынына бейнелеуді осы жиындардың элементтерінің санын есептеу немесе бағалау арқылы беру өте қолайлы.
Мысалы n санының теріс емес бүтін m қосылғышқа ретті жіктелуі (үлестірілуі) болатын
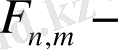 жиынын қарастырайық.
жиынын қарастырайық.
Әрбір
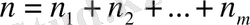 жіктелуіне
жіктелуіне
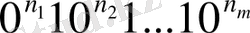 сөзін сәйкес қоямыз. Бұл сөздің ұзындығы
сөзін сәйкес қоямыз. Бұл сөздің ұзындығы
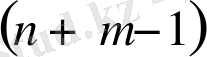 , яғни, ол n- нөлдерден және
, яғни, ол n- нөлдерден және
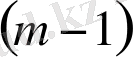 бірлерден тұрады. Бірлер нөлдердің тізбектерін бір-бірінен ажырату үшін қажет.
бірлерден тұрады. Бірлер нөлдердің тізбектерін бір-бірінен ажырату үшін қажет.
11 санының 4 қосылғышқа жіктелуін қарастырайық 11=5+0+2+4 болса, оған сәйкес келетін кодтық сөз 11001. 11=2+7+2+0 болса, онда ол 00110011 сөзімен, ал 11=1+1+6+3 болса, 01011000 сөзімен кодталады. Мұндай кодтау
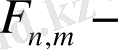 жиынын ұзындығы
жиынын ұзындығы
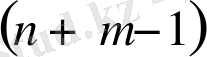 болатын еселік сөздер жиынына өзара бірмәнді бейнелеу болады. Мұндағы әрбір
болатын еселік сөздер жиынына өзара бірмәнді бейнелеу болады. Мұндағы әрбір
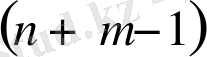 сөзде тура
сөзде тура
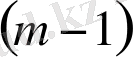 бірлер бар.
бірлер бар.
Мысал 1. 2. 3.
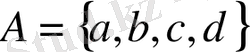 алфавиті және оның әріптерінің екілік кодтаулары берілсін:
алфавиті және оның әріптерінің екілік кодтаулары берілсін:
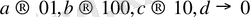
0100 сөзін db немесе add деп декодтауға болады, 0010100 сөзін ddcdd немесе daadd немесе dadb деп декодтауға болады.
Сонымен, көрсетілген натурал сандарды әріптері бойынша кодтау өзара бірмәнді сәйкестік болмайды. Егер алфавиттің барлық әріптерінің кодтарының ұзындықтары бірдей болса, онда код бірқалыпты деп аталады.
Мысал 1. 2. 4.
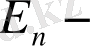 коды бірқалыпты.
коды бірқалыпты.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz