Сызықтық дифференциалдық теңдеу

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. Әуезов атындағы Оңтүстік Қазақстан Университеті

ӘОЖ-514(023 ) қолжазба құқығында

Маханова Кулаш Жакслыковна

Болашақ математика мұғалімдерін ақпараттық технологияларды пайдалану негізінде дифференциалдық теңдеулерді шешуге оқыту әдістемесі

7M01510 - «Математика» білім беру бағдарламасы бойынша

педагогика ғылымдарының магистрі дәрежесін алу үшін

дайындалған диссертация

Ғылыми жетекшісі:

Шымкент 2023

КІРІСПЕ

Қоғам дамуының қазіргі кезеңінде адам қызметінің барлық салалары ақпараттандырылуда. Осылайша, қазіргі қоғам және оның үнемі дамып келе жатқан экономикасы жаңа ақпараттық технологияларды сауатты қолдана алатын қызметтің барлық салаларында мақсатты және бастамашыл жоғары білікті мамандарға мұқтаж.

Білім беруді ақпараттандыру туралы алғаш рет 1990 жылдарда "Информатика және білім беру" журналында жарияланған. Сонымен бірге, 1990 жылдан бері жарияланған басылымдарға қарамастан, бұл мәселе және қазіргі уақытта ол соңына дейін шешілмеген.

Білім беруде ақпараттық технологияларды қолдану әдістемесі В. Л. В. П. Андреев, Б. С. Беспалько, А. П. Гершунский, И. Г. Ершов, В. Г. Захарова, И. Л. Кинелев, Б. И. Лернер, В. М. Машбиц, П. И. Монахов, Ю. А. Образцов, Е. С. Первин, Г. К. Полат және т. б. көптеген еңбектерінде зерттелген. Бұлар арқылы ақпараттық технологияларды қолданудың нақты жолдары әзірленуде, оқытуда бұл технологияларды дидактикалық құрал ретінде пайдалану, психологиялық педагогикалық зерттеулер жүргізу кезінде оқытудың әртүрлі нысандарын іске асыру үшін оқытуды автоматтандыру, автоматтандырылған оқыту жүйелерін қолдана отырып оқытуды автоматтандыру, сценарийді әзірлеуді, сараптаманы және т. б. қоса алғанда, компьютерлік оқу курстарын және грамматикалық-әдістемелік кешендерді, педагогикалық бағдарламалық құралдардың сапасын бағалау және т. б.

Болашақ математика мұғалімінің дайындық мәселелерін зерттейтін көптеген жұмыстар бар, оларға И. И. Баврин, Д. А. Власов, Г. Д. Глейзер, В. А. Горелик, В. А. Гусева, О. Б. Епишева, А. Ж. Жафярова, О. А. Иванова, В. И. Игошина, Ю. М. Колягина, Э. И. Кузнецова, В. Ф. Люби чева, В. Л. Матросова, В. М. Монахова, А. И. Нижникова, г. И. Саранцева, Н. Л. және т. б. жоғары оқу орындарында дифференциалдық теңдеулерді шешуді оқытуда өзінің кәсіби және қолданбалы дамуын табады.

Алайда, бұл жұмыстар мемлекеттік жаңа буын кәсіптік білім беру стандарттарына көшуге байланысты аспектілерді жеткілікті түрде көрсетпейді. Атап айтқанда, математикалық пәндерді оқу кезінде математика мұғалімін кәсіби даярлауда ақпараттық технологияларды қолдану туралы мәселелер қамтылмаған.

Дифференциалдық теңдеулер курсына қатысты зерттеулердің көпшілігі математиканың осы бөлімінің қолданбалы бағыты бойынша келіседі. Сонымен қатар ақпараттық технологиялар арқылы осы бағытты іске асыру бойынша жұмыстар жоқтың қасы.

Осылайша, болашақ математика мұғалімдерінің математикалық дайындығына байланысты бірқатар қайшылықтар бар. Олардың ішінде мыналарды бөліп көрсетуге болады:

* еліміздің білім беру стандартына сәйкес университеттің білім беру процесін құру қажеттілігі арасында, болашақ пән мұғалімдерінде ақпараттық технологияларды қолдану қабілетін қалыптастыруға және ғылыми әдістемелік әдебиеттер мен заманауи зерттеулерде осы мәселелердің жеткіліксіз дамуына ықпал ететін математикалық курстарды әдістемелік қамтамасыз етуді құруды көздейді;

* Ақпараттық технологиялар құралдарының, атап айтқанда, әртүрлі шешімдерді шешуге үлкен мүмкіндіктері бар компьютерлік бағдарламалардың болуы, математикалық есептер, оның ішінде дифференциалды есептер, және оларды болашақ мұғалімдердің тақырыптық дайындығында қолдануға байланысты әзірлемелердің жеткіліксіздігі.

Көрсетілген қарама-қайшылықтар осы зерттеудің тақырыбын таңдауды анықтайды.

Зерттеу мәселесі жоғарыда айтылған қарама-қайшылықтан және педагогикалық жоғары оқу орнында болашақ математика мұғалімдерін ақпараттық технологияны пайдалану негізінде дифференциалдық теңдеулерді шешу әдістемесін жасаудан туындайды.

Зерттеу объектісі : жоғары педагогикалық білім беруде математика пәні мұғалімін дайындау үдерісі.

Зерттеу пәні: болашақ математика пәні мұғалімдерін ақпараттық технологияларды пайдалану негізінде дифференциялық теңдеулерді шешуге оқыту.

Зерттеудің мақсаты- дифференциалдық теңдеулер курсының қолданбалы мәнін түсінетін және дифференциалдық теңдеулерді шешу үшін жаңа ақпараттық технологиялар құралдарын қолдана алатын білікті математика мұғалімдерін даярлауға мүмкіндік беретін білім беруді ақпараттандыру жағдайында дифференциалдық теңдеулерді шешуді оқыту әдістемесін әзірлеу.

Зерттеу гипотезасы: ақпараттық технологияларды, атап айтқанда компьютерлік бағдарламаларды қолдана отырып, дифференциалдық теңдеулерді шешуге үйрету болашақ математика мұғалімдерінің математикалық дайындығының сапасын арттыруға ықпал етеді және дәстүрлі әдістерді, формалар мен құралдарды дифференциалдық теңдеулерді шешу әдістерімен оңтайлы үйлестіретін дифференциалдық теңдеулерді шешуді оқыту әдістемесін әзірлеу арқылы іске асырылған компьютерлік бағдарламалар курстың қолданбалы бағытын күшейтуге мүмкіндік береді,

Зерттеудің мақсатына, объектісіне, тақырыбына және гипотезасына сәйкес зерттеудің келесі міндеттері қойылды:

*"білім берудегі ақпараттық технологиялар" ұғымын талдау және болашақ математика мұғалімін дайындауда ақпараттық технологиялар құралы ретінде компьютерлік бағдарламаларды қолдану мүмкіндіктерін анықтау

* дифференциалдық теңдеулер курсы бойынша есептердің белгілі бір класын шешу үшін компьютерлік бағдарламаларды қолданудың орындылығын анықтау және негіздеу,

*дифференциалдық теңдеулерді шешуге арналған компьютерлік бағдарламалардың мүмкіндіктерін талдау және ең қолайлы бағдарламаларды таңдау;

• компьютерлік бағдарламаларды қолдана отырып, дифференциалдық теңдеулерді шешуді оқытудың моделін және оған сәйкес әдістемесін әзірлеу, оқытудың тиісті мақсаттарын, мазмұнын, әдістерін, нысандары мен құралдарын анықтау.

* ұсынылған оқыту әдістемесін қолданудың тиімділігін эксперименталды түрде тексеру.

Зерттеудің теориялық және әдістемелік негіздемесі: педагогикалық жоғары оқу орнында болашақ математика пәні мұғалімдерін кәсіби дайындық облысында (А. В. Абрамов, Р. М. Асланов, И. И. Баврин, В. А. Гусев, В. И. Игошин, Э. И. Кузнецов, С. И. Калинин, Н. Д. Кучугурова, Г. Л. Луканкин, В. Л. Матросов, А. Г. Мордкович, В. Р. Майер, А. И. Нижников, Л. В. Павлова, Е. И. Смирнов, И. Л. Тимофеева, Г. Г. Хамов, М. И. Шабунин, Л. В. Шкерина и др. ) ; білім беруді ақпараттандыру теориясында (Ю. С. Брановский, А. П. Ершов, С. А. Жданов, Т. Б. Захарова, С. Д. Каракозов, О. А. Козлов, Г. А. Кручинина, А. А. Кузнецов, Д. Ш. Матрос, Е. И. Машбиц, П. И. Образцов, Е. С. Полат, И. В. Роберт, Г. К. Селевко, Н. В. Софронова и др. ) ; математика сабағында ақпараттық және телекоммуникациялық технологияларды пайдаланудың әдістемелік аспектілерін (В. В. Алейников, И. В. Беленкова, Д. П. Голоскоков, И. Б, Горбунова, Е. А. Дахер, В. П. Дьяконов, С. А. Дьяченко, Е. В. Клименко, Т. Г. Кузьмичева, С. В. Поршнев, С. Е. Савотченко и др. ) зерттеу.

Қойылған міндеттерді шешу үшін мынадай зерттеу әдістері пайдаланылды: зерттеу мәселесі бойынша математикалық, психологиялық-педагогикалық, оқу және ғылыми-әдістемелік әдебиеттерді талдау; жоғары мектеп оқытушыларының педагогикалық тәжірибесін талдау және жалпылау; оқу процесінің барысын бақылау; педагогикалық университеттердің математика факультеттерінің студенттерімен, оқытушыларымен, түлектерімен әңгімелесу; студенттерге сауалнама жүргізу; педагогикалық эксперименттің анықтау, іздеу және оқыту кезеңдері; педагогикалық эксперименттің нәтижелерін өңдеу және түсіндіру.

Зерттеудің ғылыми жаңалығы:

* компьютерлік бағдарламаларды (Dfield, Pplane, Odesolve) қолдана отырып, дифференциалдық теңдеулерді шешуді оқытудың моделі мен оған сәйкес әдістемесі әзірленді және ұсынылды

* компьютерлік бағдарламаларды қолдана отырып, оқыту мен оқытудың дәстүрлі формасын оған сәйкес оқытудың негізгі формаларының бірі зертханалық-практикалық сабақты үйлестіру мүмкіндіктері ашылды

*қолданыстағы тапсырмалар іріктеліп алынды және жаңа компьютерлік-бағдарланған міндеттер, оның ішінде қолданбалы тапсырмалар әзірленді;

*компьютерлік бағдарламаларды дифференциалдық теңдеулер курсында көрнекілік құралдарының бірі ретінде пайдалану мүмкіндіктері көрсетілді.

Теориялық маңыздылығы: дифференциалдық теңдеулерді шешу үшін компьютерлік бағдарламаларды қолдану әдістемесі теориялық тұрғыдан негізделген және осы әдістеменің моделі ұсынылған. Dfield, Plane, Odesolve компьютерлік бағдарламалары дифференциалдық теңдеулерді шешуге үйретудегі жаңа ақпараттық технологиялардың құралы ретіндегі рөлі мен әлеуеті тұрғысынан егжей-тегжейлі зерттелген. Дифференциалдық теңдеулер курсында компьютерге бағытталған есептер бөлініп, оларды шешудің орындылығы негізделген.

Алынған нәтижелердің практикалық маңыздылығы, диссертацияда дифференциалдық теңдеулер курсына жаңа ақпараттық технологиялар құралдарын енгізу бойынша нақты ұсыныстар бар. Оқытудың бұл әдістемесі болашақ математика мұғалімдерінің кәсіби даярлығының сапасын арттыруға бағытталған педагогикалық жоғары оқу орындарының математикалық мамандықтарының студенттері үшін дифференциалдық теңдеулер бойынша бағдарламаларды, оқу құралдары мен оқулықтарды және оқу жоспарларын одан әрі жетілдіруге негіз бола алады.

1 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУ ҰҒЫМЫ

1. 1 Дифференциалдық теңдеулердің негізгі ұғымдары мен элементтері

Дифференциалдық теңдеу деп ізделінді функцияны, оның туындылары мен дифференциалдарын және аргументтерін байланыстыратын теңдеуді айтамыз.

Теңдеуге кіретін туындының (дифференциалдың) ең жоғарғы реті дифференциалдық теңдеудің реті деп аталады.

Дифференциалдық теңдеудің шешімі деп кез келген функцияны айтамыз, егер оның өзін, туындысын және дифференциалын теңдеуге қойғанда тепе-теңдік шығатын болса.

Тек қана бір айнымалыға (бірнеше айнымалыға) тәуелді дифференциалдық теңдеуді қарапайым (дербес туындылы) дифференциалдық теңдеулер деп айтамыз.

Айталғанға сай п - ші ретті жай дифференциалдық теңдеу жалпы түрде былай жазылады:

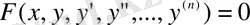(1. 1. 1)

Мұндағы х - тәуелсіз айнымалы, у - ізделінді функция, ал 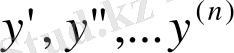-туындылар.

Егер (1. 1. 1) теңдеуде екі тәуелсіз айнымалыны 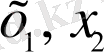бір ғана ізделінді функция 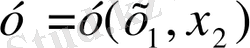болса, онда ол п - ші ретті дербес туындылы дифференциалдық теңдеу болар еді де, былай жазылар еді:

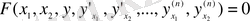
Егер (1. 1. 1) теңдеуде n=1 болса, онда алынған теңдеу

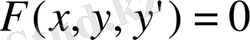(1. 1. 2)

бірінші ретті дифференциалдық теңдеу деп, ал қалған 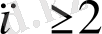болған жағдайларда жоғары ретті дифференциалдық теңдеу деп аталады.

Егер (1. 1. 2) теңдеу бойынша шешілетін болса, онда алынған теңдеу

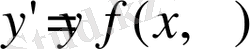(1. 1. 3)

туындысы бойынша шешілген бірінші ретті дифференциалдық теңдеу деп аталады. (1. 1. 3) теңдеудегі 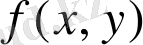функциясын кейінде берілген Д облысында бір мәнді, қос аргумент бойынша үздіксіз деп есептейміз. Д - облысы (1. 1. 3) теңдеудің анықталу облысы деп аталады.

Мысал 1.

а) 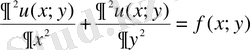- екінші ретті дербес туындылы дифференциалдық теңдеу;

б) 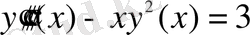- үшінші ретті қарапайым дифференциалдық теңдеу;

в) 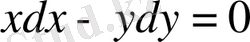- бірінші ретті қарапайым дифференциалдық теңдеу.

Ескерту 1. Ары қарай дифференциалдық теңдеу дегенді қарапайым дифференциалдық теңдеу деп түсінеміз. [1], [2] .

Мысал 2. Теңдеудің жалпы шешімін тап

а)

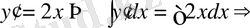
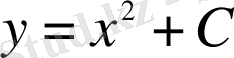(1. 1. 4)

(1. 1. 4) шешімі кез келген С тұрақтысына байланысты, яғни, С-ның әртүрлі мәнінде әртүрлі шешім аламыз. Енді С тұрақтысын анықтау үшін қосымша бір шарт (бастапқы шарт) берелік:

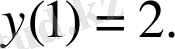
Онда осы бастапқы шартты (1) -ге қойсақ: 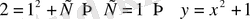- дербес шешім.

б)

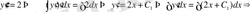
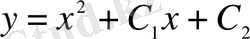- жалпы шешім. (1. 1. 5)

Екінші ретті (1. 1. 5) теңдеуі екі тұрақтыға байланысты С ₁ және С ₂ , оларды анықтау үшін екі шарт (бастапқы) қажет: 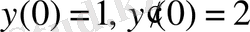. Бұдан:

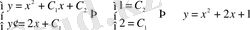- дербес шешім.

Геометриялық тұрғыдан, (1. 1. 4) және (1. 1. 5) шешімдері - параболалар жиынтығы. Бастапқы шарт берілді деген: осы параболалар жиынтығынан мына шарттарды қанағаттандыратын параболаны тап деген сөз:

а) 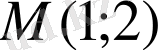нүктесі арқылы өтетін; б) 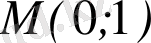нүктесі арқылы өтетін және 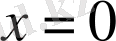нүктесінде жүргізілген жанамасының бұрыштық коэффиценті 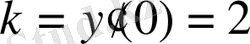болатын.

Коши теоремасы. Жалпы және дербес шешім

ші ретті айқын дифференциалдық теңдеу мына түрде жазылады:

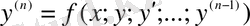, (1. 1. 6)

ал айқын емес ші ретті дифференциалдық теңдеу: .

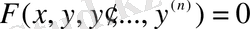Коши есебі. (1. 1. 3) дифференциалдық теңдеуінің, болғанда

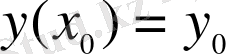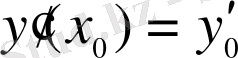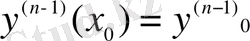, , …, (1. 1. 7)

бастапқы шартын қанағаттандыратын шешімдерін тап.

Коши теоремасы. Егер қандай да бір тұйық облыста 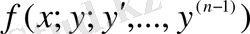функциясы барлық аргументі бойынша үзіліссіз болып және осы облыста оның дербес туындылары 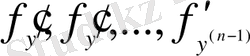табылса, онда (1. 1. 3) дифференциалдық теңдеуінің (1. 1. 4) бастапқы шартын қанағаттандыратын жалғыз шешімі болады, мұндағы 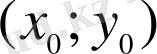нүктесі - осы облысқа тиісті нүкте. [2], [3] .

Кез келген дифференциалданатын функция

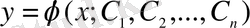, (1. 1. 8)

мұндағы 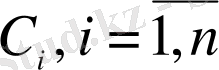- кез келген тұрақтылар, (1. 1. 5) дифференциалдық теңдеуінің жалпы шешімі деп аталады, егер:

а) ол 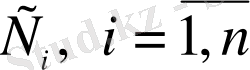-дің кез келген тұрақты мәндерінде (1. 1. 5) дифференциалдық теңдеуінің шешімі болса,

б) Коши теоремасының шартын қанағаттандыратын осы облыстың кез келген бастапқы шарты үшін,

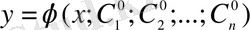(1. 1. 9)

шешімі бастапқы шартты қанағаттандыратындай 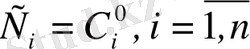тұрақтылары табылатын болса.

Дифференциал теңдеудің берілген облысындағы әрбір нүктесі үшін жалғыздық шарты орындалатын болса, онда (1. 1. 6) түріндегі шешім дербес шешім деп аталады.

Геометриялық тұрғыдан, (1. 1. 5) - қисықтар жиынтығы (интегралдық қисықтар) . Коши теоремасының шарты орындалды дегеніміз - облысқа тиісті кез келген 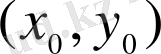нүктесінен (1. 1. 4) шартын қанағаттандыратын тек бір ғана қисық өтеді деген сөз.

(1. 1. 5) теңдеуінің айқын емес түрде берілген жалпы (дербес) шешімі:

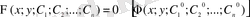сәйкесінше дифференциалдық теңдеудің жалпы (дербес) интегралы деп аталады. (1. 1. 5) теңдеуінің жалпы және дербес шешімінен басқа ерекше шешімдері болады.

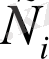-ді ( 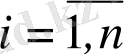) қандай етіп таңдап алсақ та, жалпы шешімнен шықпайтын және шешімнің жалғыздық шарты бұзылатын нүктелерде орналасқан (облыстың шекарасында) шешімдерді ерекше шешімдер деп атаймыз.

Мысал 3. Мынадай теңдеуді қарастыралық:

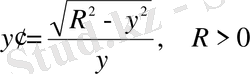(1. 1. 10)

Шешуі. Орнына қою арқылы (1. 1. 10) теңдеуінің жалпы интегралы:

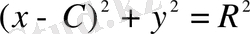(1. 1. 11)

болатынына көз жеткізуге болады.

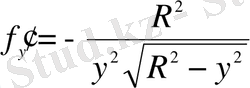, (1. 1. 12)

болғандықтан, 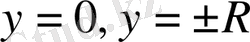түзулерінде 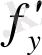- шектелмеген, яғни, Коши теоремасының шарты бұзылып тұр. (1. 1. 10) -теңдеуінің шешімі болмайтыны анық, ал 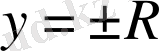түзулері (10) теңдеуінің шешімдері және бұл шешімдер жалпы шешім (11) -дегі қалай таңдалса да онымен беттеспейді, С=±∞ болса да. Геометриялық тұрғыдан, бұл - 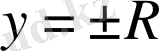түзулерінің кез келген нүктесі арқылы екі интегралдық қисық өтеді деген сөз. Мысалы, 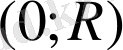нүктесі арқылы 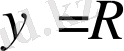және 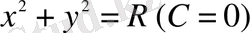қисықтары өтеді. Сонымен, 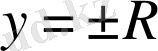- ерекше шешім.

2 мысалда байқағанымыздай, теңдеуді шешу кезінде біз алғашқы функция табамыз. Сондықтан, дифференциалдық теңдеудің шешімін табу процессі теңдеуді интегралдау деп аталады. [4], [5] .

1. 2 Сызықтық дифференциалдық теңдеу

Егер дифференциал теңдеу ізделінді функция мен оның туындысы бойынша сызықты болса, ондай теңдеуді сызықты дифференциал теңдеу деп атаймыз.

Бірінші ретті сызықты дифференциал теңдеуді мына түрде жазуға болады:

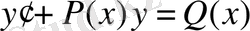(1. 1. 13)

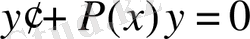, (1. 1. 14)

(1. 1. 13) - біртектес емес, ал (1. 1. 14) - біртектес дифференциал теңдеу деп аталады.

Біртектес дифференциал теңдеудің жалпы шешімін табалық:

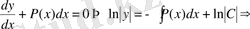
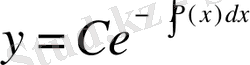(1. 1. 15)

Лагранж әдісін (тұрақты шаманы вариациалау әдісі) қолданып, (1. 1. 13) теңдеуінің шешімін алуға болады. Шешімді (1. 1. 15) түрінде іздейміз, мұндағы 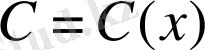- белгісіз функция. Онда (1. 1. 13) теңдеуіндегі -тың орнына:

,

ал - тің орнына (1. 1. 5) -ті қойсақ:

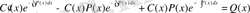
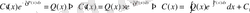
Осы табылған 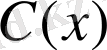-ті (1. 1. 5) -ке қоя отырып, (1. 1. 13) теңдеуінің жалпы шешімін аламыз.

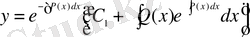(1. 1. 16)

Ескерту. 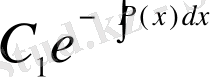- теңдеуінің жалпы шешімі, ал 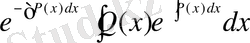- (1. 1. 13) теңдеуінің дербес шешімі ( болғанда) болғандықтан, кез келген ретті сызықтық теңдеу үшін ақиқат болатын мынадай тұжырым жасауға болады: біртектес емес сызықты теңдеудің жалпы шешімі оған сәйкес біртекті сызықтық теңдеудің жалпы шешімі мен біртексіз сызықты теңдеудің дербес шешімінің қосындысына тең ( болғандағы) .

Мысал 4. 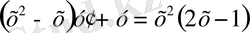теңдеуінің жалпы шешімін тап. Бастапқы шарт у(-2) =2 болғандағы, Коши есебін шеш.

Берілген теңдеуді екі жағын да 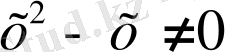өрнегіне бөліп келтіреміз:

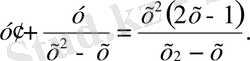
Мұнда

Берілген теңдеудің (6) формуласына сәйкес жалпы шешімі:

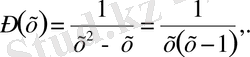
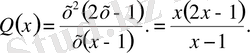
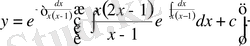(1. 1. 17)

Осы шешімнің ішіндегі интегралдарды шығаралық:

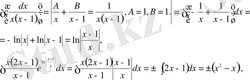
мұндағы 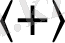және таңбалары 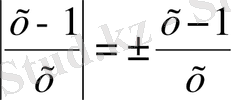теңдігінен шығады. Табылған интегралдарды (7) шешіміне қойсақ, берілген теңдеудің жалпы шешімін аламыз:

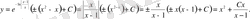
у(-2) =2 бастапқы шартын қанағаттандыратын дербес шешімі:

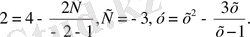
Мысал 5. 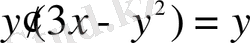теңдеуін шеш.

Шешуі. Бұл теңдеу 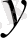-ке қатысты сызықты емес. 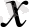-ті у тәуелсіз айнымалысына тәуелді функция ретінде қарастырсақ: 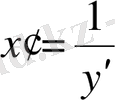. Онда

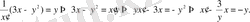
Бұл теңдеу -ке қатысты сызықты .

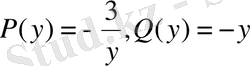(6) -дан,

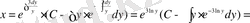
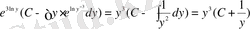
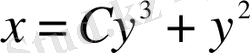- жалпы шешім.

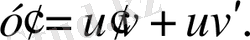
Сонымен қатар, (1. 1. 13) сызықты дифференциал теңдеуін Бернулли әдісін қолданып та, интегралдауға болады. Екі белгісіз функция u(x ), v(x) енгіземіз және y=u(x) v(x) (Бернулли ауыстыруы) деп аламыз. Онда және 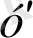өрнектерін (1. 1. 13) теңдеуіне қоя отырып, 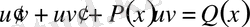немесе

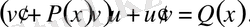(1. 1. 18)

теңдеуін аламыз. Жақшаның ішіндегі өрнекті 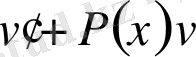=0 десек, бұл айнымалысы ажыратылатын дифференциалдық теңдеу. Осы теңдеуді шешіп, v- ны табуға болады. Енді жақшаның ішіндегі өрнекті нөлге тең деп алғандықтан, (1. 1. 18) теңдеуі мына түрге келеді: 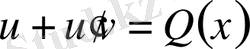. Бұл теңдеуге жоғарыда табылған v- ны қойсақ, бұл да айнымалылары ажыратылатын теңдеу болады, бұл жерден u -ды табамыз. Табылған u мен v- ны Бернулли ауыстыруына қоятын болсақ, берілген теңдеудің жалпы шешімі шығады.

Мысал 6.

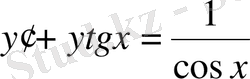
дифференциалдық теңдеуін Бернулли әдісін қолданып шеш және бастапқы шарт 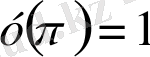болғандағы, Коши есебін шығар.

Бернулли ауыстыруын жасаймыз: 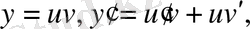онда:

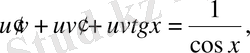
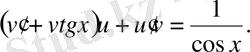
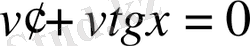теңдеуінің шешімін іздейміз.

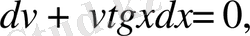
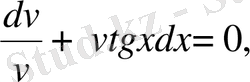
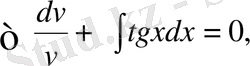
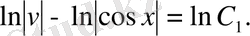
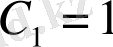деп, шешімін табамыз. Енді 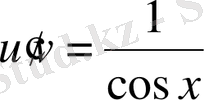теңдеуін шешеміз, мұндағы

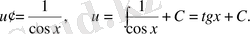
Онда берілген теңдеудің жалпы шешімі:

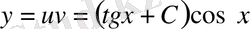
Енді бастапқы шартқа сәйкес дербес шешім іздейміз: 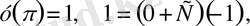бұдан 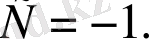Табылған С=-1 мәнін жалпы шешімге қойып, теңдеудің дербес шешімін аламыз: 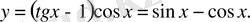[6], [7] .

1. 3 Біртекті дифференциалдық теңдеу

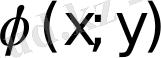функциясы 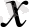пен 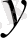бойынша -шы ретті біртекті функция деп аталады, егер кез келге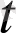н үшін: 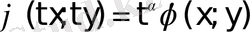теңдігі орындалатын болса.

Егер 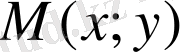және 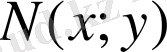- бірдей ретті біртекті функциялар болса, онда (1) теңдеуі біртекті дифференциалдық теңдеу деп аталады.

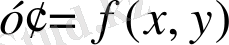теңдеуі біртекті болады, егер 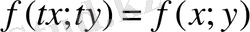, яғни, .

Біртекті дифференциалдық теңдеу айнымалыларды ауыстыру көмегімен айнымалылары ажыратылатын дифференциалдық теңдеуге келтіріледі: 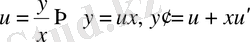немесе .

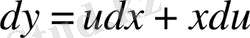Мысал 7. Теңдеуді шеш: .

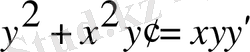Шешуі. Барлығын теңдеудің бір жағына жинақтау арқылы, біртекті дифференциалдық теңдеуге келтіреміз:

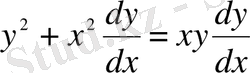
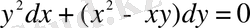
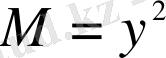және 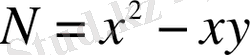- 2-ші ретті біртекті функциялар болғандықтан, теңдеу біртекті дифференциалдық теңдеу. 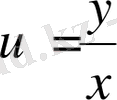белгілеуін енгіземіз.

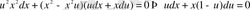- бұл айнымалылары ажыратылатын дифференциалдық теңдеу. Екі жағын да көбейтіндісіне бөліп, интегралдасақ:

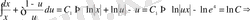
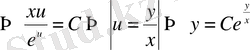- жалпы шешім.

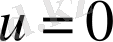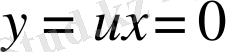және жағдайлары жағдайымен тепе-тең. Жалпы шешімнен С=0 болғанда шығады.

Ескерту . 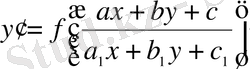түріндегі теңдеу біртекті дифференциалдық теңдеуге келтіріледі.

Мысал 8. 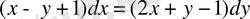теңдеуін біртекті дифференциалдық теңдеу түріне келтір.

Шешуі. Айнымалыларды ауыстырамыз ( 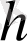және 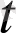- тұрақтылар) :

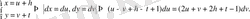
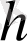және 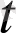-ны бос мүшелері нөлге тең болатындай етіп, таңдап аламыз:

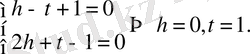
Сонымен, 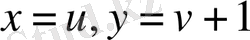деп жаңа айнымалылар енгізсек,

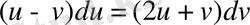түріндегі біртекті дифференциал теңдеуге келеміз.

Мысал 9. 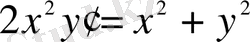дифференциал теңдеуін интегралда және оның у(1) =0 бастапқы шартын қанағаттандыратын дербес шешімін тап.

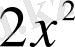және 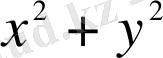функциялары екінші ретті біртекті функция болғандықтан, берілген теңдеу - біртекті. Айнымалыларды ауыстырамыз:

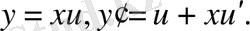
Онда

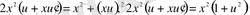
х≠0 деп , теңдеудің екі жағын да 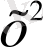-қа бөлеміз:

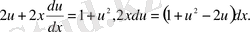
Айнымалыларды ажыратып, екі жағын да интегралдасақ:

.

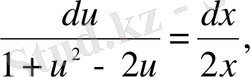
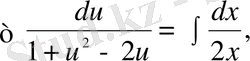
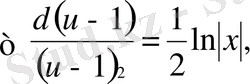
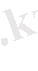
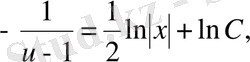
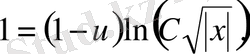Соңғы өрнектегі u- дың орнына у/х -ті қойып, жалпы интегралды аламыз: .

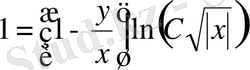
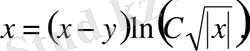Оны у - ке қатысты шешсек, берілген дифференциал теңдеудің жалпы шешімін аламыз:

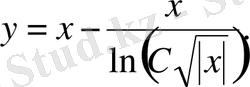
у(1) =0 бастапқы шартын ескере, С тұрақтысын анықталық:

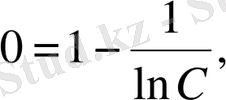
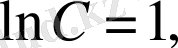
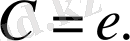
Сонымен, берілген теңдеудің дербес шешімі: 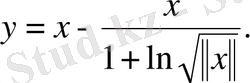[8], [9] .

2 Дифференциалдық теңдеулерді оқытуда ақпараттық-коммуникациялық технологияларды пайдаланудың әдістемелік тәсілдері

2. 1 Дифференциалдық теңдеулерді оқыту кезінде ақпараттық коммуникациялық технологияларды кешенді пайдалану

АКТ-ның негізгі техникалық әдістері

Кесте 1

... жалғасы

Дифференциалдық теңдеу ұғымы

Дифференциалдық теңдеулер туралы жалпы түсінік

Сызықтық дифференциалдық теңдеулер

Жеке туындылардағы дифференциал теңдеулерді шешу жайлы

Дифференциалдық теңдеулер курсында тірек конспектілерін қолдану, және де дифференциалдық теңдеулерді шешу жолдары

N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді шешу әдістері

Екінші ретті сызықтық біртекті теңдеумен Риккати теңдеуінің арасындағы байланыс

Дербес туындылы сызықтық дифференциалдық теңдеулерді зерттеу

Жеке туындылардағы дифференциал теңдеулерді шешу

Екінші ретті сызықтық дифференциалдық теңдеулер теориясы

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс