Импульстің сақталу заңы және кеңістіктің біртектілігі

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Қазақстан Білім және Ғылым Министірлігі

Абай атындағы Қазақ Ұлттық педогогикалық университеті

РЕФЕРАТ

Топ: ФЕК-206

Орындаған: Сапарбекова Мөлдір

Тексерген: Тукен Мадина

Тақырыбы: Сақталу заңдары

2022-2023

Мазмұны

Кіріспе . . . … . . . 2 бет

Негізгі бөлім . . . 3бет

Сақталу заңы . . . ……… . . . … . . . … . . . 3 бет
Импульстің сақталу заңы және кеңістіктің біртектілігі . . . … . . . 4 бет
Импульстің моментін сақтау заңы және кеңістіктің изотропиясы . . . 5 бет
Энергияның сақталу заңы және уақыттың біртектілігі. …… . . . 6 бет

3. Қорытынды . . . … . . . 8 бет

4. Пайдаланылған әдебиеттер . . . …9 бет

Кіріспе

Симметрия принциптері физикалық шамалардың сақталу заңдарымен тығыз байланысты. Кейбір физикалық шамалардың сандық мәндері кез-келген процестерде немесе белгілі бір процестер кластарында уақыт өте келе өзгермейді деген тұжырымдар бар . Шын мәнінде, көптеген жағдайларда сақтау заңдары симметрия принциптерінен туындайды.

Негізгі бөлім

Сақталу заңы

Кеңістік симметриясы мен сақталу заңдары арасындағы байланысты 1918 жылы неміс математигі Эмми Нетер (1882 - 1935) құрды. Ол өзінің атымен аталатын Математикалық физиканың іргелі теоремасын тұжырымдады және дәлелдеді, егер кейбір жүйе кейбір жаһандық түрлендіруге қатысты инвариантты болса, онда ол үшін белгілі бір тұрақты шама бар. [1]

Жалпы салыстырмалылық мәселелері бойынша бүкіл топтың жұмысына қатысу кезінде дәлелденген Нетер теоремасы физикалық теорияны құрудағы симметрия принциптерінің ерекше рөлін бекіткен теориялық физиканың маңызды құралына айналды. Теориялық-инвариантты тәсіл, Эрланген принципі физикаға еніп, Лагранж тілінде физикалық теорияларды тұжырымдаудың орындылығын анықтады деп айтуға болады. Сонымен, аталған сақтау заңдары нақты уақыт кеңістігінде болатын симметриялардың салдары болып табылады. Энергияның сақталу заңы уақытша трансляциялық Симметрияның салдары-уақыттың біртектілігі. Уақыттың біртектілігіне байланысты жабық жүйенің Лагранж функциясы уақытқа тәуелді емес, бірақ осы жүйені құрайтын барлық элементтердің координаттары мен импульстарына байланысты. Қарапайым математикалық түрлендірулермен бұл қозғалыс процесінде жүйенің жалпы энергиясының өзгеріссіз қалуына әкелетінін көрсетуге болады. [2]

Импульстің сақталу заңы кеңістіктің трансляциялық Инварианттылығының (кеңістіктің біртектілігі) салдары болып табылады. Егер Лагранж функциясы кеңістіктегі жабық жүйенің кез-келген шексіз аз тасымалдануымен өзгеріссіз қалуын талап етсек, онда біз Импульстің сақталу заңын аламыз. [2]

Импульстің моментінің сақталу заңы кеңістіктегі бұрылыстарға қатысты Симметрияның салдары болып табылады, кеңістіктің изотроптылығын көрсетеді. Егер Лагранж функциясы кеңістіктегі тұйық жүйенің кез-келген шексіз аз бұрылысында өзгеріссіз қалуын талап етсек, онда біз импульстің моментін сақтау заңын аламыз. Бұл сақталу заңдары барлық бөлшектерге тән, жалпы, барлық өзара әрекеттесулерде орындалады.

Механикада (және жалпы физикада) жиі сақталатын шамалар қозғалыс интегралдары деп аталады. Бірақ сақталудың осы үш заңы әрқашан ерекше ерекшеленеді, өйткені олардың шығу тегі терең мағынаға ие -олар кеңістік пен уақыттың қасиеттерімен, олардың біртектілігімен және изотропиясымен байланысты. Бұл интегралдар үшін қозғалыстар ең маңызды қасиет - аддитивтілік. [3]

Сақталу заңдары кеңістік пен уақыттың біртектілігі мен изотропиясының салдары деген тұжырым жиі кездеседі. Алайда, бұл сақтау заңдарын шығару үшін кеңістік пен уақыт жеткілікті деп ойлау дұрыс болмас еді. Барлық аталған заңдар қозғалыс заңдарының салдары(мысалы, Ньютонның 2-ші Заңы) . Сондықтан мынаны түсіну керек: сақтау заңдарын осы Ньютонның 2-ші заңынан ала аламыз, егерде оған кеңістік пен уақыт симметриясының қасиеттері қосылатын болса. [3]

Уақыттың, кеңістіктің біртектілігі және кеңістіктің изотропиясы дегеніміз не? Енді сұраққа жауап беріп өтсек.

(бірдей жағдайларда алынғанда) -түрлі уақыт аралығында бақыланған физикалық құбылыстардың бірдей өтуі болып табылады. Басқаша айтқанда, олар əртүрлі уақытта өздерінің физикалық қасиеттері бойынша бір-біріне эквивалентті болады.
- ол тұйық жүйе кеңістігіндегі денелерді параллель көшіру кезінде олардың физикалық қасиеттері мен қозғалыс заңдары өзгермейді, басқаша айтқанда инерциялық санақ жүйесінің бастапқы координатасының орнын таңдап алуға тәуелді емес деген тұжырымнан шығады.
- барлық бағыттардың теңдігі. Уақыттың біртектілігі - уақыт бойынша барлық нүктелер тең, артықшылықтықтарының болмауы, кез-келгенін бастапқы деп алуға болады. Координат жүйелері. Координаттар жүйесі - бұл координаттар әдісін жүзеге асыратын анықтамалар кешені, яғни сандардың немесе басқа белгілердің көмегімен нүктенің немесе дененің орны мен қозғалысын анықтау тәсілі. [3]

Импульстің сақталу заңы және кеңістіктің біртектілігі.

Сонымен, кеңістіктің біртектілігіне байланысты жабық жүйенің механикалық қасиеттері жүйенің кеңістіктегі бүтін ретінде кез-келген параллель тасымалдануымен өзгермейді. Жабық жүйе үшін импульстің сақталуы заңы ресми түрде Ньютонның 2-ші және 3-ші заңдарынан туындайды:

$\overrightarrow{F_{ext}} = 0\ \ \ \ және\ \frac{\overrightarrow{dp}}{dt} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$

Алайда, Ньютонның 3-ші Заңы мен Импульстің сақталу заңының әділдігі кеңістіктер біртектілігіне байланысты . Бізде жабық жүйеде жұмыс істейтін ішкі күш $\overrightarrow{F_{i}}$ болсын. Кеңістіктің біттектілігі мынаны білдіреді: кеңістіктегі жүйенің барлық бөлшектерін $\overrightarrow{dr}$ қашықтығына және,

ештеңе өзгерnt алмайтындықтан, барлық ішкі күштердің жұмысы (i-ші бөлшектегі жұмыс $\overrightarrow{F_{i}}\, \ \overrightarrow{dr}$ ), әрқашан потенциалдық энергияның өзгеруіне тең болатын болғандықтан оны 0-ге тең болуы керек. Енді мына шартты жазамыз:

$\overrightarrow{F_{1}\ }, \ \overrightarrow{dr} + \overrightarrow{F_{2}\ }, \ \overrightarrow{dr} + \ldots = \left( \overrightarrow{F_{1}} + \overrightarrow{F_{2}} + \ldots \right) \overrightarrow{dr} = 0\ \ \ \ \ \ \ \ \ \ \ (2)$

немесе басқаша, $i$ бөлшектегі толық күш әрбір басқа бөлшектің күштерінің қосындысына тең екенін еске түсіру арқылы біз мынаны аламыз:

$\overrightarrow{dr}\sum_{i, j}^{}\overrightarrow{F_{ij}} = 0\ \ \ \ \ \ \ \ \ \ \ \ (3)$

$\overrightarrow{dr}\ \$ ға байланысты біз импульстің сақталу заңын аламыз:

$\overrightarrow{F_{1}} + \overrightarrow{F_{2}} + \overrightarrow{F_{3}} + \ldots = 0 = \frac{\overrightarrow{dp}}{dt}; \ \ \ \ \ \ \ \ \ \ p = const\ \ \ \ \ \ \ \ \ (4)$

Бұл өрнекті бақаша жазсақ:

$\sum_{i \neq j}^{}\overrightarrow{F_{ij}} = 0 = \frac{1}{2}\sum_{i \neq j}^{}{(\overrightarrow{F_{ij}}} + \overrightarrow{F_{ji}}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)$

бөлшектердің әрқайсысының бір-бірімен өзара әрекеттесуінің тәуелсіздігіне байланысты біз Ньютонның 3-ші заңын аламыз:

$\overrightarrow{F_{ij}} = - \overrightarrow{F_{ji}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)$

Ескерту 1. Егер бізде импульстің тасымалдаушылары тек материалдық денелер ғана емес, сонымен қатар өріс болса, онда бұл тұжырымда Ньютонның 3-ші заңы қолданылмайды. Өрісті, оның импульсін ескеру керек, содан кейін қайтадан жабық жүйе үшін біз кеңістіктің біртектілік қасиетінен $\overrightarrow{p} = const$ аламыз. [4]

Импульстің моментін сақтау заңы және кеңістіктің изотропиясы.

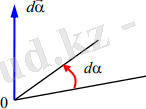Тұйық жүйе үшін сыртқы күштердің моменті нөлге тең ${\overrightarrow{M}}_{ext} = 0$ . Изотропия дегеніміз, егер жабық жүйені кеңістіктегі кез-келген бұрышқа бұрған кезімізде ештеңе өзгермейді (сурет-1) .

$M_{i}$ қозғалмайтын нүктеге қатысты ішкі күштердің моменттері 0 болсын. Біз бүкіл жүйені $d\alpha$ бұрышына бұрамыз. Изотропиядан күш моменттерінің жұмысы нөлге тең болуы керек:

1-сурет. Изотропия сызбасы

$dA = {\overrightarrow{M}}_{1}d\overrightarrow{\alpha} + {\overrightarrow{M}}_{2}d\overrightarrow{\alpha} + \ldots = 0\ \ \ \ \ \ \ \ \ (7) \$

Айналу бұрышының еріктілігіне байланысты $d\alpha$ өлшем ішкі күштердің моменттерінің қосындысы 0-ге тең деп тұжырымдаймыз:

${\overrightarrow{M}}_{1} + {\overrightarrow{M}}_{2} + \ldots = \sum_{i}^{}{\overrightarrow{M_{i}} =}\frac{\overrightarrow{dL}}{dt} = 0\ \ \ \ \ \ \ \ \ \ (8)$

Осыдан импульс моментінің сақталу заңы шығады:

$\overrightarrow{L} = const\ \ \ \ \ \ \ \ (9) \ \ \ \ \ \ \$

Осылайша, импульстің моментінің сақталу заңы кеңістіктің изотропиясымен байланысты деген қорытынды шығарамыз. [4]

Энергияның сақталу заңы және уақыттың біртектілігі.

Динамикадан біз Ньютонның 2-ші Заңының салдарынан - механикалық жүйедегі күштердің жұмысы оның кинетикалық энергиясының $К$ өсуіне тең:

$А_{12} = K_{2} - K_{1}\ \ \ \ \ \ \ \ \ \ \ \ \ (10)$

$i - \ ші\ \ \$ бөлшекке $\overrightarrow{F}\left( F_{x}, F_{y}, F_{z} \right) \$ күші әсер етсін, онда оның компоненттері былай анықталады:

$F_{x} = - \frac{dU}{dx}\ \ \, \ F_{y} = - \frac{dU}{dy}\ \, \ F_{z} = - \frac{dU}{dz}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) \ \ \ \ \$

Жалпы жағдайда $U$ потенциалдық энергиясы (мысалы, ашық жүйе үшін) уақытпенде байланысты $t:\ U\ = \ U(x, y, z, t)$ . Сондықтан $U$ -дің толық өсуі уақыт туындысын да қамтиды (яғни функцияның толық дифференциалы) :

$dU = \frac{dU}{dx}dx + \frac{dU}{dy}dy + \frac{dU}{dz}dz + \frac{dU}{dt}dt. \ \ \ \ \ \ \ \ (12)$

бұл ретте 1 күйден 2 күйге өту кезінде потенциалдық энергияның түпкілікті өсуі интегралмен айқындалады:

$\int_{1}^{2}{dU(x, y, z, t) = U_{2} -}U_{1\ }, \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13)$

мұндағы 1 және 2 негізінен әртүрлі кеңістіктік нүктелер мен әртүрлі уақыттарды білдіруі мүмкін. 1 нүктеден 2 нүктеге кеңістіктік қозғалыс кезіндегі күштердің жұмысын толығырақ жазайық:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.