Сұйық ағынының ламинарлы және турбулентті режимдерін эксперименталды зерттеу


Қазақстан Республикасы Білім және Ғылым министрлігі
Әл-Фараби атындағы Қазақ Ұлттық университеті

Факультет : Механика-математика
Кафедра : Механика
Жоба
Тақырыбы : <<Сұйықтық ағынының екі режимді болуының эксперименталды иллюстрациясы: ламинарлы және турбулентті>>.
Орындаған : Есберген Жандаулет Әмірханұлы
Қабылдаған : Туралина Динара Елеусизовна
Алматы 2022
Мазмұны
I. Кіріспе бөлімі
1. 1 Сұйықтық ағынының режимдері. Ламинарлық және турбулентті режим . . .
1. 2 Ламинарлық және турбулентті қозғалыс режимдеріндегі эксперименттік мәліметтер бойынша Рейнольдс санын анықтау . . .
II. Теориялық бөлім
2. 1 Есептің физикалық қойылымы . . .
2. 2 Есептің математикалық қойылымы . . .
III. Зерттеу әдісі
3. 1 Тәжірибе жасайтын құрылғы туралы анықтама . . .
3. 2 Тәжірибе жұмысы . . .
3. 3 Тәжірибе нәтижесі . . .
IV. Қорытынды
V. Қолданылған деректер тізімі
I. Кіріспе бөлімі
1. 1 Сұйықтық ағынының режимдері. Ламинарлық және турбулентті режим
Гидравликаның дамуының қысқаша тарихы
Гидравлика - сұйық денелердің (тамшы сұйықтықтар мен газдар) қозғалысы мен тыныштық заңдылықтарын және олардың қатты беттерге күш әсерін зерттейтін жалпы инженерлік пән. Гидравлика ғылым ретінде тарихи шартты және адамның суды пайдалануының бүкіл тарихымен тығыз байланысты.
«Гидравлика» сөзі гректің екі сөзінің бірігуінен шыққан: hudor - су және аулос - құбыр, демек, судың құбырлар арқылы қозғалысы туралы ілімді білдіреді.
Архимедтің «Жүзбелі денелер туралы» трактаты (б. з. б. III ғ. ) сұйықтың оған батырылған дененің бетіне түсіретін қысым күші туралы заңын қамтитын гидравлика саласындағы алғашқы ғылыми еңбегі болып саналады. Одан кейін он жеті ғасыр бойы бұл жаңа ашылымдар жасалмады. Гидравликаның қарқынды дамуы өнеркәсіптік капиталдың дамуымен басталды. 15 ғасырдың аяғында Леонардо да Винчи саңылаулардан сұйықтықтың ағуымен айналысып, өзендер мен арналардағы су қозғалысының заңдылықтарын зерттеді. Гидравлика саласында еңбек еткен 16 - 17 ғасыр ғалымдарының ішінен ыдыстың қабырғалары мен түбіне түсетін қысым күштерін есептеу ережесін құрастырған голланд ғалымы С. Стевинді (1585) атаған жөн; Итальяндық ғалымдар - «гидростатикалық парадоксты» ашқан Г. Галилей (1612 ж. ) және саңылаулар арқылы резервуарлардан өтпейтін сұйықтықтың ағу жылдамдығының формуласын алған Э. Торичелли (1640) ; сұйықтардағы ішкі үйкеліс гипотезасын тұжырымдаған және қозғалыстағы ағындардың динамикалық ұқсастық заңын бекіткен ағылшын ғалымы И. Ньютон (1680 ж. ) ; Гидравликаның жекелеген тарауларының дамуында 15 - 17 ғасырлардағы ғалымдар үлкен рөл атқарды, алайда гидравликаның теориялық негіздерін (сұйықтар мен газдардың механикалық қозғалысы туралы ілім) 18 ғасырдың ортасында құрылды. Санкт-Петербург ғылым академиясының Даниил Бернулли, Леонард Эйлер және Михаил Васильевич Ломоносовты айта кеткенім абзал . . .
« Сұйық дене » немесе жай ғана « сұйық » сөзі өтімділікке ие ортаны білдіреді, яғни. ерікті шағын ығысу кернеулерінің әсерінен қайтымсыз ығысу деформациясына қабілеттілік. Сұйықтық - бұл тамшы сұйықтың да, газдың да ортақ қасиеті. Сондықтан «сұйықтық» сөзі екі БАҚ үшін де біріктіреді. Тамшы тәрізді сұйықтықтар мен газдар жылжымалы молекулалардан тұрады. Молекулалардың өздері де, олардың арасындағы бос орындар да сұйықтық қозғалысын зерттеген кезде қарастырылатын көлемдермен салыстырғанда әлдеқайда аз. Демек, нақты сұйықтықты үздіксіз затпен толтырылған кейбір үздіксіз орта ретінде көрсетуге болады. Үздіксіздік гипотезасы нақты суретке ешқандай зиян келтірместен нақты есептерді шешуде үлкен ыңғайлылық береді. Ортаның үздіксіздігі мен үзіліссіздігі моделі сирек газдардың қозғалысын немесе олардың қатты денелер айналасындағы ағынын зерттеуде қолданылмайды. Сұйықтықтар мен газдарды түсіру жан-жақты қысу күштерінің әсерінен басқаша әрекет етеді. Егер газдар олардың көлемін айтарлықтай азайтса, онда тамшы сұйықтықтар өте әлсіз сығылады, сондықтан тамшы сұйықты сығылмайтын, ал газды сығылатын сұйықтық деп атайды.
Сұйықтықтың негізгі физикалық-механикалық қасиеттері.
1. Сұйықтықтың тығыздығы оның көлем бірлігіндегі массасы. (рис б)
2. Меншікті көлем - масса бірлігі алып жатқан көлем.
3 . Меншікті ауырлық - бұл бір нүктедегі сұйықтықтың салмағы және бір нүктеде берілген (рис а)
4. Салыстырмалы тығыздық δ - өлшемсіз шама, тығыздық қатынасына тең , сұйықтықтық тығыздығының меншікті салмағына , t = 4 С кезінде таза судың меншікті салмағына тең :
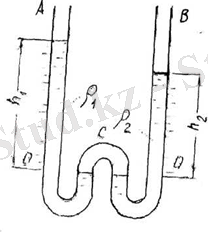
 рис а
рис а
Рис б
Сұйықтықтың тұтқырлығы
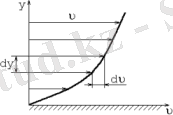 Сұйықтың қозғалысын зерттеуде ерекше рөл атқаратын маңызды қасиеттерінің бірі - тұтқырлық. Тұтқырлық (ішкі үйкеліс) сұйықтықтың ығысуға қарсы тұру қасиеті. Тұтқырлықтың баяулататын әсерінен сұйықтықтың жылдамдығы қабырғаға жақындаған сайын азаяды. (рис1)
Сұйықтың қозғалысын зерттеуде ерекше рөл атқаратын маңызды қасиеттерінің бірі - тұтқырлық. Тұтқырлық (ішкі үйкеліс) сұйықтықтың ығысуға қарсы тұру қасиеті. Тұтқырлықтың баяулататын әсерінен сұйықтықтың жылдамдығы қабырғаға жақындаған сайын азаяды. (рис1)
Бұдан шығатыны, сұйықтық қозғалған кезде сұйықтықтың кейбір қабаттары басқаларға қатысты сырғанайды. Нәтижесінде сұйықтықтың қозғалысына қарсы тұратын үйкеліс күші пайда болады. Тұтқырлық Ньютонның тұтқыр (ішкі) үйкеліс заңымен өлшенеді.
-ішкі үйкеліс күштерінің кернеуі ( тангенциалды кернеу күш импульсінің өзгеруі туралы теореманы қолданғанда күш импульсінің меншікті ағыны ретінде де қарастырылуы мүмкін
-динамикалық тұтқырлық коэффициенті, ол сұйықтық түріне, температураға және қысымға байланысты
-жылдамдық градиенті
y - қозғалыс бағытына нормаль координат [м]
Ламинарлық сұйықтық ағынының режимдерін суреттеуге арналған орнату схемасы 2суретте көрсетілген. Кран арқылы мөлдір құбыр арқылы резервуардан сұйықтық ағызуға түседі. Құбырға кіретін жерде жұқа түтік орнатылады, ол арқылы бояғыш зат ағынның орталық бөлігіне енеді. Егер сіз шүмекті аздап ашсаңыз, сұйықтық құбыр арқылы төмен жылдамдықпен ағып кете бастайды. Ағынға бояу агентін енгізу арқылы сызық түріндегі бояу агентінің ағымдағы ағыны құбырдың басынан аяғына дейін қалай ағып жатқанын көруге болады. Бұл сұйықтықтың араласусыз және құйынды түзілмей қатпарлы ағуын және ағындағы инерция күштерінің басымдылығын көрсетеді. Ламинарлық ағында ағындар құбыр осіне параллель болады, яғни. сұйықтық ағынына көлденең қозғалыс жоқ. Бұл ағын режимі ламинарлы деп аталады.
 Ламинарлық ағын
- сұйықтың бөлшектердің араласуынсыз, жылдамдықтар мен қысымдардың пульсациясынсыз, қабаттар мен құйындылардың араласуынсыз қабатталған ағыны.
Ламинарлық ағын
- сұйықтың бөлшектердің араласуынсыз, жылдамдықтар мен қысымдардың пульсациясынсыз, қабаттар мен құйындылардың араласуынсыз қабатталған ағыны.
Турбуленттік ағын
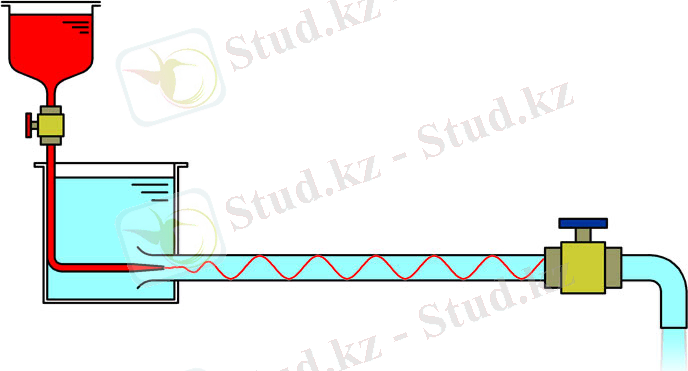 Қарастырылып отырған қондырғыда құбыр арқылы өтетін ағын жылдамдығының жоғарылауымен сұйық бөлшектердің қозғалыс жылдамдығы артады. Бояғыш сұйықтық ағыны тербеле бастайды.
Қарастырылып отырған қондырғыда құбыр арқылы өтетін ағын жылдамдығының жоғарылауымен сұйық бөлшектердің қозғалыс жылдамдығы артады. Бояғыш сұйықтық ағыны тербеле бастайды.
 Егер сіз кранды көбірек ашсаңыз, құбыр арқылы өтетін ағын артады.
Егер сіз кранды көбірек ашсаңыз, құбыр арқылы өтетін ағын артады.
Бояғыш сұйықтықтың ағыны негізгі ағынмен араласа бастайды, құйынды түзудің және араласудың көптеген аймақтары байқалады, ағында инерция күштері басым болады.
Турбулентті ағында жылдамдық векторлары тек осьтік емес, сонымен қатар арна осіне қалыпты құрамдас бөліктерге ие. Бұл ағын режимі турбулентті деп аталады. Турбуленттік режим - қарқынды араласумен, қабаттардың бір-біріне қатысты жылжуымен және жылдамдықтар мен қысымдардың ауытқуымен жүретін ағын.
 Немесе бұл екі ағынды былай түсіндірсе болады:
Немесе бұл екі ағынды былай түсіндірсе болады:
Сұйық ағынның ламинарлы (а) және турбулентті (б) ағыны
(а) жағдайда түсті сұйықтық ағыны өзгермеген пішінді сақтайды және сұйықтықтың қалған бөлігімен араласпайды. (b) жағдайда түрлі-түсті ағын кездейсоқ құйындылармен үзіледі, олардың үлгісі уақыт бойынша өзгереді. «Ағындық түтік» түсінігі турбулентті ағынға қолданылмайды.
Ламинарлық ағын - сұйық қабаттары араласпай, бір-біріне қатысты сырғанап ағып өтетін ағын. Ламинарлық ағын стационарлық - кеңістіктегі әрбір нүктедегі ағынның жылдамдығы тұрақты болып қалады. Радиусы R және ұзындығы L құбырдағы Ньютон сұйықтығының ламинарлы ағынын қарастырайық, оның ұштарындағы қысымдары тұрақты ) . Радиусы r цилиндрлік ток түтігін бөліп алайық.
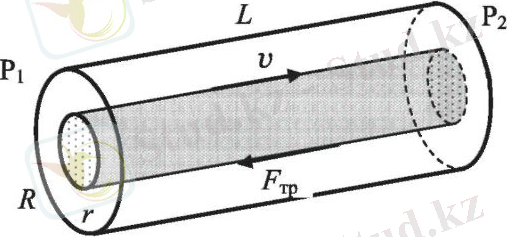
Ағын түтігі және оған әсер ететін үйкеліс күші
Бұл түтіктің ішіндегі сұйықтыққа қысым күші және тұтқыр үйкеліс күші әсер етеді.
Ағын стационарлық болғандықтан, бұл күштердің қосындысы нөлге тең:
бұл мәнді формулаға ауыстырып, ағын жылдамдығының түтік осіне дейінгі қашықтыққа тәуелділігін аламыз: (ламинарлы ағын )
Турбулентті ағын - сұйық бөлшектерінің әрбір нүктедегі жылдамдықтары кездейсоқ өзгеретін ағын. Бұл қозғалыс дыбыстың пайда болуымен бірге жүреді. Турбулентті ағын - сұйықтықтың ретсіз, өте ретсіз, ретсіз ағыны. Сұйық элементтер күрделі ретсіз траекториялар бойымен қозғалады, бұл қабаттардың араласуына және жергілікті құйындылардың пайда болуына әкеледі.
Турбулентті ағынның құрылымы - бұл негізгі «орта ағынға» қабаттасқан өте үлкен мөлшердегі шағын құйындылардың тұрақсыз жиынтығы. Бұл ретте белгілі бір уақыт аралығында орташа есеппен ғана бір бағытта немесе басқа бағытта ағын туралы айтуға болады.
Турбулентті ағын сұйықтық қозғалысы кезінде қосымша энергия шығынымен байланысты: энергияның бір бөлігі хаотикалық қозғалысқа жұмсалады, оның бағыты ағынның негізгі бағытынан ерекшеленеді, бұл қан жағдайында жүректің қосымша жұмысына әкеледі. Қанның турбулентті ағыны нәтижесінде пайда болатын шуды ауруды диагностикалау үшін пайдалануға болады. Бұл шу, мысалы, қан қысымын өлшеу кезінде иық артериясында естіледі.
Турбулентті ағынның маңызды қасиеті (ламинарлық ағынмен салыстырғанда) ағынның жоғары кедергісі болып табылады. Егер турбуленттікті «сөндіру» мүмкін болса, онда кемелердің, суасты қайықтарының және ұшақтардың қозғалтқыштарының қуатын айтарлықтай үнемдеуге қол жеткізуге болады.
1. 2 Ламинарлық және турбулентті қозғалыс режимдеріндегі эксперименттік мәліметтер бойынша Рейнольдс санын анықтау
Ағылшын физигі Осборн Рейнольдс табиғатта сұйықтық қозғалысының әртүрлі түрлерінің бар екенін өте айқын көрсететін эксперименталды зерттеулерінің нәтижелерін жариялады. Тәжірибе көрсеткендей, сұйық немесе газ қозғалысының екі режимі мүмкін: ламинарлы және турбулентті.
Ламинарлық (параллель ағынды) қозғалыс жеке бөлшектердің араласусыз және жылдамдық пен қысым пульсацияларысыз реттелген қозғалысымен сипатталады . Егер сұйықтық ламинарлы қозғалыс режимінде тұрақты көлденең қиманың түзу құбырында ағып кетсе, онда барлық ағындар құбырдың осіне параллель бағытталған, яғни. түзу сызықты болады және оның ағуы кезінде сұйықтықтың көлденең қозғалысы болмайды.
Турбулентті (хаотикалық) қозғалыс сұйықтық бөлшектерінің қарқынды араласуымен және жылдамдықтар мен қысымдардың ауытқуымен сипатталады. Турбулентті қозғалыс кезіндегі жекелеген бөлшектердің траекториялары күрделі қисық пішінге ие, бұл турбулентті қозғалыс кезінде сұйықтықтың құбыр бойымен негізгі бойлық қозғалысымен бірге жеке сұйық объектілерінің көлденең қозғалыстары мен айналмалы қозғалысының болатынын көрсетеді.
Ламинарлық режим негізінен тұтқыр сұйықтықтардың (май, майлау майлары және т. б. ) қозғалысы кезінде, сондай-ақ судың жұқа капиллярлар арқылы қозғалуы кезінде байқалады. Су құбырларында, қысымды өткізгіштердің әртүрлі типтерінде, каналдар мен өзендерде және т. б. судың қозғалысы әдетте тәжірибеде кездесетін жылдамдықтарда, ағын әрқашан дерлік турбулентті режимдермен сипатталады. Сұйықтық ағынының режимі оның жылдамдығына байланысты және берілген құбырдағы ламинарлы ағыннан турбулентті ағынға ауысуы белгілі бір жылдамдықта жүреді, бұл санның сапаға ауысуының философиялық заңының растауы болып табылады. Эксперименттік зерттеулер нәтижелерін талдау негізінде Рейнольдс Рейнольдс саны (критерий) деп аталатын өлшемсіз коэффициентті ұсынды:
d - құбыр диаметрі v - сұйықтық тұтқырлығының кинематикалық коэффициенті.
Тәжірибелердің нәтижесінде Рейнольд дөңгелек құбыр үшін сұйықтық ағынының режимдері өзгеретін критикалық сан = 2320 болатынын анықтады. Содан кейін Re < үшін сұйықтық ағыны ламинарлы, ал Re > , ол турбулентті.
Рейнольдс эксперименттік қондырғысының схемасы 3-суретте көрсетілген
Сұйықтық шыны түтікке 1 қысым резервуарынан түседі 2. Құбырдың көмегімен 3 шүмекпен толтырылады 4. Тұрақты қысым (сұйықтықтың бос бетінің деңгейі) су төгетін құбырды орнату арқылы сақталады 5. құбырдағы 1 сұйықтықтың шығынын өзгерту кранмен орындалады 6. Өлшеу ыдысы 7 сұйықтықтың шығынын анықтау үшін қызмет етеді. 1-құбырдағы сұйықтық ағынының режимін визуалды бақылау үшін оған капиллярлық түтік 8 арқылы 10 кранымен 9 резервуардан тоналды сұйықтық беріледі
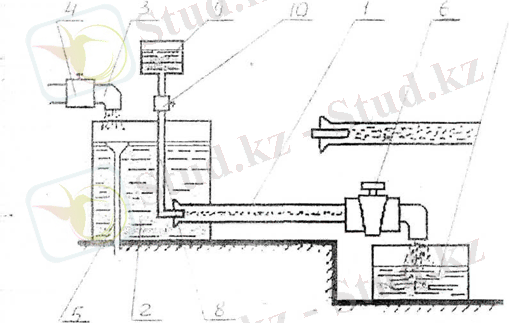 Рисунок 3
Рисунок 3
Эксперименттік процедурасы
Екі түрлі сұйықтық үшін біз кранмен 6 бес шығын жылдамдығын орнатамыз, біз оны өлшеу цистернасы 7 ( Вт - су көлемі) және секундомер ( t - өлшеу цистернасының толтыру уақыты W ) арқылы өлшейміз. Сұйықтықтың шығыны ( Q ) тәуелділікпен анықталады:
Эксперименттік мәліметтерді тіркеу
- Өлшеу ыдысына түсетін судың көлемі В
- Толтыру уақыты t (с)
- Ағын жылдамдығын мына формуламен табамыз:ρ=mV\rho = \frac{m}{V}
- Құбыр диаметрінің 1 ( d ) мәнін біле отырып және оның көлденең қимасының ауданын ( s ) анықтай отырып, сұйық ағынының жылдамдығының ( V ) мәнін мына қатынас арқылы табамыз :
v - сұйықтықтың тұтқырлығының кинематикалық коэффициенті,
- 𝛄=𝐆𝐕\mathbf{\gamma =}\frac{\mathbf{G}}{\mathbf{V}}\қатынасты пайдаланып, әртүрлі жылдамдықтағы екі түрлі сұйықтық үшін Re мәнін анықтаймыз және алынған мәндерді 1-кестеде қорытындылаймыз.
Кесте 1
№ p/p
v м 2 / с
Дизайн параметрлері
V, м/с
Re
- Алынған нәтижелерге сүйене отырып, біз бірдей координаталар жүйесіне екеуін саламыз: Re = f ( V ) тәуелділігінің графигін (әртүрлі сұйықтықтар үшін) және қорытынды жасаймыз.
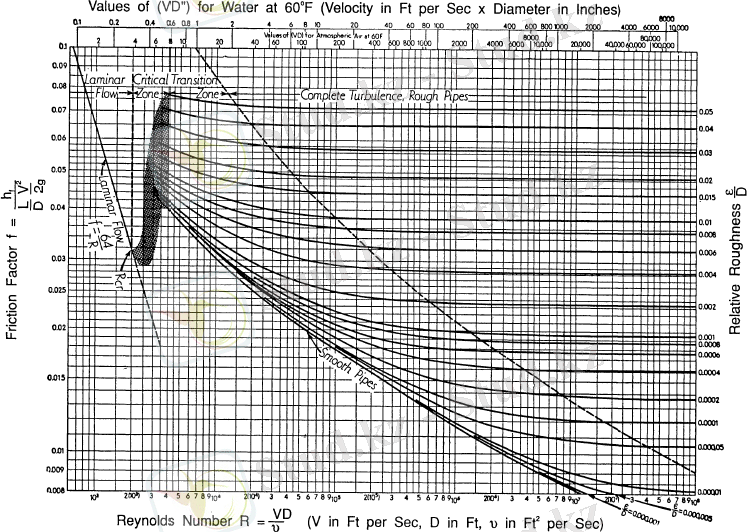
Рейнольдс сандарын Moody диаграммасы арқылы ыңғайлы түрде анықтайды.
II. Теориялық бөлім
2. 1 Есептің физикалық қойылымы
Сұйықтықтың тұтқырлығын өлшеу әдістерінің жиынтығы вискозиметрия деп аталады. Тұтқырлықты өлшейтін құрылғы вискозиметр деп аталады . Тұтқырлықты өлшеу әдісіне байланысты вискозиметрлердің келесі түрлері қолданылады:
- Оствальд капиллярлық вискозиметрі Пуазейль формуласына негізделген. Тұтқырлық белгілі бір қысымның төмендеуі кезінде ауырлық күшінің әсерінен капилляр арқылы белгілі массасы бар сұйықтықтың ағуына кететін уақытты өлшеу арқылы анықталады.
- Екі сұйықтық қозғалатын екі капилляры бар медициналық Гесс вискозиметрі (мысалы, тазартылған су және қан) . Бір сұйықтықтың тұтқырлығы белгілі болуы керек. Сұйықтықтардың бір уақыттағы қозғалысы олардың тұтқырлығына кері пропорционал болатынын ескере отырып, екінші сұйықтықтың тұтқырлығы есептеледі.
- Стокс әдісіне негізделген вискозиметр, оған сәйкес R радиусы бар шар тұтқырлығы η сұйықтықта төмен v жылдамдықпен қозғалғанда, кедергі күші осы сұйықтықтың тұтқырлығына пропорционал болады: F = 6πηRv (Стокс формуласы ) . Қызыл қан жасушалары тұтқыр сұйықтықта - қан плазмасында қозғалады. Эритроциттер диск тәрізді және тұтқыр сұйықтыққа шөгетіндіктен, олардың шөгу жылдамдығын (ШТҚ) шамамен Стокс формуласы бойынша анықтауға болады. Шөгу жылдамдығы шөгінді эритроциттердің үстіндегі плазма мөлшерімен бағаланады. Қалыпты жағдайда эритроциттердің шөгу жылдамдығы әйелдерде 7-12 мм/сағ, еркектерде 3-9 мм/сағ.
- Айналмалы вискозиметр(рис 4) екі коаксиалды (коаксиалды) цилиндрден тұрады. Ішкі цилиндрдің радиусы R, сыртқы цилиндрдің радиусы R+ΔR (ΔR≤R) .
Рисунок 4
- Цилиндрлер арасындағы кеңістік өзектер белгілі h биіктікке дейін зерттелетін сұйықтықпен толтырылады. Содан кейін ішкі цилиндр белгілі бір күш моментін қолдану арқылы айналуға келтіріледі және тұрақты күйдегі жылдамдық ν өлшенеді. Сұйықтықтың тұтқырлығы формула бойынша есептеледі:
- Айналмалы вискозиметрдің көмегімен ротордың айналуының әртүрлі бұрыштық жылдамдықтарында тұтқырлықты өлшеуге болады. Бұл әдіс тұтқырлық пен жылдамдық градиенті арасындағы байланысты орнатуға мүмкіндік береді, бұл Ньютондық емес сұйықтықтар үшін маңызды.
Пуазейль формуласы
Радиусы R және ұзындығы L құбыр арқылы сұйықтың ламинарлы ағыны кезінде көлденең құбыр арқылы бір секундта өтетін сұйықтықтың Q көлемін келесідей есептеуге болады. Радиусы r және қалыңдығы dr болатын жұқа цилиндрлік қабатты таңдаймыз.
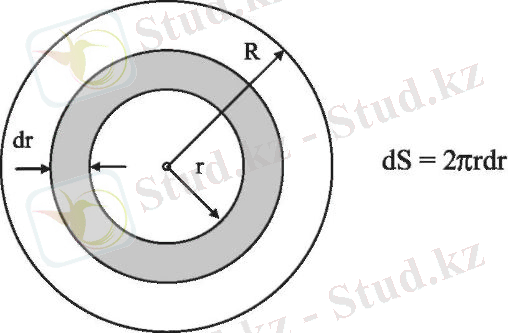 Таңдалған сұйық қабаты бар құбырдың көлденең қимасы
Таңдалған сұйық қабаты бар құбырдың көлденең қимасы
Оның көлденең қимасының ауданы dS = 2πrdr. Жұқа қабат таңдалғандықтан, ондағы сұйықтық бірдей v жылдамдықпен қозғалады. Бір секундта қабат сұйықтық көлемін береді:
Осы жерде цилиндрлік сұйық қабаттың жылдамдығының формуласын ауыстырып, аламыз.
Пуазейль формуласын қорытып шығарамыз:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz