Дифференциалдық және интегралдық есептеулерді оқытудың әдістемесі


Ф. 7. 04-01
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М. ӘУЕЗОВ атындағы ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

«Жаратылыстану ғылымдары және педагогикасы» жоғары мектебі
«Математика» кафедрасы
КУРСТЫҚ ЖҰМЫС
Тақырыбы: Дифференциалдық және интегралдық есептеудің элементтерін оқыту әдістемесі
Пәні
Мамандығы: 5В010900- Математика
Орындаған: Әуез Самал Дарханқызы Группа: ЕП-17-1тк
Жетекші: ф-м. ғ. к. доцент Абжапбаров А.
Жұмыс бағасына қорғалды
«» 2020ж
Норма бақылау:
Комиссия
Шымкент 2020 ж.
Ф. 7. 04-03
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М. ӘУЕЗОВ атындағы ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
«Математика» кафедрасы
№Тапсырма
Комплекс талдау пәні бойынша курстық жұмыс
Студент Әуез Самал Дарханқызы Топ ЕП-17-1тк
Жұмыс тақырыбы
Берілген мәліметтер:
Түсіндірме жазбасының мазмұны
(курстық жұмыс)
Ұсынылған әдебиеттер:
1
2
3
Тапсырма берілген күні
Жұмысты қорғау күні
Жұмыс жетекшісі
Тапсырманы орындауға қабылдаған
Мазмұны
Кіріспе . . .
1. Дифференциалдық есептеулерді оқытудың теориялық негіздері . . .
1. 1. Дифференциалдық есептеудің математика ғылымындағы орны … . . .
1. 2. Дифференциалдық есептеулерді арнайы оқытудың педагогикалық және психологиялық мазмұны … . . .
2. Дифференциалдық(туынды) есептеулер. Туынды табу ережелері . . .
2. 1. Дифференциалдық есептеулердің геометриялық және механикалық мағынасы . . .
2. 2. Функцияның дифференциалы. Лопиталь-Бернулли ережесі . . .
3. Мектепте интеграл тақырыбын тереңдетіп оқытудың әдістемесі . . .
3. 1 Интегралдың шығу тарихы . . .
3. 2 Алғашқы функция мен интегралды оқыту әдiстемесi . . .
4. Алғашқы функция және анықталмаған интеграл. Қисықсызықты трапецияның ауданы . . .
4. 1. Анықталған интеграл. Ньютон-Лейбниц формуласы . . .
4. 2. Рационал, иррационал және тригонометриялық функцияларды интегралдау . . .
4. 3. Алынбайтын интегралдар жөнінде түсінік . . .
4. 4. Геометриялық және физикалық есептерде интегралды қолдану . . .
Қорытынды . . .
Пайдаланылған әдебиеттер тізімі . . .
Кіріспе
Қазақстан Респубикасының білім беру реформаларының негізгі мақсаты жалпы білім-беру жүйесін әлеуметтік-экономикалық ортаға барынша бейімдеу. Ал, білім беру жүйесін барынша жетілдіру осы мақсатқа жасалар алғашқы қадам.
Қазіргі қоғамда барлық мамандық иелерінен белгілі бір дәрежедегі математикалық сауаттылық талап етіледі. Бұл - математика ғылымының қоғамдағы айқын орнының, математика пәнінің дәрежесінің, математика білімінің қаншалықты құнды екендігінің дәлелі. Яғни, мектеп бағдарламасы мен ЖОО -ында берілген барлық математика тақырыптарының түрлі ғылымдарды игеруі мен дамуына үлесі зор.
Қазіргі таңда мектеп бағдарламаларында дифференциал (туынды) және интеграл есептеу лер жайлы көптеген мәліметтер қарастырылған. Яғни, туынды дегеніміз не, алғашқы функцияны қалай есептейміз, теңдеудің шешу жолдары және оны түрлі бағыттағы есептерді шығаруда қалай қолданамыз және тағы басқа сұрақтарды қарастырады.
Дифференциалдық және интегралдық
есептеу
лер оқушылар мен студенттердің негізгі дайындығында, жалпы алғанда, оқушы мен студенттің ғылыми дүниетанымы мен ой-өрісін дамытуда, математикалық мәдениеттің негізін қалауда өте маңызды қызмет атқарады.
Курстық жұмыстың тақырыбының өзектілігі :
- дифференциалдық және интегралдық
есептеу
лер оқушылар мен студенттердің математикалық біліміне зор үлесін тигізеді.
- дифференциалдық және интегралдық есептеулер мектептің математика пәнін оқыту әдістемесіне арналған зерттеулердің кейбір кемшіліктерін толықтырады.
Курстық жұмыстың жаңалығы:
Дифференциалдық және интегралдық есептеулер теориясының мазмұны абстрактілі, жалпы айтқанда теориялық және терең ойлауды, шығамашылық қабілеттің жоғары деңгейде болуын талап етеді. Есептеулердің қабілетті жетілдіруге үлкен ықпалы бар екені де даусыз. Жетілдіру арқылы оқушылардың ой-өрісі мен қарым-қабілеттерін, шығармашылық тұстарын дамытуға жол ашылады.
Жұмыстың мақсаты : Дифференциалдық және интегралдық есептерді шығарудың теоремалары мен анықтамаларын зерттеу, негізгі ережелері мен әдістемесін жинақтау, тақырып аясында зерделеу жұмыстарын жүргізу.
Зерттеудің міндеттері:
-дифференциалдық (туынды) және интегралдық есептеулер теориясыны мазмұны теориялық ойлауды міндеттейді;
-шығармашылық қабілетті шыңдауды және ой өрісін жетілдіруді міндеттейді.
Зерттеу нысаны: Дифференциалдық және интегралдық есептеулерді оқыту жүйесі
Зерттеу әдістері: Тақырыпқа байланысты барлық мәліметтер мен тақырыптарды жинақтау, анықтамалар мен ережелердің мәнін ашып түсіндіру.
Курстық жұмыстың практикалық құндылығы: Дифференциалдық және интегралдық теңдеулер мен олардың әдістемесін жетік меңгеру, бізге өзіміз өмір сүретін ғаламды толық тану үшін жол ашады, нақтырақ айтқанда физика және математика ғылымын кеңінен тануға және ғылыми таным мен түсініктің қалануына жол көрсетеді.
1. Дифференциалдық теңдеулерді оқытудың теориялық негіздері
1. 1. Дифференциалдық теңдеудің математика ғылымындағы орны
Дифференциалдық теңдеу математика ғылымында айрықша ұғым болып есептелінеді. Дифференциалдық теңдеу дегеніміз теңдеудің туындылары берілген алғы шарттарды қанағаттандыратын теңдеу болып табылады. Егер нақты құбылысты немесе белгілі бір үдерісті зерттеу кезеңінде алынған дифференциалдық есептеулер «дифференциалдық модель» деп атайды.
Дифференциалдық модель - өзімізді қоршаған тіршілік әлемін түсінуге және үйренуге құрылатын математикалық модельдердің дербес(жеке) жағдайы. Дифференциалдық есептеулермен сипатталатын дифференциалдық модельдердің ерекшелігінің бір түрі - теңдеулерде кездесетін белгісіз функциялар тек қана бір айнымалыға тәуелді болып табылады.
Жалпы дифференциалдық модельдерді құру үдерісінде зерттеліп және қолданылып жатқан есептеулердің табиғатқа қатысты ғылыми тұжырымдары мен заңдарын білу аса зор маңызға ие. Мысалға алар болсақ, физика ғылымында(механикада) - Ньютон заңдары, химиялық реакция жылдамдығы теориясында - «Салмақтың әсер ету заңы», электрлік тізбектікте - «Кирхгоф заңдары» және тағы басқалары.
Алайда іс жүзіне келгенде дифференциалдық есептеулерді құруға мүмкіндік тудыратын, бірақ белгісіз заңдар да кездеседі, сол себепті өлшемдердің аз ғана өзгеруінде үдерістің жүруіне байланысты түрлі гипотезаларға(жорамалдар) сүйенуге тура келеді.
Кейбір есептеулерде дифференциалдық теңдеулерді тұйық қалпында(формада) шығаруға болады. Бұл дегеніміз элементар функциялар мен қарапайым теңдеулердің шешімін «аналитикалық формула» түрінде шешу.
Дифференциалдық есептеулерді шешу үшін қандайда бір шексіз қатарларды пайдалануға болады, бірақ бұл есептеу түрі тұйық формамен салыстырғанда көбірек теңдеулерді шешуге тура келтіреді.
Көрсетілген мысалдарда айтылғандай, дифференциалдық есептеулердің өзін шығармай ақ, теңдеу шешімдерінің қасиеттері туралы мәліметтер алуға мүмкіндік тудыратын әдіс-тәсілдердің бар екендігі және оның керек екендігі айқын.
Дифференциалдық есептеу лер математика ғылымында айырықша орынға ие. Дифференциалдық есептеулердің сапалық теориясы 19-ғасырдың соңынан бастап қарқынды дамып келеді. Бұл салаға зор еңбегі сіңген француз математигі - Жюль Анри Пуанкаре және орыс математигі - Александр Михайлович Ляпуновтың зерттеулері дифференциалдық теңдеулердің дамуына үлкен пайдасын тигізген.
1. 2. Дифференциалдық теңдеулерді арнайы оқытудың
педагогикалық және психологиялық мазмұны
Математика пәнін оқытудың басты мақсатының бірі - ол оқушыларды және студенттерді ғылыми дүниетануға тәрбиелеу болып саналады. Ал бұл мақсатты орындау барысында дифференциалдық теңдеулер тақырыбы пайдалы және тиімді болмақ.
Қазіргі таңда, барлығына белгілі жағдай математика ғылымын игерудің кез-келген деңгейінде, мектептерде, колледждерде, жоғары оқу орындарында және тағы басқа оқу орындарында әрқашан түрлі бағыттағы оқытудың әдістемелерімен байланыстырады. Бұл акпект, яғни құбылыс метематика ғылымының тарихи қалыптасу үдерісінде оқушы немесе студентің санасында әрдайым нақты және кеңінен түсінік қалыптастырады. Математика пәнін қоршаған ортамен, өмірмен, қоғамдағы болып жатқан іс-әрекеттермен байланыстырып, практикадағы математика ғылымының орны мен қазіргі кездегі ғылыми білімнің математизациялануын талқылап отырады.
Жаратылыстану - математика ғылымыдарының әдістемесінің дифференциалдық есептеулермен байланысын және дифференциалдық теңдеулердің әдістемелік бағытын көруге мүмкіндік ашатын «дифференциалдық теңдеулер теориясы» бағытының тарихи даму жағдайын зерттейтін боламыз. Бұл бағыт бойынша Қазақстан, Ресей және тағы басқа ТМД мемлекеттерінің ғалымдары өз зерттеулерімен зор пайдасын тигізген.
Математика ғылымын меңгертудің түрлі мәселерін математик-ғалымдары мен әдіскерлер қарастырған. Бұл теориялық негіздемелер орыс және кеңес математигі- Болтянский Владимир Григорьевичтің, кеңес математигі -Елена Сергеевна Вентцельтің, кеңес және орыс математигі, педагог- Башмаков Марк Ивановичтің, Баврин Иван Ивановичтің және тағы басқа көптеген ғалымдардың ғылыми еңбектерінде жазылған.
Оқыту үдерісінде қолданбалы бағыттарды пайдалану математика ғылымының негізін білуге ғана емес, ғылыми таным тәсілін үйренуге де әсер береді. Дифференциалдық есептеулердің қолданбалы бағыты оқушының нақты үдерісті матемтикалық модельмен байланыстыру практикасын меңгереді.
Математикалық модельдеу дегеніміз - нақты берілген есептерді математикалық тілге аудару.
Математикалық модельдеу тәсілдерінің қарапайым үдерістерінің арқасында оңай түсінуге және үдерістің сандық және сапалық қасиеттерін белгілеуге мүмкіндік туғызады.
Математикалық модельдеу таным іс-әрекетінің ажырамас бір бөлігі. Математикалық модельдеудің психологиялық құбылысы - тұлға ойында сыртқы және ішкі әлемнің байланысымен ғана есептелмейді. Соңғы кезеңдерде психикалық іс-тәжірибе модельдеу арқылы жүзеге асырылу үстінде. Модельдеу адам миының бір құбылысы ретінде түрліше ұғымдар қарастырып отырады. Көптеген ғалымдар модельдеуді адамдардың қоршаған ортамен байланысын, қарым-қатынасын психикалық іс-тәжірибенің арқасы деп қарастырды.
Сонымен, дифференциалдық есептеулер білім алушыға қоршаған орта туралы түсінік қалыптастыруға көмек көрсететін дүниетанымық және әдістемелік құбылыс. Белгілі бір мөлшерде бұл тақырыпқа тарихи және математикалық бағыт та ықпал жасайды.
2. Дифференциалдық (туынды) теңдеулер. Туынды табу ережелері
Туынды анықтамасы.
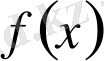 функциясы І аралығында анықталсын. Егер
x
0
∈І үшін
функциясы І аралығында анықталсын. Егер
x
0
∈І үшін
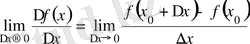 ақырлы шегі бар болса, онда ол шекті
ақырлы шегі бар болса, онда ол шекті
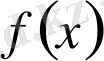 функциясының
x
0
нүктесіндегі туындысы
деп,
функциясының
x
0
нүктесіндегі туындысы
деп,
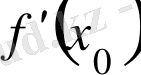 бейнесімен белгіленеді.
бейнесімен белгіленеді.
Туындыны табу амалын функцияны дифференциалдау деп атаймыз. Анықтама бойынша
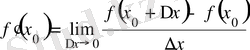 .
.
Өзгеше түсіндірер болсақ, қарапайым тілде анықтама осылай оқылады: Егер функцияның өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының соңғы өсімше нольге ұмтылғанда ақырлы шегі бар болса, онда функцияны дифференциалданатын деп, сол шекті функцияның туындысы деп атайды.
Дәл осы сияқты,
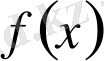 функциясының
х
0
нүктесіндегі сәйкес сол және оң жақты туындыларының анықтамасына келеміз:
функциясының
х
0
нүктесіндегі сәйкес сол және оң жақты туындыларының анықтамасына келеміз:
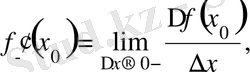
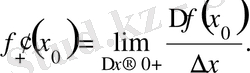
Сондықтан,
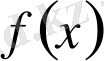 функциясында
х
0
нүктесінің туындысы бар болуы үшін, функцияның сол нүктеде оң және сол жақты туындылары бар болады және ол функциялар бір-біріне тең болу шарттары қажетті және жеткілікті.
функциясында
х
0
нүктесінің туындысы бар болуы үшін, функцияның сол нүктеде оң және сол жақты туындылары бар болады және ол функциялар бір-біріне тең болу шарттары қажетті және жеткілікті.
Дифференциалдау ережелері.
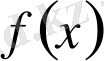 және
және
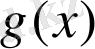 функциялары дифференциалданатын(туындалатын), ал
с
түрақты сан болса, төменде көрсетілген дифференциалдау ережелері орындалады:
функциялары дифференциалданатын(туындалатын), ал
с
түрақты сан болса, төменде көрсетілген дифференциалдау ережелері орындалады:
1.
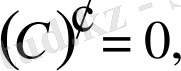 2.
2.
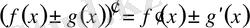 ,
,
3.
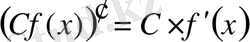 , 4.
, 4.
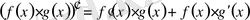 ,
,
5.
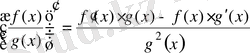
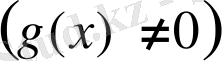 .
.
2. 1. Дифференциалдық теңдеулердің геометриялық және механикалық мағынасы
2. 2. Лопиталь-Бернулли ережесі
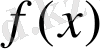 функциясының
х
0
нүктесiндегi туындысының бар болуы, оның графигiнiң
функциясының
х
0
нүктесiндегi туындысының бар болуы, оның графигiнiң
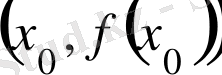 нүктесiнде жанаманың бар болуымен бара бар. Бұл жағдайда,
жанаманың бұрыштық коэффициентi
нүктесiнде жанаманың бар болуымен бара бар. Бұл жағдайда,
жанаманың бұрыштық коэффициентi
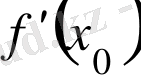 -қа тең. Туындының геометриялық мағынасы осы болады.
-қа тең. Туындының геометриялық мағынасы осы болады.
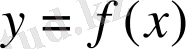 функциясы графигiне
функциясы графигiне
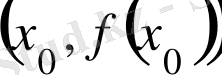 нүктесiнде жүргiзiлген
жанаманың теңдеуi
нүктесiнде жүргiзiлген
жанаманың теңдеуi
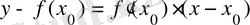
болады. Ал,
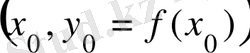 нүктесiнен жанамаға перпендикуляр болып өтетiн түзудi
нүктесiнен жанамаға перпендикуляр болып өтетiн түзудi
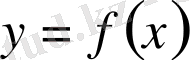 функциясы графигiне, осы нүктеде жүргiзiлген
нормаль теңдеуі
деп атайды, оның теңдеуi
функциясы графигiне, осы нүктеде жүргiзiлген
нормаль теңдеуі
деп атайды, оның теңдеуi
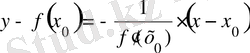 болады.
болады.
Егер материалдық нүктенiң қозғалыс заңы
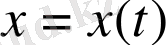 функциясы арқылы берiлсе, онда оның уақыт бойынша алынған туындысы жылдамдықты, ал екiншi реттi туындысы үдеудi анықтайды. Бұл бiрiншi реттi және екiншi реттi туындының механикалық мағынасы болып табылады.
функциясы арқылы берiлсе, онда оның уақыт бойынша алынған туындысы жылдамдықты, ал екiншi реттi туындысы үдеудi анықтайды. Бұл бiрiншi реттi және екiншi реттi туындының механикалық мағынасы болып табылады.
Мысал
.
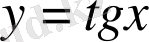 қисығына абсциссасы
қисығына абсциссасы
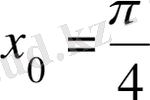 болатын нүктеде жүргiзiлген жанама және нормаль теңдеулерiн жазайық.
болатын нүктеде жүргiзiлген жанама және нормаль теңдеулерiн жазайық.
Шешуi: Нүктенiң ординатасын табамыз
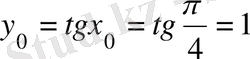 .
.
Келесі кезекте руындысын анықаймыз:
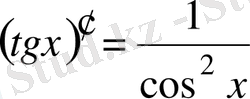 ; Сонда жанаманың бұрыштық коэффициентi
; Сонда жанаманың бұрыштық коэффициентi
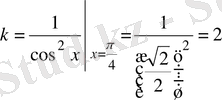 -ге тең болады.
-ге тең болады.
Сондықтан, жанама теңдеуi
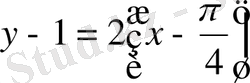 , нормаль теңдеуi
, нормаль теңдеуi
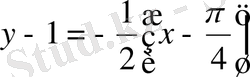 тең болады.
тең болады.
Дифференциал.
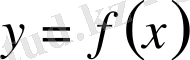 функциясының
х
0
нүктесiндегi өсiмшесiн
функциясының
х
0
нүктесiндегi өсiмшесiн
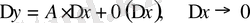 түрде өрнектеу мүмкiн болса, онда функцияны сол нүктеде дифференциалданады дейдi. Бұл өсiмшенiң
түрде өрнектеу мүмкiн болса, онда функцияны сол нүктеде дифференциалданады дейдi. Бұл өсiмшенiң
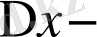 ке салыстырғандағы сызықтық бөлiгiн, яғни
ке салыстырғандағы сызықтық бөлiгiн, яғни
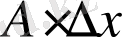 шамасын
шамасын
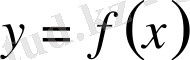 функциясының дифференциалы деп атайды да, оны
dy
символымен белгiлейдi:
функциясының дифференциалы деп атайды да, оны
dy
символымен белгiлейдi:
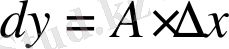 .
.
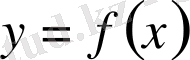 функциясының
х
0
нүктесiнде
функциясының
х
0
нүктесiнде
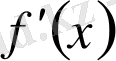 туындысы бар болып және
туындысы бар болып және
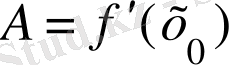 теңдiгiнiң орындалуы, функцияның берiлген нүктеде қажеттi және жеткiлiктi шарты болады.
теңдiгiнiң орындалуы, функцияның берiлген нүктеде қажеттi және жеткiлiктi шарты болады.
Сонымен, осы функция дифференциалы
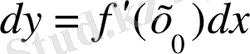 осы түрде өрнетеледі. Функциядағы
dy
дифференциалы бірінші ретті дифференциал, болмаса бірінші дифференциал деп аталады. Бірінші ретті дифференциалдан алынған дифференциалды
осы түрде өрнетеледі. Функциядағы
dy
дифференциалы бірінші ретті дифференциал, болмаса бірінші дифференциал деп аталады. Бірінші ретті дифференциалдан алынған дифференциалды
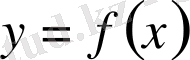 функциясының
х
0
нүктесіндегі екінші ретті дифференциалы(туындысы) деп, айтады, оны
функциясының
х
0
нүктесіндегі екінші ретті дифференциалы(туындысы) деп, айтады, оны
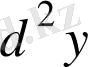 символымен белгiлейдi. Жалпы жағдайда, функцияның n-шi реттi дифференциалы деп, оның (n−1) реттi дифференциалынан алынған дифференциалды айтады, оны
символымен белгiлейдi. Жалпы жағдайда, функцияның n-шi реттi дифференциалы деп, оның (n−1) реттi дифференциалынан алынған дифференциалды айтады, оны
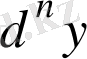 cимволымен белгiлейдi, бұл
cимволымен белгiлейдi, бұл
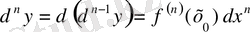
болады.
Мысал.
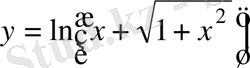 берілген функцияның бірінші және екінші ретті дифференциалдарын табу қажет.
берілген функцияның бірінші және екінші ретті дифференциалдарын табу қажет.
Шешуi:
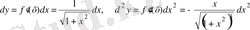
Осындай нәтиже алуға болады.
Лопиталь-Бернулли ережесi.
Лопиталь-Бернулли ережесi деп, туынды(дифференциал) көмегiмен
 және
және
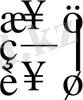 түрiндегi анықталмағандықты шешу әдісін айтамыз.
түрiндегi анықталмағандықты шешу әдісін айтамыз.
Теорема.
Егер
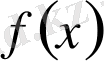 және
және
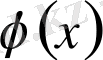 функциялары мынадай шарттарды қанағаттандырса: 1)
функциялары мынадай шарттарды қанағаттандырса: 1)
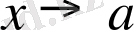 да шексiз аз немесе шексiз үлкен; 2)
да шексiз аз немесе шексiз үлкен; 2)
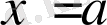 нүктесiнiң U
нүктесiнiң U
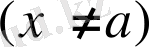 төңiрегiнде дифференциалданатын; 3)
төңiрегiнде дифференциалданатын; 3)
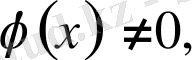
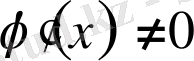 ,
,
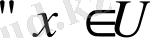 ; 4) егер
; 4) егер
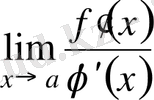 бар болса, онда
бар болса, онда
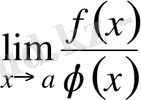 шегi бар болады және
шегi бар болады және
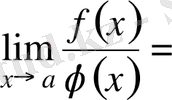
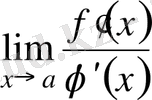
теңдiгi орындалады.
 болған кезде де, осы ережені пайдаланып есептерді орындауға болады. Тіпті, кейде Лопиталь ережесін бірнеше қайтара пайдалауға тура келеді.
болған кезде де, осы ережені пайдаланып есептерді орындауға болады. Тіпті, кейде Лопиталь ережесін бірнеше қайтара пайдалауға тура келеді.
Лопиталь ережесiн қайталап қолдану кезiнде, алдынғы қолдануда пайда болған туындылардың қатынасын әр түрлi жолдармен ықшамдап, ортақ көбейткiштерге қысқартып, бұрыннан белгiлi шектердi пайдаланған жөн (бiрақ, нәтижесiнде пайда болған өрнектi
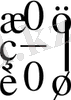 немесе
немесе
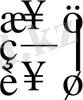 түрiндегi анықталмағандықты беретiндей түрде жазуды ұмытпау керек.
түрiндегi анықталмағандықты беретiндей түрде жазуды ұмытпау керек.
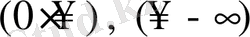 түрiндегi анықталмағандықты ашу үшiн, оларды түрлендiрiп
түрiндегi анықталмағандықты ашу үшiн, оларды түрлендiрiп
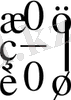 немесе
немесе
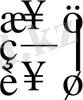 түрiндегi анықталмағандыққа келтiрiп, жоғарыдағы айтылған ереженi қолданады.
түрiндегi анықталмағандыққа келтiрiп, жоғарыдағы айтылған ереженi қолданады.
 түрiндегi анықталмағандықтарды
түрiндегi анықталмағандықтарды
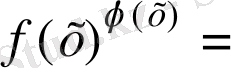
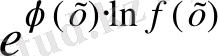 ,
,
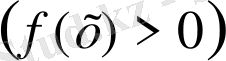
 түрлендiруi арқылы (
түрлендiруi арқылы (
 ) түрiндегi анықталмағандыққа, одан соң
) түрiндегi анықталмағандыққа, одан соң
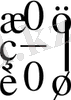 немесе
немесе
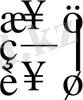 түрiндегi анықталмағандықтарға келтiрiп, оған Лопиталь ережесiн қолданады.
түрiндегi анықталмағандықтарға келтiрiп, оған Лопиталь ережесiн қолданады.
Мысал-1.
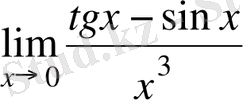 табу қажет.
табу қажет.
Шешімі:
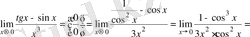

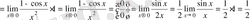 .
.
Есепті шешу барысында
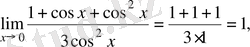
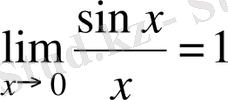
Біз шектерді пайдалып есептедік .
Мысал-2.
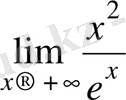 шегін табу қажет.
шегін табу қажет.
Шешімі: Есептi шешу үшiн Лопиталь ережесiн екi қайтара пайдаланамыз.
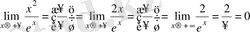 .
.
3. Мектепте интеграл тақырыбын тереңдетіп оқытудың әдістемесі.
3. 1 Интегралдың шығу тарихы
Дифференциалды және интегралды есептеулердің түрлі шешу тәсілдері көптеген жағдайда функциялардың нүктеделердегі шегіне тәуелді болып табылады.
Математика ғылымында ең бірінші дифференциал және интеграл терминдері анықталғаны, кейін келе бұл терминдерді жалпылау нәтижесінен «функцияның шегі» деп аталатын термин пайда болған.
Математика оқулықтарында интеграл терминін түрлі нұсқаларда тексеруден өткізіп, енгізген. Орыс және кеңес математигі, Колмогоров Андрей Николаевичтің оқулығының бастапқы шығарылымдарында интеграл Ньютон - Лейбництің формуласымен шығарылады. Ал, келесі шығарылымдарда интегралды есептеуді дәстүрлі әдіспен, яғни «интегралдық қосындының шегі» деп алып қарастырған. Осы секілді есептерді шешу әдістерін іздеу және шешіміндерін табу барысында Ньютон-Лейбницке дейін де, неміс математигі -Иоганн Кеплер, итальян математигі - Галилео Галилей, француз математигі - Блез Паскаль, ағылшын математигі - Джон Валлис, итальян математигі - Бонавентура Кавальери, фразцуз математигі - Рене Декарт және тағы басқа да ғалымдар мен ойшылдар көптеген еңбектер жазып, ғылымға өз үлесін қосқан.
1675 жылы неміс математигі - Готфрид Лейбниц енгізіп кеткен. Осы символ латынның Summa сөзінің алғашқы әріпімен белгіленіп, өзгертілген. Интеграл деген сөзді 1690 жылы швейцариялық физик, математик - Якоб Бернулли ойлап тапқан. Интеграл сөзі латынның «integro» сөзінен шыққан, «қалпына келтіру», «баяғы орнына түсіру» деген мағынаны білдіреді.
Швейцариялық математик Иоганн Бернулли мен неміс математигі - Готфрид Лейбниц әрқашан хабар алысып отырған. Сол арқылы швейцариялық физик, математик - Якоб Бернуллидің ұсынысын талқылап, келісім берген. Келісілген 1696 жылы математика ғылымының жаңа тараулары ашылған. Ол тараудыңатауы - Интегралдық есептеулер деп аталды. Бұл терминді Иоганн Бернулли тарихқа енгізді.
Интегралдық есептеулерге байланысты өзге ұғымдар кейінірек ғылымға ене бастады. Қарапайым функция атауын, қазіргі таңда ғылыми атау мен мағынаға ие «алғашқы функция» сөзі алмастырды. Бұл ұғымды 1797 жылы француз математигі Жозеф Луи Лагранж математика ғылымының тарихына алып келді. Латын тілінен «primitivus» сөзі аударылғанда «алғашқы, бастапқы» деген мағынаны білдіреді.
Қазіргі таңда математика ғылымында функциясы үшін жалпы алғашқы функцияларының жиыны «анықталмаған интеграл» деген ұғыммен аталады. Осы терминді анықтап көрсеткен неміс математигі - Готфрид Лейбниц болды. Неміс математигі барлық алғашқы функциялардың айырмашылығы біздің қалағанымызша алынған тұрақты сан ғана екенін енгізіп кетті.
Ал, математика ғылымына «анықталған интеграл» ұғымын енгізіп, мәңгілік тарихқа енгізген француз математигі Жан-Батист Жозеф Фурье еді.
Алайда интеграл шектерін Леонард Эйлер анықтаған.
Интеграл арқылы жазық фигуралардың (бейне) аудандары мен денелердің көлемдерін есептеу әдісі математика ғылымында айрықша орынға ие. Бұл есептеу әдісі Ежелгі грек математиктерінің «тауысу» әдісімен байланысты. Бұл терминді енгізуге ұсыныс тастаған ежелгі грек математигі -Книддік Евдокс. Осы әдіс-тәсілдің арқасында Квиддік Евдокс, екі шеңбердің аудандарының қатынасының осы шеңбердің диаметрлерінің квадраттарының қатынасына тең екенін дәлелдеген.
Алайда, бұл әдісті грек ғалымы, математигі Архимед жетілдірген. Геометрия ғылымының бір тарауында енген шеңбер ауданының формуласы грек математигі Архимедтің ойымен негізделген.
XVII ғасырда ғұмыр кешкен кемеңгер, ойшыл математиктердің көбісі керемет нәтижелерге қол жеткізгенімен, нақты есептеудің өзі табылмаған еді.
Негізгі дифференциалдық және интегралдық амалдардың арасындағы байланыс табылмағанеді. Бұл жалпылама алгоритмді анықтаған Ньютон және Лейбниц ғалымдары еді. Бұл заң Ньютон-Лейбниц формуласы деп ғылымға енді.
3. 2 Алғашқы функция мен интегралды оқыту әдiстемесi
Алғашқы функция ұғымының әдістемелік үлгісі төмендегідей:
- Бір-біріне кері амалдарға мысалдар келтіру.
- Интегралды дифференциал ұғымдарына кері амал деп қарастыру, ал алғашқы функция ұғымын интегралдау ұғымының нәтижесі деп енгізу.
- Алғашқы функцияға байланысты есептер шешу.
- Алғашқы функция ұғымының жалпы қасиеттерін білім алушыларға үйрету.
- Алғашқы функция ұғымдарының кестесін құрастыру.
- Алғашқы функция ережелерін пайдаланып есептер шешу.
Интеграл ұғымының әдістемелік үлгісі төмендегідей:
- Интеграл ұғымына байланысты есептер қарастыру.
- Интеграл терминінің анықтамасына тұжырым жасау.
4. Анықталмаған интеграл. Қисықсызықты трапецияның ауданы
Анықтама. Егер Х аралығында
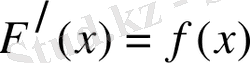 орындалса, онда F(x) функциясы
орындалса, онда F(x) функциясы
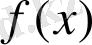 - тің алғашқы функциясы деп аталады.
- тің алғашқы функциясы деп аталады.
Теорема. Егер F(x) функциясы
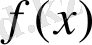 функциясының алғашқы функциясы болса, онда
функциясының алғашқы функциясы болса, онда
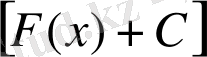 да
да
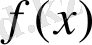 функциясының алғашқы функциясы болады.
функциясының алғашқы функциясы болады.
Дәлелдеу:
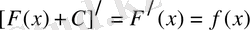
Анықтама. Х аралығындағы
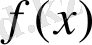 функциясының барлық алғашқы функциялары анықталмаған интеграл деп аталады және былай белгіленеді:
функциясының барлық алғашқы функциялары анықталмаған интеграл деп аталады және былай белгіленеді:
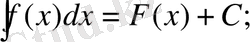
мұндағы
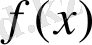 -интеграл астындағы функция,
-интеграл астындағы функция,
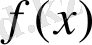 dx-интеграл астындағы өрнек,
dx-интеграл астындағы өрнек,
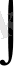 -интеграл белгісі, F(x) -алғашқы функция, С-кез-келген тұрақты делінеді.
-интеграл белгісі, F(x) -алғашқы функция, С-кез-келген тұрақты делінеді.
Анықталмаған интегралдың қасиеттері
1) Анықталмаған интегралдан алынған туынды интеграл астындағы функцияға тең:
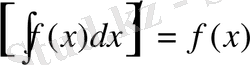
Дәлелдеу:
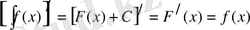
2) Анықталмаған интегралдан алынған дифференциал интеграл астындағы өрнекке тең:
Дәлелдеу:
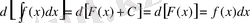
3) Функцияның дифференциалынан алынған интеграл сол функция мен кез-келген тұрақтының қосындысына тең:
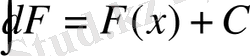
Дәлелдеу:
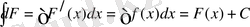
4) Тұрақтыны интеграл сыртына шығаруға болады:
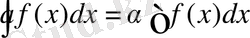
Дәлелдеу:
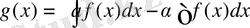
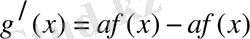
5) Функциялардың қосындысынан (айырымынан) алынған интеграл сол функциялардан алынған интегралдардың қосындысына (айырымына) тең:
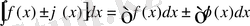
Элементар функциялардың интегралдары
1)
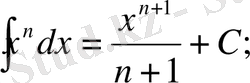
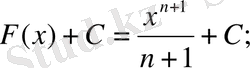
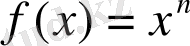
Дәлелдеу:
1-ші қасиет бойынша
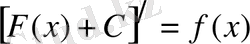
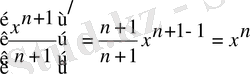 , демек
, демек
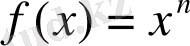 болғанда (1) орындалады.
болғанда (1) орындалады.
2)
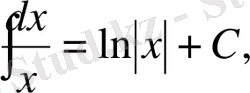
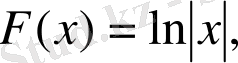
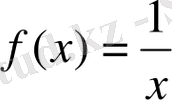
Дәлелдеу:
1-ші қасиет бойынша
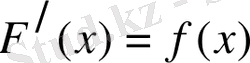
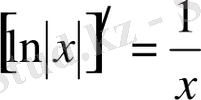 демек
демек
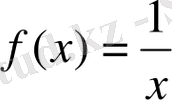 болады.
болады.
3)
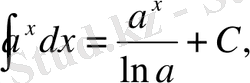
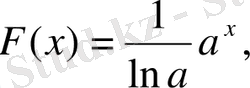
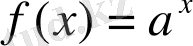
Дәлелдеу:
1-ші қасиет бойынша
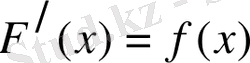
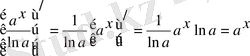
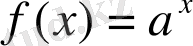
4)
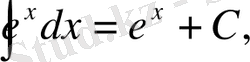
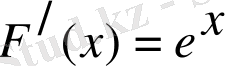
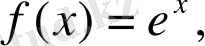 1-ші қасиет бойынша
1-ші қасиет бойынша
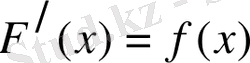 ,
,
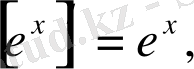
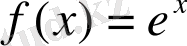
5)
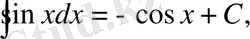
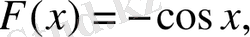
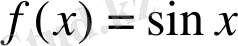 1-ші қасиет бойынша
1-ші қасиет бойынша
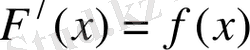
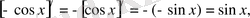
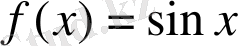
6)
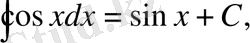
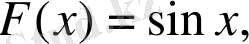
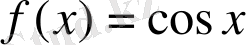 1-ші қасиет бойынша
1-ші қасиет бойынша
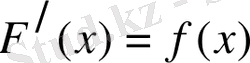
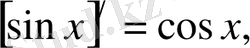
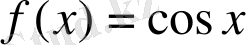
7)
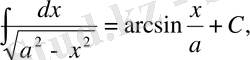
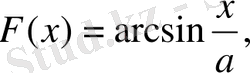
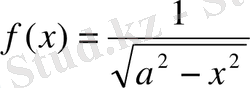 1-ші қасиет бойынша
1-ші қасиет бойынша
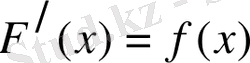 ,
,
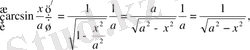
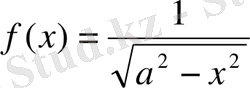
8)
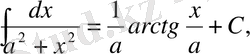
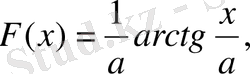
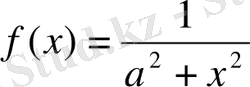 1-ші қасиет бойынша
1-ші қасиет бойынша
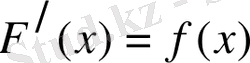 ,
,
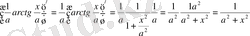 ,
,
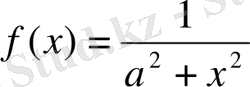
9)
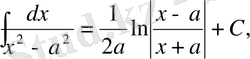
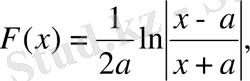
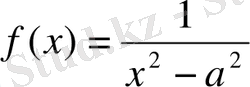 1-ші қасиет бойынша
1-ші қасиет бойынша
 ,
,
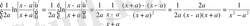 ,
,
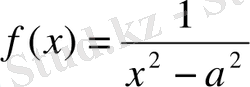
10)
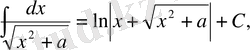
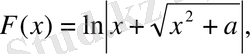
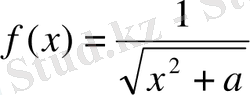 1-ші қасиет бойынша
1-ші қасиет бойынша
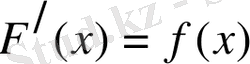 ,
,

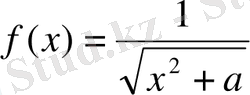
Анықталмаған интегралдар кестесі
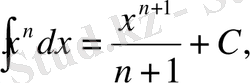
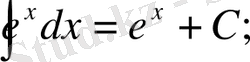
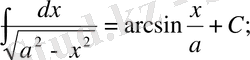
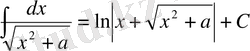
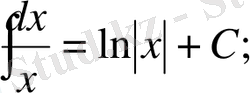
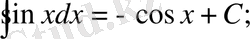
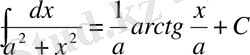
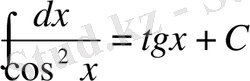
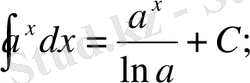
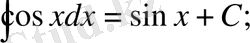
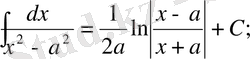
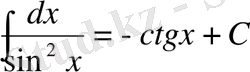
Математика пәні тәжірибесінде бір қабырғасы қисық сызықты бейнелердің(фигура) ауданып есептеуге байланысты сұрақтар да кездесіп отырады. Ал осындай фигураларды біз аранйы формулалармен есептей алмаймыз. Есептеу мүмкін емес. Сондықтан біз өзге тәсілді пайдалана отырып, есептер шығарамыз.
Қисықсызықты трапеция дегеніміз - жоғарыдан үзіліссіз, y=f(x) (f(x) >0) функциясының графигімен, бүйір жақтарынан x=a, x=b және астынан y=0 түзулерімен шектелген жазық фигураны атайды. Мұндағы абсцисса осінің кесіндісін - қисықсызықты трапецияның табаны дейді.
Қисықсызықты трапецияның ауданын есептеу барысында келесі алгоритмді пайдаланамыз:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz