Дифференциалдық теңдеулерді сандық әдістермен шығару

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

Ф.7.04-01

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М.ӘУЕЗОВ атындағы ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

Жаратылыстану ғылымдары және педагогикасы жоғары мектебі

Математика кафедрасы

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Дифференциалдық теңдеулерді сандық әдістермен шығару
Пәні: ___________________________________ ________________________
Мамандығы:5В010900 - Математика
Орындаған:Жұмаберді Жансая Группа:ЕП-17-1кт

Жетекші:Алибекова Жазира Даулетхановна

Жұмыс _______________ бағасына қорғалды
_____ ________ 2020ж
Норма бақылау:
_________________

Комиссия
_________________

_________________

Шымкент 2020 ж.
Ф.7.04-03

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М.ӘУЕЗОВ атындағы ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

Математика кафедрасы

Бекітемін

Каф. меңгерушісі

___________ Аширбаев Н.К.

________________2020ж.

№____Тапсырма
_Комплекс_талдау___________________ пәні бойынша курстық жұмыс
Студент Жұмаберді Жансая Топ ЕП-17-1кт
Жұмыс тақырыбы: Дифференциалдық теңдеулерді сандық әдістермен шығару
Берілген мәліметтер: Дифференциалдық теңдеулер, сызықтық дифференциалдық теңдеу, біртекті дифференциалдық теңдеу, дифференциалдық теңдеуді шешудің сандық әдістері.

№
Түсіндірме жазбасының мазмұны
(курстық жұмыс)
Беттер саны
Орындалу мерзімі
1
Кіріспе
~ 2

2
Негізгі бөлім
~10-15

3
Қорытыды
~ 1

4
Пайдаланылған әдебиеттер тізімі
~ 2

5
Жалпы
15-20

Ұсынылған әдебиеттер:
1___________________________________ _____________________________
2___________________________________ _____________________________
3___________________________________ _____________________________
Тапсырма берілген күні ___________________________________ __________
Жұмысты қорғау күні: 02.06.2020ж
Жұмыс жетекшісі: Алибекова Жазира Даулетхановна.
Тапсырманы орындауға қабылдаған ___________________________________ ___________________
Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
4
1 Дифференциалдық теңдеу ұғымы ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ..
5
1.1 Дифференциалдық теңдеулердің негізгі ұғымдары мен элементтері..
6
1.2 Сызықтық дифференциалдық теңдеу ... ... ... ... ... ... ... . ... ... ... ... ... ...
8
2 Дифференциалдық теңдеулерді сандық әдістер көмегімен жуықтап шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
9
2.1 Эйлер әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
10
2.2 Рунге-Кутта әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
12
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
23
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ...
24

Кіріспе
Жұмыстың өзектілігі. Дифференциалдық теңдеулердің шешімі барлық кезде элементар немесе арнаулы функциялар арқылы өрнектеле бермейтіні белгілі. Мысалы, сырттай қарағанда қарапайым 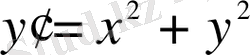көрінетін теңдеуінің шешімі элементар функциялар көмегімен жазылмайды. Көп жағдайларда дифференциалдық теңдеулер белгісіз функция бойынша сызықты емес күрделі түрдегі тәуелділікте болады. Ол тәуелділік кей жағдайда эксперименттік есептеулердің белгілі бір кестесі арқылы берілуі мүмкін. Бұл жағдайларда есепті шешудің үйреншікті әдістері не іске аспауы, не мерзімнен тысқары уақыт алатын есептеулерге әкеп тіреуі мүмкін. Сондықтан ол есептердің сандық сипаттамаларын жеткілікті дәлдікпен анықтайтын әдістерді табудың маңызы зор. Осындай әдістердін ішіндегі тиімдірегі -- сандык әдістері.
Дифференциалдық тендеуді сандық әдіспен жуықтап шешкенде, оның шешімі өзінін анықталу аралығында жататын нүктелердегі мәндері арқылы анықталады. Яғни жуыкталған шешім аналитикалық түрде (функциялық формула түрінде) емес сандар кестесі түрінде табылады. Әдетте жуықтап есептеу әдісін қолданып шығаратын есептің шешімі бар және жалғыз деп саналады.
Зерттеу жұмысының жаңалығы: Дифференциалдық теңдеулерді сандық әдістер көмегімен шығару әдістеріне салыстырмалы талдау.
Зерттеу жұмыстың практикалық құндылығы: дифференциалдық теңдеулерді сандық әдістерді пайдаланып шешуді оқытуды жетілдіру үшін зертханалық сабақтарда пайдалануға болатындығында.
Дипломдық жұмыстың мақсаты: Дифференциалдық теңдеулерді жуықтап шешу әдістерін талдап көрсету.
Зерттеу жұмысының міндеттері:
- Дифференциалдық теңдеулер және оның түрлері мен оларды шешу әдістерін оқып-үйрену және жүйелеу;
- Дифференциалдық теңдеулердің теориялық негізін оқып-үйрену;
- Дифференциалдық теңдеулерді шығаруда қолданылатын жуықтап есептеу әдістері мен оларды есептер шығаруда пайдалану мүмкіндіктерін көрсету;
Зерттеудің ғылыми нысаны: дифференциалдық теңдеулерді сандық әдістер көмегімен жуықтап шешу әдістері
Зерттеу жұмыстың әдіснамалық негіздері: сандық әдістер, математика пәндерін оқытудың теориясы мен әдістемесі.

1 Дифференциалдық теңдеу ұғымы
1.1 Дифференциалдық теңдеулердің негізгі ұғымдары мен элементтері

Дифференциалдық теңдеу деп ізделінді функцияны, оның туындылары мен дифференциалдарын және аргументтерін байланыстыратын теңдеуді айтамыз.
Теңдеуге кіретін туындының (дифференциалдың) ең жоғарғы реті дифференциалдық теңдеудің реті деп аталады.
Дифференциалдық теңдеудің шешімі деп кез келген функцияны айтамыз, егер оның өзін, туындысын және дифференциалын теңдеуге қойғанда тепе-теңдік шығатын болса.
Тек қана бір айнымалыға (бірнеше айнымалыға) тәуелді дифференциалдық теңдеуді қарапайым (дербес туындылы) дифференциалдық теңдеулер деп айтамыз.
Айталғанға сай п - ші ретті жай дифференциалдық теңдеу жалпы түрде былай жазылады:
(1)
Мұндағы х - тәуелсіз айнымалы, у - ізделінді функция, ал 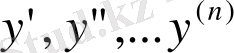-туындылар.
Егер (1) теңдеуде екі тәуелсіз айнымалыны 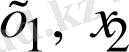бір ғана ізделінді функция 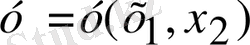болса, онда ол п - ші ретті дербес туындылы дифференциалдық теңдеу болар еді де, былай жазылар еді:

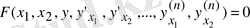
Егер (1) теңдеуде n=1 болса, онда алынған теңдеу
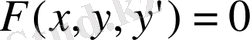(2)
бірінші ретті дифференциалдық теңдеу деп, ал қалған 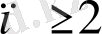болған жағдайларда жоғары ретті дифференциалдық теңдеу деп аталады.
Егер (2) теңдеу бойынша шешілетін болса, онда алынған теңдеу
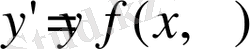(3)
туындысы бойынша шешілген бірінші ретті дифференциалдық теңдеу деп аталады. (3) теңдеудегі 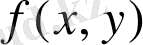функциясын кейінде берілген Д облысында бір мәнді, қос аргумент бойынша үздіксіз деп есептейміз. Д - облысы (3) теңдеудің анықталу облысы деп аталады.
Мысал 1.
а) 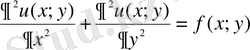- екінші ретті дербес туындылы дифференциалдық теңдеу;
б) 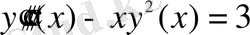- үшінші ретті қарапайым дифференциалдық теңдеу;
в) 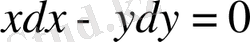- бірінші ретті қарапайым дифференциалдық теңдеу.
Коши теоремасы. Жалпы және дербес шешім
ші ретті айқын дифференциалдық теңдеу мына түрде жазылады:
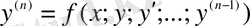, (6)
ал айқын емес ші ретті дифференциалдық теңдеу: .
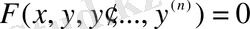Коши есебі. (3) дифференциалдық теңдеуінің, болғанда
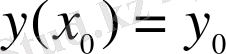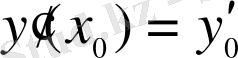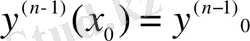,, ... , (7)
бастапқы шартын қанағаттандыратын шешімдерін тап.
Коши теоремасы. Егер қандай да бір тұйық облыста 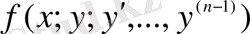функциясы барлық аргументі бойынша үзіліссіз болып және осы облыста оның дербес туындылары 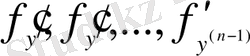табылса, онда (3) дифференциалдық теңдеуінің (4) бастапқы шартын қанағаттандыратын жалғыз шешімі болады, мұндағы 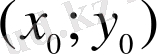нүктесі - осы облысқа тиісті нүкте.
Кез келген дифференциалданатын функция
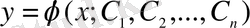, (8)
мұндағы 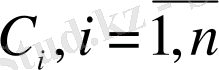- кез келген тұрақтылар, (5) дифференциалдық теңдеуінің жалпы шешімі деп аталады, егер:
а) ол 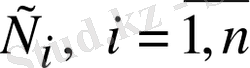-дің кез келген тұрақты мәндерінде (5) дифференциалдық теңдеуінің шешімі болса,
б) Коши теоремасының шартын қанағаттандыратын осы облыстың кез келген бастапқы шарты үшін,
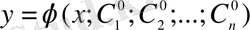(9)
шешімі бастапқы шартты қанағаттандыратындай 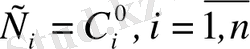тұрақтылары табылатын болса.
Дифференциал теңдеудің берілген облысындағы әрбір нүктесі үшін жалғыздық шарты орындалатын болса, онда (6) түріндегі шешім дербес шешім деп аталады.
(5) теңдеуінің айқын емес түрде берілген жалпы (дербес) шешімі:
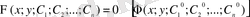сәйкесінше дифференциалдық теңдеудің жалпы (дербес) интегралы деп аталады. (5) теңдеуінің жалпы және дербес шешімінен басқа ерекше шешімдері болады.
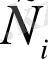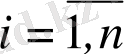-ді () қандай етіп таңдап алсақ та, жалпы шешімнен шықпайтын және шешімнің жалғыздық шарты бұзылатын нүктелерде орналасқан (облыстың шекарасында) шешімдерді ерекше шешімдер деп атаймыз.

1.1 Сызықтық дифференциалдық теңдеу

Егер дифференциал теңдеу ізделінді функция мен оның туындысы бойынша сызықты болса, ондай теңдеуді сызықты дифференциал теңдеу деп атаймыз.
Бірінші ретті сызықты дифференциал теңдеуді мына түрде жазуға болады:
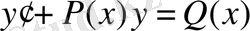(13)
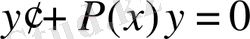, (14)
(13) - біртектес емес, ал (14) - біртектес дифференциал теңдеу деп аталады.
Біртектес дифференциал теңдеудің жалпы шешімін табалық:

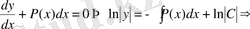
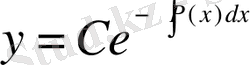(15)
Лагранж әдісін (тұрақты шаманы вариациалау әдісі) қолданып, (13) теңдеуінің шешімін алуға болады. Шешімді (15) түрінде іздейміз, мұндағы 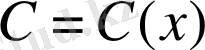- белгісіз функция. Онда (13) теңдеуіндегі 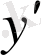-тың орнына:
,
ал 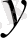- тің орнына (5)-ті қойсақ:

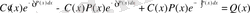
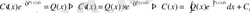
Осы табылған 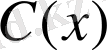-ті (5)-ке қоя отырып, (13) теңдеуінің жалпы шешімін аламыз.
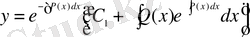(16)
Мысал 1. 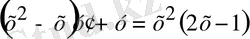теңдеуінің жалпы шешімін тап. Бастапқы шарт у(-2)=2 болғандағы, Коши есебін шеш.
Берілген теңдеуді екі жағын да 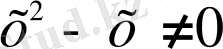өрнегіне бөліп келтіреміз:

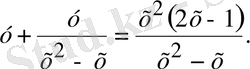
Мұнда

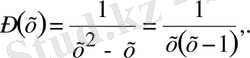
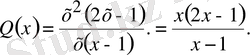
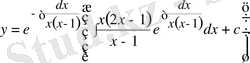Берілген теңдеудің (6) формуласына сәйкес жалпы шешімі:
(17)
Осы шешімнің ішіндегі интегралдарды шығаралық:

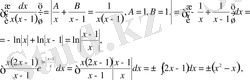
мұндағы 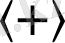және таңбалары 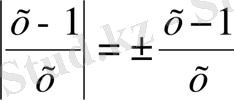теңдігінен шығады. Табылған интегралдарды (7) шешіміне қойсақ, берілген теңдеудің жалпы шешімін аламыз:
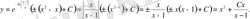у(-2)=2 бастапқы шартын қанағаттандыратын дербес шешімі:

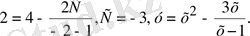
1.2 Біртекті дифференциалдық теңдеу

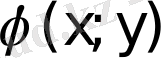функциясы 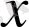пен 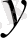бойынша -шы ретті біртекті функция деп аталады, егер кез келге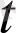н үшін: 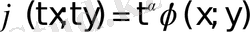теңдігі орындалатын болса.
Егер 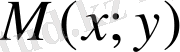және 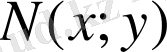- бірдей ретті біртекті функциялар болса, онда (1) теңдеуі біртекті дифференциалдық теңдеу деп аталады.
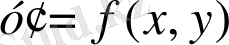теңдеуі біртекті болады, егер 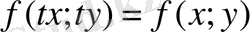, яғни, .
Біртекті дифференциалдық теңдеу айнымалыларды ауыстыру көмегімен айнымалылары ажыратылатын дифференциалдық теңдеуге келтіріледі: 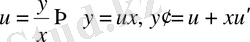немесе 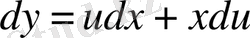. (19)
Мысал 1. Теңдеуді шеш: .
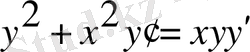Шешуі. Барлығын теңдеудің бір жағына жинақтау арқылы, біртекті дифференциалдық теңдеуге келтіреміз:

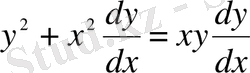
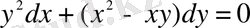
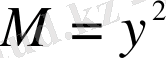және 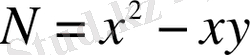- 2-ші ретті біртекті функциялар болғандықтан, теңдеу біртекті дифференциалдық теңдеу. 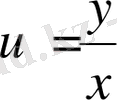белгілеуін енгіземіз.
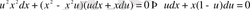- бұл айнымалылары ажыратылатын дифференциалдық теңдеу. Екі жағын да көбейтіндісіне бөліп, интегралдасақ:

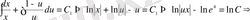
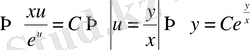- жалпы шешім.
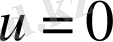және 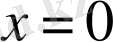жағдайлары 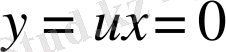жағдайымен тепе-тең. Жалпы шешімнен С=0 болғанда шығады.
2 Дифференциалдық теңдеулерді сандық әдістер көмегімен жуықтап шешу

Дифференциалдық теңдеу үшін Коши есебі. Жалпы ережелер
Бірінші ретті дифференциалдық теңдеу үшін Коши есебінің қойылуы. Айталық,
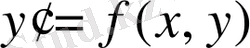(2.1)
бірінші ретті дифференциалдық теңдеуі және
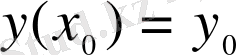(2.2)
бастапқы шарты берілсін. (2.1) теңдеуді және (2.2) бастапқы шартты қанағаттандыратын 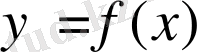функциясын табу керек.
(2.1) және (2.2) физикалық есебі егер материалдық нүкте қозғалысты (х0,у0) нүктесінде бастаса, осы материалдық нүктенің (2.1) теңдеуі бойынша жүру траекториясын табу болып табылады.
Егер (2.1) теңдеудегі 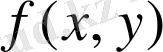функциясы айтарлықтай күрделі функция болатын болса, әдетте оны шешу үшін сандық әдістер қолданылады. Бұл әдістердің қасиетін былайша түсіндіруге болады: Коши есебінің шешімін табу қажет болатын (a,b) интервалы

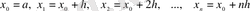
нүктелерімен жеткілікті көп бөлікке бөлінеді. Қандай да бір әдісті пайдаланып, белгісіз функцияның хі нүктелеріндегі мәндері табылады. Нәтижеде шешім кесте түрінде жазылады:

і
0
1
2
...
n-1
n
хі
х1
х2
х3
...
хn-1
хn
уі
у1
у2
у3
...
уn-1
уn
n-ші ретті дифференциалдық теңдеу үшін Коши есебі:
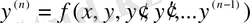(2.3)
теңдеуін және
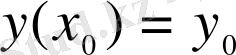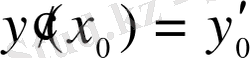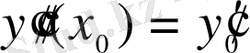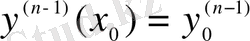, , , ..., (2.4)
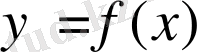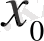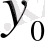
бастапқы шарттарын қанағаттандыратын функциясын табу болып табылады. Мұндағы , , 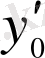, 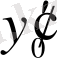..., 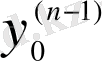берілген сандар.
Егер (2.3) теңдеудің жалпы шешімі табылса, онда Коши есебі тұрақтыларды табуға келтіріледі. алайда Коши есебінің жалпы шешімін табу сирек кездеседі, әдетте Коши есебін жуықтап шешуге тура келеді.
Шешімі табылатын формаға байланысты жуықтап шешу әдістерін екі топқа бөліп қарастыруға болады:
1. Аналитикалық әдістер. Бұл әдістер дифференциалдық теңдеудің жуық шешімін аналитикалық өрнек түрінде береді.
2. Сандық әдістер. Бұл әдістер жуық шешімді кесте түрінде береді[4].

2.1 Эйлер әдісі

Эйлер әдісі шешімді ізделінді y=f(x) функциясының жуық мәндерінің кестесі түрінде беретін сандық әдістер қатарына жатады.
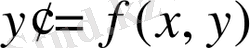(2.1.1)
дифференциалдық теңдеуін қарастырайық. Бастапқы шарты
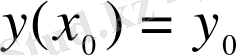(2.1.2)
Жеткілікті дәрежеде кіші һ қадамын таңдап алып, өзара тең ара қашықтықта орналасқан 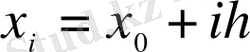(i=0,1,2,...) нүктелер жүйесін құрастырамыз.
Белгісіз y=f(x) функциясын x=x0 нүктесінің маңайында һ дәрежелері бойынша Тейлор қатарына жіктейміз:

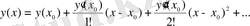
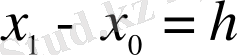қашықтығының жеткілікті дәрежеде кіші болатынын ескеріп, һ2, һ3, т.с.с. бар мүшелерді алып тастасақ, 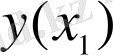үшін жуық

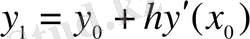
жуық формуласын аламыз. (1) теңдіктен 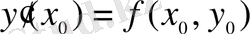екені белгілі. Сондықтан

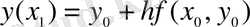
Дәл осы жолмен 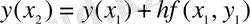аламыз. Және жалпы түрде Эйлер әдісінде 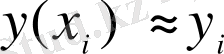жуық мәндері біртіндеп
, (i=0,1,2,...) (2.1.3)
формулалары арқылы есептеледі.
Сонымен қатар 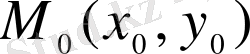нүктесі арқылы өтетін ізделінді y=у(x) интегралдық қисығы төбелері 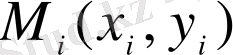, (i=0,1,2,...) нүктелерінде жататын 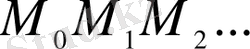сынық сызығымен алмастырылады; Эйлер сынығы деп аталатын осы сынықтың әрбір 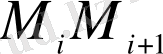буыны (2.1.1) теңдеудің Мі нүктесі арқылы өтетін интегралдық қисығының бағытымен бағыттас болады.
Егер (2.1.1) теңдеудің оң жағы қандай да бір тіктөртбұрышында
(N=const) (2.1.4)
(M=const) (2.1.5)
шарттарын қанағаттандаратын болса, онда қателікті келесідей бағалаймыз:
(2.1.6)
мұндағы - болғандағы дәл шешімнің мәні, ал n-ші қадамда алынған жуық мәні болып табылады.
(2.1.5) теңдеудің тек теориялық мағынасы бар. Тәжірибеде екілік қайта есептеу ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.