Функцияның кестелік тәсілмен берілуі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

Ф. 7. 04-01

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. ӘУЕЗОВ атындағы ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

$C:\Users\admin\Desktop\Лого ЮКГУ новый.jpg$

«Жаратылыстану ғылымдары және педагогикасы» жоғары мектебі

«Математика» кафедрасы

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Функцияны зерттеуге туынды қолдану әдістері.

Пәні:

Мамандығы:5В010900 - Математика

Орындаған:Өмеш Аружан Группа:ЕП-17-1кт

Жетекші:Абжапбаров Азимхан

Жұмыс бағасына қорғалды«» 2020жНорма бақылау:Комиссия:

Жұмыс бағасына қорғалды

«» 2020ж

Норма бақылау:

Комиссия

Шымкент 2020 ж.

Ф. 7. 04-03

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. ӘУЕЗОВ атындағы ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

«Математика» кафедрасы

Бекітемін

Бекітемін: Каф. меңгерушісі

Бекітемін: Аширбаев Н. К.

Бекітемін: «»2020ж.

№Тапсырма

пәні бойынша курстық жұмыс

Студент Өмеш Аружан Топ ЕП-17-1кт

Жұмыс тақырыбы Функцияны зерттеуге туынды қолдану әдістері.

Берілген мәліметтер: Функцияның берілу тәсілдері, тақ және жұп функциялар функцияның бірінші және екінші ретті туындылары арқылы зерттеу, функцияның экстремумы, функцияны зерттеудің және оның графигін құрудың жалпы тәртібі.

№

Түсіндірме жазбасының мазмұны

(курстық жұмыс)

Беттер саны

Орындалу мерзімі

№: 1

Түсіндірме жазбасының мазмұны(курстық жұмыс): Кіріспе

Беттер саны: ~ 2

Орындалу мерзімі:

№: 2

Түсіндірме жазбасының мазмұны(курстық жұмыс): Негізгі бөлім

Беттер саны: ~ 10-15

Орындалу мерзімі:

№: 3

Түсіндірме жазбасының мазмұны(курстық жұмыс): Қорытыды

Беттер саны: ~ 1

Орындалу мерзімі:

№: 4

Түсіндірме жазбасының мазмұны(курстық жұмыс): Пайдаланылған әдебиеттер тізімі

Беттер саны: ~ 2

Орындалу мерзімі:

№: 5

Түсіндірме жазбасының мазмұны(курстық жұмыс): Жалпы

Беттер саны: 15-20

Орындалу мерзімі:

Ұсынылған әдебиеттер:

Тапсырма берілген күні

Жұмысты қорғау күні: 02. 06. 2020ж

Жұмыс жетекшісі: Абжапбаров Азимхан.

Тапсырманы орындауға қабылдаған

Мазмұны

Кіріспе . . .

Функция ұғымы

Функцияның берілу тәсілдері . . . Функцияның кестелік тәсілмен берілуіФункцияның графиктік әдіспен берілуі . . . Функцияның аналитикалық тәсілмен берілуі
Жұп және тақ функциялар . . .
Функцияны бірінші және екінші ретті туындылар арқылы зерттеу.

4. Өспелі, кемімелі, кемімейтін, өспейтін және тұрақты болып келетін функциялардың белгілері. Туынды арқылы зерттеу

5. Функцияның экстремумы . . .

6. Функция графигінің дөңестігі мен ойыстығы.

7. Қисықтың асимптоталары. .

8. Функцияны зерттеудің және оның графигін құрудың жалпы тәртібі . . .

9. Қортынды . . .

10. Пайдаланған әдебиеттер . . .

Функцияны зерттеуге туынды қолдану әдістері.

Кіріспе

Мектеп математикасы курсындағы функция ұғымы негізгі ұғымдардың біріне жатады. Функциялық тәуелділік өмірдегі өзгерісті нақты және толық түрде кескіндеуге мүмкіндік береді, ол шамалар арасындағы өзара байланысты түсініп анықтауға үлкен септігін тигізеді.

Математикадағы негізгі ұғымның бірі функция болып саналады. Мектеп бағдарламасында бұл мәселеге көп көңіл бөлінген. Оқушылардың бұл ұғымды неғұрлым терең меңгеруі олардың математикалық білімдерінің деңгейінің анықтағышы іспеттес деуге де болады.

4-сынып математикасындағы айнымалысы бар өрнектерді оқып үйрену функцияны оқып үйренуге дайындық болып табылады. Функция ұғымының қазіргі математика мен оның қолданылуындағы ролі орасан зор. Белгілі функционалдық тәуелділіктерді инженерлер мен дәрігерлер, физиктер мен биологтар, агрономдар мен техниктер және т. с. с. пайдаланады.

Мектеп математикасының 5-сыныбында «функция» термині енгізілмейді, алайда осы ұғымды қалыптастыру жөнінде жыл бойы жүйелі түрде жұмыс жүргізіледі. Функция ұғымының қалыптасуына айнымалы шамалары бар арифметикалық есептерді шығару көмектеседі. 5 және 6 - сыныптарда функционалдық түсініктерді қалыптастыру жөнінде басталған жұмыс 7-сыныпта функция ұғымын енгізуге мүмкіндік береді. 7-сыныпта функция ұғымының мазмұны айқындалып, тиісті анықтама беріледі. Функцияның берілу тәсілдері (таблицалық, графиктік, аналитикалық) қарастырылады [1] .

у=kx және y=k/x функцияларын оқып -үйренеді. Олардың графиктері салынады. Сонымен қатар у=ах

\[\mathbf{\mathcal{D}}\]

пен у=ах

\[{\mathcal{L}}\,\]

функцияларының графиктерімен де танысады [2] .

Оқу материалының қысқаруы теориялық маңызы аса күштi нақтылы функцияларды оқып-үйренуге және олардың практикалық қолдануына көбiрек назар аударуына мүмкiндiк туғызды. Қазiргi кезде орта мектепте функция ұғымының мынадай анықтамасы қолданылады: "Егер айнымалы шама х -тiң әрбiр мәнiне белгiлi бiр заңдылық немесе ереже бойынша айнымалы шама у -тiң белгiлi бiр нақты мәнi сәйкес келсе, онда х айнымалысына байланысты өзгеретiн у айнымалысын функция деп атайды". Бұл анықтама алдын-ала күрделi ұғымдарды қарастыруды қажет етпейдi және ол функция ұғымының физикалық мағынасына өте жақын келедi.

Орта мектепте функцияны оқытудың әртүрлi тәсiлдерi алгебра курсының жалпы құрылымындағы функция тақырыбының алатын орнына да байланысты.

Функция ұғымын ертерек енгiзу (теңбе-тең түрлендiрулер мен теңдеулердi және теңсiздiктердi оқытудан алдын өту) функцияның қасиеттерiн дәлелдеу деңгейiне нұқсан келтiредi. Бұл мәселенiң қандай дәрежеде қойылуына байланысты, функцияны аналитикалық немесе көрнекi-геометриялық тәсiлмен анықтайды.

Функцияны оқыту әдiстемесiне оқушылардың нақты сандармен ертерек танысуы да белгiлi бiр дәрежеде әсер етедi. Мысалы, С. М. Никольский, М. К. Потапов, Н. Н. Решетникованың "6-сыныптағы алгебра" оқулығында [53] нақты сандар курстың ең басында қарастырылады. Бұл авторларға функцияны баяндау кезiнде үздiксiздiктiң қасиетiне де назар аударуға мүмкiндiк бердi. Осы авторлардың "7-сыныптағы алгебра" [54] оқулығында у=х ² функциясының графигi нелiктен үздiксiз қисық болатыны қарастырылған. Бұл кез келген терiс емес саннан квадрат түбiрдi графиктiк тәсiлмен анықтауға мүмкiндiк бердi.

8-сыныпта функция ұғымы енгізіліп, оған ғылыми түрде анықтама беріледі. Сызықтық функцияның графиктері қарастырылады. Функциялық түсініктер дамытылып отырады. Мысалы, бүтін теріс көрсеткіші бар дәрежелерді оқығанда у=ах

\[-1\]

, у=ах

\[-2\]

түріндегі функциялардың графиктері, квадрат түбірлерді оқығанда у=

\[{\sqrt{x}}\]

функциясының графигі, квадрат теңдеулерді оқығанда квадрат үшмүшеліктердің графиктері қарастырылады.

9-сыныпта оқылатын алгебра курсында функцияларды оқып-үйрену әрі қарай жалғастырылады. Берілген функцияға кері функция ұғымы енгізіледі, бұл у=

\[n{\sqrt{x}}\]

, y=lg x функцияларының қасиеттерін қарастырғанда пайдаланады. Көрсеткіштік функция, оның қасиеттері және оның графигі осы 9-сыныпта қарастырылады.

8-сынып геометриясында sin x пен cos x функцияларының қарапайым қасиеттері оқылады. tg x функциясы sin x /cos x қатынасы ретінде енгізіледі. Тригонометриялық функциялар негізінен 10-сыныпта оқылады.

10-11-сыныптарда «Алгебра және анализ бастамалары» курсында функция ұғымын және оның қасиеттерін, түрлерін, берілу тәсілдерін, графиктерін кеңінен қарастырады. Қарапайым түрлендірулерді қолданып, функцияның графиктерін салуды үйренеді. Функцияның нүктедегі шегі, функцияның нүктедегі және кесіндідегі үзіліссіздігі, олардың қасиеттері, функцияның туындысы ұғымымен танысады, туындыны функцияларды зерттеу кезінде қолдануды үйренеді. Алғашқы функция, анықталмаған және анықталған интеграл, қисықсызықты трапеция, n-ші дәрежелі түбір, рационал көрсеткішті дәреже, логарифм, көрсеткіштік және логарифмдік функциялар ұғымдары және осы ұғымның қасиеттерімен танысады. Иррационал теңдеулерді, көрсеткіштік, логарифмдік теңдеулер мен теңсіздіктер және олардың жүйелерін шешуді, сонымен қатар жазық фигуралардың ауданын интеграл арқылы табуды үйренеді.

Функция ұғымы

1. Функцияның берілу тәсілдері

Анықтама Егер бір белгілі ереже немесе заңдылық бойынша

\[X\]

жиынындағы

\[{\mathcal{N}}\]

-ң әрбір мәніне

\[\frac{\mathbf{\hat{J}}}{=}\]

жиынының тиянақты бір

\[\bigvee_{i}\sim\bigvee_{i}\]

мәні сәйкес келсе, онда

\[\bigvee_{i}\sim\bigvee_{i}\]

-ті

\[X\]

жиынында анықталған немесе берілген функция деп атайды және оны былай жазады:

\[y=f(x),\ \ \ \ y=\phi(x),\ \ y=g(x),\]

т. б. (1)

\[X\]

жиынында өзгеретін айнымалы

\[{\mathcal{N}}\]

-ті тәуелсіз айнымалы немесе функцияның аргументі деп ататйды,

\[Y=\{f(x)\}\]

жиынында өзгеретін айнымалы

\[\bigvee_{i}\sim\bigvee_{i}\]

-ті тәуелді айнымалы немесе функция деп атайды. Тәуелсіз айнымалы немесе аргумент

\[{\mathcal{N}}\]

өзгеретін

\[X\]

жиынын функцияның анықталу облысы деп атайды, ал тәуелді айнымалы немесе функция

\[\bigvee_{i}\sim\bigvee_{i}\]

өзгеретін

\[Y=\left\{f(x)\right\}\]

жиыны функция мәндерінің облысы деп аталады. Сонымен, функция, аргумент ұғымдары - өзімізді қоршап тұрған табиғаттың құбылыстарын зерттеудің нәтижесінде пайда болған ұғымдар.

Функциялар әр түрлі тәсілдер арқылы берілуі мүмкін. Біз функциялардың кестелік, графиктік және аналитикалқ тәсілдермен берілуіне тоқталамыз.

1. Функцияның кестелік тәсілмен берілуі Функция кестелік тәсілмен берілген жағдайда алдымен аргумент мәндері алынады да, сонан кейін әр аргументке сәйкес келетін функция мәндері анықталып, кесте құрылады.

\[y=x^{2}-1\]

функциясы үшін кесте құрамыз:

\[{\mathcal{N}}\]

\[X_{1}\]

\[X_{2}\]

\[X_{3}\]

. . .: . . .

\[\textstyle{\mathcal{X}}_{n-2}\]

\[{\mathcal{X}}_{n-1}\]

\[\textstyle{X_{n}}\]

\[f({\boldsymbol{x}})\]

\[f(x_{1})\]

\[f(x)_{2}\]

\[f(x_{3})\]

. . .: . . .

\[f(x_{n-2})\]

\[f(x_{n-1})\]

\[f(x_{n})\]

\[{\mathcal{N}}\]

-4: -4

-3: -3

-2: -2

-1: -1

0: 0

1: 1

2: 2

3: 3

4: 4

\[\bigvee_{i}\sim\bigvee_{i}\]

-4: 15

-3: 8

-2: 3

-1: 0

0: -1

1: 0

2: 3

3: 8

4: 15

Берілген аргументтердің мәндері бойынша функцияның мәндерін анықтау біздерге қиын есеп емес. Алгебра курсынан белгілі:

\[x{\hat{1}}\ {\stackrel{c}{\underset{\mathrm{G}}{6}}}{\overset{\underset{\mathrm{G}}{}}{\boldsymbol{\hat{1}}}}\]

жағдайы үшін

\[f(x)=\sin x,\ f(x)=\cos x\]

функцияларының мәндері кесте арқылы анықталған,

аралығында өзгергенде

\[f(x)=t g x\]

функциясының мәндері, ал

\[x{\hat{1}}\ {\frac{\alpha}{8}},{\frac{\alpha}{2}}{\hat{\mathbf{t}}}\]

үшін

\[f(x)=c t g x\]

функциясының мәндері кесте арқылы анықталған. Логарифмдік функцияның кестесі де функцияның кестелік тәсілмен берілуінің мысалы бола алады

\left\lbrack \mathbf{3} \right\rbrack

2 Функцияның графиктік әдіспен берілуі

Анықтама қос сандар жиынын

\[f({\boldsymbol{x}})\]

функциясының графигі деп атайды. Функцияның графигін координаттық жазықтыққа салады. Өзара перпендикуляр екі координаттық түзу және оларға ортақ

\[{\cal{O}}_{}^{}\]

координаттар басы орналасқан жазықтықты координаттар жазықтығы дейді. Горизонталь орналасқан түзуді абсциссалар осі деп атайды да,

\[X\]

-пен белгілейді, вертикаль орналасқан түзуді ординаталар осі деп атап,

\[\frac{\mathbf{\hat{J}}}{=}\]

арқылы белгілейді, ал олардың қиылысу нүктесін координаттар басы дейді, оны

\[{\cal{O}}_{}^{}\]

әрпімен белгілейді. Тәуелсіз айнымалы

\[{\mathcal{N}}\]

-ң мәндері абсциссалар осіне салынады. Ал

\[\bigvee_{i}\sim\bigvee_{i}\]

-ң мәндері ординаталар осінің бойына салынады.

\[\left\{(x,y):x\hat{\textbf{r}}\ R,\,y=f(x)\right\}\]

нүктелер жиыны берілсін.

\[{\cal O}y\]

осіне параллель түзулердің кез келгені осы нүктелер жиынын бір ғана нүктеде қиып өтетін болса, онда бұл нүктелер жиыны бір мәнді

\[y=f(x)\]

функциясын анықтайды.

Сонымен, абсциссалары - тәуелсіз айнымалы, ал ординаталары - функция мәндері болып келген

\[x O y\]

жазықтығындағы

\[\left\{(x,f(x))\right\}\]

нүктелер жиынын

\[y=f(x)\]

функциясының графигі деп атайды.

Бір мәнді

\[y=f(x)\]

функциясының графигі

\[x O y\]

жазықтығында орналасқан (функцияның анықталу облысына байланысты) біртұтас қисық. Анықталу облысының ішінде

\[{\cal O}y\]

осіне параллель жүргізілген түзулер қисықпен бір ғана нүктеде қиылысады .

3. Функцияның аналитикалық тәсілмен берілуі

Айнымалылар арасындағы сәйкестік формуламен берілсе, онда функция аналитикалық түрде берілді дейді. Төменде берілген функциялар аналитикалық тәсілге мысал бола алады:

1) Тура пропорционалдық тәуелділік -

\[y=k x\]

, мұнда

\[\overline{{K}}_{\mathrm{v}}\]

- тұрақты,

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

2) Кері пропорционалдық тәуелділік -

\[y={\frac{k}{x}},\ (k\neq0),\]

мұнда

\[\overline{{K}}_{\mathrm{v}}\]

- тұрақты,

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

3) Сызықтық функция -

\[y=k x+b\]

, мұнда

\[\overline{{K}}_{\mathrm{v}}\]

және

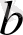- тұрақты сандар,

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

4) Көрсеткіштік функция -

\[y=a^{x},(a>0,a\ \neq1)\]

, мұнда

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

5) Логарифмдік функция -

\[y=\log_{a}x,(a>0,a\neq1)\]

, мұнда

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

6) Дәрежелік функция -

\[y=x^{a}\,,\]

мұнда

\[\langle f\rangle\]

- кез келген нақты сан,

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

7) Тригонометриялық функциялар -

\[y=\sin x,\ y=\cos x,\ y=t g x,\ y=c t g x\]

, мұнда

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

8) Кері тригонометриялық функциялар -

\[y=\arcsin x,y=\operatorname{arccos}x,y=a r c t g x,y=a r c c t g x\]

, мұнда

\[{\mathcal{N}}\]

- тәуелсіз айнымалы,

\[\bigvee_{i}\sim\bigvee_{i}\]

- тәуелді айнымалы.

Міне, осы функциялардың барлығы - аналитикалық тәсілмен беріліп тұрған функциялар. Осы функциялардың көптеген қасиеттерін білеміз. Анықталу облыстарын және мәндерінің өзгеру облыстарын анықтай аламыз. Графиктерін құра аламыз.

Енді функциялардың негізгі қасиеттеріне тоқталайық.

2. Жұп және тақ функциялар

Егер

\[X\]

жиынында оның кез келген

\[{\mathcal{N}}\]

элементімен қатар

\[{\underline{{\underline{{\mathcal{N}}}}}},{\mathcal{N}},\]

элементі де бар болса, онда бұл жиын симметриялы жиын деп аталады. Мысалы,

\[\left(-\theta,Q\right),\left[-\ 2,+2\right],\ \left(\neg{\overset{\bigtriangledown}{\Omega}}\ ,+\ \infty\right)\]

- симметриялы жиындар.

Анықтама Егер

\[y=f(x)\]

функциясының анықталу облысының кез келген

\[{\mathcal{N}}\]

үшін

\[f(\leftarrow x)=f(x)\]

теңдігі орындалса, онда ол жұп функция деп аталады.

Анықтама Егер

\[y=f(x)\]

функциясының анықталу облысының кез келген

\[{\mathcal{N}}\]

үшін

\[f(\leftarrow x)=-f(x)\]

теңдігі орындалса, онда ол тақ функция деп аталады.

Мысалы,

\[y=x^{2}\]

- жұп функция, себебі:

\[(\leftarrow x)^{2}=(\leftarrow x)\chi(\leftarrow x)=x^{2};\]

\[y=x^{3}\]

- тақ функция, себебі:

\[\left(-\chi\right)^{3}\,\ =-\chi^{3}\,.\]

Ал

\[f(x)=x^{2}+x^{5}\]

функциясы жұп функцияға да, тақ функцияға да жатпайды, себебі:

\[f(\cdot x)=(-\,x)^{2}+(-\,x)^{3}=x^{2}\cdot\ x^{3}\textbf{i}\frac{\mathbf{j}\,f(x),}{\left[\begin{array}{l}{f(x),}\\ {f(x)}\end{array}\right]}\]

Жұп функцияның графигі ордината осіне қарағанда симметриялы қисық болады. Тақ функцияның графигі бас нүктеге қарағанда симметриялы қисық болады.

3. Функцияны бірінші және екінші ретті туындылар арқылы зерттеу

Анықтама

\[X\]

жиынында өзгеретін

\[y=f(x)\]

функциясы берілсін.

\[{\boldsymbol{\Delta}}x\]

- аргумент өсімшесіне сәйкес анықталған функция өсімшесі (яғни

\[{\boldsymbol{\Delta}}x\]

өсімшесі

\[X\]

жиынына тиісті, таңбасына қарай, егер

\[\scriptstyle{\mathrm{pr}}\circ\scriptstyle0\]

болса,

\[(x+\Delta x)\]

нүктесі

\[{\mathcal{N}}\]

нүктесінің оң жағына, ал

\[\scriptstyle{\mathrm{pr}}\circ{\mathrm{o}}\]

болса, онда

\[(x+\Delta x)\]

нүктесі

\[{\mathcal{N}}\]

нүктесінің сол жағына орналасады) :

\[\mathrm{D}y=f(x+\mathrm{D}x)-f(x)\]

, (1)

мұндағы

\[\Delta y\]

- аргумент

\[{\mathcal{N}}\]

-ке

\[{\boldsymbol{\Delta}}x\]

өсімшесін бергенде

\[y=f(x)\]

функциясының қабылдаған өсімшесі. Енді функция өсімшесін аргумент өсімшесіне бөлеміз. Сонда:

\[{\frac{\mathrm{D}y}{\mathrm{D}x}}={\frac{f(x+\mathrm{D}x)-f(x)}{\Delta x}}\]

(2)

Осы теңдікте аргумент өсімшесі

\[{\boldsymbol{\Delta}}x\]

нөлге ұмтылғандағы шекке көшеміз:

\[\textstyle\mid_{\mathrm{Dreo}}\Pi{\underset{\mathrm{Dx}}{}}=\operatorname*{lim}_{\mathrm{Dx}\to0}{\frac{f(x+\mathrm{D}x)-f(x)}{\Delta x}}\]

. (3)

Егер осы айырымдық қатынастың

\[\scriptstyle{\mathrm{br}}\quad\quad\]

-да тиянақты шегі бар болса, онда оны

\[y=f(x)\]

функциясының

\[{\mathcal{N}}\]

нүктесіндегі туындысы деп атайды және оны былай белгілейді:

\[y{\phi}={f}^{\prime}(x)\]

немесе

\[{\frac{d y}{d x}}=f^{\prime}(x)\]

. (4)

Функцияның туындысын табуды функцияны дифференциалдау деп атайды.

Төменде элементар функциялардың, күрделі функциялардың туындыларының кестесі және дифференциалдар кестесі берілген. Бұл кестелерді функцияның туындысын есептеуде қолданамыз $\lbrack 3\rbrack$ .

Элементар функциялардың туындылар кестесі

1: 1

- тұрақты сан:

\[y=c,\ \ c\]

- тұрақты сан

\[\scriptstyle{9\neq0}\]

1: 2

- тұрақты сан:

\[y=\wedge^{a}\;,\;\ O\]

- кез келген нақты сан

\[y\phi=a\cdot x^{a-1}\]

1: 3

- тұрақты сан:

\[y=a^{x},\ \ a>0,\ a\ \neq1\]

\[y\phi=a^{x}\cdot\ln a\]

1: 4

- тұрақты сан:

\[y=e^{x},\ e\approx2.72\]

- иррационал сан

\[y\phi=e^{x}\]

1: 5

- тұрақты сан:

\[y=\log_{a}x,\,a>0,\,a\neq1\]

\[y\phi={\frac{1}{x\ln a}}\]

1: 6

- тұрақты сан:

\[y=\ln x,\,x>0\]

\[y\phi={\frac{1}{x}}\]

1: 7

- тұрақты сан:

\[y=\sin x\,\]

\[y\phi=c o s\;x\]

1: 8

- тұрақты сан:

\[y=\cos x\]

\[y\phi=-\sin\chi\]

1: 9

- тұрақты сан:

\[y=t g x\]

1: 10

- тұрақты сан:

\[y=c t g x\]

\[y\phi=-\ \frac{1}{\sin^{2}x},\ x^{1}\ \pi n,n\in Z\]

1: 11

- тұрақты сан:

\[y=\arcsin x\,\]

\[y\phi=\frac{1}{\sqrt{1-\ X^{2}}},\ \ x\hat{\imath}\ \ (-1;1)\]

1: 12

- тұрақты сан:

\[y=\operatorname{arcos}x\]

\[y\phi=-\ \frac{1}{\sqrt{1-\ x^{2}}},\ \,x\hat{1}\ \ (-1;\ 1)\]

1: 13

- тұрақты сан:

\[y=a x c g x\]

\[y\phi={\frac{1}{1+x^{2}}}\]

1: 14

- тұрақты сан:

\[y=a r c c t g x\]

\[y\phi={\frac{1}{1+x^{2}}}\]

Күрделі функциялардың туындылар кестесі

1: 1

- кез келген нақты сан:

\[y=\wedge^{a}\;,\;\ O\]

- кез келген нақты сан

\[y\phi=a\,\times x^{a-1}\times x^{\prime}\]

1: 2

- кез келген нақты сан:

\[y=a^{x},\ \ a>0,\ a\ \neq1\]

\[\forall\phi=a^{x}\dim a\times^{t}\]

1: 3

- кез келген нақты сан:

\[y=e^{x},\ e\approx2.72\]

- иррационал сан

\[y\phi=e^{x}\times x^{\prime}\]

1: 4

- кез келген нақты сан:

\[y=\log_{a}x,\,a>0,\,a\neq1\]

\[y\phi={\frac{1}{x\ln a}}\mathbf{x}^{\prime}\]

1: 5

- кез келген нақты сан:

\[y=\ln x,\,x>0\]

\[y\phi={\frac{1}{x}}\chi x^{\prime}\]

1: 6

- кез келген нақты сан:

\[y=\sin x\,\]

\[y\phi=\cos x\times x^{\prime}\]

1: 7

- кез келген нақты сан:

\[y=\cos x\]

\[y\phi=-\ \sin x\times x^{\prime}\]

1: 8

- кез келген нақты сан:

\[y=t g x\]

\[y\phi{\overset{1}{=}}~\!\!\!\underbrace{1}{\cos^{2}x}\times\!\!\!\star\forall x\!\ /\ x^{1}\ {\frac{p}{2}}+\pi n,\,n\in\!Z\]

1: 9

- кез келген нақты сан:

\[y=c t g x\]

\[y\phi=-\ \frac{1}{\mathrm{sin}^{2}\ x}\times\!x\backslash\chi\ ^{1}\ \pi n,\ n\in\mathbb{Z}\]

1: 10

- кез келген нақты сан:

\[y=\arcsin x\,\]

\[y\phi=\frac{1}{\sqrt{1-\ x^{2}}}\times\!x\chi\cdot\ x\hat{1}\ \left(-1;1\right)\]

1: 11

- кез келген нақты сан:

\[y=\operatorname{arcos}x\]

\[y\phi=-\ \frac{1}{\sqrt{1-\ x^{2}}}\Re x\forall\ \ x\hat{1}\ \left(-1;1\right)\]

1: 12

- кез келген нақты сан:

\[y=a r c g x\]

\[y\phi=\frac{1}{1+x^{2}}\times x^{\prime}\]

1: 13

- кез келген нақты сан:

\[y=a r c c t g x\]

\[y\phi=\frac{1}{1+x^{2}}\times x^{\prime}\]

Дифференциалдар кестесі

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

Ұқсас жұмыстар

Функцияның берілу тәсілдері

ФУНКЦИЯ. ШЕК. ҮЗДІКСІЗДІК

Функцияның нүктедегі шегі

Математика сабақтарында оқушылардың танымдық белсенділігін арттырудың жолдарын сипаттай отырып функция мәнін түсіндіру, оның ең үлкен және кіші амалдарын табу жолдарын зерттеу

Функция және оның графигі

Функцияның туындысы. Функцияны бірінші және екінші ретті туындылар арқылы зерттеу

Математикалық функциялар

Функция ұғымы. Жоғарғы ретті туындылар мен дифференциалдар

Функция және оның графигі. Функцияның берілу тәсілдері және оның графигі

Жиындар мен математикалық логика элементтері

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz