Қатты дененің бетіне жұқпайтын сұйықтың тамшысы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 31 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. Х. ДУЛАТИ АТЫНДАҒЫ ТАРАЗ ӨҢІРЛІК УНИВЕРСИТЕТІ

«Қорғауға жіберілді»

« » 2022ж

«Физика және ІТ» кафедрасының меңгерушісі Б. Тасуов

ДИПЛОМДЫҚ ЖОБА

Тақырыбы: «Ерітінділердің беттік керілу коэффиценттерінің температураға тәуелділігін тәжірибе жүзінде зерттеу әдісі»

5B011000 - «Физика» мамандығы бойынша

Орындағандар: Т. Ж. Оразымбекова, К. Т. Аширбаева, А. А. Қылышева

Ғылыми жетекшісі:

Ф-м. ғ. к, профессор Т. Бижігітов

Тараз 2022

Мазмұны

Кірспе . . .

Кірспе . . .: І-бөлім. Сұйықтардың серпімділік коэффициенттерін зерттеу әдістері . . .

3: 4

Кірспе . . .: 1. 1 Сұйықтардың беттік керлеу коэфициенттерін есептеу әдістері . . .

3: 4

Кірспе . . .: ІІ-бөлім Ерітінділердің беттік керілу коэффициенттерінің концентрация мен температураға тәуелділігін анықтау әдісі . . .

3: 24

Кірспе . . .: 2. 1 Беттік керілу коэффициентінің температураға тәуелділігін зерттейтін қондырғы . . .

3: 24

Кірспе . . .: Қорытынды . . .

3: 32

Кірспе . . .: Пайдаланылған әдебиеттер тізімі . . .

3: 33

Кіріспе

Қазіргі кезде ғалымдар сұйықтарға физикалық, химиялық, биологиялық әсерлер (қысым, температура, өрістер, концентрация т. б) жасау арқылы практикалық маңызы зор жетістіктерге жетуге болатындығын дәлелдеп отыр. Мысалы, сұйықтардың беттік керілуі, тұтқырлық коэффиценттерін сыртқы параметрлердің көмегімен өзгерту олардың денелерге жұғуы мен жұқпауын, сіңіуі мен сіңбеуі, ағыстардың жылдамдықтарын арттырып, кемітуге мүмкіндік туғызада. Яғни, мұнай өнімдерінің, ерітінділердің, жалпы сұйықтардың ағыстарын, басқа денелермен жанасқанда орын алатын құбылыстарды басқара аламыз.

Ұсынылып отырған ғылыми жобада этил спиртінің (С ₂ Н ₅ ОН), ас тұзының (NаCl), бензолдың (С ₆ Н ₆ ) сабын ерітінідісінің беттік керілу коэффиценттерінің екі рет дистилляцияланған судағы пайыздық концентрациясына және температураға тәуелділігін зерттейтін қондырғы жинастырылып

$\sigma = \sigma(\%), \sigma = \sigma(т)$ тәуелділік графиктері тұрғызылып, өлшеулер мен теориялық есептеулерден алынған нәтижелерге теориялық тұрғыдан түсініктемелер берілген. Жинастырылған қондырғылар жақсы зерттелген сұйықтарды зерттеу арқылы сынақтан өткізілген.

Зерттеудің мақсаты -этил спиртінің, ас тұзының, сабынның судағы ерітінділерінің беттік керілу коэффиценттеріне концентрация мен температураның әсерін зерттеу.

Проблеманың өзектілігі -зерттеліп отырған үлгілер адам баласының тұрмыстық жағдайында, медицинада, тамақ өнеркәсібінде жиі қолданатындықтан, оның физикалық, химиялық, биологиялық қасиеттерін зерттеудің теориялық және практикалық мәні үлкен.

Пәннің зерттелуі - бітірушіні студент кезінде молекулалық физика термодинамика, статистикалық физика, математикалық физика әдістері пәндерінен алған теориялық білімдерін практикада қолдана білуге дағдыландыру.

Зерттеудің ғылыми болжамы -зерттеліп отырған су ерітінділеріне концентрация мен температураның әсерін анықтап, оның қолданылатын жерлердегі сапалылығына болжамдар жасау

Зерттеудің міндеттері :

а. Тәжірибелік өлшеулермен теориялық есептеулер арқылы

$\sigma = \sigma(\%), \sigma = \sigma(\ t)$ тәуелділіктерін анықтау

ә. Кестелер мен тұрғызылған $\sigma = \sigma(\%), \sigma = \sigma(t)$ графиктеріне талдаулар жасау

б. Үлгілердің практикада қолдануларына болжамдар беру

Зерттеу әдістері:

Тәжірибелік өлшеулер жүзгізуді жоғары оқу-орындарында физикалық оқу зертқаналарында қолданылатын сұйықтардың беттік керілу коэффицентін сақинаны оның бетінен жұлу әдісін жетілдіру мақсатында іске асыру

Зерттеу базасы-Тараз қаласы, №7 мектеп гимназияцындағы, физика зертханасындағы қондырғы қолданылды.

І-бөлім. Сұйықтардың серпімділік коэффициенттерін зерттеу әдістері

1. 1 Сұйықтардың беттін керлеу коэфициенттерін есептеу әдістері

Сұйықтардың басқа ортамен жанасатын беттері оның басқа массаларымен салыстырғанда ерекше күйде болады. Өйткені, сұйықтардың шекарадағы қабаттарындағы молекулалар бір жағынан өзінің, екінші жағынан жанасатын денелердің молекулаларымен әсерлеседі. Сондықтан, шекарада орналасқан молекулаларға әсер ететін күштердің шамалары әртүрлі болғандықтан, олар тепе-теңдікте болмайды. Оған теңәсерлі күш сұйықтың ішіне немесе жанасатын денеге қарай бағытталады.

Сұйық өзінің қаныққан буымен шекаралас болса, онда беттік қабаттағы молекулаларға сұйықтың ішіне қарай бағытталған күш әсер әтеді. Бұл құбылыс сұйықтың тығыздығы, қаныққан буының тығыздығынан артық екендігімен түсіндіріледі. Яғни, беттік қабаттағы молекулаларға қаныққан буының молекулаларының әсерлесу күшінен сұйық молекулаларының әсерлесу күші артық. Демек, беттік қабаттан молекула сұйықтың ішіне қарай қозғалғанда оң, керісінше ішінен беттік қабатқа қозғалғанда теріс жұмыс атқарылады.

Сұйықтың беті керіліп ұлғайғанда қандай да бір молекулалар саны оның көлемінен бетіне ауысады. Ол үшін сыртқы жұмыс атқарылуы қажет. Демек, сұйықтың беті ұлғайғанда теріс, ал кемігенде оң жұмыс атқарылады. Қазіргі таңда әртүрлі сыртқы физикалық, химиялық параметрлердің сұйықтардың беттік қабатында болатын үдерістерге әсерін зерттеудің практикалық және теориялық маңызы үлкен. Сұйықтардың беттік керілу коэффиценттерін арттырып, кеміту арқылы біз капиллярлық құбылыстарға және жұғу, жұқпау, сіңу, сіңбеу үдерістеріне өзгерістер енгізе аламыз.

Молекулалардың арасында пайда болатын күштердің табиғаты ерекше. Өйткені, бұл күштер конденсацияланған ортаның пайда болуына және оның физикалық қасиеттеріне әсерін тигізеді. Молекулалық күштердің газ-сұйықтық, сұйықтық-қатты дене, газ-қатты дене шекараларындағы күштерді талқылайық. Сұйықтық беттік қабатында орналасқан молекулаға әсер ететін күшті қарастырайық. Қабаттың қалындығын молекулалық күштердің әсерлесу сферасының радиусына (шамамен 10 ^-7 см) тең деп есептейік. Егер сұйықтың ішінде орналасқан молекулаларының Ван-дер-Ваальс күштерінің теңәсерлі күші нөлге тең болса, беттік қабатта бұл күштің шамасы нөлге теңелмейді. Өйткені, қарастырып отырған жағдайда бетке перпендикуляр сұйықтың ішіне қарай бағытталған теңәсерлі күш туындайды (1. 1. 1 сызба) [1, 2, 3, 4] .

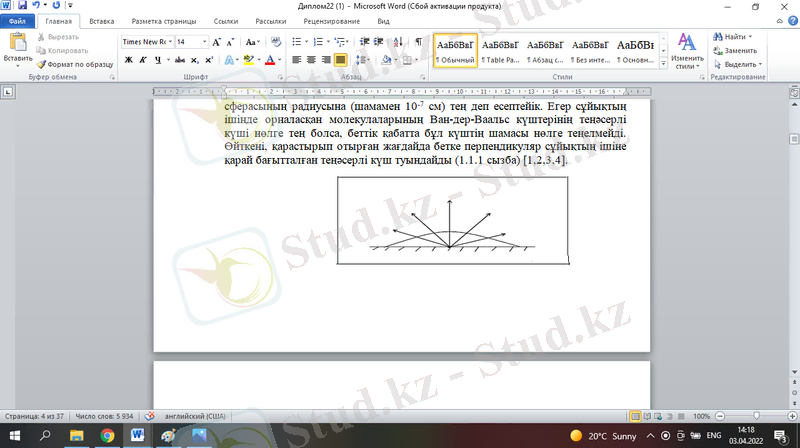
$C:\Users\user\Pictures\Screenshots\24.png$

1. 1. 1 сызба. Беттік керілу күшінің пайда болуы.

Беттік қабаттағы әрбір молекуланы оны сұйықтың ішіндегі қабаттарға тартуға тырысатын күш пайда болады. Беттік қабаттағы молекулаға әсер ететін күштерді квадранттар бойынша топтасақ, бұл күштер (1. 2. 1 сызбасында) көрсетілгендей күштердің тік және горизонталь жазықтықтардағы кұраушыларынан тұрады. Тік жазықтықтағы күш молекуланы сұйықтың ішіне қарай тартса, ал горизонталь жазықтықтағы күштің құраушысы сұйықтың бетін кемітуге ұмтылады. Келтірілген күш беттік керілу күші деп аталады. Беттік керілу күшіне мөлшерлік сипаттама беру мақсатында сұйықтың бетінен ойша ұзындығы бір сантиметр кесіндіні (1. 2. 2 сызба) бөліп алайық. Сұйық өзінің бетін осы кесіндіге қарай кемітуге ұмтылатындықтан, яғни, кесіндіде орналасқан молекулаларға оған перпендикуляр бағытталған беттік қабаттың жазықтығында жататын күш әсер етеді. Бір жаққа қарай бағытталған осы күштердің бірлік кесіндіге әсер ететін тең әсерлі күшін σ арқылы белгіленіп, беттік керілу коэффициенті деп атаймыз. [5-8] :

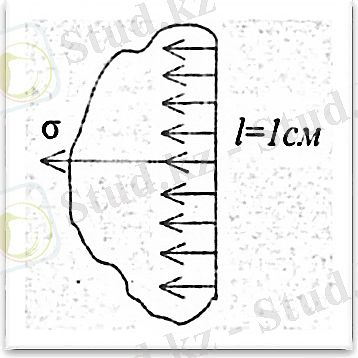
сызба. Беттік керілу коэффициентінің анықтамасы

Беттік керілу коэффициентіне басқа анықтама беру үшін мынандай тәжірибе (1. 1. 3 сызба) жасаймыз.

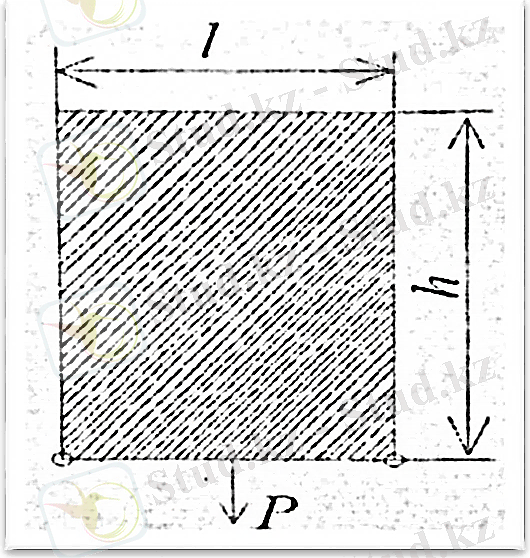
сызба. Сұйық бетінің пайда болуы [9. 10]

Сымнан жасалған кәсектің бағыттаушы қабырғаларының бойымен еркін қозғалатын жеңіл көлденең сым кигізіп, оны сабын ерітіндісі бар ыдысқа салып сабынның жұқа қабығы бар кәсекті созамыз. Өзінің бетінің ауданын кемітуге ұмтылуының салдарынан жұқа қабық көлденең сымды жоғары көтереді. Жоғары бағытталған беттік керілу күші $\sigma_{21}$ тең. Мұндағы, кәсектің ені. Жұқа қабықтың екі беті бар болғандықтан кәсектің екі еселенген ені алынады. Беттің керілу күшін көлденең сымға салмағы Р жүк алу арқылы теңестірсек, яғни Р=2σl. Жүк керілген жұқа қабыққа түсіріледі деп алып, тепе- теңдік күйге жеткенде, оны Δh-қасозатын элементар керілу жұмысы мынаған тең: [7-10]

dA=Pdh=2lσdh= σdS

Мұндағы, S=2ldh жұқа қабықтың бетінің өсімшесі. Бұдан:

$\sigma = \frac{dA}{dS}$

(1. 1. 1)

Белгілі бір себептермен сұйықтың беті ұлғайсын делік. Яғни, молекулалардың қандайда бір мөлшері сұйықтың ішінен беткі қабатына көтеріледі. Ол үшін сыртқы жұмыс істелінуі қажет. Демек, сұйықтың бетінің ұлғаюы теріс жұмыс жасалуы арқылы жүзеге асырылады. Керісінше, сұйықтың беті кемігенде оң жұмыс істелінеді. Тұрақты температурада қайтымды жолмен сұйықтың бетін шексіз кіші dS бетіне өзгертетін жұмыс мынаған тең [10-12]

dS=-σdS (1. 1. 2)

Теріс таңба беттің ұлғаюы (dS> 0) теріс жұмыспен іске асырылатындығын көрсетеді. $\sigma$ беттің керілу коэффициенті, ол сұйықтың бетін сипаттайтын негізгі (σ > 0) шама болып табылады. Сондықтан, беттің керілу коэффициенті тұрақты температурада сұйықтың бетінің ауданын, бірлік ауданға ұлғайту үшін кеткен жұмысқа тең. Cондықтан, сұйықтың беттік қабатында орналасқан молекулалардың оның төмендегілермен салыстырғанда артық потенциялдық энергиясы бар. Демек, сұйықтың бетінің оның қалған бөлігінің массасымен салыстырғанда потенциялдық энергиясы артық. Кез-келген жүйе орнықты болуы үшін оның энергиясы минимал мәнді иеленуі қажет. Біз қарастырып отырған жағдайда сұйық тепе-теңдік күйде болатын ең кіші бетті қабылдауы тиісті. Бұл сұйық бетінің ұлғаюына кедергі жасайтын, яғни оның бетін кемітетін күш әсер ететінін көрсетеді. Сұйықтың бетін кемітетін күштердің бағыты бетке жүргізілген жанамамен бағытталады. Бұл күштерді беттік керілу күші деп атайды. Жоғарыда құрастырылған кәсектегі сабын ерітіндісінің жұқа қабығының керілуіне термодинамиканың екінші заңын (1. 1. 4 сызба) қолданайық

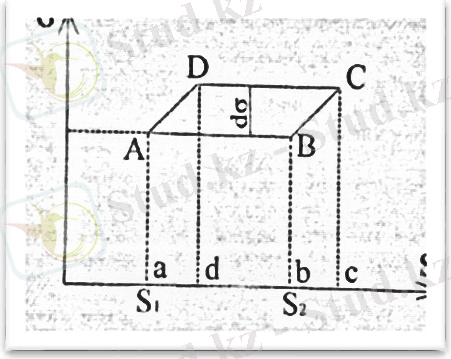
сызба. Беттік керілу коэффициентінің температураға тәуелділігін

қорытып шығаруға арналған сызба [5]

Құбылысты зерттеуді жеңілдету мақсатында жұқа қабық таза судан тұрады деп аламыз. (Мұндай жұқа қабық орнықсыз) . Жұқа қабықтың бетін керіп, ұлғайтып, содан соң қайта кішірейтіп Карно циклін жазайық. σ - S координатасындағы жұқа қабықтың t температурадағы бастапқы күйі А нүктесімен кескінделсін. Жұқа қабыққа δQ жылу мөлшерін беру арқылы оны изотермалық созып, ауданын ∆S=S ₂ -S ₁ арттырамыз. Жаңа күй В нүктесіне сәйкес келеді. Ал істелінетін dA=σdS жұмысы AB S ₂ S ₁ ауданымен

кескінделеді. Изотермалық созу кезінде беттік керілу коэффициенті өзгермейді. Жұқа қабық В күйге жеткеннен кейін оны шексіз қашықтыққа созғанда температурасы dT шамасына төмендеп, ал беттік керілу коэффициенті dσ артады. Жаңа күй С нүктесімен кескінделеді. Енді жұқа қабықтың D күйге дейін изотермалық кішірейуіне мүмкіндік берейік. Содан кейін жұқа қабық бастапқы А күйге келгенше кішірейуі адиабаталық түрде өтеді. Адиабаталық ұлғаю жұмысы bBCc ауданына, ал изотермалық кішірею жұмысы CcDd ауданына, адиабаталық кішірею жұмысы dDAa ауданына тең. Циклдің жұмысы жұқа қабықтың кішірейгенде және созылғанда істелетін АВСД ауданына сәйкес келетін (S ₂ - S ₁ ) dσ айырымына тең. Қыздырғыштан алынған жылу мөлшерінің шамасы δQ болса, циклдың пайдалы әсер коэффициенті мынаған тең [5-16] :

$\eta = \frac{\left( S_{2} - S_{1} \right) d\sigma}{\delta Q}$ (1. 1. 3)

Жұқа қабықты сыртқы күштің әсерімен созғанда істелетін теріс жұмыс қыздырғыштан оң δQ жылуын алу, ал кішірейгендегі оң жұмыс циклдің теріс таңбасымен алынған (S ₂ - S ₁ ) dσ жылудың бөлінуімен жүзеге асырылады. Идеал Карно циклінің формуласын пайдаланып, мына қатынасты аламыз [16-18] :

$\eta = \frac{\mathrm{\Delta}Sd\sigma}{\delta Q} = \frac{dt}{t}$ (1. 1. 4)

Мұндағы, dt=t ₁ -t ₂ немесе беттің бірлік ауданының туындауына жұмсалған жылу мөлшерін $\ \ \ \frac{\delta Q}{\mathrm{\Delta}S} = r$ деп алсақ, төмендегі қатынас шығады: [17]

$\frac{d\sigma}{dT} = - \frac{r}{T}$ (1. 1. 5)

демек, температура жоғарылағанда беттік керілу коэффициентінің шамасы кеміп, кризистік нүктеде нөлге теңеледі. Сұйықтың қисық бетінің қысымын анықтау үшін тамшының бетінен ∆S элементтері (1. 1. 5 сызба) бөліп аламыз. [17-18]

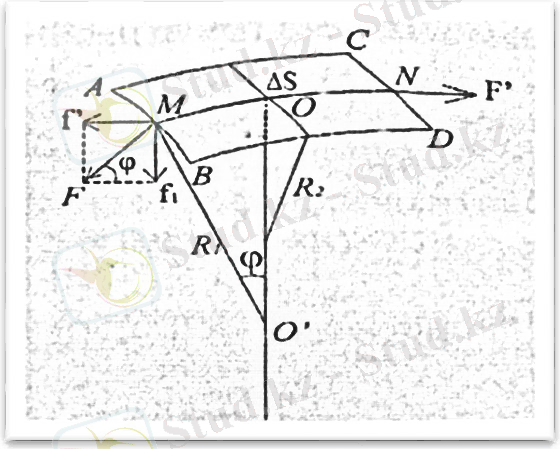
1. 1. 5 сызба. Сұйықтың қисық бетінің қысымы

Элементтің бетін шектейтін АВ және CD сызықтарына түсірілген беттік керілу күшін есептейміз. Беттік керілу күші сызықтарға перпендикуляр бағытталып, беттің ∆S элементіне жүргізілген жанаманың бойында жатады. Осы күштердің қисықтың центріне бағытталған құраушысын анықтайық. Бетке перпендикуляр қисықтық радиусына параллель бағытталған бұл күш іште жатқан аймақтың беттік қабатындағы қысымды арттырады. Егер бет жазық болса, күштің нормалдық құраушысы жоқ. Барлық күштер беттік қабаттың жазықтығында жататындықтан, қосымша қысым туындамайды. АВ ұзындығына түсіретін F күші мынаған тең:[17-18]

F = AB ∙ σ (1. 1. 6)

АВ және МО сызықтарында ОО' сызығымен қиылысқанша перпендикуляр жүргізіп, осы бағыттағы беттің қисықтық R ₁ радиусын аламыз. Содан соң екінші қисықтық радиусы R ₂ алу үшін BD сызығына ОО' сызығымен қиылысқанша перпендикуляр жүргіземіз. Қисықтық радиустары әртүрлі болғандағы жалпы жағдайды қарастырайық. F күшін ОО' сызығына параллель бағыттағы Р қысымын анықтайтын f ₁ , күшке және осы күшке перпендикуляр біз қарастырып отырған жағдайда ескерілмейтін f' күшке жіктейміз. F және f’ арасындағы бұрышты ϕ арқылы (ϕ =< МО'О) белгілесек, төмендегі қатынастар шығады:

$f_{1} = Fsin\varphi = \sigma AB\frac{MO}{R_{1}} = \frac{\mathrm{\Delta}S\sigma}{2R_{1}}$ (1. 1. 7)

Өйткені, $AB \bullet MO = \frac{\mathrm{\Delta}S}{2}$

күшін осындай екі қараушыға жіктеп, мына формуланы аламыз:

$f_{2} = CD\sigma\frac{NO}{R_{1}} = \frac{\mathrm{\Delta}S}{2R_{1}}$

(1. 1. 8)

BD және AC бөліктері үшін де (R ₁ -дің орнына R ₂ алынады) осы өрнек алынады. Барлық төрт өрнекті қоссақ, мына формула шығады:[15-17]

$\sum_{i}^{}{f = \mathrm{\Delta}S\sigma(\frac{1}{R_{1}} + \frac{1}{R_{2}}})$ (1. 1. 9)

Қисық беттің қысымы төменгі формуламен есептеледі [17] :

$P = \frac{\sum_{i}^{}{ifi}}{\mathrm{\Delta}S} = \sigma(\frac{1}{R_{1}} + \frac{1}{R_{2}})$

(1. 1. 10)

(1. 1. 10) өрнегі Лаплас формуласы деп аталады.

Дербес жағдайда мысалы, тамшының пішіні сфера тәріздес болса, формула мынандай болып түрленеді:[15-17]

$P = \frac{2\sigma}{R}$

(1. 1. 11)

Егер сұйықтың бітінің пішіні цилиндр тәріздес болса, яғни радиустардың біреуі шексіздікке ұмтылғанда Лаплас формуласы төмендегідей түрленеді [6-10] :

$P = \frac{\sigma}{R}$ (1. 1. 12)

Келтірілген формулалар судан тұратын тамшы немесе сұйықтың ішінде орналасқан көпіршік үшін орындалады. Көпіршіктің (мысалы, сабын көпіршігі) оның ішіндегі газға түсіретін қысымы жоғарыдағылардан екі есе артық. Себебі көпіршіктің сыртқы және ішкі қабаттары бірдей қысымдар туғызады. Сондықтан толық қысым мына формуламен өрнектеледі [7-14] :

$P = \frac{4\sigma}{R}$

Сұйықтың беті цилиндірдің пішінін қабылдағанда өрнек төмендегідей [8, 9] түрленеді:

$P = \frac{2\sigma}{R}$

Қосымша қысым радиусқа кері пропорционал болғандықтан, көпіршік кішірейген сайын қысым артады.

Бір-бірімен араласпайтын сұйық тамшысының басқа сұйықтың бетіндегі күйіне талдау (1. 1. 6 сызба) жасайық [16, 17, 18] :

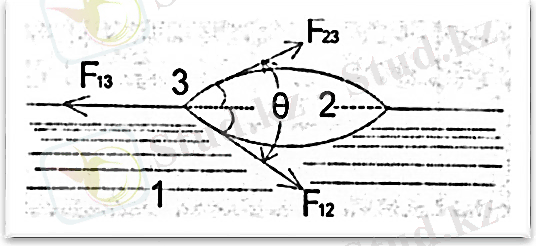
1. 1. 6 сызба. Басқа сұйықтың бетіндегі жұқпайтын сұйық тамшысының күйі[17, 18]

Ауыр сұйықтың (1) бетіндегі түскен жеңіл сұйықтың (2) тамшысы

линзаның пішінін қабылдайды. Тамшы әр түрлі үш ортамен жанасады. Оның екеуі 1 және 2 сұйықтық, біреуі 3 газ (ауа) . Әрбір екі ортаны бөлетін беттерде сол беттерді кішірейтуге ұмтылатын беттік керілу күштері пайда болады. Үш ортаның жанасу шекарасы жасымықты (чечевица) шектейтін шеңбер болып табылады. Осы шебердің ұзындығы dl элементіне үш беттік керілу күші әреке етеді:күші.

F ₁₂ = σ ₁₂ dl - 1-ші және 2-ші сұйықтардың шекарасындағы беттік керілу

F ₂₃ = σ ₂₃ dl - 2-ші сұйық 3-ші газдың шекарасындағы керілу күші. F ₁₃ =

σ ₁₃ dl - 1-ші сұйық пен 3-ші газдың шекарасындағы беттік керілу күші. Газ тәріздес ортаның сұйықтың беттік энергиясына әсері ескерілмейтіндіктен, σ ₁₃ = σ ₁ , σ ₂₃ = σ ₂ деп аламыз. 2-ші сұйықтың тепе-теңдік күйде болуы үшін координаталар өсіндегі барлық күштердің құраушыларының қосындысы нөлге теңелуі қажет. Сондықтан, төменде келтірілген теңдіктер орындалады [17-18] :

$F_{13} = F_{23}$ cos $\theta_{1} + F_{12}\cos\theta_{2},$ $F_{23}\sin\theta_{1} - F_{12}\sin\theta_{2} = 0$ (1. 1. 13)

Немесе

$\sigma_{13}^{2} + \sigma_{23}^{2} + \sigma_{12}^{2} = \sigma^{2} + \sigma^{2} + 2\sigma_{23}\sigma_{12}\cos\theta_{1}\cos\theta_{2} - sin\theta_{1}\sin\theta_{2}$ (1. 1. 14)

теңдеулерін квадраттап қоссақ, мына өрнек шығады:

$\sigma_{13}^{2} + \sigma_{23}^{2} + \sigma_{12}^{2} + 2\sigma_{23} + \sigma_{12}\cos\theta_{1}\cos\theta_{2} - sin\theta_{1}\sin\theta_{2}$

немесе

$\sigma_{13}^{2} = \sigma_{23}^{2} + \sigma_{12}^{2} + 2\sigma_{23}\sigma_{12}cos(\theta_{1} + \theta_{2})$

𝜃1 + 𝜃2 = 𝜃 ескерссек, мына формуланы аламыз:[17, 18]

$\sigma_{13}^{2} + \sigma_{23}^{2} + \sigma_{12}^{2} + 2\sigma_{23}\ \bullet \sigma_{12} \bullet cos\theta$

(1. 1. 13) және (1. 1. 14) теңдеулерін пайдаланып, 𝜃 ₁ , 𝜃 ₂ және 𝜃 ₁ + 𝜃 ₂ = 𝜃 бұрыштарын табуға болады. 𝜃 ₁ және 𝜃 ₂ бұрыштар шеттік бұрыштар деп аталады. Тепе- теңдік күйдегі жанасатын сұйықтардың шекараларындағы шеттік бұрыштар үш коэффициентінің δ ₁₂ , δ ₁₃ , δ ₂₃ қатынасары немесе әрбір сұйықтың ішіндегі және сұйықтың арасындағы молекулярлық күштердің қатынасымен анықталады. Дербес жағдайда δ ₁₂ , δ ₁₃ , δ ₂₃ араларындағы қатынас мынадай болуы мүмкін cos 𝜃 = 0 яғни 𝜃 = 0. Бұл жағдайда 2-ші сұйық 1-ші сұйықтың бетімен жұқа қабатпен ағады. Яғни, бірінші сұйық екінші сұйыққа толық

(немесе керісінше) жұғады. Физикалық тұрғыдан қарағанда аталған құбылыста мына теңсіздік орындалу керек

𝐹 ₁₃ = 𝐹 ₁₂ + 𝐹 ₂₃ (1. 1. 15)

1. 1. 6 сызбасынан қарастырып отырған жағдайда қорытқы күш тамшыны керуге бағытталған.

F ₂₃ + F ₁₂ > F ₁₃ болғанда тамшы жасымықтың шарты орындалғанша жиырылатындықтан, төменгі теңдік орындалады: :[15, 18]

F ₁₃ = F ₂₃ + F ₁₂ (1. 1. 16)

Қатты денелердің молекулаларының өзара тартылыс күштерінің әсерінен кристалдық тор туындайды. Осы күштердің бар болуының салдарына қатты денелерде беттік керіле күші пайда болады. Тамшы қатты дененің үстіне (№1. 1. 7 сызба) орналасқанда екі жағдай болуы мүмкін.

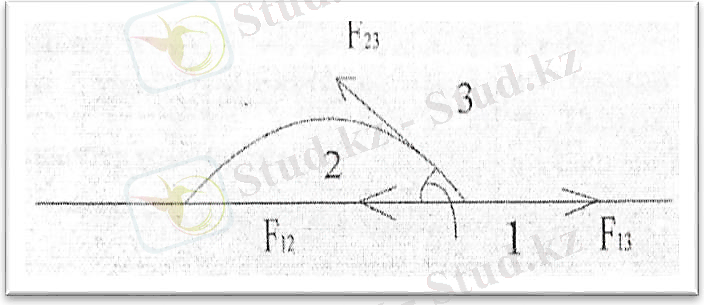
сызба. Жұғатын сұйық тамшысының қатты денелердің бетіне орналасуы [10-18]

Бірінші жағдайда қатты дене мен газ шекарасындағы беттік керілу F ₁₃ күші қатты денемен сұйықтың шекарасындағы беттік керілу F ₁₂ күшпен горизонталь жазықтықтағы F ₂₃ cosӨ қарушысының қосындысынан үлкен. Қарастырып отырған жағдайда F тамшы қатты бетте (оның барлық бетін жапқаншы) F ₁₃ = F ₁₂ + F ₂₃ cos𝜃 теңдігі орындалғанда жайылады. F ₁₃ ≥ F ₁₂ + F ₂₃ болғанда тепе-теңдік орнамай сұйық қатты дененің бетімен оның бетін толық жапқанша немесе мономолекулалық қабат пайда болғанша жайылады. Яғни, сұйық қатты денеге абсолютті жұғады. Бұл жағдайда шеттік 𝜃 бұрышы нөлге тең. Егер 𝜃 бұрышының қандайда бір мәндерінде F ₁₃ = F ₁₂ + F ₂₃ cos𝜃 теңдігі орындалса, жұғу абсолютті немесе толық (𝜃< 90°С) емес деп аталады. 𝜃< 90°C болғанда (1. 2. 8 сызба) F ₂₃ cos𝜃 беттік керілу күші F ₁₂ күшімен бірге тамшыны жиырылып сфералық пішін қабылдатуға (ауырлық күші кедергі жасайтын) ұмтылдырады. [10-18]

1. 1. 8сызба. Қатты дененің бетіне жұқпайтын сұйықтың тамшысы

Соңғы жағдайда 𝜃> 90°Сболғандықтан, F ₂₃ cos𝜃 мүшесі теріс.

Сондықтан тепе-теңдік шарты мына теңсіздікті қанағаттандырады:

F ₁₃ <F ₁₂ - F ₂₃ cos𝜃

Бұл (cos𝜃= -1) шарт шынының бетіндегі кішкентай сынап тамшысы үшін (сынап шыныға мүлдем жұқпайды) дұрыс. Осыған қарсы құбылысты таза шынының бетіндегі судың немесе спирттің тамшысынан байқауға болады. Су мен спирт шыныға толық жұғатындықтан, оның бетімен шексіз жайылады. Бір сұйықтың екінші сұйықтың бетіне жайуын судың бетіне мұнайдың бірнеше тамшысын жібергенде байқаймыз. Мұнайдың бірнеше тамшысы шексіз жайылса, екінші және одан кейінгі тамшылар жайылмай бетте линзаның пішінін қабылдайды. Өйткені бірінші тамшы жарым- жартылай сумен адсорбцияланып, соңғыларының беттік керілу күштерініңкемуіні салдарынан тепе-теңдік күй орнығып, тамшы жайылмайды. Жұқпайтын сұйық өте кіші саңылау арқылы ақпай, онда ілініп тұрады. (1. 1. 9 сызба) [11612613] .

1. 1. 9 сызба. Кіші саңылаудан жұқпайтын сұйықтың ақпауы

Егер елеуіштің төменгі жағына суланған затты елеуіштің жоғарығы және төменгі жағындағы жанасатындай етіп орналастырсақ, су жылдам ағады. Егер саңылау үлкен болса, су сорғалап ағады. Кішкентай саңылаудан немесе сұйықтың гидродинамикалық ағыны аз болғанда сұйық тамшылап ағады.

Тамшының массасы артқан сайын онда пайда болған мойын жіңішкеріп тамшы үзіледі. (1. 1. 10 сызба) [14]

1. 1. 10сызба. Тамшының пайда болуы [17-18]

Тамшының массасы мен беттік керілу коэффицентінің және тамшының мойнының радиусының аралығындағы байланыс формуласын жазайық. Тамшы үзілетін кезде ауырлық күші беттік керілу күшіне теңеледі [15, 16, 17] :

Mg=2πrϭ

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.