Түйіндесу

Пән: Полиграфия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

II. Түйіндесу - a сызығынан b сызығына үшінші с сызығының көмегімен біртіндеп өтуді айтады (22, а-сурет) . Мұнда a және b сызықтары беріледі де, олардың бойынан А және B нүктелерін тауып, оларды с сызығының кесіндісімен қосу керек. Берілген а және b сызықтарын түйіндесетін сызықтар деп, ал олардың А және В нүктелерін түйіндесу нүктелері деп және с сызығын түйіндестіретін сызық деп атаймыз. Енді «біртіндеп өтуді» түсіндірейік. Бұл терминді былайша түсінетін боламыз. Түйіндесетін а сызығы мен түйіндестіруші с сызығының ортақ нүктесі А арқылы өтетін жанамалары бірігулері тиіс. Сол сияқты b және c сызықтарының ортақ нүктесі B арқылы жүргізілген жанамалары да бірігулері тиіс.

Біздер түйіндестіретін сызық шеңбердің доғасы, ал түйіндесетін сызықтар түзулер немесе шеңбердің доғалары болатын жағдайларын ғана қарастырамыз.

Берілген a және b сызықтарын түйіндестіру үшін түйіндесу нүктелерін, түйіндестіретін шеңбердің радиусын және центрін анықтап алу керек. Осы аталған түйіндестіру элементтерінің біреуі берілсе, басқаларын анықтап алуға болады. Көбіне түйіндестіретін шеңбердің радиусы беріледі, оның центрін және түйіндесу нүктелерін анықтауға тура келеді.

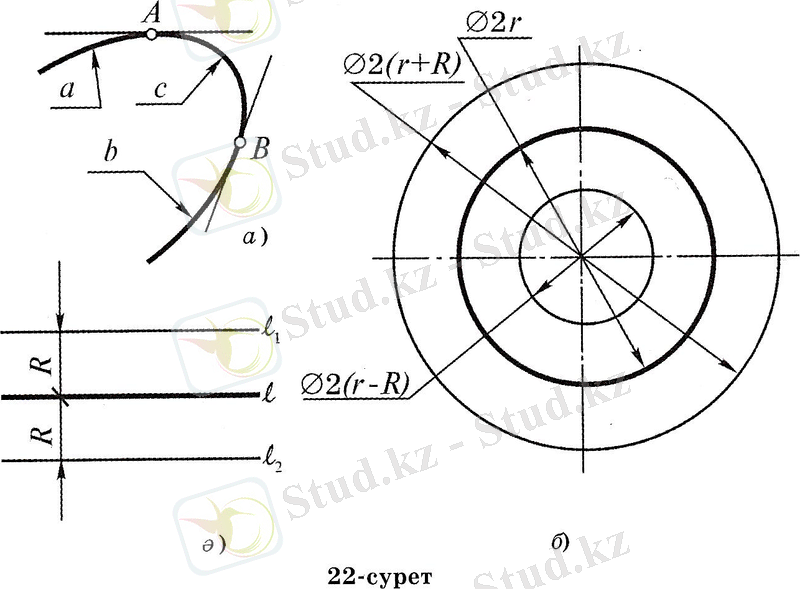
Түйіндесетін сызық шеңбер болса, түйіндестіретін шеңбердің центрі түйіндесу нүктесін берілген шеңбердің центрімен қосатын түзудің бойында жатады. Түйіндесетін сызық түзу сызық болса, түйіндестіретін шеңбердің центрі түйіндесу нүктесі арқылы берілген түзуге перпендикуляр етіп жүргізілген түзу бойында болады.

Берілген түзу екінші бір сызықпен радиусы R шеңбер арқылы түйіндесетін болса, оның центрі берілген түзуден қашықтығы R-ге тең, оған параллель екі түзудің біреуінің бойында жатады(22, ә-сурет) .

Берілген радиусы r-ге тең шеңбер екінші бір сызықпен радиусы R-ге тең шеңбер арқылы түйіндесетін болса, онда оның центрі берілген шеңбердің центрінде, радиустары r + R және r - R болатын екі шеңбердің біреуінің бойында жатады(22, б-сурет) .

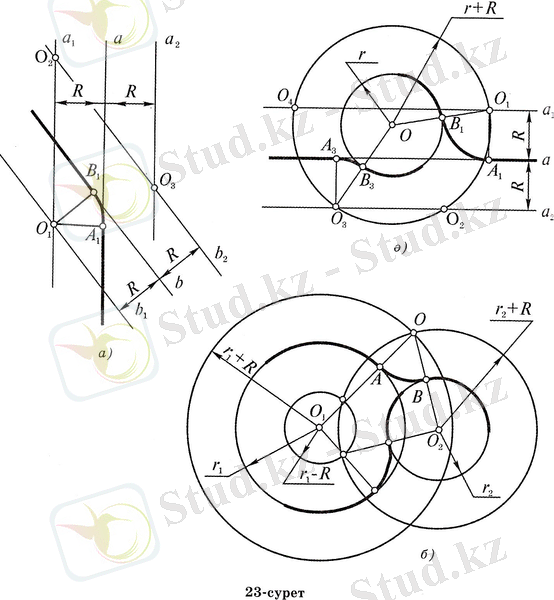
Берілген екі түзудің радиусы R-ге тең шеңбермен түйіндесуі(23, а сурет) . Түйіндестіретін шеңбердің центрін іздейміз. Ол а түзуіне параллель, одан R қашықтықта орналасқан а1және а2түзулерінің біреуінің бойында жатуы тиіс. Дәл осы сияқты іздеп отырған центріміз b түзуінен R қашықтықтағы b1және b2түзулерінің біреуінің бойында жатуы тиіс. Ал a1, a2, b1және b2түзулері төрт нүктеде қиылысады. Сондықтан есептің төрт шешуі болуы мүмкін. Мысалы, түйіндестіретін шеңбердің центрі ретінде О1нүктесі алынсын. Түйіндестіру центрі табылғаннан кейін түйіндесу нүктелерін анықтау керек. Ол үшін О1нүктесінен a және b түзулеріне перпендикуляр түзулер жүргіземіз. Осы перпендикуляр түзулер a және b түзулерін А1және В1нүктелерінде қияды. Енді шеңберсызармен, оның инесін О1нүктесіне қадап, түйіндесу нүктелері А1мен В1-ді шеңбердің доғасымен қосса болғаны.
Берілген түзуді және радиусы r шеңберді радиусы R шеңбер доғасымен түйіндестіру(23, ә-сурет) . Түйіндестіретін шеңбердің центрін іздейміз. Ол үшін а түзуіне параллель, одан R қашықтықтағы а1және а2түзулерін жүргіземіз және центрі О нүктесі, ал радиустары r + R және r - R болатын екі шеңбер жүргіземіз. Өзара параллель екі түзу бір центрден жүргізілген екі шеңберді жалпы алғанда 8 нүктеде қиюы мүмкін. Бірақ бұл нүктелердің кейбіреулері жорамал болады. Мысалы, егер r < R болса, онда радиусы r - R шеңбер жорамал болады. Сызу пәнінде нақты (жорамал емес) нүктелер мен сызықтар қарастырылады. Біз түйіндестіретін шеңбердің центрі ретінде а1түзуімен радиусы r + R шеңбердің қиылысу нүктелерінің бірі О1нүктесін алайық. Осы О1нүктесінен а түзуіне түсірілген перпендикулярдың табаны А1және О1О түзуінің берілген шеңбермен қиылысу нүктесі В1түйіндесу нүктелері болады. Табылған А1және В1нүктелерін центрі О1нүктесінде жататын шеңбер доғасымен қосамыз.
Берілген екі шеңберді радиусы R доғасымен түйіндестіру. Берілген шеңберлердің біріншісінің центрі О1нүктесі, радиусы r1 болсын, ал екіншісінің центрі О2нүктесі радиусы r2болсын(23, б-сурет) . Төрт шеңбер жүргіземіз. Олардың екеуінің центрі O1нүктесінде, ал радиустары r1+ R және r1- R болады. Қалған екеуінің центрі О2нүктесінде, ал радиустары r2+ R және r2- R болады. Бұл төрт шеңбер 8 нүктеде қиылысуы мүмкін. Алайда, олардың біразы - жорамал нүктелер. Іздеп отырған түйіндестірудің центрі ретінде О нүктесін алайық. ОО1мен ОО2кесінділерін жүргізсек, олар берілген шеңберлерді А және В нүктелерінде қияды. Түйіндестіру центрі О мен түйіндесу нүктелері А және В табылғаннан кейін, түйіндестіретін шеңбердің доғасын жүргізуге болады.
Шеңберлер доғаларын түйіндестіру нәтижесінде алынған тұйық сызықты -сопақша(овал) деп атайды.

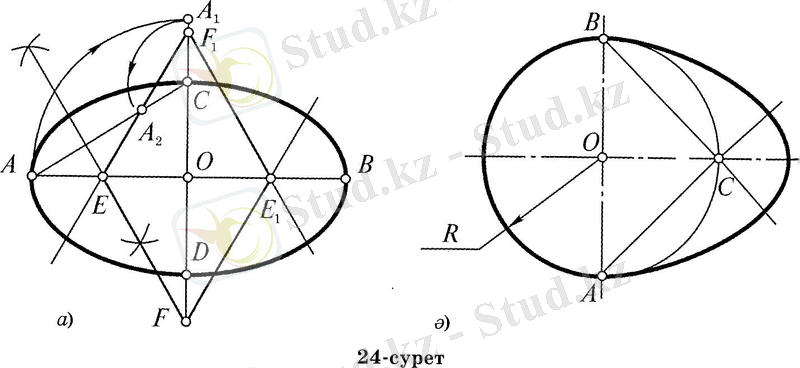
Сопақшаларды біросьті және екіосьті деп ажыратады. Екіосьті сопақша осьтерінің ұзындықтарымен анықталады. Үлкен осі a, кіші осі b болатын сопақша жүргізелік(24, а-сурет) . Ұзындықтары a және b-ге тең өзара перпендикуляр және бір-бірін О нүктесінде қақ бөлетін АВ мен CD кесінділерін жүргіземіз. Центрі О нүктесінде жататын А нүктесі арқылы өтетін шеңбер жүргізсек, ол CD кесіндісінің созындысымен А ₁ нүктесінде қиылысады. Центрі С нүктесінде жататын, А ₁ нүктесі арқылы өтетін шеңбер жүргізсек, ол АС кесіндісін А ₂ нүктесінде қияды. АА ₂ кесіндісінің ортасына перпендикуляр жүргізсек, ол үлкен осьті Е нүктесінде, кіші осьтің созындысын F нүктесінде қияды. Табылған Е және F нүктелеріне симметриялы Е ₁ және F ₁ нүктелерін саламыз. Төрт сәуле FE, FE ₁ , F ₁ E және F ₁ E ₁ жүргіземіз. Центрі F ₁ нүктесі болатын және D нүктесі арқылы өтетін шеңбер доғасын F ₁ E және F ₁ E ₁ сәулелері аралығында жүргіземіз. Центрі F нүктесінде болатын және C нүктесі арқылы өтетін шеңбердің доғасын FE және FE ₁ сәулелері аралығында жүргіземіз. Бұл екі доғаны центрі Е нүктесінде жататын және А нүктесі арқылы өтетін, центрі Е ₁ нүктесінде жататын және В нүктесі арқылы өтетін екі доғамен тұйықтаймыз.

24, ә-суретте кескінделгендей біросьті сопақша сызып көрсетейік. Радиусы берілген кесінді R-ге тең шеңбер жүргіземіз. Сопақшаның осін жүргізейік, ол ОС түзуі болсын. Шеңбердің оське перпендикуляр АВ диаметрін саламыз. АС және ВС сәулелерін жүргіземіз. Енді центрлері А және В нүктелерінде жататын, радиустары 2R-ге тең екі шеңбер жүргізіп, олардың АС және ВС сәулелерімен қиылысу нүктелерін центрі С нүктесінде болатын шеңбердің доғасымен қосамыз.

Жоспар