Синусоидалық ток: сипаттамалар және тізбектегі индуктивтік пен сыйымдылық элементтер


Жоспар:
- Синисоидалық ток және оны сипаттайтын негізгі шаралар.
- Синусоидалық ток тізбегіндегі индуктивтілік элементі.
- Синусоидалық ток тізбегіндегі сыиымдылық элементі.
Қорытынды
Қолданылған әдебиеттер
Синусоидалық ток және оны сипаттайтын негізгі шаралар.
Өзінің бағыты және шамасы периодты түрде өзгеріп отыратын токты (кернеуді) айнымалы деп атайды. Біз білетіндей тұрғын үй жүйелеріін жарықтандыруда, сол сияқты заводтар мен фабрикаларда қолданылатын айнымалы ток, еріксіз электро магниттік тербелістердің түріне жатады. Демек, ток және кернеу уақыттан тәуелді гармониялық заңмен өзгереді.
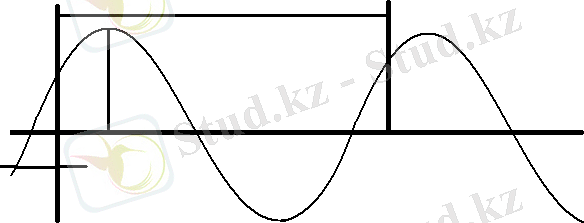
Синусдалы ток уақытқа байланысты синусоидалық заңмен өзгереді
I=i m sin(2пt/T+Ψ) =I m sin(Ψ) 6
Функцияның максимал шамассын амплитуда деп атайды. Токтың амплитудасын I m әрпмен белгілейді. Толық бір тербеліс жасауға кететін уақытты период деп атайды. Оны Т әрпімен белгілейд.
Т
I m
T/2 T t
П 2п I
Ψ
Бір секундтағы тербелістер оны жиілік деп атайды. Оны f әрпімен белгілейді. Сонда жиіліктің өлшем бірлігі - Гц - герц немесе с -1 .
F=1/T
Бұрыштық жиілікті мен белгілейді. Оның өлшем бірлігі - рад/с немесе с -1 .
=2п f=2п/T
өрнегінің синустың аргументінін, яғни (t+Ψ) -ді фаза деп атайды. Фаза t-уақыт кезіндегі тербелістің күйін (сан мәнін) сипаттайды.
Синусоида заңмен өзгеретін кез-келген функция үш шамамен: амплитуда, бұрыштық жиілік және бастапқы фазамен анықталады.
ТМД және батыс Еуропа елдерде, енергетикалық стандарт ретінде синусоидалық токтың жиілігіне 50Гц қабылданған. АҚШ-та сандарттық жиілік 60 Гц тең. Практикада қолдау тапқан синусоидалық токтардың жиілік диапазондары өте көп. Ол мысалы геологиялық барлауда герцтың үлесінен басталса, радиотехникада миллиардтаған герцке дейін барады.
Синусоидалық токтар мен ЭҚК-і көздерін және ток көздерін электрлік схемаларда тұрақты ЭҚК-і көзі және ток көздері белгілеуге ұқсас белгілейді. Былайша айтқанда, оларды е және J (немесе (t) және J (t) ) деп белгілейді.
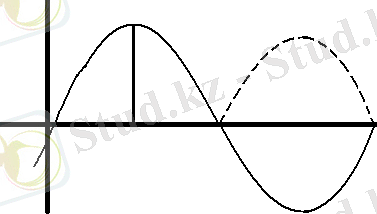
Жоғары математикада f (t) периодттық функцияның Т -периодындағы орташа мәнін мынандай өрнекпен анықталатыны бізге белгілі:
F=1/ T 0 f(t) dt.
Мұнда біз, функцияның бір период ішіндегі орташа шамасы, ауданы f(t) функциясымен шектелген, абцисса осі бір периодқа тең, тік бұрыштың биіктігі Т - табанына көьейткенге тең ауданымен анықталатынын көреміз.
F(t)
2/п А
t
0 T/2
Синусоидалық функция жағдайында период ішіндегі оның мәні 0-ге тең. Себебі, синусоидының жарты толқынының оң таңбалы ауданы синусоиданың келесі теріс таңбалы жарты толқынның ауданымен теңгеріледі. Сондықтан обсолют шамасы бойынша алынған функцияның орташа мәні, немесе сондай орташа жарты периодтық мәні алынады. Ол синуоидының оң таңбалы жарты толқынына сәйкес келеді.
Демек, осыған сәйкес амплитудасы А =I m синусоидалық токтың орташа мәні былай анықталады:
I=I m /(T/2) T 0 sin d t = 2I m / T(-cos t) T 0 =2/п I m ≈ 0. 6381 m
Демек, синусоидалық токтың орташа мәні аплитудалық токтың 0, 638 бөлігін құрайды. Осыған ұқсас
E орт =2E m /п; U орт =2 U m /п ≈ 0. 638 U m
Токтың жылулық әсері және сол сияқты бірдей ток өтетін екі өткізгіштердің механикалық өзара әсерлесулерінің күші, токтың квадратына пропорционал болады. Сондықтан токтың шамасын период ішіндегі әсерлік (орташа квадраттың) мәні бойынша бағалайды.
Бұдан әрі біз математикаға жүгінсек, f(t) периодтық функциясының әсерлік мәнін былай анықтаған болар едік:
F=√1/T T 0 [f(t) ] 2 dt
Өрнегін синусоида заңымен өзгенретін токқа қолдансақ, онда токтың әсерлік мәнін былай жазуға болады:
I=√1/T T 0 [f(t) ] 2 dt=√1/ T 0 I m sin 2 wtdt=I m/ √2
Бұл жерде, біз синусоидалық токтың әсерлік мәні, оның аплитудалық мәнінің 0, 707 бөлігін құрайтынын көреміз. Осыған ұқсас
E=E m /√2 және U=U m /√2
Белгілі бір кедергі арқылы бірдей уақыт аралығында жүріп өтетін синусоидалық токпен тұрақты токтың жылулық әсерлерін салыстыруға болады.
Бір периодта синусоидалық токтан бөлінетін жылудың мөлшері
T 0 Ri 2 dt=RI 2 m T/2
Сондай уақыт аралығында тұрақты токтың бөлінетін жылуы RI 2 тұр Т болады. Бұларды теңестірсек:
RI 2 m T=RI 2 тұр =I=I m/ √2
Сонымен, синусоидалық токтың әсерлік мәні (I) сан жағынан, синусоидалық токтың периодына тең уақыт ішінде, сондай синусоидалық токтың бөлінетін жылуындай жылу шығартын, тұрақты токтың мәніне тең болады.
Практикада қолданылатын көптеген өлшеуге арнылған электрлік құралдыр, өлшенетін шаманың әсерлік мәнін көрсетеді.
Периодтты түрде өзгеретін функциясының аплитудасының оның әсерлік мәніне қатынасын аплитудалық коэфицент деп атайды. Оны
k a =I m /I=√2
сол сияқты периодты түрде өзгеретін функцияны әсерлік мәнінің оның жарты период ішіндегі орташа мәніне қатынасын, формалық коэфицент деп атайды және оны k ф әрпімен белгілейді. Демек,
к ф =I/I орт =(I m /√2) (2I m /п) =п/2√2 ≈1. 11
3-суретте кешенді сандарды кескіндеуге болатын кешендік жазықтық бейнеленген.
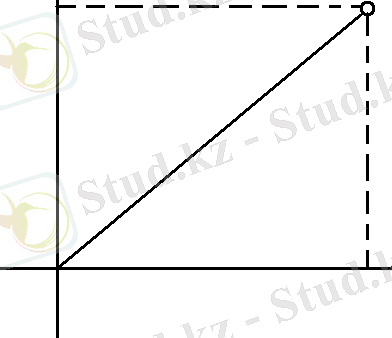
+j
e ja
a
sina
+1
cos a
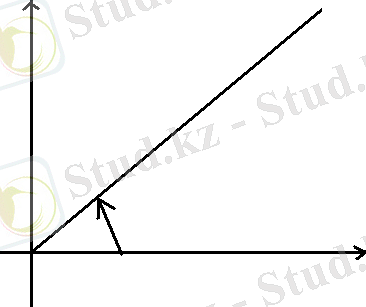
+j I m e j(wt+Ψ)
A=wt+Ψ
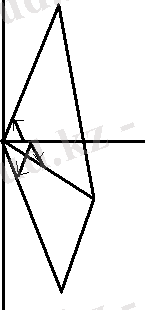
Векторлаық диаграмманың мысалы 5-суретте берілген.
 +j
+j
I im
Ψ
Ψ +1
Ψ
I m
I 2m
Кешендік жазықтықта (4-сурет) i 1 тоғын i 1m = i 1m e jΨ1 - тоғын i 2m = i 2m e jΨ2 векторлары түрінде бейнелеуге болады. (5-сурет)
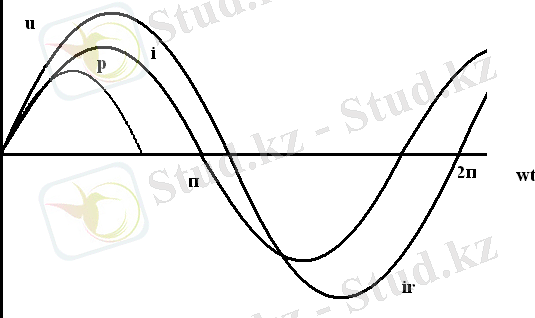
Синусоидалық кернеуді 7а-суретте көруге болады. Кедергінінң қысқыштарындағы кернеудің және токтың бірдей бастапқы фазалары сәйкес келеді деп те айтады, ол 6б-суретте көрсетілген
Синусоидалық ток тізбегіндегі индуктивтілік элемент.
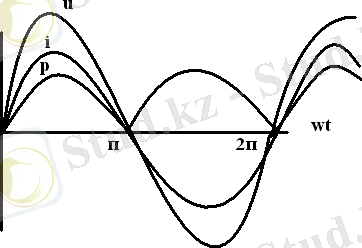
Индуктивтілік элемент уақытқа байланысты магнит ағынының өзгерісінің, ЭҚК-нің туу құбылысының және нақты электр тізбегінің элементінде магнит өрісінің жинақталу құбылысын есептеуге мүмкіндік береді. Оны Ψ-ағындық ілнісуінің і-токтан тәуелділігі (вебер-аперлік сипаттамасы) немесе L=Ψ/I - индуктивтігі сипаттайды. Электрлік схемада индуктивтік элементі 7а-суретіндегідей бейнеленеді. Нақты индуктивтік катушканы схемада ауыстырғанды, және резисторлық элементтер түрінде көрсетуге болады. (7в-сурет)
Енді индуктивтік элементті бөліп алайық (7а-сурет) Онда ол арқылы өтетін і-тоғының, өздік индукциясының ЭҚК-і е L =-Ldi/dt=- LI m cos t =LI m sin t(t - 90 0 ) 7 енді а және b - нүктелерінің арасындағы потенциалдар айырымын анықтайық. Суреттегі b - нүктелесінен а - нүктесіне қарай қозғалған кезімізде, біз е L - ЭҚК - не қарай жүреміз, сондықтан Ψ а = Ψ b +e L ; және U ab = а - Ψ b = Ldi/dt. Бұдан әрі индуктивтк элементтегі кернеуді и L табамы; оны жай әшейін индекссіз и әрпімен белгілейміз, сонда
U ab = U L = U=-e L .
7 сурет 8 сурет
u=wLI m =sin(wt+90 0 ) = U m sin(wt+90 0 ) ;
Мұндағы L - көбейтіндісін X L - мен белгілейді және оны индуктивтік кедергідеп атайды. Ол Оммен өлшенеді:
X L =wL
Осыдан біз ток пен кернеудің әсерлік мәндеріне тиісті амплитудалар, Ом заңынаұқсас екенін, мысалы мынадай қатынаста болатынын көреміз:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz