Анықталған интегралды жуықтап есептеу әдістері (тікбұрыш, трапеция, Симпсон) және олардың Pascal тілінде бағдарламалануы мен қателіктерін талдау


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:
ЖОСПАР
Кіріспе
І. ТАРАУ. АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ЖУЫҚТАП ШЕШУ ӘДІСТЕРІ
1. 1 Анықталған интеграл ұғымы
1. 2 Тікбұрыштар әдісі
1. 3 Трапеция әдісі
1. 4 Симпсон әдісі
ІІ-ТАРАУ АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ЖУЫҚТАП ШЕШУ ӘДІСТЕРІН БАҒДАРЛАМАЛАУ
2. 1 Pascal программалау тілін пайдалану
2. 2 Тікбұрыш әдісін бағдарламау
2. 3 Трапеция әдісін бағдарламау
2. 4 Симпсон әдісін бағдарламау
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР
ҚОСЫМША
КІРІСПЕ
Дербес ЭЕМ-нің кең таралуы және жер-жерлерде компьютерлік сауаттылықтың дамуы ЭЕМ-де есептеулердің түрліше әдістерінің мақсаты мен механизмін жеңілірек қабылдауға да көмектеседі. Білім беру тәжірибесі көрсеткендей көптеген математикалық емес мамандықтардағы студенттер өздерінің қазіргі және болашақтағы іскерлік жұмыстарында ЭЕМ - ді және де программалау тілдерін, түрлерін, әдістерін қолданып келеді.
Жалпы ЭЕМ - ді қолдана отырып көптеген математикалық есептер шешілуде. Соның бірі математиканың бір бөлімі анықталған интеграл тақырыбын жуықтап есептеудегі шешімдерді бағдарламалау тілі арқылы табуды қарастырып отырмыз. Бағдарламалау тілі ретінде Паскаль құрылымдық тілін алып отырмыз.
Неліктен Паскаль программалау тілі алынды?
Паскаль тілі Алгол, Фортрон, Бейсик және басқа құрылымдық программалау тілдермен салыстырғанда әлдеқайда жетілдірілген. Ол құрылымдық программаларды және күрделі есептеулерді құруға мүмкіндік береді. Сондай-ақ мектеп информатика курсында негізгі оқытылатын бағдарламалау тілі болып табылады.
Жазық фигуралардың ауданын жуықтап есептеуде үшбұрыш, төртбұрыш, трапеция, дөңгелек және т. б. жазық фигуралардың ауданын табуға арналған формулалар бар. Және біз бұл білімімізді күнделікті тұрмысымызда пайдаланып та жүрміз. Алайда өмірде аталған фигуралар түрінде емес, кез-келген қисықпен шектелген, еркін формадағы фигуралардың да ауданын табу қажеттігі жиі туады. Ал мұндай есептерді шешуде анықталған интеграл ұғымына, оның геометриялық мағынасына, сондай-ақ оның мәнін қалай есептеуге болатынына тоқталамыз.
Жұмыстың мақсаты : Анықталған интегралды жуықтап шешудің бірнеше әдістерін салыстыра отырып бағдарламалау, қателіктерді анықтау.
Зерттеу нысаны : Pascal бағдарламалау тілін пайдалана отырып, анықталған интегралды жуықтап шешу әдістері: Трапеция, тікбұрыш, Симпсон әдістерінің бағдарламасын түзу.
Дипломның құрылымы : Кіріспеден, 2 тараудан, қорытынды және қолданылған әдебиеттерден тұрады.
І. ТАРАУ. АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ЖУЫҚТАП ШЕШУ ӘДІСТЕРІ
1. 1 Анықталған интеграл ұғымы
Анықталған интеграл және оның қасиеттері. Геометриялық және физикалық есептер.
І-есеп. [a, b] кесіндісінде (a мен b-арқылы сандар) үзіліссіз f(x) ≥ 0 функциясы берілсін. y=f(x) қисығы, Ох өсі және x=a мен x=b түзулерімен шенелген фигураның
- S аудан ұғымын анықтау керек; 2) осы S ауданды табу керек.
Есептегі көрсетілген фигураны қисық сызықты трапеция дейді. Бұл есепті шығару үшін келесі амалды орындаймыз
а)
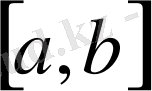 кесіндіні кез-келген a=x
0
<x
1
<x
2
<…. . <x
n
=b нүктелерімен n бөлікке бөлеміз.
кесіндіні кез-келген a=x
0
<x
1
<x
2
<…. . <x
n
=b нүктелерімен n бөлікке бөлеміз.
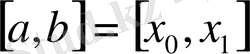
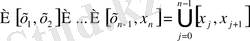 және
және
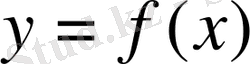 қисығының
қисығының
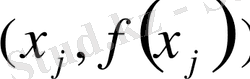 j=0, 1, 2…. ., n
нүктелерінің
j=0, 1, 2…. ., n
нүктелерінің
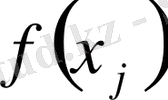 ординаталарын тұрғызамыз;
ординаталарын тұрғызамыз;
б) әрбір
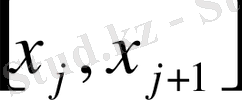 бөлікше кесіндіден кез-келген
бөлікше кесіндіден кез-келген
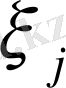 нүктесін
нүктесін
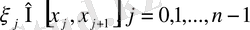 аламыз және осы нүктелердегі
аламыз және осы нүктелердегі
 функция мәндерін тауып, келесі қосындыны құрамыз
функция мәндерін тауып, келесі қосындыны құрамыз
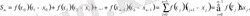
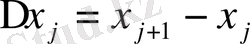
Анықталған өрнек
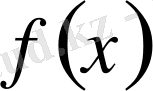 функциясының
функциясының
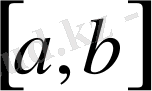 кесіндідегі
интегралдық қосындысы
деп аталады. Оның әрбір
кесіндідегі
интегралдық қосындысы
деп аталады. Оның әрбір
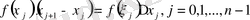 қосылғышы - табаны
қосылғышы - табаны
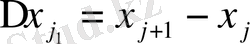 , биіктігі
, биіктігі
 болатын тік төрбұрыш ауданына тең, ал
S
n
саны қисықсызықты трапеция ауданын белгілі бір дәлдікпен жуықтайды:
S
n
≈
S
. Бұл жуық теңдік дәлірек болуы үшін барлық
болатын тік төрбұрыш ауданына тең, ал
S
n
саны қисықсызықты трапеция ауданын белгілі бір дәлдікпен жуықтайды:
S
n
≈
S
. Бұл жуық теңдік дәлірек болуы үшін барлық
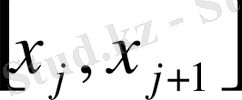 ,
j=0, 1, 2…. ., n-1
, бөлікше кесінділеді мейлінше ұсақтай түсу керек екені түсінікті;
,
j=0, 1, 2…. ., n-1
, бөлікше кесінділеді мейлінше ұсақтай түсу керек екені түсінікті;
в) ұзындығы ең үлкен бөлікше кесіндіні нөлге ұмтылдырамыз
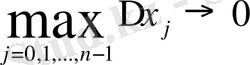
Егерде осыдан
S
n
шамасы
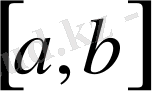 кесіндісін
бөлу тәсіліне
және жәбір бөлікше кесінділерден алынған
кесіндісін
бөлу тәсіліне
және жәбір бөлікше кесінділерден алынған
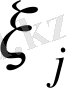 нүктелерін
таңдау тәсілдеріне
тәуелсіз
S
нақты санына ұмтылса, онда
S
саны қисықсызықты трапецияның
ауданы
деп аталады
нүктелерін
таңдау тәсілдеріне
тәуелсіз
S
нақты санына ұмтылса, онда
S
саны қисықсызықты трапецияның
ауданы
деп аталады
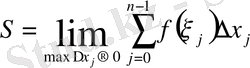 (1)
(1)
Сонымен, І-есептің екі сұрағына да жауап алдық.
ІІ-есеп.
Х
өсіндегі
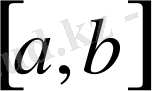 кесіндісінде жатқан сызықтық біртексіз стержень (желі) берілсін. Оның массасының үлестіру тығыздығы ρ(x) -үзіліссіз функция болсын. Осы стерженнің массасын анықтау керек.
кесіндісінде жатқан сызықтық біртексіз стержень (желі) берілсін. Оның массасының үлестіру тығыздығы ρ(x) -үзіліссіз функция болсын. Осы стерженнің массасын анықтау керек.
А) стерженді кез-келген a=x
0
<x
1
<…, <x
n
=b нүктелермен n бөлікке бөліктейміз:
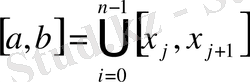 ;
;
Б) әрбір
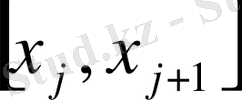 бөліктен кез-келген
бөліктен кез-келген
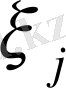 нүктесін
нүктесін
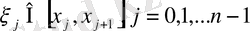 алып, келесі интегралдық қосындысын құраймыз:
алып, келесі интегралдық қосындысын құраймыз:
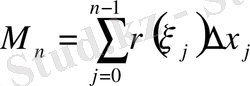
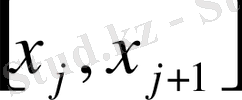 Аралығында ρ(x) функцияның өзгеруі шамалы болғандықтан, стерженнің
Аралығында ρ(x) функцияның өзгеруі шамалы болғандықтан, стерженнің
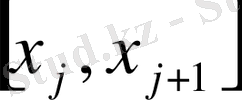 кесіндісіне сәйкес келетін бөлігінің массасының жуық мәні
кесіндісіне сәйкес келетін бөлігінің массасының жуық мәні
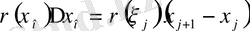 тең болғандықтан, қосындысы M
n
бүкіл стерженнің массасын жуықтайды;
тең болғандықтан, қосындысы M
n
бүкіл стерженнің массасын жуықтайды;
В) стерженнің массасының дәл мәнін, ұзындығын ең үлкен бөлікше кесіндіні нөлге ұмтылдыра отырып, M n интегралдық қосындының шегіне өту арқылы аламыз:
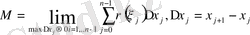
Осы сияқты
f
күшінің әсерінен дененің түзу сызықпен
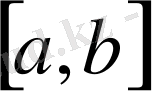 аралығындағы қозғалысының A жұмысын анықтауға болады:
аралығындағы қозғалысының A жұмысын анықтауға болады:
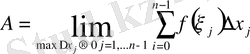
тағы да басқа көптеген физикалық есептерді осылай шешуге болады.
Бұл есептер бізді
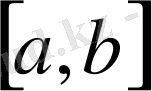 кесіндісінде берілген, тегі әртүрлі функцияларға жасалатын бір ғана математиокалық амалға алып келіп отыр. Бұл амал-функцияны кесіндіде интегралдау деп, ал оның нәтижесі - функцияның кесіндідегі анықталған интегралы деп аталады.
кесіндісінде берілген, тегі әртүрлі функцияларға жасалатын бір ғана математиокалық амалға алып келіп отыр. Бұл амал-функцияны кесіндіде интегралдау деп, ал оның нәтижесі - функцияның кесіндідегі анықталған интегралы деп аталады.
АНЫҚТАМА.
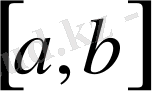 kесіндісінде
y=f(x)
функциясы берілсін.
kесіндісінде
y=f(x)
функциясы берілсін.
А)
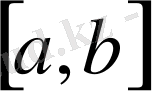 кесіндісін кез-келген a=x
0
<x
1
<…, <x
n
=b нүктелермен
кесіндісін кез-келген a=x
0
<x
1
<…, <x
n
=b нүктелермен
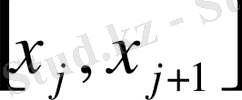 ,
i=0, 1…n-1
, бөліктерге бөлеміз.
,
i=0, 1…n-1
, бөліктерге бөлеміз.
Б) әрбір
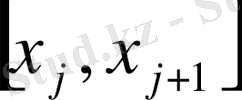 бөліктен кез-келген
бөліктен кез-келген
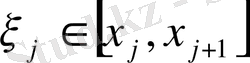 нүктелерін алып,
f
функциясының R-бөліктеуіне сәйкес интегралдық қосынды деп аталатын
нүктелерін алып,
f
функциясының R-бөліктеуіне сәйкес интегралдық қосынды деп аталатын
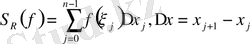
Қосындысын қарастырамыз;
В)
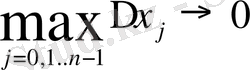 ұмтылдырып интегралдық қосындының шегін аламыз.
ұмтылдырып интегралдық қосындының шегін аламыз.
Егер бұл шек бар болса, онда ол
f
функцияның
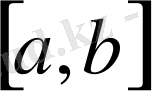 кесіндісіндегі анықталған интегралы деп аталады да
кесіндісіндегі анықталған интегралы деп аталады да
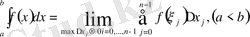 түрінде беріленеді. Мұндағы a мен b сандары - анықталдған интегралдың сәкес
төменгі
және
жоғарғы шегі
деп аталады.
түрінде беріленеді. Мұндағы a мен b сандары - анықталдған интегралдың сәкес
төменгі
және
жоғарғы шегі
деп аталады.
Функцияны интегралдаудың сандық әдістері анықталған интегралдың геометриялық берілуіне, яғни y=f(x) функция графигі абсцисса өсімен және x=a, x=b екі түзуімен шектелген қисық сызықты трапеция ауданына негізделеді:
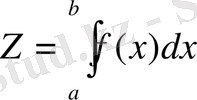
.
Жоғарыдағы қисық сызықты трапецияның ауданын есептеу үшін оларды бірнеше элементар ауданға (қисық сызықты трапеция, трапеция және тікбұрыш) бөлеміз.
1. 2 Тікбұрыштар әдісі
Мынадай жағдайларда кездесуі мүмкін, соңғы түрде табылатын интегралдар үшін жуықтап интегралдау формулаларын қолдану керек болады, бірақ олардың айтылуы қыйынға соғады. Кесте ретінде берілген, құрамында функциялары бар, есептерді шешу кезінде жуықтап интегралдау функциялары әсіресе маңызды болады.
Сандық интегралдауда трапеция және тікбұрыштардың формулалары көбінесе оңай формулалар болып табылады.
Қисық сызықтың көлемін білдіретін, олардың нәтижесі нақты бір интегралдың геометриялық мағынасын қолдануында негізделеді. Кейбір қосымша ұсыныстардан құралған, тікбұрыштардың формуласын интегралдық қосынды деуге болады.
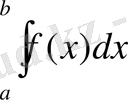 интегралын шығару керек делік,
интегралын шығару керек делік,
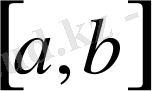 интегралдаудың үзіндісін n бірдей бөліктерге бөліп және функция мағыналары интегралдың қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a) /n бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен қатар мынадай жуық теңдеулер аламыз:
интегралдаудың үзіндісін n бірдей бөліктерге бөліп және функция мағыналары интегралдың қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a) /n бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен қатар мынадай жуық теңдеулер аламыз:
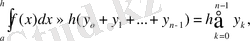 (2)
(2)
Мұнда теріс тікбұрыштардың формуласы деп аталады. Осы жерде бұрынғыдай у 0 , у 1 , у 2 , . . . у n арқылы х 0 , х 1 , х 2 , . . . х n бөлулердің нүктелерінде y=f(x) функцияның мағыналары белгіленген. Тікбұрыштардың ұқсас формуласы былай да шығарылады: егер интегралдық қосындының функция мағыналарын теріс жақта емес, керісінше, бөлулердің оң жақтан алатын болсақ, сол кезде формула осындай болады:
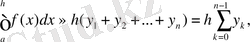 (3)
(3)
Функция үшін, әр интегралдың қосындысы нақты интегралдың (2) және (3) формулалардың оң жақтарында көрсетілген. Жуықталған мағыналардың арасында қосылған. Сол фактінің геметриялық көркемдеуін 1-суреттен көруге болады.
осы жерден әр түрлі қосындыға кіретін, көбеюші функцияны және қосылғандарды алу, пункттер және штрих түсірумен көрстілген.
Осыған орай тікбұрыштардың формулаларының қателіктері туралы көріністі, (2) және (3) формулалары бойынша алынған айырымның нәтижелерін қарастыра білуге болады.
Егер функция интегралдаудың үзіндісінде ақырғы түрде табылатын экстримумдардың санын иеленсе, интегралдаудың үзінділерін бірқалыптылық бөліктерін бөлуге болады. Осылайша тікбұраштар формулаларының қателіктеріне бағалады.
1. 3 Трапеция әдісі
Байқасақ, тіктөртбұрыштардың формуласымен алынған арифметикалық ортасының жуығы қандай да мәнге тең, демек интеграл мағынасының түп мәніне тең болып шығады: қателік 0, 05% -ке тең. (2) және (3) формулалары бойынша алынған, интегралдаудың жуықталған мағынасы ретінде орташа арифметикалықтың жуықтаын алуға тура келеді.
Байқасақ, бұл мағыналарды алдын ала шығарып қоюды еш мұхтаждығы жоқ. Өйткені бірден дайын формуламен пайдаланса болады. Шынымен де, (2) және (3) оң формулаларының арифметикалықтың ортасын алсақ, мынаны аламыз:
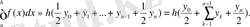 (4)
(4)
бұл трапециялар формуласы.
(4) трапециялар формуласын былайша оңай алуға да болады, геометриялық мағынасынан шыға тура, a=x 0 <x 1 <x 2 <…<x n-1 <xn=b нүктелермен интегралдаудың үзіндісін n-бірдей бөлікке бөліп, бөлулердің барлық нүктелердің ординаталарды жүргіземіз және әр алынған қисық сызықтытыны түзу сызықтыға ауыстырамыз, төмендегі суретте көрсетілген. Әр трапецияның жақтары екі көрші ординаттар болып табылады. Ох сызбаның аймағы, ұзындығы h=(b-a) /n және хордасы қисық.
Сол трапецияның көлемі
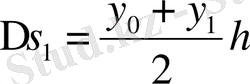 (х
і-1
, х
і
)
(х
і-1
, х
і
)
Аймақтың үстінде орналасқан, трапецияға сай, мынаны табамыз.
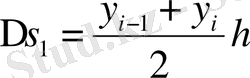 (5)
(5)
1-ден n-ге дейін барлық і-ға (5) көрсетілімдерді қосу, өйткені шеттегіден басқа барлық ординаттар, (5) көрсетілімдердің түрінде екі мәрте қолданылады.
Трапециялық тәсілмен жасалатын сандық интегралдау
ЭЕМ-дағы сандық интегралдау тәсілдерді іске асыруды қажет ететін, нақты бір интегралдың мысалдарын келтірейік.
Мысалы, егерде f(x) - болса, квт-уақытта (х-тәуліктің басынан есептелетін, уақыттың саны), тәуліктің ішінде электірлік энергиялық шығыны құрайтын мынау:
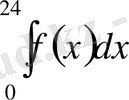 (6)
(6)
немесе басқа мысал:
t-уақытта алынған, дисконтталған кірістің көлемі мынаған тең:
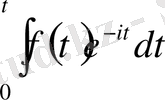 (7)
(7)
осы жерде:
t-уақыт
і-пайыздың меншікті нормасы (пайыздар үздіксіз өсе береді)
Сонымен, математикалық тілмен айтқанда нақты бір интегралды жоғарыдағы формулаларды «санға жеткізу» керек.
Сол үшін осы тақырыпта трапециялық тәсілді қолданамыз.
Тәсілдің мәні: интегралдаудың арасы [a, b] n нүктелермен бірнешеге бөлінеді. (n+1) бірдей кішкентай бөліктерге.
Трапеция формуласының көрінісі:
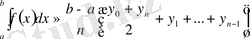 (8)
(8)
f(x) - интегралдың астындағы функциясы;
a, b - интегралдаудың шегі;
n - аралықтың саны;
y i - і нүктеде бөлінетін f(x i ) мағынасы
1. 4 Симпсон әдісі
Сандық интегралдың бұл тәсілінде нақты бір интегралдың түрі қарастырылады (4) :
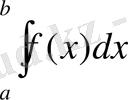
[a, b] интегралдаудың интервалын жұп сан аралығына бөледі демек 2m- ге, демек бөлінетін нүктенің саны 2m+1 -ге тең.
Тәсілдің мәні: Трапецияның тәсіліне қарағанда, Симпсон тәсілінде (x 0 , x 1 ) және (x 1 , x 2 ) екі көрші аралығында және f(x) қисығын (демек интегралдың астындағы функцияны) параболамен ауыстырады, демек алгебралық көпмүшеліктің түрімен
y=f(x) =A(x- x 0 ) (x- x 1 ) +B(x- x 0 ) (x- x 2 ) +C(x- x 1 ) (x- x 2 ) ( 9 )
осы жерде А, В, С- анықтау керек шама
А, В және С анықталғаннан кейін, парабола формуласының немесе былайша айтқанда Симпсон формуласының берілгені мынау:
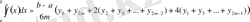
осы жерде y i -0, 1, 2, . . . , 2m бөлінген нүктелердегі f(x) интегралдың астындағы функцияларының мағынасы.
Жоғарыдағы қарастырылған трапеция формуласынан да дәлірек формула Симпсон формуласы деп те аталады. Дәл сондай дәлдікке қол жеткізу үшін бұл формулада бөліну аймағының n санын азырақ алып және сәйкесінше үлкен арақашықтық h -деп алу керек. Бірдей арақашықтарда, яғни дәл сондай шешімнің көлемінде, бұл формулада абсолютті және салыстырмалы қателік жіберіледі.
Симпсон формуласын осы уақытқа дейін екі рет қолданған тәсілмен алуға болады.
Аумақты
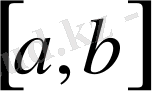 жұп санды n=2m бөлікке нүктелермен бөлеміз a= x
0
< x
1
<…< x
n-1
< x
n
=b, ординаттарды бөліну нүктелерінде y
0
, y
1
, … y
n
арқылы белгілейміз де, көршілес аумақтардың бір-екеуін қарастырамыз. Мысалы, шеткі сол жақтағы a= x
0
нүктені қарастырайық.
жұп санды n=2m бөлікке нүктелермен бөлеміз a= x
0
< x
1
<…< x
n-1
< x
n
=b, ординаттарды бөліну нүктелерінде y
0
, y
1
, … y
n
арқылы белгілейміз де, көршілес аумақтардың бір-екеуін қарастырамыз. Мысалы, шеткі сол жақтағы a= x
0
нүктені қарастырайық.
Үш нүкте арқылы қисық сызықты координаталармен параболаны (x 0 у 0 ), ( x 1 у 1 ), ( x 2 у 2 ) өсімен бірге жүргіземіз. Бұл ось О у параллель болу керек. Оның теңдеуі былай болады:
y= Ах 2 +Вх+С (10)
бірақ А, В, С коэффенцентері әзірше белгісіз болып қала береді:
[x 0 , x 2 ] аумағында берілген қисық сызықты трапецияның ауданын (1, 3, 1) параболамен шектелген қисық сызықты трапецияның ауданымен алмастырып, жақындатылған теңдікке келеміз:
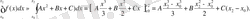
жақшаның сыртына жалпы көбейткіштерді x 2 - x 0 шығарып, содан кейін жалпы бөлгішке әкелемі де, мынадай формуланы аламыз:
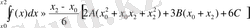 (11)
(11)
(10) теңдеуіндегі және (11) формуласындағы белгісіз А, В, С коэффенценттері x
0,
x
1,
x
2
-ге тең х мағынасындағы жағдайдан табылады. F(x) функциясы жағдйында сәйкес мағынаға ие болады.
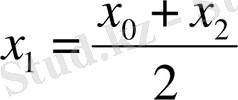 екендігін байқасақ, бұл жағдайларды мына түрде жазамыз:
екендігін байқасақ, бұл жағдайларды мына түрде жазамыз:
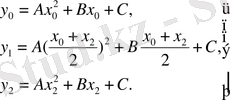 (12)
(12)
Екінші теңдікті (12) төртке көбейту арқылы және содан кейін үш теңдікті қатарластыру арқылы мынаны аламыз:
y 0 +4 y 1 + y 2 =A[x 0 2 + ( x 0 + x 2 ) 2 + x 2 2 ] +B[x 0 +2(x 0 + x 2 ) + x 2 ] +6C=2A(x 0 2 + x 0 x 2 + x 2 2 ) +3B(x 0 + x 2 ) +6C (13)
(13) теңдеудің оң бөлігінде төрт бұрышты жақшамен сәйес келеді.
(15) -ті (13) теңдеудің оң бөліміне қоя тұра, x 2 -x 0 =2h ескеріп, жуықталған теңдеуге келеміз
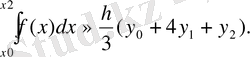 (14)
(14)
Әр ендігі бөлікке тура сондай формула келетіні анық:
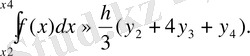 (15)
(15)
(15) және (16) теңдеулердің көрінісін барлық аймақ бойынша қоса тұра, мынадай формула аламыз: (17)
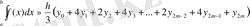
(17) формуласы бізге керек болған Симпсон формуласы. Формуланың геометриялық мәнін ескере тұра, оны парабола формуласы деп те атайды. Онда барлық ординаттар тақ нөмірмен төртке көбейтіледі, жұп санмен екіге. у 0 және у 2m шеткі ординаттар коэффенценттері бар формулаға кіреді, олар бірге тең.
ІІ-ТАРАУ АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ЖУЫҚТАП ШЕШУ ӘДІСТЕРІН БАҒДАРЛАМАЛАУ
2. 1 Pascal программалау тілін пайдалану
Паскаль тілі Алгол, Фортрон, Бейсик және т. б. әмбебеп программалау тілдермен салыстырғанда әлдеқайда жетілдірілген. Ол құрылымдық программаларды және күрделі есептеулерді құруға мүмкіндік береді.
Паскальда ішкі программаларда (процедуралар және функциялар) алдынғы қатарлы және тиімді программалау әдістерінің бірі құрылымдық программалауды қолдануға мүмкіндік береді.
Сондай-ақ, Паскаль қарапайым және ақылға қонымды, адамның табиғи тіліне айтарлықтай жақындатылған. Осы жағдай оны түсінуді және үйренуді жеңілдетеді.
Паскаль-программасының жалпы құрылымы:
{программаның сипатау бөлігі }
Program < аты >
Label белгілер бөлімі
Const констант бөлімі
Type типтер бөлімі
Var айнымалыны сипаттау бөлімі
Procedure, function процедура және функция бөлімі
{ программаның атқарушы бөлігі }
Begin
oператор 1;
oператор 2;
. . .
оператор n;
оператор(n+1) ;
End.
Жоғарыда көрсетілген Паскаль программасының құрылымынан көретініміздей, сипаттау бөлігінде дәл осы процедура функция бөлімінің болуы атқарушы бөлікті зерттеуде қолданылатын функия түрінен тәуелсіз етеді. Бұл жағдай Паскаль - программасының әрқайсысын барлық қарастырылған әдістерге қолдануға болатындығын көрсетеді.
Біздің қарастыратын есебімізде Паскаль тіліндегі процедура және функция бөлімі кеңінен қолданылады
2. 2 Тікбұрыш әдісін бағдарламау
Мысал.
[0, 1] аймақты 10 бөлікке бөле тұра, h=0. 1 деп алып,
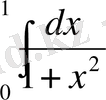 - ді тікбұрыштар тәсілімен шешейік, функция мағыналарының есептері 1, 1 - кестеде берілген:
- ді тікбұрыштар тәсілімен шешейік, функция мағыналарының есептері 1, 1 - кестеде берілген:
0, 0
0, 1
0, 2
0, 3
0, 4
0, 5
0, 6
0, 7
0, 8
0, 9
1, 0
0, 00
0, 01
0, 04
0, 09
0, 16
0, 25
0, 36
0, 49
0, 64
0, 81
1, 00
1, 00
1, 01
1, 04
1, 09
1, 16
1, 25
1, 36
1, 49
1, 64
1, 81
2, 00
1, 000
0, 990 0990
0, 961 5328
0, 917 4312
0, 862 0690
0, 800
0, 735 2941
0, 671 1409
0, 609 7561
0, 552 4862
0, 500
Біріншіде жағдайда (1, 1) және (1, 2) қолданылатын формулалар тауып аламыз:
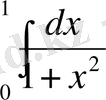 ≈0, 1*(1, 0+0, 9900990+0, 9615385+0, 9174312+0, 8620690+0, 8+0, 7352941+0, 6711409+ +0, 6097561+0, 5524862) =0. 8099815.
≈0, 1*(1, 0+0, 9900990+0, 9615385+0, 9174312+0, 8620690+0, 8+0, 7352941+0, 6711409+ +0, 6097561+0, 5524862) =0. 8099815.
және екіншіден:
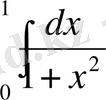 ≈0. 1*(0. 9900990+0. 9615385+0. 9174312+0. 8620690+0. 8+0. 7352941+0. 6711409+ +0. 6097561+0. 5524862+0. 5) =0. 7599815
≈0. 1*(0. 9900990+0. 9615385+0. 9174312+0. 8620690+0. 8+0. 7352941+0. 6711409+ +0. 6097561+0. 5524862+0. 5) =0. 7599815
Теріс тікбұрыштың формуласына арналған алгоритмі және программасы:
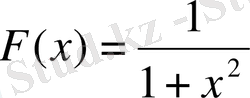
Оң тікбұрыштың формуласына арналған алгоритм және программа:
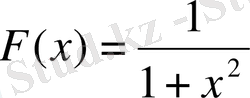
program Lebpr1;
label MM, MM1, MM2;
var x, a, b, eps, h, z, s, s0:real;
n, k:longint;
function f(x:real) :real;
begin
f:=1/(1+sqr(x) )
end;
begin Write('нижний предел=') ; read(a) ;
Write('верхний предел=') ; read(b) ;
Write('число интервалов=') ; read(n) ;
Write('точность=') ; read(eps) ;
z:=1;
MM:s:=0; h:=(b-a) /n;
for k:=1 to n do begin
x:=a+(k-1) *h;
s:=s+f(x) ;
end;
s:=h*s;
writeln('n=', n' s=', s) ;
if z=1 then go to MM1;
if ABS(s0-s) <=eps then go to MM2;
MM1:s0:=s; z:=0; n:=2*n; go to MM;
MM2:end.
Жауабы:n=10
S=7. 5998142723E-01
program prapr1;
label MM, MM1, MM2;
var x, a, b, eps, h, z, s, s0:real;
n, k:longint;
function f(x:real) :real;
begin
f:=1/(1+sqr(x) )
end;
begin Write('нижний предел=') ; read(a) ;
Write('верхний предел=') ; read(b) ;
Write(' число интервалов=') ; read(n) ;
Write('точность=') ; read(eps) ;
z:=1;
MM:s:=0; h:=(b-a) /n;
for k:=1 to n do begin
x:=a+k*h;
s:=s+f(x) ;
end;
s:=h*s;
writeln('n=', n' s=', s) ;
if z=1 then goto MM1;
if ABS(s0-s) <=eps then goto MM2;
MM1:s0:=s; z:=0; n:=2*n; goto MM;
MM2:end.
Жауабы:n=10
S=7. 06896458923E-01
2. 3 Трапеция әдісін бағдарламау
Мысал. [0, 1] аумағын 10 бөлікке бөле отырып,
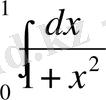 трапециялар тәсілі бойынша шығарайық, демек h=0, 1 қадаммен, функция мағыналарының шешімі 1, 1-кестеде (2, 1) формуласын қолдана отырып табамыз.
трапециялар тәсілі бойынша шығарайық, демек h=0, 1 қадаммен, функция мағыналарының шешімі 1, 1-кестеде (2, 1) формуласын қолдана отырып табамыз.
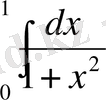 ≈0, 1*(1, 0/2+0, 9900990+0, 9615385+0, 9174312+0, 8620690+0, 8+0, 7352941+0, 6711409 +0, 6097561+0, 5524862+0, 5/2) =0. 7849815.
≈0, 1*(1, 0/2+0, 9900990+0, 9615385+0, 9174312+0, 8620690+0, 8+0, 7352941+0, 6711409 +0, 6097561+0, 5524862+0, 5/2) =0. 7849815.
Трапеция формуласы алгоритм және программа тілдерінде:
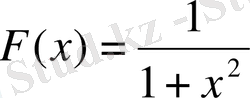
program trap1;
label MM, MM1, MM2;
var x, a, b, eps, h, z, s, s0:real;
n, k:longint;
function f(x:real) :real;
begin
f:=1/(1+sqr(x) )
end;
begin Write('нижний предел=') ; read(a) ;
Write('верхний предел=') ; read(b) ;
Write('число интрвалов=') ; read(n) ;
Write('точность=') ; read(eps) ;
z:=1;
MM:s:=(f(a) +f(b) ) /2; h:=(b-a) /n;
for k:=1 to n-1 do begin
x:=a+k*h;
s:=s+f(x) ;
end;
s:=h*s;
writeln('n=', n' s=', s) ;
if z=1 then goto MM1;
if ABS(s0-s) <=eps then goto MM2;
MM1:s0:=s; z:=0; n:=2*n; goto MM;
MM2:end.
Жауабы:n=10
S=7. 8499149723E-01
Трапеция формуласын іске асыру үшін Паскаль -бағдарламасын құрамыз:
program Trapecia;
const n=4;
type t=array[0. . n] of real;
var x, y:t;
i:integer;
a, b, h, s:real;
function fff(i:integer) :real;
begin
y[i] :=1/x[i] ;
end;
begin
writeln;
writeln;
writeln(' ':20, 'Dobro pogalovat v programmu Trapecia!') ;
read(a, b) ;
s:=0;
h:=(b-a) /n;
for i:=0 to n
do
begin
x[i] :=a+i*h;
fff(i) ;
write(x[i] :5:2) ;
write(y[i] :5:2) ;
writeln;
s:=s+y[i] ;
end;
s:=s-(y[0] +y[n] ) /2;
s:=h*s;
writeln;
writeln(' ':20, 'Znachenie integrala I=', s:5:2)
end.
Трапеция тәсілін іске асыратын TRAPECIA бағдарламасын қолдану құрылымы:
- Интегралдаудың арасын бөлу керек болатын бөліктердің саны, сол санға n-ді теңдетіп, бағдарламаның суреттелетін бөліктің 2-ші қатарында беріледі: қазір n=4 беріліп тұр.
- Интегралдың астындағы функциялардың барлық параметрларын, бағдарламада бар символдарды қолданбай, (і, а, b…) varауыспалы бөлімінде бағдарламаның суреттелетін бөлігінде беру керек.
- Интегралдың астындағы функцианыfff functionфункция бөлімінде бағдарламаның суреттейтін бөлімінде конструкциялау керек; оныbeginжәнеendдеген логикалық жақшалардың арасында істеу керек.
- Енді бағдарламаны орындау керек. Содан кейін компьютер бағдарламаның жұмысына керек, қажет берілгендерді енгізу үшін куту тәртібіне өтеді.
- Бағдарлама экранға мынадай хабарлама шығарады: «интегралдың мағынасы мынаған тең»
Паскаль-TRAPECIA бағдарламасының қолданылу мысалы: интегралдың аралығын төртке бөліп, трапеция тәсілімен интегралдың мағынасын табу:
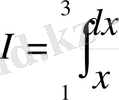 [1, 3] аралығын 4 - бөлікке бөлу арқылы интегралдау.
[1, 3] аралығын 4 - бөлікке бөлу арқылы интегралдау.
Шешімі:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz