Механикалық тербелістер мен тербелмелі жүйелер

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:

Мазмұны

Кіріспе . . . 5

І тарау. Механикалық тербелістер мен тербелмелі жүйелер

1. 1. Гармониялық тербелістер . . . 6

1. 2. Маятниктердің тербелістері . . . 9

1. 3. Бір түзудің бойымен бағытталған тербелістер . . . 15

1. 4. Өзара перпендикуляр тербелістерді қосу . . . 18

1. 5. Өшетін және мәжбүр тербелістер . . . 21

Механикалық тербелістер тарауы

бойынша қайталау сұрақтары мен есептер . . . 28

ІІ тарау. Механикалық тербелістер тақырыбының

тәжірибелерін сандық модельдеу

2. 1. Сандық модельдеу пәні . . . 32

2. 2. Модель ұғымы . . . 34

2. 3. Компьютерлік модельдеуде қолданылған бағдарлама . . . 39

2. 4. Бір түзудің бойымен бағытталған тербелістер . . . 42

2. 5. Өзара перпендикуляр тербелістерді қосу . . .

2. 6. Өшетін тербелістерді сандық модельдеу . . .

Қорытынды . . .

Пайдаланылған әдебиеттер . . .

Кіріспе

Зерттеу жұмысының өзектілігі:

«Тербелістер физикасы» өз алдына физика ғылымының арнаулы бір саласы. Ол табиғатты әр түрлі тербелістер процестерін біріктіріп, бірдей (сандық) заңдылықтар негізінде қарастырады. Компьютерлік технологиялардың дамуы ғылымның барлық саласына септігін тигізуде. Тербелмелі үдерістер күрделі заңдылықтарға бағынатындықтан есептеулерде сандық әдістер көмегіну жүгінуге тура келеді.

Тербелістерді зерттеуге көп үлес қосқан ғалымдар: ағылшындардан-У. Томсон(лорд Кельвин) және Дж. Релей, орыстардан А. С. Попов және П. Н. Лебедев, А. Н. Крылов, Л. И. Мандельштам, Н. Д. Папалекси, Н. Н. Боголюбов, және т. б.

Бағыттары бірдей екі тербелістердің қосылуының, өзара перпендикуляр тербелістерді қосу графигін, техникаларда болатын сызықтық емес тербелістерді сипаттауда компьютерлік модельдеуге жүгінуге тура келеді. Оның көмегімен түрлі маятниктердің, өшетін және мәжбүр тербелістердің қозғалысын сандық модельдеу олардың қозғалыс ерекшеліктерін көрнекілендіруге мүмкіндік аламыз. Бұл мәселені шешуде компьютерлік моделдеу мен есептеуді қолданудың маңызы өте зор. Себебі бұл тақырыптардың механикалық моделін жасау қиын, ал шығатын графигінің күрделілігі компьютерлік есептеуді талап етеді.

Осы бағытта қазіргі таңда жоғары оқу орындарында оқытудың иновациялық әдістері қолданылып келеді. Солардың бірі, оқу үрдісінде жаңа технологияларды, интерактивті әдістер мен компьютерлік технологияларды қолдану болып табылады. Механикалық тербелістер тақырыбының көрнекіленуін ұйымдастыру проблемасы осы дипломдық жұмыстың өзектілігін білдіреді.

Физикадағы тәжірибелерді оңай түсіндіруге мүмкіндік беретін компьютерлік моделдер физиканы оқыту үдерісіндегі жаңа әдістердің бірі болып саналады. Дипломдық жұмыста сол модельдер құрастырылды. Бұл жұмыстар сондай - ақ кейбір қарапайым жағдайларды есептеуге мүмкіндік туғызады.

Бірінші тарауда тербелістердің тәжірибелік негізін, олардың физикалық тұрғыдан түсіндірілуін, қолданылуын, есептелу жолдарын қарастырдық. Сонымен қатар тақырып бойынша ұсынылатын сұрақтар мен жаттығулар қарастырылады.

Екінші тарауда сол жасалған тәжірибелердің компьютердегі жазылуы, суреттері мен алгоритмдік блок сұлбалары мен бағдарламасы енгізілген.

Дипломдық жұмысымыз физиканың компьютерлік әдістері, физика-механикалық үдерістерді сандық модельдеу, информатикдан оимпиадалық есептерді шығаруда қолданыс табады деп есептейміз.

Зерттеу жұмысының нысанасы :

Оқу барысында алған білімдерді пайдалана отырып, бағдарламалау тілдерінде есеп шығару жолдарының кейбір мәселелерін қарастыру. Объектілі бағдарланған бағдарламалау тілдерінде динамикалық модельдер құру мәселесі негізгі нысан болып отыр.

Зерттеу жұмысының мақсаты:

Зерттеу жұмысымның барысында физиканың күрделі тақырыптарының бірі- Механикалық тербелістер мен тербелмелі жүйелердің физикалық заңдылықтары мен бағдарламалау тілдері арасындағы алгоритмдік байланысты қалыптастыру жолдарын ұйымдастыру дипломдық жұмысымның мақсатын анықтайды.

Зерттеудің ғылыми болжамы:

Егер оқыту үдерісінде физикалық құбылыстардың сандық заңдылықтарға бағынатындығы компьютерлік модельдер арқылы көрсетілсе бағдарламалау тілінің басқа пәндерде алатын маңызы мен міндеті айқындалады. Объектілі бағдарланған бағдарламалау тілдерінде жасалған динамикалық модельдер құбылысты толығымен түсіндіреді деп есептелінеді егер оның нәтижесі жалқыдан жалпыға көшкен, яғни барлық жеке жағдайларды қамтитын болса.

І тарау. Механикалық тербелістер мен тербелмелі жүйелер

1. 1. Гармониялық тербелістер

Физикада және техникада қозғалыстардың белгілі бір заңға бағынып, қайталанып тұратын түрлері жиі кездеседі. Мұндай қозғалыстарды тербелмелі қозғалыстар немесе тербелістер деп атайды. Бір секундтағы тебеліс бір тербеліс жиілігі - 1 Герцқа тең, ол адам жүрегінің соғу жиілігіне жуық. Ал «Херц» деген сөз неміс тілінен аударғанда «жүрек» деген сөз екен.

Егер тербеліс кезінде тек қана механикалық шамалар (орын ауыстыру, жылдамдық, үдеу, механикалық энергия және т. б. ) қайталанып тұратын болса, тербелістер механикалық тербелістер деп аталады.

Тербеліс кезінде өзгеретін механикалық шамалардың мәндері бірдей уақыт аралығында қайталанып отырса, тербелісті периодты тербеліс деп аталады. Тербеліс периоды Т деп тербелісті сипаттайтын барлық физикалық шамалардың мәндері қайталану үшін қажетті ең кішкентай уақыт аралығын атайды. Бір периодқа тең уақыт ішінде бір толық тербеліс болады. Тербеліс жиілігі деп бір өлшем уақыт ішіндегі толық тербеліс санымен өлшенетін физиклық шаманы айтады, яғни

Периодтық тербелістердің ең қарапайым түрі гармониялық тербелістер. Гармониялық тербелістер деп синус немесе косинус заңына бағынып өзгеретін тербелістерді айтады.

Мысалы, тербеліп тұрған нүктенің тепе - теңдік жағдайдан шығып, орын ауыстыруы х = Аsin(ωt+φ) заңына бағынып немесе x = Acos(ωt+φ) заңына бағынсын. Бұл жағдайда тербелістің орын ауыстыруы гармониялық орын ауыстыру деп аталады. Сонда ең үлкен орын ауыстыру (ығысу деп аталады) х _max = A, себебі‌ │sin(ωt+φ) │ _max = 1. Ең үлкен ығысу тербеліс амплитудасы деп аталады. Ал, ωt+φ =α шамасы тербеліс фазасы болады. Уақыт санаудың басына сәйкес, яғни t = 0 фаза бастапқы фаза деп аталады.

α = φ Ал, - циклдік жиілік, дөңгелектік жиілік делінеді. Тербеліп тұрған материялық нүктенің жылдамдығы мен үдеуінің өзгеріс заңдарын табу үшін орын ауыстырудың (ығысудың) бірінші және екінші туындыларын табу қажет, яғни

Егер ығысу косинус заңына бағынатын болса, онда ығысу жылдамдығы да косинус заңына бағынады, бірақ фазасы алға озып отырады, ығысу үдеуі ығысуға пропорционал болады, бірақ үдеу векторының бағыты ығысу векторының бағытына қарама - қарсы болады.

Соңғы теңдеуді түрлендіріп жазайық, яғни

Сөйтіп дифференциалдық теңдеуді шығарып аламыз. Бұл теңдеу гармониялық тербелістер теңдеуі деп аталады. Гармониялық тербеліс мынадай графикалық модель арқылы бейнеленеді.

1 - сурет. Гармониялық тербелістің

графикалық моделі.

Сан мәні тербеліс амплитудасына тең векторы бастапқы мезетте горизонтал өстен бастапқы фазаға тең бұрыш жасап, векторы 0 нүктесінен бірқалыпты циклдік жиілікпен айнала бастасын. Сонда уақыт t болатын мезетте ωt бұрышына бұрылып, горизонталь өспен α = ωt = φ бұрыш жасайды. Осы мезеттегі векторының горизонталь өске проекциясы

x = Acosα = Acos(ωt+φ) болып, гармониялық тербелісті сипаттайды. Егер горизонталь емес болса, онда у = Аsin(ωt+φ) заңына бағынатын гармониялық тербеліс алар едік.

Гармониялық тербеліс кезінде 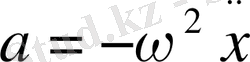тең екені белгілі. Ньютонның екінші заңы бойынша F = ma, олай болса гармониялық тербеліс болу үшін массасы m материялық нүктеге әсер ететін күш F= mω ² x заңына бағынып өзгереді. Яғни тербеліс күші ығысуға пропорционал болу қажет, бірақ күш векторының бағыты ығысу векторының бағытына қарама - қарсы бағытта болуы тиіс. Тек осындай күштер ғана гармониялық тербелістер туғыза алады. Мұндай күштерді серпімділік немесе квазисерпімділік күштері деп атайды. Серпімділік күштері дейтін себебі, серпімділік деформациясы кезінде пайда болатын, Гук заңына бағынатын күштер гармониялық тербелістер тудыра алады. Ал, квазисерпімділік күштері дейтін себебі, кей жағдайларда гармониялық тербеліс тудыратын күштер серпімділік күштері болмағанымен, олардың сыртқы қасиеттері серпімділік күштерге ұқсас болады.

Гармониялық тербелістерге математикалық маятниктің, серіппелі маятниктің, бұрылғыш маятниктің, аударылмалы маятниктің және тағы сол сияқты маятниктердің тербелістері жатады.

1. 2. Маятниктердің тербелістері

Деформацияланбайтын, массасын елемеуге болатын жіпке ілінген материялық нүктенің тепе - теңдік қалпынан шығарған кездегі тербелісі гармониялық тербелісі болады және бұл жүйе математикалық маятник деп аталады. Математикалық маятник гармониялық тербеліске келу үшін квази серпінді күш қалай пайда болады?

2 - сурет. Математикалық маятникті гармониялық тербеліске

келтіретін квазисерпімділік күштің пайда болуы.

Тепе - теңдік қалыпта вертикал сызық бойымен орналассын. Бұл жағдайда маятниктің ауырлық күші және жіптің керілу күші бір сызықтың бойымен орналасын және 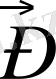+ = 0 маятникті тепе-теңдік қалпынан шығарып, солға қарай α бұрышқа ауытқытайық. Енді жоғарыдағы екі күштің бағыттары басқаша болады: ауырлық күші бұрынғыдай вертикал төмен бағытталған, ол керілу күші жіптің бойымен вертикалға α бұрыш жасап іліну нүктесіне қарай бағытталған.

Бұл екі күштің геометриялық қосындысы, қорытқы күш 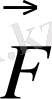тепе - теңдік қалпынан ығысу векторы мен күш векторының бағыттары қарама - қарсы екенін көреміз. Ығысу бұрышы кішкентай болса, доға мен хорданың сан мәндерінің айырмасы жоқ деп қарауға болады, яғни ығысу доғасының орнына ығысу хордасы алынады. Ығысу хордасын Х деп белгілейік. Ығысу хордасы маятник үшін тепе - теңдік қалпынан ығысу болып табылады. Қорытқы күш ( ) пен ығысу (Х) арасындағы тәуелділікті табайық. Қорытқы күш ( 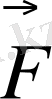) жанаманың бойымен бағытталғандықтан F = P sin α = mg sin α тең. Ауытқу бұрышы кішкентай болса, sin α = α, онда F = mg α. Екінші жағынан

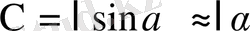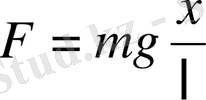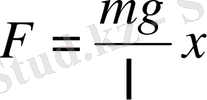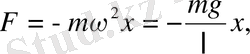. Сонда . Ығысу векторы күш векторына қарама - қарсы екенін ескерсек, онда . Бұдан қорытқы күштің ығысуға пропорционал екенін көруге болады, себебі m, g және - тұрақты шамалар. Сондықтан математикалық маятниктің тербелісі квазисерпімділік күштің әсерінен гармониялық тербеліс болады. Енді тербеліс периодын табалық. Квазисеріпінділік күштің цикілдік жиіліктің тең екенін ескерсек, сонда тербеліс периоды

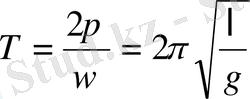
Математикалық маятниктің периоды маятник ұзындығының квадрат түбіріне тура пропорционал да, маятник тұрған жердегі еркін түсу үдеуінің квадрат түбіріне кері пропорционал болады.

Серіппелі маятник деп вертикал орналасқан серіппеге іліеген жүктің тұратын жүйені айтамыз.

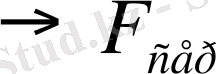
2- сурет. Серіппелі маятникте пайда болатын серпімділік күші.

Тепе-теңдік қалыпта ілінген жүктің ауырлық күші созылған серіппеде пайда болатын серпінділік күшімен теңеседі. Егер жүк тепе-теңдік қалпынан төмен қарай ауытқыса, серіппе ішінде Гук заңына сәйкес күші пайда болады, мұндағы К- серіппенің серпінділік коэффициенті, серпінділігі қаттылығы деп аталады. Енді серіппелі маятниктің тербеліс периодын табалық. Квазисеіпінділік күштің 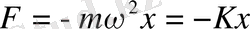цикілдік жиіліктің - 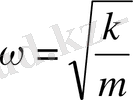тең екені белгілі, сонда тербеліс периоды .

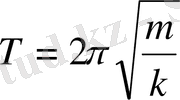Серіппелі маятниктің тербеліс периоды тербелетін дененің массасының квадрат түбіріне тура пропорционал да, серіппенің қаттылығының квадрат түбіріне кері пропорционал.

Математикалық маятник үшін қорытқы күш 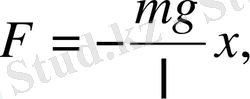ал серіппелі маятник үшін серпімділік күші екенін білеміз. Сонда шамасы серпімділік коэффициентінің рөлін атқарып тұр. Бұл шаманы квазисерпінділік коэффициенті деп қарауға болады. Сөйтіп серпінділік немесе квазисерпінділік күштерін бір ғана формула арқылы беруге болады. 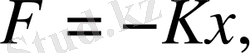мұндағы F-серпінділік немесе квазисерпінділік коэффициенті, Х - жүйенің тепе-теңдік қалпынан ығысуы. Кез-келген серпінділік немес еквазисерпінділік күштердің әсерінен тербелетін жүйенің тербеліс периодының формуласы. 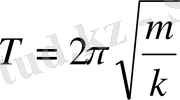арқылы табылады, мұндағы m - жүйенің массасы, k - серпінділік немесе квазисерпінділік коэффициенті. 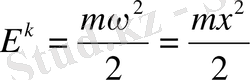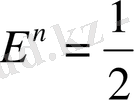Тербеліп тұрған дененің кинетикалық энергиясы потенциалдық энергиясы 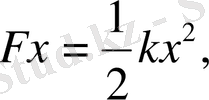ал толық энергиясы, механикалық энергиясы ,

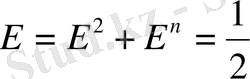Тербеліс гармониялық болса, 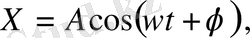онда ығысу жылдамдығы 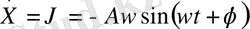тең болады. Олай болса жүйенің механикалық энергиясы 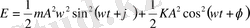және 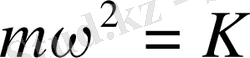тең екенін ескерсек онда

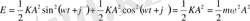тең болады.

Гармониялық тербеліс жасайтын жүйенің механикалық энергиясы уақыттан тәуелді емес және ол тұрақты шама.

Бұл тұжырымдама механикалық энергияның тербелмелі қозғалыс үшін сақталуының дербес жағдайы болып табылады.

Маятниктердің жалпы түрі - физикалық маятник. Физикалық маятник деп қозғалмайтын горизантал өстен айнала тербеле алатын етіп ілінген, тірелген кез келген қатты денені айтады.

3-сурет. Физикалық маятник

Горизантал О өсінен еркін айналатын қылып істелінген қатты денені вертикал тепе-теңдік қалпынан φ бұрышқа бұрайық. Физикалық маятниктің ауырлық центірі С нүктесі болсын, іліну өсінен ауырлық центіріне дейінгі қашықтықты а әрпімен белгілейік. Дененің тепе-теңдік қалпынан ауытқыған кездегі пайда болатын потенциалдық энергия.

Ауытқу бұрышы кішкентай болса, онда сондықтан 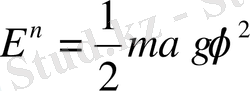тең болады. Жалпы формула бойынша мұндағы К - серпінділік коэффициенті, Х - дененің тепе-теңдік қалпынан ығысу. Біздің жағдайда ығысу бұрышы алынып тұр. Олай болса

Енді тербелетін физикалық маятниктің кинетикалық энергиясының формуласын қарастыралық. Кинетикалық энергия 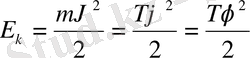мұнда массаның рөлін инерция моменті атқарады. Сондықтан, физикалық маятниктің тербеліс периоды 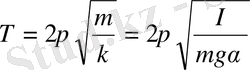тең болады.

Физикалық маятниктің тербеліс периоды оның инерция моментінің квадрат түбіріне тура пропорционалда, массасымен ауырлық центіріне дейінгі қашықтық пен еркін түсу үдеуінің көбейтіндісінің квадрат түбіріне кері пропорционал болады.

Егер маятник математикалық болса, онда 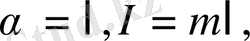олай болса

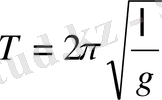
Физикалық маятникпен қатар ілінген математикалық маятниктің тербеліс периодтары бірдей болу үшін 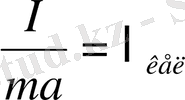шарты орындалуы қажет.

Тербеліс периоды берілген физикалық маятниктің тербеліс периодына тең болатынын математикалық маятниктің ұзындығы физикалық маятниктің келтірілген ұзындығы деп аталады. Келтірілген ұзындыққа сәйкес нүктелер - О және яғни ОО ₁ =l _кел . Егер физикалық маятникті О нүктесінен босатып, О ₁ нүктесінен іліп, қойсақ онда оның тербеліс периоды өзгермейді. Кез-келген маятник үшін l _кел >a шарты орындалуы қажет. Себебі Штейнер теориясы бойынш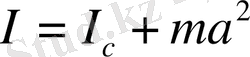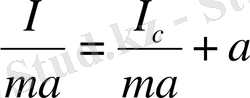а , сонда

Іліну нүктесімен келтірілу нүктесі (тербелу центірі деп те аталады) өзара алмасуға мүмкіндік жасалған физикалық маятник аударылмалы маятник деп аталады.

4-сурет. Аудармалы маятник. 5-сурет. Бұралғыш маятник.

Болат шыбықтың екі ұшында маятниктің тербелісін туғызатын тіреуіш үшбұрышты призмалар (А және В) орналасқан. Жүйенің ауырлық центірі С нүктесінен төменірек В тетігі бекітілген. Сол сияқты Д тетігі суретте А тіреуіш призмасының жоғарғы жағында орналасқан және оны шыбықтың бойымен жылжытып отыруға мүмкіндік болуы қажет.

Әуелі іліну нүктесі ретінде А нүктесі алынады да, жүйенің тербеліс периоды анықталады.

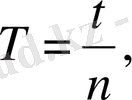мұндағы n - тербеліс саны, t - тербеліс уақыты. Сонан кейін маятник аударылып, іліну нүктесі ретінде А нүктесі алынады. Сонда тербеліс периодының шамасы өзгереді. В тетігін жылжыту арқылы тербеліс периоды бірінші жағдайдағы мәнге тең болатындай етуге болады. Сонда 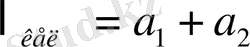тең болады. Аудармалы маятникті еркін түсу үдеуін анықтау үшін қолданылады.

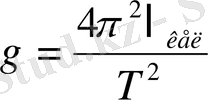
Маятниктің келесі түрі - бұралғыш маятник (5-сурет) . Бұралғыш маятник деп жоғарғы ұшы бекітілген ұзын шыбықтың екінші ұшына бұралатын етіп қондырылған денені айтады.

Бұралғыш маятниктің кинетикалық энергиясы 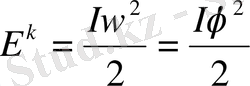тең болады. Мұнда массаның рөлін энерция моменті атқарады. Ал, потенциалдық энергияс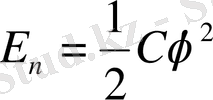ы тең болады. Мұндағы φ - бұрылу бұрышы, С ² - бұрылудың серпінділік коэффициенті. Шыбыққа байланысты бұрылу бұрышы 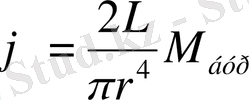формуласы бойынша 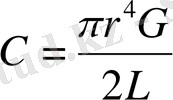болады. Бұралғыш маятниктің тербеліс периоды 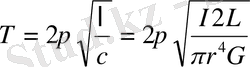формуласы арқылы табылады.

1. 3 Бір түзудің бойымен бағытталған тербелістер

Бір дене екі тербеліске қатынасатын жағдайлар жие кездеседі. Біз әуелі бір түзудің бойымен бағытталған, тербеліс периодтары бірдей ал, амплитудалары мен бастапқы фазаларының айырмашылығы бар екі тербелісті қосудан бастайық. Бірінші тербеліс ал екінші тербеліс заңдылығына бағынатын болсын. Мұндағы 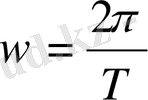тербеліс периодтары бірдей екі гармониялық тербелістің цикілдік жиілігі бір мезетте екі тербеліске қатынасатын дененің тепе-теңдік қалпынан орын ауыстыруы, яғни ығысуы

тең болады. Қорытқы тербелістің амплитудасын тербелістің бейнеленуін пайдаланып, А және бастапқы фазасын анықтайық (5-сурет) .

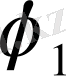
5-сурет. Бір түзудің бойымен бағытталған екі гармониялық тербелісті қосу.

Уақыт t=0 мезеттен есептегенде Х ₁ =A ₁ cosφ, ал Х ₂ =A ₂ cosφ ₂ болады. Модулі бірінші гармониялық тербелістің амплитудасына тең болатын 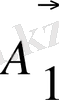векторы О нүктесінен сағат тілінің айналу бағытына қарама-қарсы бағытта бір қалыпты айналысын оның горизантал өспен жасайтын бастапқы бұрышы - φ ₁ болсын. Модулі екінші гармониялық тербелістің амплитудасына тең болатын векторы да О нүктесінен сол бағытта бірқалыпты айналысын делік. Оның горизантал өспен жасайтын бастапқы бұрышы φ ₂ болсын. Қорытқы тербеліс амплитудасын табу үшін және векторларын қосып, векторын анықтауымыз керек. Косинустар теориясын пайдалансақ, онда тербеліс осыдан қорытқы тербелістің амплитудасын анықтаймыз, яғни 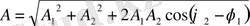тең болады.

Қорытқы тербелістің бастапқы фазасын табу үшін мына қатынасты пайдаланамыз.

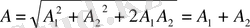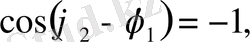Егер бастапқы фазалар айырмасы φ ₂ - φ ₁ = 0 тең болса, яғни онда Сондықтан яғни қорытқы тербеліс амплитудасы жеке тербелістердің амплидудаларының қосындысына тең болады. Сол сияқты фазалар айырмасы тең болса, яғни онда онда 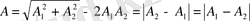қорытқы тербеліс амплитудасы жеке тербелістердің амплитудаларының айырмасына тең болады. Сол сияқты бастапқы фазалар айырмасы 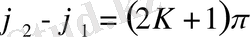тең болса, онда 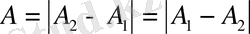болады.

Бастапқы фазалар айырмасы 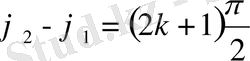болса, сонда 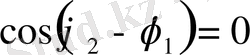Сондықтан 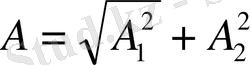тең болады.

Сөйтіп қорытқы тербеліс амплитудасының ең үлкен мәні тең болады да, ең кіші мәні 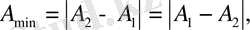яғни

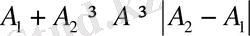
Егер жеке тербелістердің периодтары тең болмас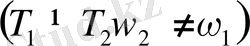а онда және векторлары О нүктесінен әр түрлі цикілдік жылдамдықтармен айналады. Ыңғайлы болу үшін бастапқы фазалар тең болатын жағдайларды қарастыралық. (6-сурет)

6 - сурет. Тармақтары әр түрлі гармониялық тербелістер.

Сөйтіп тең болады. Анық болу үшін деп алайық. Косинустар теоремасы бойынша

тең.

Енді тербеліс амплитудалары А ₁ =А ₂ жағдайды зерттелік. Сонда

Косинустың абсолют мәнінің периоды π-ге тең екені белгілі, сондықтан амплитуданың өзгеру периодын 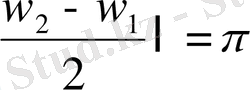өрнегінен табуға болады, яғни 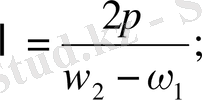Қорытқы тербелістің өзгеру жиілігі тең болады.

Қорытқы тербелістің өзгеру жиілігі жеке тербелістердің жиіліктерінің айырмасына тең. Сөйтіп тербеліс амплитудалары тең, бірдей бағытталған екі гармониялық тербелістің қорытқы тербелісі амплитудасы біресе өсіп, біресі кеміп, отыратын тербеліс болады. Мұндай тербелістерді соғу деп атайды. (7-сурет)

Соғу айқын байқалу үшін тербеліс жиіліктері онша алшақ болмауы керек, яғни соғу кезінде цикілдік жиілік деп алынады.

7-сурет. Соққы тербелісі.

1. 4. Өзара перпендикуляр тербелістерді қосу

Материялық нүкте бір мезетте тербеліс периодтары бірдей бағыттары өзара перпендикуляр екі тербеліске қатысатын болсын. Тербеліс бағыттары ретінде ОХ және ОУ өстерін алайық. Сонда тербеліс теңдеулері былай өрнектеледі. 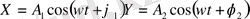Мұндағы А ₁ және А ₂ тербеліс амплитудалары, ал φ ₁ және φ ₂ бастапқы фазалар. Қорытқы тербеліс теңдеуін табу үшін, осы екі теңдеуден уақытты жою қажет әуелі теңдеулерді мынадай қарапайым түрлерге келтірейік: 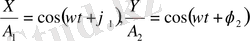қосындысының косинусы туралы теореманы пайдалансақ, мынадай екі өрнекті шығарып аламыз.

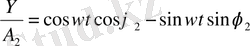
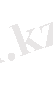
Бірінші өрнектің екі жағын 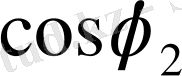-ге, ал екінші өрнектің екі жағын

көбейтіп, олардың айырмасын тапсақ, мынадай өрнек шығады:

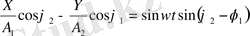Енді бірінші өрнектің екі жағын - ге, ал екінші өрнектің екі жағын көбейтіп, олардың айырмасын тапсақ, мынадай өрнек шығады.

Осы өрнектің екі жағын квадраттап, мүшелеп, қоссақ, қорытқы тербелістің траекториясының теңдеуі шығады.

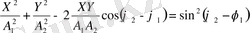
Енді дербес жағдайларды қарастыралық.

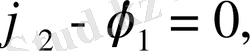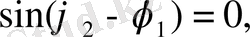
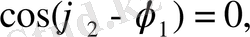1-фазалар айырмасы нөлге тең болсын, яғни сонда болады да, өрнегі шығады. Бұны былай 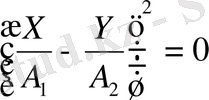жазуға болады. Яғни 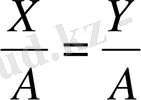немесе бұл теңдеу координаттар басынан өтетін I және III ширектерде жатқан түзудің теңдеуі.

8- сурет. Бастапқы фазалары тең өзара перпендикуляр тербелістерді қосу.

2-фазалар айырмасы π-ге тең болсын, яғни сонда 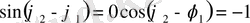болады да, 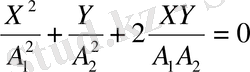өрнегі шығады. Бұны былай 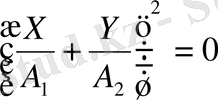жазуға болады, яғни 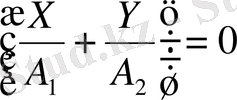немесе 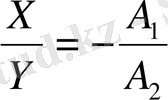Бұл теңдеу координаттар басынан өтетін, II және IV ширектерде жататын түзудің теңдеуі. (9 - сурет)

9- сурет. Бастапқы фазаларының айырмасы π-ге тең тербелістерді қосу.

Егер 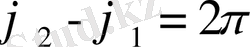- ге тең болса, онда қорытқы тербеліс (8- сурет) суреттегідей болады да, ал 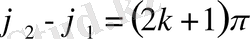- ге тең болса, онда қорытқы тербеліс 9 - суреттегідей болады.

Бастапқы фазалар айырмасы π/2, тақ санына тең болса, яғни /2, онда

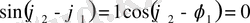
Бұл жағдайда тербеліс траекториясы эллипс болады. (10 - сурет)

10- сурет. Бастапқы фазалар айырмасы π/2 тақ санына тең тербелістерді қосу.

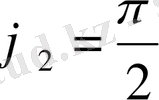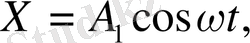
Мысалы , тең болсын делік, онда =π/2. Олай болса 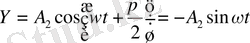Бастапқы уақыт мезетінде (t=0) Х=A ₁ , Y=0 тең болады; яғни материялдық нүкте абцисса өсінде жатыр. Келесі мезетте X>0, ал Y<0 болады, яғни материялық нүкте эллипс бойымен сағат тілінің қозғалу бағытына сәйкес бағытта қозғалады. Егер 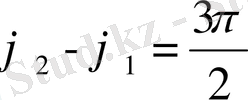болса, материялық нүктенің эйлипс бойымен сағат тілінің қозғалу бағытына қарама-қарсы бағытта болар еді.