Электр тізбектер теориясы: екіполюстіктер, көпполюстіктер мен төртполюстіктердің негізгі теңдеулері, эквивалентті схемалары және мінсіз трансформатор


ЖОСПАР
Кіріспе
1. 1 Екіполюстіктер. Пассивті екіполюстіктер.
1. 2 Көпполюстіктер.
1. 3 Төртұштықтардың негізгі теңдеулері .
1. 4 Төртұштықтардың эквивалентті схемалары.
1. 5 Мінсіз (идеальный) трансформатор.
Қорытынды
Пайдаланған әдебиеттер
Кіріспе
Ғылыми анықтама бойынша Электр Тізбектер Теориясы - электрлік материяның жалпы қасиеттерін, қозғалыстарын зерттейтін іргелі ілім. Сондықтан да ЭТТ-ның дамуы басқа ілімдердің өркендеуіне күшті әсер етеді.
ЭТТ - техниканың іргетасын қалаушы ілімдердің бірі. ЭТТ-да ашылған әрбір заңдылық техниканың дәрежесін жаңа сатыға көтереді, өркендеп-өсуіне әсерін тигізеді. Бұған мысал, XIX ғасырда электромагниттік теорияның дүниеге келуі, ХХ ғасырда жартылай ток өткізгіштердің, кванттық лазерлердің ғылыми лабораторияларынан шығып өмірге келуі.
Электрлік тізбектердің 2 түрі белгілі: сызықты және қисық сызықты . Егер, тізбектің кедергісі тек қана токқа тәуелді болса, сызықты тізбек деп аталады.
Күрделі өткізгіштерде электрлік көздер және энергия қабылдағыштар, өлшеуіш құралдар, көмекші элементтер болады. Көмекші элементтерге қосып- ажыратқыштар жатады. Кез- келген күрделі өткізгіштердің есебін алу үшін, алдымен оның әрбір элементін схемалық элементке алмастырамыз. Тұрақты токта 2 негізгі схемалық элемент қолданылады: электр қозғаушы күш және ішкі кедергі.
Электр қозғаушы күш сан жағынан потенциалдар айырмасына немесе кернеу, яғни оң және теріс, кіріс пен шығыс көздерінің энергиясына тең:
Е= ƒ1- ƒ2 = U 1 , 2
Күрделі электр тізбектерінің жұмыс режимін зерттеу көбінесе ток, кернеу және оның әр түрлі тармақтарының қуаттарының арасында байланыс орнығатынын көрсетеді. Сондай- ақ қалған тізбек бөліктерінің жұмыс режимі белгісіз болып қалуы мүмкін, алайда оның барлық параметрлері есепті шешу кезінде қамтылады.
1. 1 Екіполюстіктер. Пассивті екіполюстіктер.
Кез- келген екіполюстікте ток және кернеу Ом заңымен байланысты болып келеді ( 1- сурет ) .

1- сурет.
U=ZI және I=YU
мұнда, Z жәнеY комплексті кіріс кедергісі мен екіполюстіктің жүргізілуі.
Комплексті кіріс кедергісіне Z= r+jx тізбектей жалғанған активті кедергі r мен реактивті кедергіден x тұратын екіполюстіктің эквивалентті схемасы сәйкес келеді. Сондықтан эквивалентті схемада(1-сурет) -x кедергі шартты түрде тіктөртбұрыш түрінде көрсетілген. U кернеуді құраушыларға жіктесек:
U=ZI=(r+jx) I=rI+jxI=Uа+Uр
Мұнда, Uа= rI- токпен сәйкес келетін фаза құраушы- активті кернеу құраушысы деп аталады.
Uр= jxI- П/2 бұрышына токпен қозғалған сәйкес фаза құраушы- реактивті кернеу құраушысы деп аталады.
Uа мен Uр құраушыларын r және x элементтерінде эквивалентті схемасының кернеулері ретінде қарастыруға болады.
1. 2 Көпполюстіктер.
Көпполюстіктер дегеніміз- ток және оның потенциалдарының арасында байланыс теңдеуін құру үшін қажет және айқындалған параметрлермен берілетін тізбек бөлігі. Көпполюстіктердегі полюс сандары берілген тізбек бөлігінің шектеріндегі қысқыштар санына тең болады. Олар көп жағдайда шартты түрде тіктөртбұрыш белгісімен белгіленеді. 2- суретте пассивті екіполюстік , 3- суретте- үшполюстік , 4- суретте- төртполюстіктің шартты түрде белгіленуін көруімізге болады.

2-сурет. 3- сурет. 4- сурет.
Электр тізбектерін зерттеу барысында электр энергия көздері және қабылдағыштар үшін тіркелген қысқыштары бар екіполюстіктер, үшполюстіктер және төртполюстіктерді қолдануға тура келеді.
Екі жұп қысқыштары бар электр тізбегінің бөлігі т өртполюстіктер деп аталады ( 5- сурет ) . Кіріс (1΄-1˝) деп аталатын жұбына- электрлік көздер, ал шығыс (2΄-2˝) деп аталатын екінші жұбына тұтынушы жалғанады.

5- сурет. Төртполюстіктер.
Тармақ құрамында энергия көздері болмайтын төртполюстіктер- пассивті төртполюстік деп аталады. Оларға мысал ретінде электр энергиясының берілу түзуін және трансформаторларды жатқызуға болады. Керісінше, тармақ құрамында энергия көзі бар төртполюстіктер- активті деп аталады.

6- сурет.
Пассивті төртполюстіктердің режим әдістері мен теориясын зерттеу үшін 2 ЭҚК бар 2 бұтақты бөліп аламыз (6- сурет) . Сонда қалған схема энергия көзі бар схеманы қарастырамыз. Е1 және Е2 электр қозғаушы күштері бөлігін- бірлік кіріс зажимді 1΄-1˝ және екілік кіріс зажимді 2΄-2˝ төртполюстік ретінде қарастыруға болады. Сондай- ақ, энергия көзінің ішкі кедергілері ішкі төртполюстікке қатысты болады. Токтың оң бағыттары және кернеу сәйкесінше ЭҚК бағытымен бағыттас (6- сурет) . Контурлы токтар әдісін пайдаланып (ток I 1 , I 2 және кернеу U 1 , U 2 оң бағытталған ), келесі теңдеуді жазамыз:
E 1 = U 1 = Z 11 I 1 + Z 12 I 2
E 2 = U 2 = Z 21 I 1 + Z 22 I 2
Мұнда I 2 = 0 болғанда Z 11 =U 1 /I 1 , Z 21 = U 2 /I 1 ; (1)
I 1 =0 болғанда `Z 22 = U 2 /I 2 , Z 12 = U 1 /I 2
- теңдеудің жазылу формасы-Z формасыдеп аталады. Оны матрицалық түрде жазса да болады:
U 1 =Z 11 Z 12 I 1 (1А)
U 2 =Z 21 Z 22 I 2
Бұл теңдеуді сондай- ақ түйінді потенциалдар әдісімен де алуға болады. Мұндай жазылу теңдеуінің формасы Y форма деп аталады, оны матрицалық түрде жазуға болады:
│I 1 │ │Y 11 -Y 12 ││U 1 │
=
│I 2 │ │-Y 21 Y 22 ││U 2 │
Транзисторлы төртполюстіктердің анализін алуда аралас(гибридті) параметрлері бар теңдеулер жиі қолданылады. Аралас(гибридті) параметрлі теңдеулерде тәуелсіз айнымалылар болып ток I 1 және кернеу U 2 , ал тәуелд і болып кернеу U 1 және ток I 2 табылады. Бұл теңдеуді (1) - теңдеуден оңай алуға болады:
U 1 = H 11 + H 12 U 2 (2)
I 2 = H 21 + H 22 U 2
H 11 = Z 11 Z 22 - Z 11 - Z 21 / Z 22
H 21 =-Z 21 /Z 22
H 21 = 1/Z 22
Аналогті түрде (1) , (1а) және (2) теңдеулерін Н форма деп атап, оны матрицалық түрде былай жазуға болады:
│U 1 │ │H 11 H 12 ││I 1 │
= (3)
│I 2 │ │H 21 H 22 ││U 2 │
Төртполюстіктерді симметриялық және симметриялық емес деп екіге бөлуге болады. Егер, қабылдағыш және заряд көзі орнын ауыстыру барысында энергия көзі және қабылдағыш токі өэгеріссіз қалса, онда ол симметриялы төртполюстік деп аталады. Бұл шарттарды қанағаттандырмайтын төртполюстіктер симметриялы емес деп аталады.
Төртполюстіктердің тұрақты шамалары болып А, В, С, D шамалары табылады. Олар мына теңдеу арқылы бір- бірімен тығыз байланысты:
AD-BC=1 (4)
U 1 =AU 2 +BI 2 (5)
I 1 =CU 2 +DI 2
Мұнда A=Y 22 /Y 21 - шексіз шама
B=1/Y 21 - кедергі шамасы
C=(Y 11 Y 22 -Y 12 Y 21 ) Y 21 - өткізгіш шамасы
D=Y 11 /Y 21 - шексіз шама.
Бұл теңдеудің жазылу формасы А форма деп аталады .
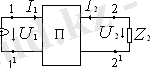
Кез- келген бірлік және екілік қысқыштармен берілген пассивті төртполюстіктер өзара тәуелсіз 3 тұрақты коэффициентпен сипатталатыны жоғарыда айтылған. Демек, пассивті төртполюстікті 3 элеменнті эквивалентті П тәріздес схема түрінде елестетуге болады.

7- сурет.
Егер қорытылып шығарылған мына
I 1 =Y 11 U 1 -Y 12 U 2
I 2 =-Y 21 U 1 +Y 22 U 2
теңдеудің I 1 - ді анықтаушы оң жағына Y 12 U 1 -ді қосып, I 2 - ні анықтаушы 2- теңдеудің оң жағына Y 21 U 2 - ні қосып есептесек, түрлендіре отырып мынандай теңдеу аламыз:
I 1 = (Y 11 -Y 12 ) U1+Y 12 (U 1 -U 2 ) =I 11 +I 12
I 2 =-Y 21 (U 1 -U 2 ) + (Y 22 -Y 21 ) U2=I 22 -Y 21
Алынған теңдеуді 7- суреттегі схема қанағаттандырады. Схеманың элементтері:
Z 3 =1/I 12 ; Z 1 =1/Y 11 -Y 12 ; Z 2 =1/Y 22 -Y 12
U 1 =AU 2 +BI 2
I 1 =CU 2 +DI 2
және
AD-BC=1 теңдеулерін пайдалана отырып, схема параметрлерін төртполюстіктер коэффициенттері арқылы бейнелеуге болады:
Z 3 =B; Z 1 =B/D-1; Z 2 =B/A-1.
Т тәріздес схема элементтерін үшбұрышты эквивалентті жұлдызшаға түрлендіру формуласы бойынша табуға болады (8- сурет ) :
Z 1 ´=Z 3 Z 1 /Z 3 +Z 1 +Z 2 ; Z 2 ´=Z 3 Z 2 /Z 3 +Z 1 +Z 2 ; Z 3 ´=Z 1 Z 2 /Z 3 +Z 1 +Z 2 .
Z 3 , Z 1 , Z 2 теңдеулерінде орнына қою арқылы сәйкесінше келесі теңдеуді аламыз:
Z 1 ´=A-1´/C; Z 2 ´=D-1/C; Z 3 ´=1/C.
Бұл жерде айта кететіні- токтың оң бағытының өзгеруі эквивалентті схема параметрлеріне әсері тимейді.

8- сурет.
1. 3 Төртұштықтардың негізгі теңдеулері .
Пассивті төртұштықтардың жұмыс режимдерін зерттеп, есептеу әдістерін және теорияларын оқып білу үшін, екі энергия көздерінен тұратын схеманы қарастырамыз (1. 1сурет) . Екі
 және
және
 ЭҚК-тері бар тармақтарды бөліп аламыз. Сонда басқа қалған схема бөліктерін пассивті төртұштық деп қарастырамыз.
ЭҚК-тері бар тармақтарды бөліп аламыз. Сонда басқа қалған схема бөліктерін пассивті төртұштық деп қарастырамыз.
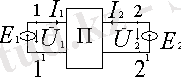
Біріншіден кірер қысқыштары 1-
 және екіншіден шығар 2-
және екіншіден шығар 2-
 қысқыштары бар. Бұл кезде қорек көздерінің ішкі кедергілері төртұштықтың ішіне енгізілген. Кернеулердің және тоқтардың оң бағыттары 1. 1суретіндегідей етіп қабылданып аланған. Контурлық тоқтар әдісін пайдаланып келесі теңдеулерді жазамыз:
қысқыштары бар. Бұл кезде қорек көздерінің ішкі кедергілері төртұштықтың ішіне енгізілген. Кернеулердің және тоқтардың оң бағыттары 1. 1суретіндегідей етіп қабылданып аланған. Контурлық тоқтар әдісін пайдаланып келесі теңдеулерді жазамыз:
 =
=
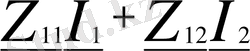

 -параметрі кедергі түріндегі төртұштықтың беріліс теңдеулері. Төртұштықтың беріліс теңдеулерінің коэффициенттері төртұштықтың параметрлері деп аталады.
-параметрі кедергі түріндегі төртұштықтың беріліс теңдеулері. Төртұштықтың беріліс теңдеулерінің коэффициенттері төртұштықтың параметрлері деп аталады.
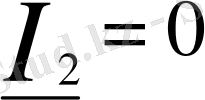 кезінде (бос жүріс режимі, яғни төртұштықтың қорек көзі біріншілік қысқыштары жағынан берілгенде екіншілік қысқыштары ажыратылған) мұндағы
кезінде (бос жүріс режимі, яғни төртұштықтың қорек көзі біріншілік қысқыштары жағынан берілгенде екіншілік қысқыштары ажыратылған) мұндағы
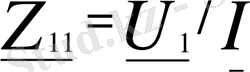 және
және

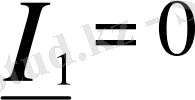 кезінде (бос жүріс режимі, яғни қорек көзі екіншілік қысқыштары жағынан берілген, ал біріншілік қысқыштары ажыратылған)
кезінде (бос жүріс режимі, яғни қорек көзі екіншілік қысқыштары жағынан берілген, ал біріншілік қысқыштары ажыратылған)

 теңдеулерінің жазылу түрін
теңдеулерінің жазылу түрін
 пішінді дейміз, бұл формулалар матрицалық түрде де жазылуы мүмкін.
пішінді дейміз, бұл формулалар матрицалық түрде де жазылуы мүмкін.
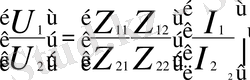 немесе
немесе
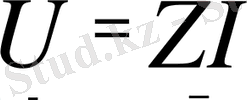 . Егер теңдеуден
. Егер теңдеуден
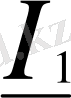 және
және
 тоқтарын
тоқтарын
 және
және
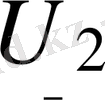 кернеулері арқылы көрсететін болсақ, келесі теңдеуді аламыз:
кернеулері арқылы көрсететін болсақ, келесі теңдеуді аламыз:


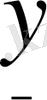 параметірі өткізгіштік түріндегі төртұштықтың беріліс теңдеулері. Мұндағы :
параметірі өткізгіштік түріндегі төртұштықтың беріліс теңдеулері. Мұндағы :
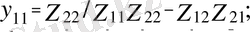
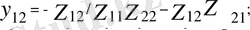

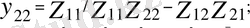
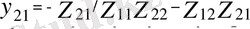 осы теңдеуді тікелей 1. 1 суреттегі схемадан түйіндік потенциялдар әдісін пайдаланып алуға болады. Сонда кірердегі және өзаралық өткізгіштерді келесі қатынастар бойынша анықтайды.
осы теңдеуді тікелей 1. 1 суреттегі схемадан түйіндік потенциялдар әдісін пайдаланып алуға болады. Сонда кірердегі және өзаралық өткізгіштерді келесі қатынастар бойынша анықтайды.
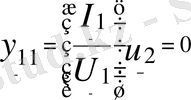 - шығар қысқыштары қысқа тұйықталған кезіндегі кірмелік өткізгіштік.
- шығар қысқыштары қысқа тұйықталған кезіндегі кірмелік өткізгіштік.
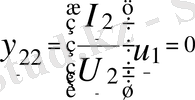 - кірер қысқыштары қысқа тұйықталған кезіндегі, шығар қысқыштары жағындағы кірмелік өткізгіштік.
- кірер қысқыштары қысқа тұйықталған кезіндегі, шығар қысқыштары жағындағы кірмелік өткізгіштік.

 кірер қысқыштары қысқа тұйықталған кезіндегі, аралық өткізгіштік.
кірер қысқыштары қысқа тұйықталған кезіндегі, аралық өткізгіштік.
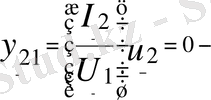 шығар қысқыштары қысқа тұйықталған кезіндегі өзаралық өткізгіштік. Теңдеудің жазылу түрін
шығар қысқыштары қысқа тұйықталған кезіндегі өзаралық өткізгіштік. Теңдеудің жазылу түрін
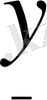 пішінді дейміз, бұл теңдеулерді матрицалық түрде жазамыз:
пішінді дейміз, бұл теңдеулерді матрицалық түрде жазамыз:
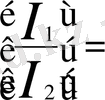

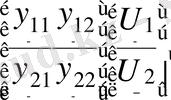 Транзисторлы төртұштыққа талдау жасау үшін аралас(гибрит) параметрлі деп аталатын теңдеулер жиі қолданылады ондағы тәуелді айнымалы ретінде
Транзисторлы төртұштыққа талдау жасау үшін аралас(гибрит) параметрлі деп аталатын теңдеулер жиі қолданылады ондағы тәуелді айнымалы ретінде
 кернеуі және
кернеуі және
 тоғы алынған, ал тәуелдісі
тоғы алынған, ал тәуелдісі
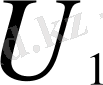 кернеуі және
кернеуі және
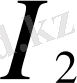 тоғы. Бұл теңдеулер келесі түрде жазыла алады.
тоғы. Бұл теңдеулер келесі түрде жазыла алады.
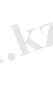
Мұндағы
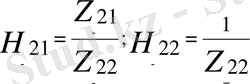 Төртұштықтардың тізбектеліп (каскадтты) жалғанған кездерінде режимдерге зерттеулер жүргізу үшін құрылатын теңдеулердің түрлері
Төртұштықтардың тізбектеліп (каскадтты) жалғанған кездерінде режимдерге зерттеулер жүргізу үшін құрылатын теңдеулердің түрлері
 кетнеуі мен
кетнеуі мен
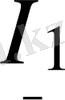 тоқ, және
тоқ, және
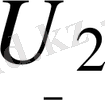 кернеуі,
кернеуі,
 тоғы арқылы көрсетілуі орынды. Осы мақсатта қарымталау(конпенсациялау) жайындағы теория бойынша
тоғы арқылы көрсетілуі орынды. Осы мақсатта қарымталау(конпенсациялау) жайындағы теория бойынша
 ЭҚК-ін,
ЭҚК-ін,
 кедергісіндегі
кедергісіндегі
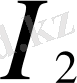 тоқтан пайда болған және қарсы бағытталған кернеу кернеу түсуімен ауыстырамыз.
тоқтан пайда болған және қарсы бағытталған кернеу кернеу түсуімен ауыстырамыз.
Егер төртұштық схемасындағы ЭҚК-і көзін және қабылдағыштағы кедергінің орнын ауыстыратын болсақ, яғни 1-1'қысқыштарына
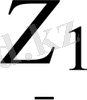 кедергісін, ал 2-2'екі қысқыштарына ЭҚК-і көзін
кедергісін, ал 2-2'екі қысқыштарына ЭҚК-і көзін
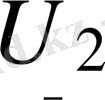 кернеуіне тең етіп жалғасақ және ондағы
кернеуіне тең етіп жалғасақ және ондағы
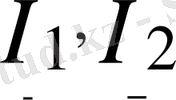 тоқтарының оң бағыттарын керісінше бағытасақ, онда теңдеу келесі түрге енеді:
тоқтарының оң бағыттарын керісінше бағытасақ, онда теңдеу келесі түрге енеді:

1. 4 Төртұштықтардың эквивалентті схемалары.
Барлық пассивті төртұштылар шоғырланған параметрлері бар және кейбір активті төртұштықтылар түрлері өзаралық немесе қайтымды төртұштықтылар деп аталады. Өзаралық төртұштықтылардың параметрлері арасында келесі тәуелділіктер сақталады .
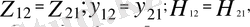 яғни
яғни
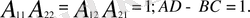
Төртұштытықтылар үштен көп емес тәуелсіз параметрлерімен сипатталады.
Симметриялы төртұштылықтар тек екі тәуелсіз параметрлермен сипатталады, осыдан төртұштылықтылар анықтама бойынша өзара байланысты.
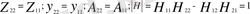
Демек, пассивті төртұштықтарды эквивалентті П-тәрізді схема ретінде және эквивалентті Т-тәрізді схема ретінде көрсетуге болады. П-пішінді схеманың параметрлерін анықтайық.
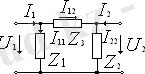
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz