Үшбұрыштардың теңдік белгілері (екі қабырға мен олардың арасындағы бұрыш, бір қабырға мен оған іргелес бұрыштар, үш қабырға) және биіктік, биссектриса, медиана

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ БЕЛГІЛЕРІ

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ БІРІНШІ БЕЛГІСІ

Теорема 3. 1 (екі қабырғасы және олардың арасындағы бұрышы бойынша үшбұрыштардың теңдік белгісі) . Егер бір үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы сәйкесінше екінші үшбұрыштың екіқабырғасы мен олардың арасындағы бұрышына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелдеу. Айталық, ABC және А ₁ , В ₁ , С ₁ үшбұрыштарында <A= А ₁ , АВ = АВ ₁ , АС = А ₁ С болсын (44-сурет) . Үшбұрыштар тең болатынын дәлелдейміз.

Айталық, А ₁ , В ₂ , С ₂ - ABC үшбұрышына тең үшбұрыш болсын, оның В ₁ төбесі А ₁ , В ₁ сәулесінде жатсын, С ₂ төбесі С ₁ төбесімен бір жарты жазықтықта жатсын (45, а-сурет) .

А ₁ В ₁ =А ₁ В ₂ болатындықтан, В ₂ төбесі В ₂ төбесімен беттеседі (45, а-сурет) . <В ₁ , A ₁ С ₁ = <В ₁ , A ₁ С ₁ болғандықтан, А ₁ С ₂ сәулесі A ₁ С ₁ сәулесімен беттеседі (45, в-сурет) . A ₁ С ₁ = A ₁ С ₂ болғандықтан, С ₂ төбесі С ₁ төбесімен беттеседі (45, г-сурет) .

45-сурет

Сонымен, <В ₁ , A ₁ С ₁ үшбұрышы А ₁ В ₂ С ₂ үшбұрышымен беттеседі, демек ABC үшбұрышына тең болады. Теорема дәлелденді.

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ ЕКІНШІ БЕЛГІСІ

Теорема 3. 2 (бір қабырғасы және оған іргелес бұрыштары бойынша үшбұрыштардың теңдік белгісі) . Егер бір үш-бұрыштың бір қабырғасы мен оған іргелес бұрыштары сәйкесінше екінші үшбұрыштың бір қабырғасы мен оған іргелес бұрыштарына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелдеу. Айталық, ABC және В ₁ , A ₁ С ₁ -екі үшбұрыш, оларда АВ = AВ = А ₁ және <A=<A ₁ және <В=<В ₁ болсын (47-сурет) . Үшбұрыштардың тең екенін дәлелдейік.

Айталық, A ₁ В ₂ С ₂ - ABC үшбұрышына тең үшбұрыш болсын, төбесі-А ₁ В ₁ сәулесінде жатсын, ал С ₂ төбесі С ₁ төбесімен түзуіне қарағанда бір жарты жазықтықта жатсын.

\В ₂ = А\В\ болғандықтан, В ₂ төбесі В\ төбесімен беттеседі. А\Сч= /LB\AiC\ және /-А\В\С ₂ = /-А\В\С\ болғандықтан,

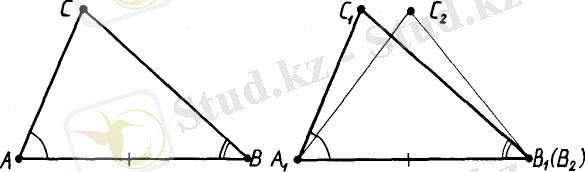
47-сурет

А ₁ С ₂ сәулесі А ₁ С ₁ сәулесімен беттеседі, ал В ₁ С ₂ сэулесі В ₁ С ₁ сәулесімен беттеседі. Б9дан С ₁ төбесі С ₂ төбесімен беттесетіндігі шығады.

Сонымен, А ₁ В ₁ С ₁ үшбүрышы А ₁ В ₂ С ₂ үшбұрышымен беттеседі, демек, ABC үшбұрышына тең болады. Теорема дәлелденді.

ҮШБҰРЫШТЫҢ БИІКТІГІ, БИССЕКТРИСАСЫ ЖӘНЕ МЕДИАНАСЫ

Үшбұрыштың берілген төбесінен түсірілген биіктігі деп осы төбеден үшбұрыштың қарсы жатқан қабырғасын қамтитын түзуге жүргізілген перпендикулярды айтады.

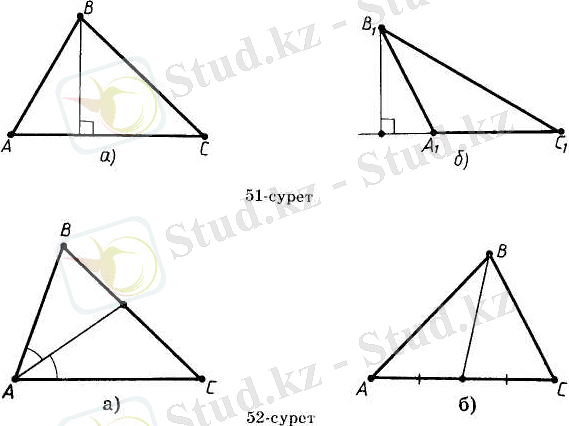
олардың В және В ₁ төбелерінен биіктіктер жүргізілген. 51, а-суретте биіктіктің табаны үшбұрыштың қабырғасында жатыр, ал 51, б-суретте үшбұрыш қабырғасының созындысында жатыр.

Үшбұрыштың берілген төбесінен жүргізілген биссектрисасы деп үшбұрыш бұрышының биссектрисасының осы төбені қарсы жатқан қабырғадағы нүктемен қосатын кесіндісін айтады (52, а-сурет) .

Үшбұрыштың берілген төбесінен жүргізілген медианасы деп осы төбені қарсы жатқан қабырғаның ортасымен қосатын кесіндіні айтады (52, б-сурет) .

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ ҮШІНШІ БЕЛГІСІ

Теорема 3. 6 (үшбұрыштардың үш қабырғасы бойынша теңдік белгісі) . Егер бір үшбұрыштың үш қабырғасы сәйкесінше екінші үшбұрыштың үш қабырғасына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелдеу. Айталық, ABC және А ₁ В ₁ С ₁ үшбұрыштарында АВ = А ₁ В ₁ , AC = A ₁ С ₁ , ВС = В ₁ С ₁ болсын (55-сурет) . Үшбұрыштар тең екенін дәлелдеу керек.

Үшбұрыштар тең емес деп жориық. Сонда <A Equation. 3 < А ₁ , <В Equation. 3 <В _1, <C Equation. 3 C ₁ , болсын. Әйтпесе, олар бірінші белгі бойынша тең болар еді.

Айталық, А ₁ В ₁ С ₁ -ABC үшбұрышына теқ үшбұрыш болсын: оның С ₂ төбесі С ₁ төбесімен А ₁ В ₁ түзуіне қатысты бір жарты жазықтықта жатсын (55-суретті қараңдар) .

D нүктесі - С ₁ С ₂ кесіндісінің ортасы болсын. Сонда А ₁ С ₁ С ₂ және В ₁ С ₁ С ₂ - үшбұрыштары тең бүйірлі, ал С ₁ С ₂ бұларға ортақ табан болады. Сондықтан бұлардың A ₁ D және B ₁ D медианалары биіктіктер де болып табылады. Демек, A ₁ D және B ₁ D түзулері С ₁ С ₂ түзуіне перпендикуляр болады. A ₁ D және B ₁ D түзулері беттеспейді, өйткені А ₁ , В ₁ . D нүктелері бір түзуде жатпайды. Ал С ₁ С ₂ түзуінің D нүктесі арңылы оған тек қана бір перпендикуляр түзу жүргізуге болады. Біз қайшылыққа келдік. Теорема дәлелденді.