Толық дифференциалды теңдеулер: толықтық шарттары, шешім табу әдістері және интегралдаушы көбейткіштері


Толық дифференциалды теңдеу
Тағы да квадратураға келтірілетін теңдеулердің бір класын қарастырайық.
Айталық, бірінші ретті дифференциалдық теңдеу х , у бойынша симметриялық дифференциалдық түрінде берілсін:
М(х, y) dx + N. (x, y) dy = 0 (1)
Кейбір жағдайларда, сол жағындағы өрнек бір функцияның толық дифференциалы болуы мүмкін, яғни,
dU(x, y) = M(x, y) dx + N(x, y) dy. Егер ондай шарт орындалса, онда (1) теңдеуі толық дифференциалды теңдеу деп аталады жане былай жазылады:
dU (x, y) = 0 (2)
Онда теңдеудің шешімін мына түрде табуға болады:
U(x; у) - С, С - тұрақты сан.
Осыдан, толық дифференциалды (2) теңдеудің шешімін табу үшін, оның сол жағындығы өрнегін толық дифференциал жасайтын U(x, у) функциясын табу керек екен.
Мысалы cos(x - y) dx - cos(y - x) dx = 0 теңдеуі берілсін. Бұл теңдеудің сол жағы и = sin(x - у) функциясының толық дифференциалы болады, сондықтан, sin( х - у) - С - берілген теңдеудің жалпы интегралы болады. Бұл мысалда U(х, у) функциясы оңай табылды (теңдеу қарапайым болғандықтан) . Көп жағдайда оны табу қиынға соғады, тіпті ол болмауы да мүмкін. Сондықтан, жалпы жағдайда, сондай функцияларды табу әдістерін қарастырайық.
Айталық жабық, шенеуді бір байланысты D облысында
M(x, y), N(x, y)
және
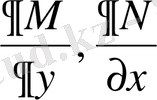 үзіліссіз функциялар болсын.
үзіліссіз функциялар болсын.
Сонда
Mdx \ Ndy
өрнегі
D
облысында
U(x, y)
функциясының толық диффереяциалы болу шарты
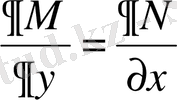 теңдігіне әкелетінін білеміз.
теңдігіне әкелетінін білеміз.
Егер осы теңдік орындалса, онда U(x, y) функциясына
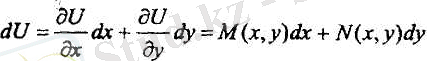
теңдігі орындалады.
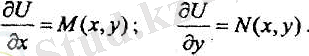 Осыдан
Осыдан
(4)
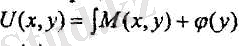 Бірінші тендікті ингегралдасақ
Бірінші тендікті ингегралдасақ
(5)
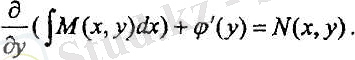 болады. Бұл жерде φ
(у) - у
-тен тәуелді белгісіз функция. Осы функцияны (4) -тің екінші теңдеуі орындалатындай етіп, таңдау керек. Ол үшін (125. 5) -тің оң жағын
у
бойынша туыңдысын тауып
болады. Бұл жерде φ
(у) - у
-тен тәуелді белгісіз функция. Осы функцияны (4) -тің екінші теңдеуі орындалатындай етіп, таңдау керек. Ол үшін (125. 5) -тің оң жағын
у
бойынша туыңдысын тауып
N(x, у) -ке теңестіреміз:
Осы теңдеуде φ (у) -ті тауып (5) формуласына қоямыз, сонда (5) теңдеудің U(x, у) = С - жалпы шешімін табамыз.
Толық дифференциалды теңдеудің шешімін табатын тағы да бір формулаларын дәлелдеусіз келтірейік:
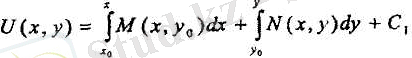
және
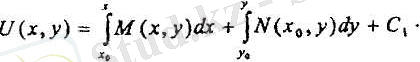
Енді С 1 = 0 деп алып, (5-формуланы пайдаланатын болсақ, онда (5) жалпы интегралдарын мына түрде жазуға болады:
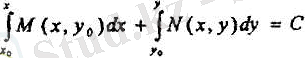
және
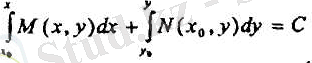
Бұл жерде х 0 және у 0 кез келген сандар, бірақ ( х 0 , у 0 ) және (х, у) нүктелерін қосатын сызық D облысында жату керек.
1-мысал. (3 х 2 + 6 ху 2 ) dx + (6х 2 у + 4у 3 ) dy - 0 теңдеудің шешімін табу керек.
Шешуі. Бұл теңдеуде М(х, у) -3х 2 +6ху 2 ,
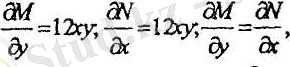 N(x, y) = 6x
2
y + 4y
3
.
N(x, y) = 6x
2
y + 4y
3
.
Туындыларын табамыз:
яғни берілген теңдеу - толық дифференциалды. Онда (5) пайдалансақ:
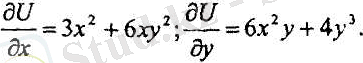
болады. Бұл жерде U(x, y) - ізделетін функция. Оны табу үшін бірінші теңдеуден
U(x, y) =
 (
3
х
2
+ 6xy
2
) dx + φ(у) = х
3
+ 3х
2
у
2
+ φ(у)
(
3
х
2
+ 6xy
2
) dx + φ(у) = х
3
+ 3х
2
у
2
+ φ(у)
болады. Енді φ (у) -ті табу үшін (5) -дін екінші теңдеуін пайдаланамыз:
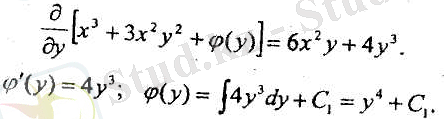
Сонда осы тапқан φ (y) -ті (5) -ға қоятын болсақ:
U(x, y) = x 3 +3х 2 у 2 + у 2 +С 1 .
Бұдан dU(x, y) = 0 болады, сондықтан U(х, у) = С 2 немесе х 3 + 3х 2 у 2 + у 4 + C 1 =C 2 болады.
Сонымен, осы мысалда берілген теңдеудің жалпы шешімі мына түрде жазылады; х +3x 2 y 2 +y 4 =C; (C = C 2 -C 1 ) .
2-мысал. (3х 2 +2ху-у 2 ) dх + (х 2 -2ху-3у2) dу = 0 теңдеуді шешу керек.
Шешуі. Бұл теңдеуде
М(х, у) = 3х
2
+2ху - у
2
; N(x, y) = х
2
-2ху-3у
2
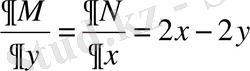 үзіліссіз функциялар, яғни теңдеу толық дифференциалды. (5) формуланы қолданамыз
(х
0
=0, у
0
=О) :
үзіліссіз функциялар, яғни теңдеу толық дифференциалды. (5) формуланы қолданамыз
(х
0
=0, у
0
=О) :
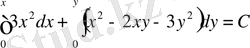
немесе х 3 + х 2 у - ху 2 - у 3 = С - берілген теңдеудің жалпы интегралы болады.
3-мысал.
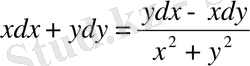 теңдеуі берілген.
теңдеуі берілген.
Шешуі. Теңдеуді мына түрге келтірейік:
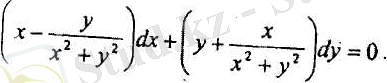
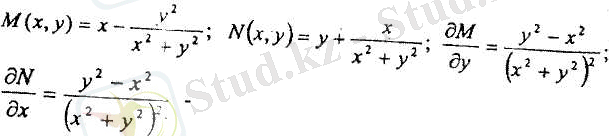 Мұнда
Мұнда
барлығы (0(0, 0) нүктеден басқа) жазықтық нүктелерінде үзіліссіз функциялар. Берілген теңдеу толық дифференциалды. Егер х 0 = 0; у 0 = 1 деп алсақ онда (12. 7. 7) формуладан
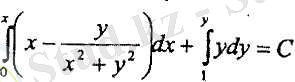
немесе
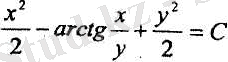
берілген теңдеудің жалпы интегралы болады.
Ескерту.
Егер (12. 7. 1) теңдеудін сол жағы толық дифференциалдық шартын қанағаттандырмаса, яғни
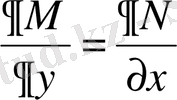 теңігі орындалмаса, онда интегралдаушы көбейткіш деп аталатын λ
(х, у)
функциясын (12. 7. 1) теңдеудің екі жағына көбейтіп, толық дифференциалды болу шарты мына түрде қарастырылады:
теңігі орындалмаса, онда интегралдаушы көбейткіш деп аталатын λ
(х, у)
функциясын (12. 7. 1) теңдеудің екі жағына көбейтіп, толық дифференциалды болу шарты мына түрде қарастырылады:
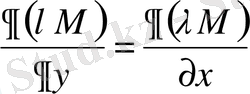
Осы шарт арқылы λ (х, у) - ті тауып, (12. 7. 1) теңдеуді толық дифференциалды түріне келтіреді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz