Сызықты программалау есептері және оларды шешу әдістері

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 34 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . . 5

1 Негізгі бөлім . . . 8

1. 1 Сызықтық программалау . . . 8

1. 2 Сызықтық программалау есептері . . . …… . . . 9

1. 3 Сызықты программалау есептері (СПЕ) модельдерінің түрлері және құру жолдары . . . 12

1. 4 Симплекс әдісі . . . 21

1. 5 Биллдің әдісі . . . 23

1. 6 Баранкина-Дорфман әдістері . . . 25

1. 7 Франк-Вольфа әдістері . . . 27

1. 8 Квадраттық программалаудың екілік әдісі . . . 31

1. 9 Сызықтық программалау есептерін графикалық әдіспен шешу . . . 31

2 Тәжірибелік бөлім . . . 35

Қорытынды . . . 37

Қолданылған әдебиеттер . . . 38

Кіріспе

Қазіргі заманғы қоғамның дамуы мынандай деңгейлермен сипатталады: техникалық деңгейдің жоғарлауы, өндірістің ұйымдастыру құрылымдарын қиындату, еңбек бөлімін тереңдету, жоспарлау әдістерімен шаруашылық басшылықтарына жоғарғы талаптар қою. Бұл жағдайларда басшыларға қоғамның экономикалық өміріне ғылыми тәсілдер қолдану халық шаруашылығының қарқынды дамуына ықпал етеді.

Болашақ бағдарламашылар үшін қолданылған математиканың ең маңызды саласының бірі - математикалық бағдарламалау; Ол экстремальды есептерді зерттеуге және оларды шешу әдістеріне арналған. Бұл пәнді оқу студентке қарапайым экономикалық есептердің математикалық модельдерін құрастыруда алғашқы қадам жасауға, математикалық қойылыммен шешу әдістерін үйренуге мүмкіншілік береді.

Бұл пән жоғарғы математикалық курсынан кейін оқылуы тиіс; бұл жерде сызықтық алгебра мен шектелген өлшемді кеңістіктегі дөңес жиындар теориясының рөлі өте маңызды. Математикалық бағдарламалауды оқу кезінде алған білімін студент мамандығы бойынша экономика-математикалық модельдерін құрастыру, осыдан алнатын математикалық есептерді қою. Оның алгоритімін құрастыру және есептеу техникасын, пайдаланып, шешімдерін табу үшін қолданылады.

Қойылу шарттарына байланысты математикалық бағдарламалау есептері 2 түрге бөлінеді. Сызықтық бағдарламалау негіздері және сызықтық емес бағдарламалау есептері. Олардың ішінде сызықтық бағдарламалау есептері жақсырақ зерттелген. Олар үшін қуатты шешу тәсілдерімен ЭЕМ үшін құрастырылған қолданбалы бағдарламалар пакеттері бар. Осыған байланысты көпшілік жағдайда сызықтық есептер қарастырылып, экономика есептерінің математикалық модельдерін сызықтық бағдартамалау есебіне келтіруге тырысады. Сызықтық емес бағдарламалау есептерін шешу тәсілдері де бар: бірақ олардың өзіне тән қиыншылықтары болғандықтан оған сәйкес модельдер әзірше азырақ қолданылуда.

Математикалық бағдарламалау ғылым саласы және оқу пәні ретінде кейінірек пайда болған; күрделі экономика есептерін шешу қажеттілігі, үйлесімді шешімдер жиынынан ең тиімдісін (оптималь) таңдау және басқалар математикамен есептеу техникасын экономика саласына еңгізуші себепші болады. Бұл математикалық экономиканың немесе математикалық бағдарламалардың пайда болуына әкеледі.

Экономика ғылымының әрі қарай дамуына қажетті шарттарының бірі сандық анализдің нақты әдістерін қолдану және математиканы кеңінен қолдану. Қазіргі уақытта математика мен қазіргі заманға есеп технологиясының жетістіктері экономикалық зерттеулер мен жоспарлауда кең қолданыс табуда. Бұл математика, математикалық программалау сияқты, ойын теориясы, көпшілікке қызмет ету теориясы және де тез әрекеттегі электронды есептеуіш техникасының толқынды дамуы бөлімдерінің дамуына ықпал етеді.

Математикалық әдіс арқылы экономикалық есептерді шешу және орнатуда едәуір нәтиже жинадық. Әсіресе оптимальды жоспарлау әдісі табысты дамуда, бұлар математикалық программалаудың мәні болып табылады. Негізгі болып оптимальді жоспарлаудың бірыңғай жүйесін құру есебі және халық шаруашылығын басқаруды математикалық әдіспен және электронды есептеуіш технологиясын экономикада қолдану.

Экстремалды экономикалық есептерді шешуді мынадай 3 этапқа бөлуге болады:

Экономика-математикалық модельді құру;
Белгілі бір математикалық метод арқылы оптимальді шешімді табу;
Халық шаруашылықтарына экономикалық және өндірістік процестердің нұсқасын енгізу.

Экономика - математикалық модельді құру, біріншіден, зерттелінетін экономикалық процесстің математикалық моделін құруы, ол оның мәнін көрсететін құрылымы. Басқа сөзбен айтқанда, мұндай модельде есептің маңызды өзгешелігі есептелуі керек және де шек қою шарттары, олар нәтижеге ықпал етуі мүмкін.

Математикалық программалаудың құрама бөлімдері сызықты, сызықты емес және динамикалық программалау болып табылады. Бірінші рет сызықтық программалау есебінің орнатылуы совет экономисті А. Н. Толстойдың (1930 ж) жұмысында берілген. 1931 ж. Венгрлік математик Б. Эгерварн математикалық құрылымды қарастырып, сызықты программалаудың есебін шешті, ол «таңдаудың келелі мәселесі» деп атқа ие болды, шешу әдісі венгерлік әдіс деген ат алды. Шешім шығару жолдардың жарату мүмкіндіктері болады, ол алгоритмдердің шешім шығару үшін электрондық есептеуіш машиналарын есептерге қолданады.

1 НЕГІЗГІ БӨЛІМ

1. 1 Сызықтық программалау

Сызықтық программалау - сызықтық функциялардың зерттеу методикасы және экстремалды (аз және көп) мағыналарын іздестіру жайлы ғылым, және сызықтық шектеулері бар.

Сызықтық программалаудың тапсырмасын келесі түрде құруға болады.

Экстремалды мақсат функциясын табу

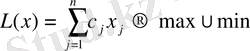(1. 1. 1)

Келесі шектеулерде

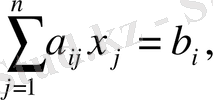i=1, m (1. 1. 2)

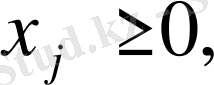j=1, n (1. 1. 3)

Мақсат функциясын (1. 1. 1) сызықтық форма деп те атайды. Бұл жүйені (1. 1. 2) сызықтық программалау тапсырмасының шектеулі теңдеу жүйесі деп атайды.

Жүйенің шешімі (1. 1. 2) немесе баламалық жүйе деп кез- келген n- нің 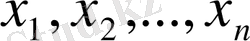бір уақытта барлық теңдеулер жүйесін қанағаттандырады.

Кез-келген теріс шешім жүйесі (1. 1. 2) рұқсат етілген шешім деп аталады.

Базисті шешім деп шешім немесе вектор 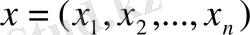теңдеулер жүйесінің (1. 1. 2) барлығы сызықтық тәуелсіз егер болса.

Сызықтық программалаудың тапсырмасы деп айтылмаған, егер оның әр жоспары r дұрыс координатына тең.

Көптеген бар шешімдер сызықтық программалауда дөңес болып келеді, ол сызықтық шектеулердің (1. 1. 2) және (1. 1. 3) ең төменгі жүйесі болып табылады.

1. 2 Сызықтық программалау есептері

Көп есептер оптимизациясы сызықсыз программалауға жатады, бірақ сызықсыз есептерді шығару бұл - өте қиын математикалық шығару проблемасы. Сондықтан да, іс жүзінде барлық шынайы қосымшаларда сызықсыз есептерді шығаруда жақын әдіс ретінде қолданылады. Сызықтық программалау барлық программалау әдістері ішінде көп процедураларды шығарудың негізінде ерекшеленеді.

Сызықтық программалаудың математикалық есептері келесі жолмен қойылады: сызықтық форманың максимумы ізделінеді (мақсат функциясы)

Сызықтық программалаудың жалпы есебі

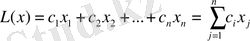
егер

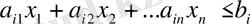
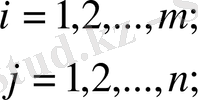
немесе

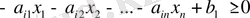
Сөйлем жүзінде сызықтық программалаудың есептерін былай құрастыруға болады: n басталған сызықты форманың максимумын табу керек, ауыспалы m шектеу тепе-теңдік немесе теңсіздігі, өйткені өзгермелі қосымша 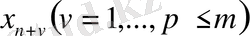теңсіздігін әрқашанда тепе - теңдік етуге болады. Осылай, шектеу

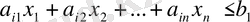(1. 2. 1)

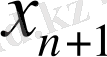қосымшасын қосу арқылы тепе - теңдік етіп өзгерте аламыз

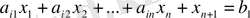
(1. 2. 2)

Сонда (1. 2. 1) жағдайы (1. 2. 2) жағдайымен жинақталады және 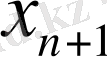қосымшасынның теріс емес екендігіне қарағанда. Сондықтан айтуға болады, сызықтық программалаудың есебін шығарғанда мынандай n қосымшасын 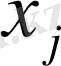сызықтық форманың максимумына айналдыру

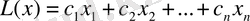
m тепе - теңдігі болады деген шартпен

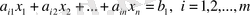
және n тепе - теңсіздігінде ,

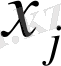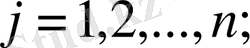
Сызықтық бағдарламалау есептерін шешудің негізгі тәсілі Симплекс тәсілі болып табылады. Ол тәсілдің авторы АҚШ ғалымы Д. Ж. Данциг және оның оқутышылары. Қазіргі кезде ол тәсілдің әр түрлі алгоритмдері мен түрлері (модификациялары) компьютерді пайдалануға арналып құрастырылған. Симплекс тәсілін пайдалану үшін алдымен есеп сызықтық программалаудың негізігі есебі (СБНЕ) түрінде жазылуы тиіс. Ол былайша жазылады.

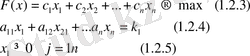
Сонымен теңдеулер жүйесінің (1. 2. 4) қанағаттандыратың теріс емес мәндер қабылдайтың (1. 2. 5) және мақсат функциясының (1. 2. 3) максимумына сәйкес келетің 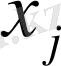белгісіздерінің мәнін табу керек. Егер мақсат функциясының 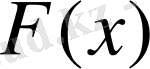минимумы ізделінсе, онда оның таңбасын ауыстыру арқылы максимумында қарастыруға болады.

Егер берілген сызықтық бағдарламалау есебінде теңсіздіктер болса, онда қосымша белгісіздерді енгізу арқылы олар теңдеулерге айналдыруға тиіс.

Мысалы, есепте мынадай теңсіздік болсын делік:

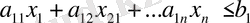(1. 2. 6)

Онда жаңа 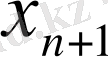айнымалысы енгізіліп, бұл теңсіздік былайша теңдік түрінде жазылады.

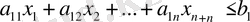(1. 2. 7)

Ескерту: Еңгізілетің жаңа айнымалылар саны теңсіздіктердің санына тең болады. СБНЕ - нің (1. 2. 3) кейбір анықтамаларымен оның шешімдері мен қасиеттері.

Анықтама : Берілген СБНЕ - нің (1. 2. 3) - (1. 2. 5) үлесімді шешімі деп оның шарттарын (1. 2. 4) - (1. 2. 5) қанағаттандыратың кез келген 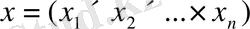векторын атаймыз.

Анықтама : Егер үйлесімі шешім мақсат функциясының F(x) максимумын берсе, ол тиімді шешім деп аталады.

Теорема 1 : СБНЕ - нің үйлсімді шешімдеріні облысы дөңес болады, егер ол бос болмаса.

Теорема 2 : СБНЕ - нің тиімді шешімі үйлесімді шешімдер облысының төбелерінің бірінде болуға тиіс.

Анықтама : Үйлесімді шешімдер облысының төбесіне сәйкес шешімді таяныш шешім деп атайды.

Теорема 3 : Егер тиімді шешім екі немесе одан да көп төбеде болса, онда сол шешімдердің кез келген сызықтық комбинациясында болады.

Теорема 4 : СБНЕ - нің мақсат функциясының максимумы болу үшін келесі шарт орындалуға тиіс.

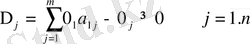(1. 2. 8)

Бұл шарт тиімді шарт деп аталады.

1. 3 Сызықтық программалау есептері (СПЕ) модельдерінің түрлері және құру жолдары

Сызықтық теңсіздіктер және олардың СПЕ орны

Экономикалық, техникалық және басқа жоспарлау есептерін құруда теңсіздіктердің маңызы зор. Алгебралық теңсіздіктердің көмегімен көптеген есептердің шарттарын математика тілінде жазуға болады.

Алгебралық теңсіздіктердің тәжірибелік сызықты программалау есептерінде қолдану негізін түсіну үшін біраз қарапайым мысалдар қарастырайық.

1-есеп. Менеджер тігін фабрикасына екі түрлі матадан екі үлгіден киім тігу жұмысының ұтымды жоспарын құруы керек. Әрбір үлгіде тігілетін киімге матаның екі түрі пайдаланылатын болсын. Әрбір үлгіден бір киім тігуге төменгі кестеде көрсетілгендей әр мата метрі қажет делік.

Бұл көрсеткіштерді экономика ілінде нормативтік коэффициенттер деп атайды.

1. 3. 1- кесте

Тігілетін киім

1- мата, м

2- мата, м

Тігілетін киім:

1 үлгідегі

2 үлгідегі

1- мата, м:

0, 6

0, 8

2- мата, м:

1, 2

0, 6

Тігін орнында матаның бірінші түрінен 24 метр, екінші түрінен 36 метр болсын. Ал бірінші үлгі бойынша тігілген киімнің бағасы 16 мың теңге, екінші үлгімен тігілген киімнің бағасы 12 мың теңге болса, қолдағы бар матадан қандай үлгіден қанша тігілгенде ең көп табыс келтіретін жоспар жасау қажет.

Есепті шешу үшін бірінші үлгіден жасалатын киімнің бізге белгісіз саны Х, ал екінші киімнің санын Х деп алайық. Бұл белгілеу бойынша тігілген киімдерден түсетін жалпы табысты былай өрнектеуге болады:

Z = 16X ₁ + 12X ₂ → max

Мұндағы: 16Х ₁ - бірінші үлгідегі киімнен түсетін табыс. 12Х ₂ екінші үлгілегі киімнен түсетін табыс, ал Z екі үлгідегі киімнен түсетін жалпы табысты көрсетеді. Есептің шарты бойынша Z ең көп табыс болу керек, сондықтан ең көп (ең үлкен) дегенді максимум немесе қысқаша математика тілінде MAX деп белгілеуге болады.

Енді есептің шарттарын жазайық. Бірінші матадан бірінші үлгідегі киімнің бір данасына 0, 6м керек болса, Х данасына 0, 6Х ₁ қажет болар еді, ал осы матадан екінші үлгідегі бір дана киімді жасау үшін 0, 8 м керек болса, Х данасына 0, 8Х ₂ қажет. Екі үлгідегі киімге жұмсалатын матаның қолда бары 24 м - ден артпауы керек. Ендеше бірінші мата үшін мына теңсіздік орындалады:

0, 6Х ₁ + 0, 8Х ₂ ≤ 24

Сол сияқты теңсіздікті екінші мата үшін жазайық:

1, 2Х ₁ + 0, 6Х ₂ ≤ 36

Алгебралық теңсіздіктерді шешкенде Х ₁ мен Х ₂ мәндері теріс сандар да болуы мүмкін. Ал қарастырылып отырған есепте Х ₁ мен Х ₂ - нің мәндері тек оң сан немесе нөл болуға тиіс. Белгісіздердің мәндері оң сан болса, онда белгіленген үлгілі киім тігіледі, ал нөлге тең болса, онда ол киім тігілмейді дегенді білдіреді. Белгісіздің мәні болуы мүмкін емес. Ендеше жоғарғы шарттармен қоса есепке мынадай шарттар қосу қажет:

Х ₁ ≥ 0, Х ₂ ≥ 0

Сонымен есепте қойылған шарттарды математикалық түрде былай өрнектеуге болады:

Z=16X ₁ + 12X ₂ → max

0. 6 X ₁ + 0. 8 X ₂ 24

1. 2 X ₁ + 0. 6 X ₂ 36

X ₁ 0, X ₂ 0

Нәтижесінде берілген СПЕ қарапайым математикалық моделі тұрғызылды.

2-есеп. Менеджер әр түрлі кәсіпорындарға 1 доллар ақшаны инвестиция (кредит) ретінде бөліп орналастырмақшы.

Менеджер жылдық табыстан келісілген пайыз мөлшерінде келетін ақшадан максималды пайда табу үшін, осы кредитті әр кәсіпорнына тиімді орналастыру жоспарын құруы керек.

Кәсіпорындардың аттарын: А, В, С, Д -деп белгілейік. Келісім шарт бойынша әр кәсіпорын жылдық табыстың мынадай пайыздарын қайтаруға міндетті: А- 6%, В- 8%, С- 10% және Д- 9%. Сонымен қатар, әр кәсіпорында қауыпсіздік немесе тәуекелділік (риск) дәрежесі, капиталдың қайтымы, басқа нарық жағдайлары, мысалға салық төлеу саясаты және т. б түрлерңі белгілі болсын.

Инвестиция жұмысының ққауыпсіздігін азайту үшін менеджер капиталдың жартысынан кем емес бөлігін А және В кәсіпорындарына орналастыруға, сонымен қатар капиталдың қайтымдылығын (ликвидность) қамтамасыз ету үшін барлық ақшаның 25 % астам бөлігін Д кәсіпорынына орналастыруға шешім қабылдады. Өкіметтің саясатының өзгеруіне байланысты С кәсіпорнына 20 % аспайтын, ал салық саясатының ерекшелігіне байланысты барлық капиталдың 30 % кем емес бөлігін А кәсіпорнына орналастыру керек.

Шешімі: Әр кәсіпорнына бөлінген оптималды инвестиция мөлшерін: А-Х ₁ мың доллар, В-Х ₂ мың доллар, С-Х ₃ мың доллар және Д-Х ₄ мың доллар деп белгілейік.

Барлық кәсіпорынның жылдық табысынан бөлінген пайыздан түсетін ақша өлшем бірлігіндегі мөлщері максималды болуы қажет, яғни:

Z=0, 06X ₁ +0, 08X ₂ +0, 10X ₃ +0, 09X ₄

Сонымен қатар мынадай шарттар орындалуға тиіс:

• барлық инвестиция мөлшері

Х ₁ +Х ₂ +Х ₃ +Х ₄ < 1;

• инвестиция қауыпсіздігін (риск) қамтамасыз ету

Х ₁ + Х ₂ > 0. 05 (Х ₁ + Х ₂ + Х ₃ +Х ₄ ) ;

• капиталдың қайтымдылығын (ликвидность) қамтамасыз ету

Х ₃ > 0, 25 (Х ₁ + Х ₂ + Х ₃ +Х ₄ ) ;

• өкіметтің саясаты бойынша

Х ₂ > 0, 20 (Х ₁ + Х ₂ + Х ₃ +Х ₄ ) ;

• салық салу саясаты бойынша

Х ₁ > 0, 30 (Х ₁ + Х ₂ + Х ₃ +Х ₄ ) ;

• белгісіздердің теріс болмау шарты

Х ₁ 0; Х ₂ 0; Х ₃ 0; Х ₄ 0

Сызықты программалау есебіне қойылатын талап бойынша әр теңсіздіктерде белгісіздер теңсіздіктің сол жағында, ал тұрақты шамалар оның оң жағында орналастырылады. Олай болса есепті қарапайым түрлендіруден кейін, оның математикалық моделін былай жазуға болады:

• барлық табыстан бөлінетін пайыздың ақшалай өлшемін максималдау

Z=0, 06X ₁ +0, 08X ₂ +0, 10X ₃ +0, 09X ₄

• барлық инвестиция мөлшері

Х ₁ + Х ₂ + Х ₃ +Х ₄ < 1;

• инвестиция қауыпсіздігін (риск) қамтамасыз ету

0, 95Х ₁ +0, 95Х ₂ - 0, 05Х ₃ -0, 05Х ₄ > 0;

• капиталдың қайтымдылығы (ликвидность) қамтамасыз ету

0, 25Х ₁ +0, 75Х ₂ > 0;

• өкіметтің саясаты бойынша

-0, 20Х ₁ -0, 20Х ₂ +0, 80Х ₃ -0, 20Х ₄ > 0;

• салық салу саясаты бойынша

0, 70Х ₁ -0, 30Х ₂ -0, 30Х ₃ -0, 30Х ₄ > 0;

• белгісіздердің теріс болмау шарты

Х ₁ 0; Х ₂ 0; Х ₃ 0; Х ₄ 0

Сонымен СПЕ қарапайым математикалық моделін тұрғыздық.

Бұл есептерден тәжірибелік СП есептері үшін алгебралық теңсіздіктің маңызды екендігін байқаймыз.

3-есеп. Өндіріс орны үш топ станокты пайдаланып, екі түрлі зат шығарады. Тәулігіне 1-топтағы станоктар 400 сағат, ІІ -топтағы станоктар - 360 сағат, ал ІІІ- топтағы станоктар - 3200 сағат жұмыс атқара алады. Бір заттың бір данасын шығаруға жұмсайтын станоктардың уақыты төмендегі кестеде көрсетілген. Негізінде бұл көрсеткіштерді экономикалық тілде техникалық - экономикалық нормативтік коэффиценттер деп атайды.

1. 3. 2- кесте

Станоктар топтары: Станоктар топтары

Бір дана затқа қажетті уақыт мөлшері, сағат: Бір дана затқа қажетті уақыт мөлшері, сағат

Станоктар топтары: І зат - А

Бір дана затқа қажетті уақыт мөлшері, сағат: ІІ зат - В

Станоктар топтары:

1 топ

2 топ

3 топ

Бір дана затқа қажетті уақыт мөлшері, сағат:

0, 4

0, 9

10, 0

2, 0

1, 2

4, 0

Бірінші заттың бір данасынан өндіріс орны 1, 20 мың теңге, екінші заттың бір данасынан 4, 80 мың теңге пайда алатын болса, станоктардың жұмыс жасай алатын берілген уақытын (қорын) тиімді пайдалана отырып, әр заттан қанша жасағанда өндіріс орнының ең көп пайда табатын жоспарын құру керек. Есептің мазмұны ұғымды болу үшін 1-затты - А заты, 2-затты - В заты деп атайық. Ал А - затының максималды пайда беретін санын Хı дана, В - затының максималды пайда беретін санын Х ₂ дана деп белгілейік. Есептің шарты толығымен формалданып бітті. Олай болса, есептің математикалық моделін құруға өтуге болады.

Есептің шарты бойынша бірінші топтағы станок А затының бір данасын жасау үшін 0, 4 сағат уақыт жұмыс істейді, олай болса Х ₁ дананы жасау үшін 0, 4Х ₁ қажет. Ал осы бірінші топтағы станок В затынан бір дана жасау үшін 2 сағат жұмыс істейді, онда Х ₂ дана заты жасау үшін 2Х ₂ сағат уақыт керек. Олай болса 1 - станоктың А және В заттарының Х ₁ және Х ₂ данасын жасау үшін жұмыс уақыты олардың тәулік ресурсынан, яғни 400 сағаттан аспауы керек:

0, 4Х ₁ +2, 0Х ₂ < 400

Осы сияқты теңсіздіктерді ІІ жәнеІІІ топтағы станоктар үшін жазсақ, олар мына теңсіздіктермен өрнектелінеді:

0, 9Х ₁ + 1, 2Х ₂ < 360

10Х ₁ + 4, 0Х ₂ < 3200

Өндіріс орнының алатын пайдасы:

Z= 1, 2X ₁ + 4, 8X ₂

Сонымен біз берілген есептің төменгідей математикалық моделін тұрғыздық:

Z(X ₁ , X ₂ ) = 1, 2X ₁ + 4, 8X ₂ → max,

мына жағдайда:

0, 4Х ₁ + 2, 0Х ₂ < 400

0, 9Х ₁ + 1, 2Х ₂ < 360

10, 0Х _ı +4, 0Х ₂ < 3200

Х ₁ > 0, Х ₂ > 0

Есептің негізгі мақсаты функциямен өрнектелген пайданың ең үлкен мәнін іздеумен түсіндіріледі. Бұл мәнді жай алгебралық жолмен табуға бола ма деген заңды сұраққа жауап беру үшін, мынадай жағдайларды қарастырайық.

Мысалы, егер 1 - ші теңсіздіктегі 400 сағат уақытты толық пайдаланып А - затын жасайтын болсақ, онда X ₁ = 1000 дана болады. (X ₁ = 400/0, 4 = 1000), бұл жағдайда өндіріс орны 1200 мың теңге (Z = 1, 2 · 1000) пайда табар еді. Бірақ мұндай пайда табу үшін ІІ - және ІІІ - топтағы станоктардың уақыты жете ме жоқ па? Соны тексеріп көрелік, өйткені А затын жасау үшін барлық үш станок та жұмыс істеу керек. Екінші теңсіздіктен X ₁ = 360/0, 9 = 400 дана. Олай болса одан табылатын кіріс 480 мың теңге (Z= 1, 2 · 400) . Сонымен қатар 1 - ші топтағы станок 400 дана А - затын жасауда (0, 4 · 400 = 160 сағат) 160 сағат, ал ІІІ топтағы станоктың барлық уақыты (8 · 400 = 3200) толық пайдаланылады. Осы сияқты талдауды В заты үшін қарастыруға болады (егер тек В заты жасалады десек, X ₁ =0) . Бұл жағдайда 3 - ші теңсіздікті пайдалансақ X ₂ =3200/4, 0= 800 дана, алатын пайда Z = 4, 8 · 800 = 3840 мың теңге болар еді, бірақ бұған 1 - топтағы станоктың 1200 сағат, ІІ - топтағы станоктың 600 сағат уақыты жетпейді. Демек, есепті бұлай шығаруға болмайды, тек біз В затынан 200 дана ғана жасай аламыз (Х ₂ = 400/2, 0 = 200) . Бұл варианттағы алатын пайда Z = 4, 8 · 200 = 560 мың теңге болады, бірақ ІІ топтағы станоктың 120 сағат, ал ІІІ топтағы станоктың 2400 сағат уақыты қолданылмай қалады.

Қарастырылған екі жағдайдың екеуі де (X ₁ =400, X ₂ = 0, Z = 480 мың теңге, немесе Хı = 0, X ₂ = 200, Z= 560 мың теңге) тиімді шешім бермейді, өйткені станоктардың пайдаланылмаған уақыты көп, демек бұдан да басқа тиімді шешім болуға тиіс. Ол шешім А және В заттарын белгілі мөлшерде жасағанда табылуы мүмкін.

4-есеп. Шаруашылық бидай және қант қызылшасын өндірумен айналыспақшы. Шаруашылықта 9000га егістік жер, 110 мың еңбек күн және 30 мың центнер минералдық тыңайтқыш қоры бар. Сонымен қатар мынадай мәліметтер белгілі:

- гектарына бидайдан 20 ц, ал қызылшадан 300 ц өнім алу жоспарланған;

- көрсетілген өнімді алу үшін 1 га бидай егетін жерге кем дегенде 1, 5 ц, ал қызылшаға 10 ц минералдық тыңайтқыш қажет;

- бір гектар жерге бидай егу үшін 4, ал қызылшаға 40 еңбек күні қажет;

- бір гектар жердіғ бидайын өсіруге және өнімді өткізуге 40 мың теңге, ал қызылшаға 560 мың теңге қаржы керек.

- бидайдың мемлекеттіксату бағасы 1 ц - 9 мың теңге, ал қызылша - 4 мың теңге.

Осы жоғарыда берілген мәліметтерді пайдаланып 9000 га жердің қанша бөлігіне бидай және қант қызылшасын өсіріп өндіргенде шаруашылық көп пайда табатын жоспар құрайық.

Есепті шешу үшін алдымен бір гектардан алынатын пайданы есептейік. Егер 1га жерден 20 ц бидай өнімін алатын болсақ, онда 1 га жерден алынатын ақша 20 · 9 = 180мың теңге. Ал бір гектар жердегі бидайды өндіру және оны өткізуге кететін шығын 40 мың теңге болса, онда бір га жерден өндірген бидайдан табатын пайда:

n = 180-40 = 140 мың теңге.

Сол сияқты қант қызылшасынан алынатын пайда:

n = 300 · 4 - 560 = 640 мың теңге.

Берілген есептің математикалық моделін құру үшін мынадай белгісіздерді қабылдайық:

Хı - бидай егіп өндіруге керекті жердің ауданы, га;

X ₂ - қант қызылшасын егіп өгдіруге керекті жердің ауданы, га;

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.