Жүк тасымалдау тиімді моделдеу

Жоспар

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .5
1 НЕГІЗГІ БӨЛІМ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...9
1.1 Жүк тасымалдау тиімді моделдеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... .9
1.1.1 Алғашқы таяныш шешімді анықтау ... ... ... ... ... ... ... ... ... ... ... ... .10
1.1.2 Тиімді шарттарын тексеру.. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..13
1.1.3 Бір жоспардан екіншісіне ауысу ... ... ... ... ... ... ... ... ... ... ... ... ... ...14
1.2 Жүк тасымалду әдісі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 17
1.2.1 Жүк тасымалдау алгоритмінің негізгі кезеңдері ... ... ... ... ... ... ... 25
2 ТӘЖІРИБЕЛІК БӨЛІМ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 27
2.1 Есептін қойылымы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 27

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .30
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ... ... ... 31

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

Кіріспе

Математикалық бағдарламалау ғылым саласы және оқу пәні ретінде
кейінірек пайда болған; күрделі экономика есептерін шешу қажеттілігі,
үйлесімді шешімдер жиынынан ең тиімдісін (оптималь) таңдау және басқалар
математикамен есептеу техникасын экономика саласына еңгізуші себепші
болады. Бұл математикалық экономиканың немесе математикалық
бағдарламалардың пайда болуына әкеледі.
Мысалы: ауыр өнеркәсіп заттарын шығаратын кәсіпорындар мен
ауылшаруашылығы өнімдерін шығаратын өндіріс салаларында басқару немесе
жоспар құру жұмыстары бір- біріне ұқсас бола бермейді. Соған қарамастан
өндірістің әр түрлі саласында кездесетін көптеген экономикалық процестер
мен құбылыстардың түпкі құрылымдарында белгілі ұқсастық қасиеттер
болады.Бір жағынан әр шаруашылықтың шығаратын өнімнің түріне байланысты
болатын болса, ал екінші жағынан тұтынатын шикізатының түріне өндірістік
қатынастары мен қоршаған ортасының ерекшеліктеріне байланысты. Мысалы:
жоғарыда аталған өндіріс салаларында шығарылатын өнімдердің түрлерінде
ұқсастық болғанымен, сол өнімдерді шығару барысында кездесетін шектеулі
қорларды тиімді бөлу порцестерінде ұқсастық қасиеттер болуы мүмкін. Міне
осындай кейбір қасиеттерінде ұқсас белгілері бар экономикалық процестерді
топтастыра алсақ, онда олардың математикалық модельдері де бір- біріне
ұқсас болып келуі де мүмкін. Өндірістік процестерді зертеуде кеңінен
қолданылатын тәсілдердің бірі – сызықтық программалау. Сызықтық
программалау дегеніміз өндірістік негізгі мақсаты мен шарты белгілі бір
сызықтық өрнектер немесе теңдеулер түрінде берілген жағдайларда сол
процестерді зерттеу үшін қолданылатын матрицалық тәсіл.
Экономика ғылымының әрі қарай дамуына қажетті шарттарының бірі сандық
анализдің нақты әдістерін қолдану және математиканы кеңінен қолдану.
Қазіргі уақытта математика мен қазіргі заманға есеп технологиясының
жетістіктері экономикалық зерттеулер мен жоспарлауда кең қолданыс табуда.
Бұл математика, математикалық программалау сияқты, ойын теориясы,
көпшілікке қызмет ету теориясы және де тез әрекеттегі электронды есептеуіш
техникасының толқынды дамуы бөлімдерінің дамуына ықпал етеді.
Математикалық әдіс арқылы экономикалық есептерді шешу және орнатуда
едәуір нәтиже жинадық. Әсіресе оптимальды жоспарлау әдісі табысты дамуда,
бұлар математикалық программалаудың мәні болып табылады. Негізгі болып
оптимальді жоспарлаудың бірыңғай жүйесін құру есебі және халық шаруашылығын
басқаруды математикалық әдіспен және электронды есептеуіш технологиясын
экономикада қолдану.
Экстремалды экономикалық есептерді шешуді мынадай 3 этапқа бөлуге
болады:
1. Экономика-математикалық модельді құру;
2. Белгілі бір математикалық метод арқылы оптимальді шешімді табу;
3. Халық шаруашылықтарына экономикалық және өндірістік процестердің
нұсқасын енгізу.
Экономика - математикалық модельді құру, біріншіден, зерттелінетін
экономикалық процесстің математикалық моделін құруы, ол оның мәнін
көрсететін құрылымы. Басқа сөзбен айтқанда, мұндай модельде есептің
маңызды өзгешелігі есептелуі керек және де шек қою шарттары, олар нәтижеге
ықпал етуі мүмкін.
Математикалық программалаудың құрама бөлімдері сызықты, сызықты емес
және динамикалық программалау болып табылады. Бірінші рет сызықтық
программалау есебінің орнатылуы совет экономисті А.Н. Толстойдың (1930 ж)
жұмысында берілген. 1931 ж. Венгрлік математик Б. Эгерварн математикалық
құрылымды қарастырып, сызықты программалаудың есебін шешті, ол таңдаудың
келелі мәселесі деп атқа ие болды, шешу әдісі венгерлік әдіс деген ат
алды. Шешім шығару жолдардың жарату мүмкіндіктері болады, ол алгоритмдердің
шешім шығару үшін электрондық есептеуіш машиналарын есептерге қолданады.

Мұндағы басты рольді математикалық модельдеу атқарады.
Математикалық модельді құру үшін зерттеліп жатқан жүйенің функционалдық
мақсатын білу және шектеулер туралы мәліметтер қоры болуы қажет.
Операцияларды зерттеудің негізгі мақсаты ол берілген тапсырмаларды
шешудегі әдістердің ең жақсысын анықтау болып табылады.
Мақсаты және шектеулері функция түрінде ұсынылуы қажет Осы курстық
жобадағы жұмыс арқылы біз өзіміздің Потенциалдар әдісі пәнінен
алған білімімізді бекітуге өз көмегін көрсетеді.
Қазіргі таңда ғылым кәсіпорындар мен басқару бөлімдеріне
көп көңіл бөліп, ол бізді көзге көрінерлік структуралары мен
кәсіпорын сияқты бағытталған қиын процесстерді анализдеуге
итермелейді. Тәжірибенің керектігі өмірге арнайы әдістерді
алып келіп, оларды бір атпен операцияларды зерттеу деп
атады. Бұл терминмен біз математикалық, сандық әдістерді
бағытталған адам өміріндегі барлық шешімдерді қабылдау деп
түсінеміз.
Ауыспалы операцияларды зерттеу әдісінде оларға бағынышты шектеулер мен
мақсатты функция дискретті (көбінесе толық санды) және континуальды
(үздіксіз) болуы мүмкін. Сонымен қатар, шектеулер мен мақсатты функция
сызықтық және сызықтық емес болып бөлінеді. Осы модельдерді шешудің
әртүрлі әдістері бар, олардың ішіндегі ең әйгілісі және қолайлысы сызықтық
программалау әдісі., онда мақсатты функция және барлық шектеулер сызықты.
Математикалық модельдеудің басқа түрлерін шешу үшін динамикалық
программалау, толық санды программалау, сызықтық емес программалау
әдістері, көпкритерийлі оптимизация және желілік модельдеу әдісі
қолданылады.
Табиғи итерационды алгоритмдер көбінесе бір түрлі көлемді шешімге
келеді. Сондықтан бұл алгоритмдер есептеуіш техника көмегімен орындау
негізінде өндіріледі. Операцияларды зерттеудің барлық әдістері есептік
алгоритм туғызады деуге болады. Олар табиғи итерационды болып
келеді. Ол тапсырма кезекті (итерационды) шешіледі, яғни қадам
(итерация) сайын шешім табамыз, сонымен оптимальды шешімге
келеміз.
.

1 НЕГІЗГІ БӨЛІМ

1.1 Жүк тасымалдау тиімді моделдеу

Қарапайым экономика есептерінің модулдерін құрастыру кезінде тасмалдау
(жүк тасымалдау есептер) моделдері келтірімді. Мысалы: қалалар мен
ауылдарды жобалау жұмыстарында немесе әртүрлі өндіріс мекемелерін ел
мекемелеріне орналастыру туралы есептерді шешу кезінде математикалық
формулалар кездестіруге болады. Тасмалдау есебі сызықтық бағдарламалау
есебіне жатады. Оны шешу үшін симплек әдісін пайдаланамыз. Бұл есепті шешу
үшін арнайы потенциалдар әдісін пайдаланамыз. Осы әдісті қарастырайық. Жүк
тасымалдау тиімді әдісін пайдалану үшін тасмалдау есебінің тек жабық
моделін қарастыруға тиіс. Өндірістік процесстерді зерттеуді кеңінен
қолданылатын тәсілдердің бірі – сызықтық программалау. Сызықтық
программалау дегеніміз - өндірістің негізгі мақсаты мен шарты белгілі
бірсызықтық өрнектер түрінде берілген жағдайда сол процессті зерттеу үшін
қолданылатын математикалық тәсіл. Математика тілімен айтқанда сызықтық
программалау дегеніміз – белгісіздеріне сызықтық тең сызықтар түрінде шарт
қойылған сызықтық функцияның ең үлкен немесе ең кіші мәндерін табатын
ғылым. Сызықтық программалау есебінің жалпы түрі.
Жалпы жағдайда, алғашқы таяныш жоспар табылған соң, транспорттық
есебінің оптимал шешімін симплекс әдісі арқылы табуға болады. Бірақ,
транспорт есебінің ерекшеліктерінен туатын кейбір қиыншылықтарға байланысты
(есептің шарты теңдеулер системасы түрінде берілетіндіктен , әрбір белгісіз
тек екі теңдеуге енетіне байланысты, белгісіздердің коэффиценттері бірге
тең болуы себепті) симплек әдісін пайдалану қолайсыз болады. Сол себепті,
транспорт есебін шығару үшін арнаулы әдістер қолданылады.
Бүгінгіде кеңінен қолданылып жүрген осындай бір әдісті 1949 жылы совет
ғалымдары Л. В. Канторович пен М. К. Гаврун ойлап тапқан. Ол әдісті
потенциалдар әдісі деп атайды. Потенциалдар әдісінің жәрдемімен, алғашқы
таяныш жоспардан саны шектеулі интерация жасай отырып транспорт есебінің
оптимал шешімін табуға болады.
Әдістің алгоритмінің негізгі кезендері мынадай:
- алғашқы таяныш шешімді табу;
- табылған шешімінің тиімді екендігін тексеру;
- бір шешімнен екіншісіне өту.
Егер екінші кезенде тиімді шарттар орындалған жағдайда есепті шешу
процесі тоқтатылады, ал ол шарттар орындаласа, онда үшінші кезең орындалуға
тиіс. Екінші және үшінші кезеңдердің әрбір қайталануын итерация деп атайды.
Ырғақты қайталама саны алдын – ала белгілі болмайды. Ол тиімді шешім
табылғанша немесе оның болмайтындығына көз жеткізгенше қайталанылады.

1.1.1 Алғашқы таяныш шешімді анықтау

Тасымалдау есебінің алғашқы таяныш шешімін анықтау әртүрлі жолмен
орындалуы мүмкін. Олардың ең көп тарағандары:
А) солтүстік-батыс бұрыш және
Б) ең кіші элемент тәсілдері.
Осы тәсілдердің қолдану тәртібін қарастырайық.

Солтүстік-батыс бұрыш тәсілі
Бұл тәсіл бойынша тасымалдау есебінің үлестіру кестесі оның жоғары сол
жақ бұрышынан бастап толтырыла бастайды. Мұндағы негізгі тәртіп
формулаларға сәйкес тік жолдармен жатық жолдардағы сандардың қосындыларының
bj мен ai-ге тең болуы.
Айтылған тұжырымдар түсінікті болуы үшін мысал қарастырайық.

1.1.1.1 – кесте. Мысал
Қойма Тұтынушылар Жүк қоры
В1 В2 В3 В4 В5
А1 8 2 8 3 6 150
-0 +0 0 0 0
10 50
А2 2 8 4 7 6 240
0 -0 90 90 0
0 60
А3 4 3 2 4 8 140
0 0 0 10 130
Қажеттілік 100 110 90 100 130 530
530

Бұл тасымалдау кестесінің толтырылу тәртібі мынадай. Алдымен ең
жоғарғы сол жақтағы бұрыштағы кереге көзге 100 деген сан жазылады; оның
себебі А1 қоймасында 150 мөлшерінде жүк қоры болса, ал В1 пайдалануға
қажетті 100; сондықтан х11=100. одан артылған 50 мөлшердегі жүк екінші
пайдаланушыға беріледі, немесе х12=50, ал қалғандары 1-ші қоймадан жүк
алмайды, немесе x13=x14=x15=0. сонымен қатар 1-ші пайдаланушы В1 өз
қажеттілігін толық қамтамасыз еткендіктен басқа қоймадан жүк алмайды,
немесе x21=x31=0.
Осыдан кейін келесі толтырылған кереге көз 2-ші жатық жол мен 2-ші тік
жолдың қиылысында орналасқан. Мұнда екінші пайдаланушыға В2 қажеттегі 60
мөлшердегі жүк берілуі тиіс, немесе х22=60. Сонда ол өз қажеттілігін түгел
қамтамасыз етеді; немесе х32=0.
Осылайша қайталанып отырып, кестенің барлық кереге көздерін толтыруға
болады. Сонымен, (2.11) – (2.14) шарттарын қанағаттандыратын мынадай шешім
немесе тасымалдау жоспарын құрастыруға болады:
X11=100; X12=50; X13=0; X14=0; X15=0;
X21=0; X22=60; X23=90; X24=90; X25=0;
X31=0; X32=0; X33=10; X34=10; X35=130;
Бұл жоспарды орындауға жұмсалатын қаржы мөлшері былайша анықталады:
F=8*100+2*50+8*60+4*90+7*90+4*10+8* 130=3450

Ең кіші элемент тәсілі
Жоғарыда қарастырылған тәсіл бойынша үлестіру тасымалдауға жұмсалатын
қаржыны есепке алмайды. Ол үшін ең кіші элемент тәсілін пайдалануға болады.
Ең кіші элемент тәсілі бойынша кестеден ең кіші элемент орналасқан кереге
көзді толтырудан бастаймыз; ал қалғандары жоғарыда көрсетілген тәсілдерден
(2.12)-(2.14) шарттарының орындалуын қамтамасыз етуге тиіс. Жоғарыдағы
мысалды қарастырайық.

1.1.1.2-кесте. Мысал
Қойма Тұтынушылар Жүк қоры
В1 В2 В3 В4 В5
А1 8 2 8 3 6 150
0 40 0
0 110
А2 2 8 4 7 6 240
10 0 130
100 0
А3 4 3 2 4 8 140
0 0 80 60 0
Қажеттілік 100 110 90 100 130 530

Бұл есептегі ең кіші элемент 2-ге тең; ол үш рет кездеседі; олардың
кез-келгенінен бастауға болады. Біз бірінші жолда орналасқанынан бастайық.
Кестенің осы кереге көзіне 110 санын жазамыз, немесе екінші пайдаланушы В2
өзіне қажетті барлық жүкті бірінші қоймадан ең арзан қаржы жұмсап алады,
немесе х12=110; ол басқа қоймадан жүк алмайды: x21=x32=0.
Бірінші қоймада қалған 40 мөлшердегі жүк төртінші пайдаланушыға
беріледі, себебі оның жұмсайтын қаржысы басқасынан аз. Осылайша кестенің
барлық кереге көздерін толтыруға болады. Сонда мынадай жаңа жоспар (шешім)
пайда болады:
X11=0; X12=110; X13=0; X14=40; X15=0;
X21=100; X22=0; X23=10; X24=0; X25=130;
X31=0; X32=0; X33=0; X34=60; X35=0;
Бұл жоспарға жұмсалатын қаржы мөлшері:
F=2*110+3*40+2*100+4*10+2*80+4*60+6 *130=1760
Осы тәсіл бойынша анықталған жоспар солтүстік батыс бұрыш тәсілінен
пайдалырақ екенін көруге болады.
Ескерту. Тасымалдау кестесін толтыру кезінде толтырылған (хij≠0)
кереге көздер саны n+m-1-ге тең болуы керек.

1.1.2 Тиімді шарттарын тексеру

Табылған шешімнің тиімді екендігін тексеру үшін келесідей амалдарды
орындау керек:
а) Жүк қоймалары мен оны алушылардың потенциалдарын еңгізейік: U1,
U2,..., Un және V1, V2, ..., Vm.
б) Тасымалдау кестесінің әрбір толтырылған кереге көзі үшін UI (i=1,n)
және Vj (j=1,m) белгісіздері бойынша n+m-1 теңдеулер жүйесін құрастыру
керек:
Vj-Ui-Cij=0.
(1.1.2.1)
в) Осы құрастырылған теңдеулер жүйесін шешу арқылы Ui және Vj
белгісіздерінің мәндері анықталады.
г) Кестенің толтырылмаған кереге көздері үшін келесе шарттың орындалуы
тексеріледі:
Vj-Ui-Cij≤0
(1.1.2.2)
Егер осы (1.1.2.2) шарт барлық кереге көздер үшін орындалса, онда
есептің шешімі тиімді болғаны; ал керісінше жағдайда тиімді болмайды.
Осы айтылған амалдардың іс жүзінде орындалуын көрсету үшін жоғарыда
келтірілген есептің солтүстік-батыс бұрышы тәсілі бойынша табылған шешімін
қарастырайық.
Бұл кесте үшін қарастырылатын теңдеулер жүйесі былайша жазылады:

V1-U1-8=0 V4-U2-7=0
V2-U1-2=0 V4-U3-4=0 (1.1.2.3)
V2-U2-8=0 V5-U3-8=0
V3-U2-4=0
Мұндағы белгісіздер саны теңдеулер санынан бірге артық. Сондықтан
белгісіздердің біріне кез-келген мән беру арқылы осы жүйенің шешімін табуға
болады. Мысалы:
U1=0; V1=8; V2=2; U2=-6;
V3=-2; V4=1; U3=-3; V5=5. (1.1.2.4)
Енді (1.1.2.2) шарттың орындалуын тексерейік. Ол үшін кестенің бос
терезе көздерін (хij=0) қарастырамыз; олар үшін келесі өрнектердің
мәтіндерін анықтаймыз:
V3-U1-8=-10; V5-U2-6=-5;
V4-U1-3=-2; V1-U3-4=7;
(1.1.2.5)
V5-U1-6=-1; V2-U3-3=2;
V1-U2-2=12; V3-U3-2=-1.
Осы қарастырып отырған есептің солтүстік-батыс бұрыш тәсілі бойынша
табылған шешімі тиімді еместігі дәлелденді. Оның себебі (1.1.2.5)
өрнектеріндегі үш мән немесе тиімді шартына (1.1.2.2) қарама қайшы.

1.1.3 Бір жоспардан екіншісіне ауысу

Егер табылған шешім тиімді шарттарды қанағаттандырмаса, онда басқа
шешімді қарастыру қажет. Потенциалдар әдісі бойынша бір жоспардан
екіншісіне ауысу белгілі бір тәртіппен орнатылады:
а) Кестенің бос кереге көздері үшін анықталған Vj-Ui-Cij өрнегінің ең
үлкен оң мәні орналасқан кереге көзді де таңдап,оған барынша үлкен мән
жазуға тырысамыз. Бұл жерде xij≥0 шартының орындалуын ұмытпау қажет).
б) Таңдап алынған кереге көзге жазылған мәнге байланысты басқа кереге
көздерде өндірістер еңгізілуге тиіс.
Осыдан кейін есептің жаңа шешімі немесе тасмалдаудың жаңа жоспары
пайда болады.
Мысал ретінде қарастырылып отырған есептің тиімді еместігіне көзіміз
жеткен шешімнен басқа шешімге өту жолын қарастырайық.
Тиімді шарттардың орындалуын тексерген кезде (1.1.2.5) өрнектерінің
ішіндегі ең үлкен оң сан (12) екінші жатық жол (i=2) мен бірінші тік жолдың
(j=1) қиылысына орналасқан.
Осы кереге көзге барынша үлкен сан жазылуға тиіс. Әзірше оны 0-ге тең
деп алайық: х21=0. Сонымен бірге кестенің басқа кереге көздерінде де
өзгеріс болуға тиіс. Себебі оларда теңдіктер сақталуы тиіс, немесе:
X11=100-0; X12=50+0; X22=60-0;
X23=90; X24 =90; X34=10; X35=130
Мұндағы 0-ның мәнін табу үшін 2 шарт орындалуға тиіс: біріншіден, ол
барынша үлкен болуға тиіс, 2-ден (6) өрнектерінің мәндері теріс болмауы
керек. Оны оңай табуға болады: 0=60;
Осылан кейін жаңа жоспарды немесе есептің жаңа шешімін былайша жазуға
болады.
X11=40; X12=110; X13=0; X14=0; X15=0
X21=60; X22=60; X23=90; X24=90; X25=0
X31=0; X32=0; X33=0; X34=10; X35=130

Бұл жоспарды орындауға жұмсалатын қаржы:
F=8*40+2*110+2*60+4*90+7*90+4*10+8* 130=2730
Есептің ең кіші элемент тәсілі бойынша табылған шешімі үшін де тиімді
шарттардың орындалуын тексеруге болады. Ол үшін потенциалды анықтаудың
теңдеулері құрастырып, шешімін табамыз.
V2-U1-2=0; U1=0;
V4-U1-3=0; V2=2;
V1-U2-2=0; V4=3;
V3-U2-4=0; V3=1;
V5-U2-6=0; U3=-1;
V3-U3-2=0; U2=-3;
V4-U3-4=0; V1=-1; V5=3
Тиімділік шартты тексереміз.
V1-U1-8=-9 V4-U2-7=-1
V3-U1-8=-7 V1-U3-4=-4
V5-U1-6=-3 V2-U3-3=0
V2-U2-8=-3 V5-U3-8=-4
Бұл шешім тиімді шарттарды қанағаттандырады.
Сонымен жабық модель күйінде берілген тасмалдау есебінің потенциалдар
әдісін шешудің барлық кезеңдері қарастырылады.

1.2. Жүк тасымалдау тиімді әдісі

Теорема 1.
Егер х=(хij) жоспары транспорт есебінде оптимальды болса, онда оған
m+n систимасы сәйкес келеді.Ui және Vj саны мына шартты қанағаттандырады.
Ui+Vj=Cij үшін xij0
Және
Ui+VjCij үшін xij=0
(i=1.2 ... m; j=1.2 ... .n).
Ui және Vj саны тұтынушы мен жабдықтаушыларға сәйкес потенциалдар саны
деп аталады.
Дәлелдеу
Транспорттық есептің кішірейтілген сызықтық функциясы Z=
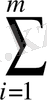
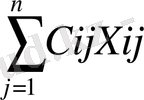шексіздігі ретінде
xi1+xi2+...+xin=ai, i=1,2,...,m,
x1j+x2j+...+xmj =bj, j=1,2,...,n,
xij≥0 (i=1,2,...,m; j=1,2,...,n)
кезкелген шығару есебін сызықтық бағдарламада қарастыруға болады.Егер
әрбір шексіздік xi1+xi2+...+xin=ai түрінде болса, онда шығару нәтежиесінде
Ui(i=1,1,...,m) айнымалысына сәйкес келеді. Ал кезкелген xij=x2j+...+xmj=bj
шексіздік түріне Vj(j=1,2,...,n) айнымалысы, ол нақты максимумдалған сызықтық
функция f=+;
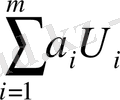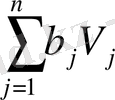Ui+Vj≤Cij(i=1,2,...,m;j=1,2,...,n)-ге шекгелген.
Х жоспары 2 еселенген оптималды тапсырма жоспары, сондықтан Y=(Ui,Vj)
жоспары шығару тапсырмасының және 2 еселенген теореманың түбірі max f =
min немесе
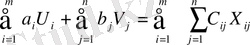, мұндағы хij≥0.
Тапсырманың шексіздігіне сәйкес келетін оптималды жоспардың 2
еселенген тапсырмасына қатаң теңдіктің қанағаттандырылуы және сәйкес
келетін компоненттер 0-ге тең теңсіздігі сияқты т.с.с.
Ui+Vj=Cij үшін xij=0
Ui+Vj≤Cij үшін xij=0
Дәлелденген теоремада тірек жоспары оптималды болуы үшін мынадай
шарттар орындалуы тиіс:
а) әрбір толтырылған ұяшықтар үшін потенциалдар суммасы тасмалдаушы
бірлігіне тең немесе одан аз, мына ұяшықтағындай болуы тиіс.
Ui+Vj+Cij;
б) әрбір бос ұяшықтағы потенциалдар суммасы тасмалдау бірлігіне тең
немесе одан аз, мына ұяшықтағындай болуы тиіс.
Ui+Vj≤Cij.
Егер толтырылмаған бос ұяшықшартты қанағаттандырмаса, онда тірек
жоспары оптималды емес және оны жақсартуға болады. Векторды базиске
кіргізіп, сәйкес келетін ұяшықта оптималдық шарты орындалмайды (т.с.с.
ұяшыққа кейбір жүк бірлігінің сандарын сыйыстыру керек).
Мұндай әдіспен жоспарды тексеру үшін ең бірінші потенциалдар жүйесін
құру қажет.Потенциалдау әдісінің алгоритімін және сонымен бірге тірек
жоспарында қарастырамыз.
1.Потенциал жүйесін құру.
Потенциал жүйесін құру үшін Ui+Vj=Cij шартын қолданамыз. Мұнда Cij-j
бағаны және i жолының толық ұяшығындағы жүк бірлігінің құны.
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.