Қызмет көрсету жүйелерін модельдеу және кезек теориясының негіздері


Кіріспе
Жүйенің өздігінше сараптамамен жұмыс іздеуін жиі кездестіруге болады.
Жалпы қызмет көрсету жүйесі бірканалды немесе көпканалды болады. Кез келген СМО тапсырысқа қызмет етуге негізделген, жалпы айтқанда СМО-ға келіп түсетін уақыттың кездей соқ мезетінде келіп түскен тапсырысқа қызмет көрсету бір уақыт мерзімінде жалғасады, одан киін конал босайды және келесі тапсырысты қабылдауға дайын болады. Кездейсоқ мінездеме легінің тапсырысы мынадай жағдайға әкеліп соғады, тапсырыс саны бір уақыт мерзімінде жиналып көбейіп кетеді (олар негізінде кезекке тұрады немесе СМО -дан қызмет көрсетілмей босатылады) ; келесі мерзімдерде СМО жұмыс істемей тұрып қоиаы. Лек немесе жағдай легінің түсінігі үрдістің қызмет көрсету талабына сай жүргізіледі және жүйенің талабына қызмет көрсету үрдісінің келіп түсуін бейнелейді. Лек деп жағдайдың жалғасуын айтады.
Егер де интервал уақыты ағымның жағдайына сәйкес болса, ағым үздіксіз болып аталады. Ал егерде оның кездейсоқ жағдайлары уақыт мезетінде болып жатса ағын кездейсоқ болып табылады. Кездейсоқ ағым кездейсоқ вектор болып көрсетіледі. Ағымдардың маңызды мәселесі, стационарлы шарттарын толықтыру, қанағаттандыру.
Кездейсоқ ағым кез келген n санының пайда болуы туындалса уақыт интервалы (t, t+T) уақытша оның алдынғы t -ға тәуелді болмаса стацианарлы болып табылады . Жалпы көрсетудің әр жүйесі өндірілуіне және конал санына байланысты, сонымен қатар тапсырыс ағымының мінездемесіне байланысты ерекше қасиеті бар. Жалпы қызмет көрсету теориясының пәні - қызмет көрсету ағымының мінездемесі арқылы бекітілген, конал санының өндірілуіне, СМО -ның жұмыс ережелеріне сай қызмет көрсету. Қызмет көрсетудің мінездемеге сай эфектісі, міндет пен мақсат шартына байланысты тексертіледі, әр түрлі үлгілер мен функциялар қолдануға болады, мысалы:
-СМО-да уақыт бірлігіне қызмет көрсете алатын тапсырыстың орташа саны,
-Қызмет көрсетілмей СМО-ны босатып тапсырыстың орташа проценті.
-Келіп түскен тапсырыс тез қабылданып қызметке кіріседі.
-Кезекте күтудің орташа уақыты.
-Күту уақытын орналастыру заңы.
-Кезекте тұлған тапсырыстың орташа көлемі .
-Кезектегі тапсырыс санын орналастыру заңы .
-Уақыт бірлігінің жалпы қызмет көрсету жүйенің әкелген орташа шығыны м. с. с.
Тапсырыс легінің кездейсоқ мінездемесі, жалпы жағдайда қызмет көрсетудің созылуы мынандай жағдайға әкеліп соғады, онда кездейсоқ үрдіс жалпы жүйесі қызмет көрсетіліп жатады. СМО-ға нақты талапты міндеттеу және сол үрдістің өндіріс рационалы біршама кеңес беру үшін, жүйе ағымындағы кездейсоқ үрдісті математикаға сай түсіндіру маңызды. Жалпы қызмет көрсету теориямен айналысады. Технологиялық тқрақтылық сараптамада бірдей міндеттер туындай бастайды . СМО -ның математикалық анықтаманың жұмыс атқаруы олайда кеңейеді, егерде ол марковті кездейсоқ үрдіс жүйе ағымында болса. СМО-параметірлерге тәуелді болуы үшін қызмет көрсету эффектісінің негізгі мінездеме көрсеткішіне сай және СМО математикалық түсінімнін құрастыру жеткілікті. Ол үшін үрдіс, жүйе ағымында марковті болуы үшін, керектісі барлық лектің желілері жағдайдың жағдайдағы жүйеге ауысуы, еш кедергісіз пуассанальді легі болуы қажет. СМО - ға лектің желілері - ол лектің қызмет көрсетілуі және тапсырыс лектері. Егерде бұл лектер пуассональді болмаса, үрдістің математикалық көрсеткіші, СМО -да болып жатқан математикалық аппаратты көбірек талап етеді, тек кездейсоқ жай жағдайларда ғана оларда аналитикалық формуланы алу мүмкіндігі бар. СМО жұмысын үздіксіз уақытпен және дискретті жағдайдың кездейсоқ үрдісі біршама қарастыруға болады: жаңа тапсырыстың келуі желінің аяқталу барысында көтеріліп СМО -ның жағдайы ауысады, жүйенің уақыты көрсетілмеген қызмет немесе көрсетілген қызметінің аяқталуы. (төменде қараңыз) . Онда соған байланысты үздіксіз уақытта марковский үрдістің болып жатқанындай, шекті стационарлы мезеті СМО -да уақыт ағымы арқылы тұрақтыланып, уақыттың тәуелсіз мінездемелерінде біркелкі бейнеленеді. Модельдеу барысында негізгі мәселе туындау және СМО стационарлық мезетінің мінездемесі нақ осылар болып табылады. Кездейсоқ тәжіребелі мәселеде СМО -ның морковсіз ауысым мезетіндегі аналитикалық модельдерін алуға мүмкіндігі болмағанына қарамастан, стационарлық мезеттің туындыларына аналитикалық шешімі болады, негізінде жалпы мінездемеге байланысты. Мысалы бұл жерде жалпы теорияның қызмет көрсету барысында үлкен роль атқаратын Литтланың керемет формуласын келтіреміз. (Дәлелсіз) .
Мейлі λ - интенсивті лек тапсырысында, жүйеге келіп түсетін және стационарлы мезетте негізгі тұрақтыланған жүйеде негізгі мінездемеленген болса:
-Орташа санмен
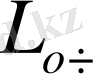 және орташа уақытпен болған
және орташа уақытпен болған
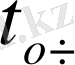 тапсырыс кезегі;
тапсырыс кезегі;
-Орташа санмен
 және орташа уақытпен болған
және орташа уақытпен болған
 толық тапсырыс жүйесі . Ендеше тапсырыс келгенде уақыт пен мезет аралығында кез келген орналастыру, қызмет көрсетудің кез келген дисциплинасы және кезкелген қызмет көрсетудің уақыт орналастыруы:
толық тапсырыс жүйесі . Ендеше тапсырыс келгенде уақыт пен мезет аралығында кез келген орналастыру, қызмет көрсетудің кез келген дисциплинасы және кезкелген қызмет көрсетудің уақыт орналастыруы:
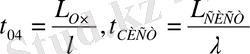 .
.
Келесіде қызмет көрсетудің жалпы элемент теориясы нақты бөлмекте көрсетіледі.
1 НЕГІЗГІ БӨЛІМ
1. 1 Көпшілікке қызмет көрсету жүйесін модельдеу
Қазіргі кезде ғылым мен техниканың даму денгейі, ертеректе пайда болған белгілі ресурстар, іс-шаралар масштабтардың құны мен салдарын іске асыруды жоспарлайды. Ірі масштабты іс-шараларды іске асыру тәуекелі бүгінгі таңда технология мен техниканың ауысымымен тереңдетіледі. Нәтижесінде техника мен әдетте қолдану адам өмірінде бірнеше рет ауысып отыруы тиіс. Яғни техниканы жете менгерген және онымен жұмыс істей алатын адамдар қалыптасып үлгермейді. Сондықтан қазіргі таңда сынау әдісі мен қателесу қолданысқа кірмейді: қателесудің зардабы қауіпті және сынауға да өте аз уақыт берілген. Қазіргі таңда бұрынғымен салыстырғанда өз бетімен еркін шешім қабылдау аз екендігі анық көрінуде.
Жоспар бойынша бірінші мекеме мен басқарманың келесі мәселесі, оның ішінде машинаны басқарудың ғана емес, адамның машина жүйесін басқаруы болып отыр. Ал бұл алдын ала есептелуі негізінде жауапты шешім қабылдауды білдіреді. Сондықтан да қазіргі кезде математикалық әдістердің барлық жаттығу облыстарында өсуінің байқалуы кездейсоқтық емес: нақты объектілерге қатысты санап көру мен қателесудің орнына модель жасау тиімдірек. Операцияны зерттеуді қалыптастыруды алдын-ала шешімге сүйеніп барлық облыстарға бағытталған қызметте математикалық аппаратты кеңінен қолданатын ғылым.
Бұл дәстүрлі облыстарда қосымша нақты және тәжірибелі ғылым-матем атика ғасырлар бойы гуманитарлық деңгейде оқытылатын сұрақтармен айналысады дегенді білдіреді. Математикалық моделдер құрылып талданады математикалық әдістер қолданылады. Математикалық моделдер бұрын богде болған облыстарға кіріп қана қоймай таратылып өзінің әдістемелік келбетін өзгертуде.
Себебі - нақты ғылымнан гөрі германиалық бағыттағы ғылымның құрамы күрделілеу. Бұл құбылыстар шарттылықта қиынырақ беріледі олардың тәуелді болу себептері анағұрлым көп және зерттеудің құрылымы верболды әдіс, яғни ол парадоксалды емес болғандықтан логикадан тиімдірек.
Математикалық құрылымға қандай орын тиесілі? Алдымен иатематикалыық әдістерді қырылымның тиімді тәсілі деп қарастыруға болады. Бұл әсіресе мағлұматтың сандық масив түрінде графикалық қалыпта берілгенде анық байқалады. Көп көлемді мағлұматты бар есептеерді шығарғанда маңызды орын алады. Сонымен қатар стандартты схемада қалыптасқан практикада тиімділігімен тексерілген үлгідегі есептер көптеп кездеседі. Сонда математикалық әдістемелер мен түсініктер дің шешімі тұрақтанады.
(XVIII-XIX ғасырларда) операциаларды зертеу мен дамуы негізгі этап болған.
XX - ғасырлардын басында математикалық модельді құру антогандық түсініспеушілікке әкелді. Ф. Харристің инвитицияларды басқару, А. Эриаттың кезек теориясы. Басқарма мәселесінің шешімін табу математикалық әдістеменің айқын өріс алуына қарамастан зерттеу операциясы ғылым ретінде тек XX ғасырда 40-50жыл ғана танылды. 11 адамнан тұратын британдық эксперттік топтың Англияға үшін шайқасының нәтижесі белгілі мысал бола алады. ”Blackett’s Circus”деген атпен әйгілі болған бұл топқа физиологтар, математиктер, физиктер, геодезист, астрофизиктер және әскерилер кірген. Көптеген басқарма тапсырмалары жақсы қалыптасып, қазіргі кезде стандартты әдістермен шешіледі.
Зерттеу аперациясының әдісін есептегіш құралдарына тәуелді деп асыра айтуға болмайды. Қазіргі таңда көптеген ірі масштапты есептерді жылдамдығы күшті компьютерлермен шешуге болмайды.
Сонымен XX ғ. бірінші жартысында басқарудың элементтерін ғылыми әдістеме негізінде шешу жолын жете зерттелді, ал сызбалар, жаратылыстану ғылымы мен инженерлі-техникалық іздеулер жүргізу лезінде жақсы көрсетіліп, оларды басқармалық есептерді шешу жолында пайдалана бастады.
Басқарма есептердің сипаты мен дәрежесі оның шешуі әдістерін іздестіріп анықтайды. Жақсы құрылған, нашар құрылғы ж/е құралмаған есептерді айырмашылығын айырады. Олардың арасында айқын қырын анықтауға болмайды. Жақсы ұсынылған схема болса кейде нашар құрылған мәселенің ар жақсы құралған стандартты есепке айналады.
АҚШ-тың 125 ірі корпорациясының басқарма есептерін шығарудағы математикалық әдістерден мен модельдерден дерек келтірейік (Guisseppi. A. Forgionne. Corporate. Management. Science. Activities: An Update, interfaces, 13(Jume1983) . P 20-23) .
1. 1. 1-кесте. Математикалық әдістер мен модельдер
Операцияны зерттеу математикалық құралдарын адамдар, машина, материал мен өнеркәсіптің ж/е іскерлік сферада, мемлекеттік басқармада, қорғаныс жүйесінде қиын шешімдерді шешуге қолданады. Оның өзіне тән ерекше құрылымы математикалық моделдің жүйесіне тән. Модель түрлі стратегиялар мен басқарудың әдістерінің нәтижесін салыстырып есептейді.
Операцияны зерттеудің басты міндеті менеджер мен басқа да адамдар үшін саясатпен істердің пайыздап алған нұсқада алдына қойылған қандай да бір мақсатқа жету үшінкөмек ретінде қолданады. Қысқаша операцияны зерттеуді мәселені шешуге арналған ғылыми тәсіл десе де болады. Келесі мәселе бір жүйедегі көңіл жалаған ж/е факт жағдайының арасындағы қатыспаушылық шешілуі-бақылаудан қажеттілікке әкелетін іс-әрекеті таңдау барысында қабылдаушылықты жеңу құралы.
Қазіргі таңда операция ұғымының астарында ортақ ниетпен біріккен мақсаттыіс-шараларды басқару, ол операцияның негізгі зерттеу міндеті осы ниеттерді жетілдіру мен іске асыру жолдары болып табылады.
Барлық операцмяларда нәтижесіне жауап беретін басшылары яғни шешім қабылдаушы адам болады. Математикалық әдістер мен операциялары сараптай ашатын топ н/е адам ерекше орын алады. Бұл топ н/е адам модельдің техникалық міндеттерді модельдеу сұранымдарына жауапты болады. Анализдің өзі шешім қабылдай алмайды, тек қана операциялау жағына ғана көмектесті. Оның хабардар болу денгейін шешіп қабылдаушы топ шешеді. Операция зерттеу барысында математикалық құрылымның қандай орын алатынын түсіндіру үшін мәселелерді шешуге болатын негізгі этаптарды ұсынамыз.
1 . Келесі мәселенің шешімі. Бұл өте маңызды нетривиалды қадам. Нақты келесі мәселенің белгілерін анықтап қана қоймай оған түсіністік, интуицияны талап етеді.
2 . Модельді таңдау. Егер мәселе дұрыс құрылған болса, жаңа модель болмаса, онда мәселенің айқын жағынан көрсететін модель жасау керек болады.
3 . Шешімін іздеу. Шешімін табу үшін нақты деректер қажет, жинақтау мен дайындау біріккен күшті талап етеді.
4 . Шешімді тестілеу. Алынған шешім міндетті түрде қолдануға болатындылығы тиісті тест арқылы тексеріледі. Қанағаттанарлықсыз шешім модельдің мәселенің анық табиғатын көрсетпейді. Бұл жағдайда ол не жетілдірілу қажет, болмаса сәйкес келетін модельге ауыстырылу қажет.
5 . Бақылауды ұйымдастыру. Егер табылған шешімді қолдануға болатын болса, ж/е модель бірегей ғана жағдайларды шешуге ғана пайдаланып қана қоймай, болашақта ұқсас жағдайларды қарастыратын болса, моделді дұрыс қолдануын тексеріп отыратын механизмді тарату керек болады.
6 . Орайлы режим жасау. Бұл қадам ең қиыны жаңалық еңгізу қызығушылықтың болмауы ғана емес оның қарсыласуына әкеліп соқтырады. Сондықтан қызметкерді оқыту, жарнама, құжаттардың сапасы ж/е адамдардың тәртібі бұл жерді шешіледі рольойнайды. Кескінде(1сурет ) үзік сызықтармен маңызды роль атқаратын математикалық түсініктер берілген.
1. 1. 1-сурет. Кезеңдерді қабылдау шешімі
Операцияның мақсатын әр-түрлі түсінуге болады. Қандай да бір мақсатқа жету үшін технологиялық ұйымдастыру ж/е модельді жан-жақты зерттеу қажет. Қазіргі кезде күрделі есептердің шешілу жолдарына үлкен ұжымды қатыстырады, олар әр түрлі кәсіби дайындықтағы ж/е бағыттағы, адамдар, олар басқарушыдан зерттеуші маман ж/е қатардағы орындаушыға дейін есеп туралы түрлі деңгейде хабардар адамдар. Модельдеу барысындағы көптеген идеяларды қолдану нақты математикалық мәдениетті талап ететін қарапайым түсініктеме бере алады, модельді қолдану кезіндегі аппарат өте қарапайым да көріктіболу қажет. Модельдеу әдістері математика тілінде берілген есептерді шешуге қабілетті. Ал бұл қиын жағдайларды жеңілдетуге тура келтіреді.
1. 2 Модельді классификациялау
Ғылыми ж/е практикалық есептерді шешуге әр түрлі модельдеу құралдары қолданылады. Физикалық модельдеу - зерттеліп отырған нысанның физикалық табиғатты сақтай отырып физикалық құбылысының ұқсастығын пайдалана зерттелетін нысан. Геометриялық бірлестігі мен, модель н/е зерттелетін нысанның тиісті параметрлік масштабын сақтай отыру кезекті шарттары болып табылады. Зерттелген нысанға ұқсас критерші түрлері жетілдірілді, олар: электрлі, гидравликалы, аэро динамикалы ж/е т. б. Теориялық (математикалық) моделдеу шарттылық матиматикалы суреттеп, зерттеліп отырған нысанды елестету арқылы зерттеудің әдісі. 60-жылдың басында аралық дәрежедегі орын алатын физикалық ж/е математикалық модельдеуде квазианологта моделдеу әдісі жетілдірілді. Бұл әдіс зерттеліп отырған нысанды экспериментальды зерттеу емес. Математикалық ұқсас эквивалентті нәтиже алатын басқа физикалық табиғаты бар нысан (1. 1. 2-кесте) .
1. 1. 2-кесте. Квазианалогты модельдеу әдісінен мысал
М-масса
Х-ауыспалылық
V-жылдамдық
Q=
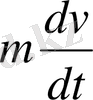 -күш
-күш
S=
 -Коэффицент шапшанды қажалу
-Коэффицент шапшанды қажалу
L-Индукция
q-Қуат
І-Ток
Е=
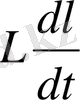 -ЭДС
-ЭДС
R=
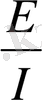 -Кедергі
-Кедергі
С-Сыйымдылық
ψ-потокосцепление
U-күштену
І=
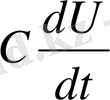 -Ток
-Ток
γ=
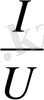 -Өткізгіштік
-Өткізгіштік
Математикалық модельді жетілдіріп, қолдану үшін математиканы жақсы білу қажет. Математикалық модельдеудің мәртебесі оның онай кеңеюі мен әртүрлі обылыстарда қолданылуы. Физикалық модельдеудің басты кемшілігі жоғары бағасы мен жан-жақты емес екендігі. Квазионолокты модельдердің негізгі мәртебесі оның төмен бағасында ж/е экспериментті тиімді уақыт масштабында бақылау, ол негізгі кемшілігі - модельдің жоғары салыстырмалы қателігінде. Бұл мінездемелер физикалық модельдердің қай облыстарда қолданатынын анықтайды. Мысалы: шағынаудан салатын модель, инвесторларды тарту арқылы өтетін көліктер тасқынын зерттеу үшін берілген модель барлық жағдайларда сыналған математикалық модель.
Берілген курста біз тек қана математикалық модельді оқитын боламыз. Белгілі бір шешімдерді қабылдауды талап ететін математикалық модельдерді суреттейтін түрлі жағдайлар бар. Олардың ішінен келесі 3 класты бөліп айтуға болады, олар детерминизерлерген, стохастикалық ж/е ойын модельі.
Жағдайға сәйкес негізгі факторлар анықталып белгілі болуы детерминарленген модельді жетілдіруден шығады. Пішімді шешім критериясы кейбір аптималды шаманың міндеті.
Стохастикалық модельдер кейбір анықталмаған, кездей соқ факторларда қолданылады. Қарсыластар мен одақтастардың қызығушылығы бірдей болса теориясы ойын модульі қолданылады.
Стохастикалы ж/е атын моделі жағдайда тиімді бағалау қосымша қиындықтарға әкеледі.
Бір жағынан критериді таңдау нақты жағдайларға байланысты, ж/е әртүрлі критериялардың тиімді шешім қабылдау мүмкін. Алдағы уақытта модельдердің статикалы, динамикалы, дискретті, үзіліссіз түрлері бола тұра біз модельдер классификациясына сүйенеміз.
Модельдер мен нысанның ұқсастық денгейі, изоторфизм мен галоморфизм түсінігінде айқындалады. Модель мен нысанның арасындағы сәйкестіктен изоморф модель нысанын құруға болады, сондай ақ модель элименттері мен нысан элименттерінің арасындағы сипаттамаларының ұқсастығы . Негізгі құрылымның кескінінің ұқсастығы галоморфизм түсінігін береді. Жеңілдетілген ж/е дерексіз құбылыстардың нәтижесі гамоморфті модель болады.
Изоморфты модельдерден көрі гамоморфты модельдер көбірек.
Егер керекті кіріс параметірлерінің шешімі берілсе, онда модель әрі тиімді шешімге баға береді. Кейде мұндай модель функциясы тура есептер шешімдері болып аталады.
Максималды шешімге қол жеткізе отырып берілген параметрлар біршама белгісіз шешімді табу көбінесе кері есепті шешуде талап етіледі.
Математикалық бағдарлама жасау әдісінде кері есептерді шешетін құрал кеңінен пайдаланылады.
Қазіргі математикалық бағдарламада түрлі есептер шешіміне байланысты, бірнеше бөлімдерге бөлінеді. Олар: желілік, желілік емес, дискретті, динамикалы, геометриялы, стохастикалы бағдарлау. Кейбіреуі жұмыс оқулығында қарастырылады.
Модельдерді жетілдірумен жорыққа шығаруда оның нақты ж/е қарапайым шын балансын табу қажет. Әрекеттегі модельдердің құрылымдармен байланыстырылуы тәжірибе мен жаттығу барысында болады ж/е нақты жағдайларда математикалық суреттеулермен сәйкестін процесінде кездеседі. Әрине бірде бір математикалық модель зерттеліп отырған мәселенің ерекшеліктерін қамти алмайды. Сондықтан операцианың нәтижелі жүрудегі процесі матиматикалық модельді құру үшін берілетін мақсаты болып қолаберетін ғылым ғана емес сонымен қатар өнер болып саналады.
1. 3 Сызықты программалау есептері (СПЕ) модельдерінің түрлері және құру жолдары
Сызықты теңсіздіктер және олардың СПЕ орны
Экономикалық, техникалық және басқа жоспарлау есептерін құруда теңсіздіктердің маңызы зор. Алгебралық теңсіздіктердің көмегімен көптеген есептердің шарттарын математика тілінде жазуға болады.
Алгебралық теңсіздіктердің тәжірибелік сызықты программалау есептерінде қолдану негізін түсіну үшін біраз қарапайым мысалдар қарастырайық.
1-есеп. Менеджер тігін фабрикасына екі түрлі матадан екі үлгіден киім тігу жұмысының ұтымды жоспарын құруы керек. Әрбір үлгіде тігілетін киімге матаның екі түрі пайдаланылатын болсын. Әрбір үлгіден бір киім тігуге төменгі кестеде көрсетілгендей әр мата метрі қажет делік.
Бұл көрсеткіштерді экономика ілінде нормативтік коэффициенттер деп атайды.
1. 3. 1- кесте. Мысал
1 үлгідегі
2 үлгідегі
0, 6
0, 8
1, 2
0, 6
Тігін орнында матаның бірінші түрінен 24 метр, екінші түрінен 36 метр болсын. Ал бірінші үлгі бойынша тігілген киімнің бағасы 16 мың теңге, екінші үлгімен тігілген киімнің бағасы 12 мың теңге болса, қолдағы бар матадан қандай үлгіден қанша тігілгенде ең көп табыс келтіретін жоспар жасау қажет.
Есепті шешу үшін бірінші үлгіден жасалатын киімнің бізге белгісіз саны Х, ал екінші киімнің санын Х деп алайық. Бұл белгілеу бойынша тігілген киімдерден түсетін жалпы табысты былай өрнектеуге болады:
Z = 16X 1 + 12X 2 → max
Мұндағы 16Х 1 - бірінші үлгідегі киімнен түсетін табыс. 12Х 2 екінші үлгілегі киімнен түсетін табыс, ал Z екі үлгідегі киімнен түсетін жалпы табысты көрсетеді. Есептің шарты бойынша Z ең көп табыс болу керек, сондықтан ең көп (ең үлкен) дегенді максимум немесе қысқаша математика тілінде MAX деп белгілеуге болады.
Енді есептің шарттарын жазайық. Бірінші матадан бірінші үлгідегі киімнің бір данасына 0, 6м керек болса, Х данасына 0, 6Х 1 қажет болар еді, ал осы матадан екінші үлгідегі бір дана киімді жасау үшін 0, 8 м керек болса, Х данасына 0, 8Х 2 қажет. Екі үлгідегі киімге жұмсалатын матаның қолда бары 24 м - ден артпауы керек. Ендеше бірінші мата үшін мына теңсіздік орындалады:
0, 6Х 1 + 0, 8Х 2 ≤ 24
Сол сияқты теңсіздікті екінші мата үшін жазайық:
1, 2Х 1 + 0, 6Х 2 ≤ 36
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz