Жекелеген атомдардың энергия спектрларының ерекшеліктері

Пән: Электротехника
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

Мазмұны:

Кіріспе2
Жекелеген атомдардың энергия

спектрларының ерекшеліктері3-8

Бор постулаттары

Шредингер теңдеуін шешу үшін

қолданылатын жуықтаулар8-11

Электрондардың толқындық қасиеттері12

Луи де Бройль толқындары12-14
Толқындық функция және оның физикалық мағынасы14-15

Шала өткізгішті диодтар15-18
Ганн генераторының жұмыс істеу принципі18-22

Ганн диодтарындағы СВЧ шайқалуының генерациясы22-24

Қолданылған әдебиеттер25

Кіріспе.

Қазіргі кезде біз технология аса дамыған, бұрынғы кездері механикалық түрде жасайтын жұмыстарды автоматты түрге айналдырған заманда өмір сүреміз. Мысалға: автокөліктер, мен ғимараттардың сигнализациясы, автоматты түрде ашылатын есіктер, кондиционерлер, әр түрлі детекторлар және т. б.

Жартылай өткізгіштер, ерекше зат түрінде, XIXғ аяғынан-ақ белгілі, тек қатты дене теориясының дамуы ғана олардың ерекшеліктерін анықтауға мүмкіндік береді. Бұдан көп уақыт бұрын: фотоөткізгіштік металл-жартылай өткізгіштердің байланысындағы тоқтың түзелу эффектісі анықталған.

Бастапқы мәнінен жоғары болатын тұрақты электр өрістің кернеулігін, n типті GaAs біртекті түрдегі СВЧ-тербелісінің генерациясының ең бірінші болып 1963 жылы Дж. Ганн бақылады (сондықтан да мұндай приборларды Ганн диодтары деп атайды) . Ганн генераторы арқылы электромагниттік толқындардағы зарядтарды тасушы ретінде біз күнделікті өмірде істелінетін жұмыстарды автоматты түрде ауыстыруға болатынына, жұмыс пен уақытты көп үнемдеуге болатынына көз жеткіздік.

Оқшауланған атомның энергия спектрі. Сутегі тәріздес атомдар үшін Бор ілімі. Бор постулаттары

XIX ғасырдың II-ші жартысынан бастап, сәуле спектрлеріне көптеген егжей-тегжейлі зерттеулер жүргізілді. Молекулалардың, атомдардың сәуле шығару спектрі жеке-жеке сызықтардан тұратындығы анықталды. Осыған байланысты атомдық спектрлер сызықтық деп аталады. Әрбір элементтің тек өзіне тән сызықтық спектрі болады және оның құрылысы атомды қоздыру амалына тәуелді болмайды. Сондықтан, спектрі бойынша оны шығаратын элементті анықтауға болады.

Атомдардың оптикалық спектрлерінде байқалатын заңдылықтарды түсінуде 1913 жылы Н. Бордың (1885-1962) ұсынған постулаттарының орны ерекше. Планк пен Эйнштейн (1879-1955) ұсынған кванттық түсініктерді дамытьш, Н. Бор энергияның дискреттілігі жөніндегі ұғымды атомға қолданды. Ол сол кез үшін өте батыл, классикалық түсінікке қайшы келетін постулаттар ұсынды. Осы постулаттар негізінде сутегі атомы спектрлеріндегі зандылықтарды түсіндіру мүмкін болды.

Атомдардың оптикалық спектрлерін түсіну үшін Бордың «электрондарға Планк пен Эйнштейннің кванттық шарттарына қанаттандыратын энергия қабықшалары ғана рұқсат етіледі» деген ғажайып жорамалының орны зор. Бұл қабықшаларды орнықты энергия қабықшалары дейді. Басқаша айтқанда, орныққан энергия қабықшалары атомдағы электрондардың рұқсат етілген күйлеріне сәйкес болады. Бордың жорамалы үш постулатқа әкелді.

1-постулат. Орнықты энергия қабықшаларындагы электрондары шеңбер бойымен айналмалы қозғалыста болса да, атомдар электромагниттік толқын - сәуле шыгармайды.

2-постулат. Орнықты энергия қабықшаның бойымен айналмалы қозғалыстағы электрондардың импульс моменттері квантталады, оның рұқсат етілген мәндері

Lm=meυr = ћn, n = 1, 2, 3 . . . (1)

теңдігімен анықталады.

Кванттық механика ілімінде Бордың 2-ші постулатын, басқаша былай тұжырымдайды: электрондардың энергия қабықшасы орнықты болу үшін, бойымен электрон козғалатын шеңбердің ұзын бойына толқын ұзындығыньң бүтін саны сыйю керек, яғни,

2πr=nλ, n =1, 2, 3…. (2)

теңдігі орындалу керек. Мүнда r - бойымен электрон козғалатын шеңбердің радиусы. Шындығында, электронның толкын ұзындығын

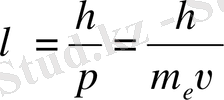(3)

Де-Бройль қатынасымен пайдалансак, (2) -тендігі

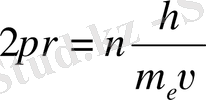(4)

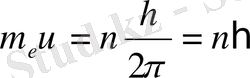не (5)

теңдіктеріне көшеді. (5) тендеуі Бордың (1) -қатынасымен дәл келеді.

Ал, Максвеллдің классикалық теориясы бойынша, электрондары айналмалы қозгғалыстағы кез келген атомдар сәуле шыгару керек, яғни Бордың бірінші постулаты классикалық физиканың тұжырымдарына қайшы келеді. Бұл қиыншылықтан Бор үшінші постулаты арқылы шықты.

3-постулат. Атом электромагниттік толқынды - сәулені тек бір орнықты куйден екінші орнықты күйге көшкенде ғана шығарады, не жұтады. Көшу негізінде шығатын сәуле энергиясы, жиілігі Эйнштейн - Планк

Wn-Wn=hv (6)

қатынасымен анықталады.

Бор постулаттарын пайдаланып, сутегі тәріздес атомдарындагы электрондардың орныққан энергия қабықшаларының радиустарын, энергияларын табайық.

Сутегі тәріздес атомды - бір электроны бар атомды қарастырайық. Атом ядросының заряды +Ze. Электрондар ядроны дөңгелек орбиталар бойынша айналсын. Электронның ядроға кулондық тартылу күші центрге тарту үдеуін υ2/r туғызады. Ньютонның екінші заңынан:

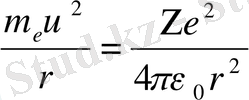
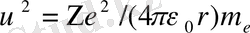
өрнектерін табамыз. (5) -қатынасымен анықталатын Бордың 1-постулатын және (8) -теңдігін пайдаланып,

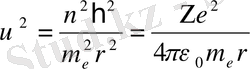(9)

өрнегін аламыз. (9) өрнегінен электронның рүқсат етілген орбиталарының радиусы

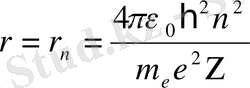, n=1, 2, 3 . . . (10)

теңдігімен анықталатын дискретті мәндер қабылдайтынын байқаймыз.

Енді осы күйлерге сәйкесті атом энергияларын есептейік. Сутегі тәріздес атомның энергиясы электронның Wk кинетикалык энергиясымен электрон мен ядроның әсерлесуінен туатын Wn потенциалдық энергиясының қосындысымен анықталады:

W = WK+Wn = 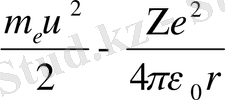Equation. 3 (11)

Шындығында, атомның электроны да, ядросы да массалар центрін айнала қозғалады. Бірақ тя » те болғандыктан, ядроның жылдамдығы электронның жылдамдығынан аз болады. (8) - өрнегін пайдаланып, (11) - өрнегінен

W = -Ze2/(8πεor) (12)

қатынасын аламыз. Бұған электрон орбитасының rn мәнін қойып, орнықты күйлердегі сутегі тәріздес атомның толық ішкі энергиясы үшін

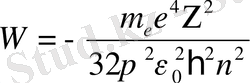Equation. 3, n= 1, 2 . . . (13)

өрнегін аламыз. Атомның орнықты күйінің энергиясын анықтайтын n кванттық саны бас кванттық сан деп аталады.

Оқшауланған сутегі атомындағы электрондардың, яғни, Z = l болғандағы, (13) орнегі бойынша табылған энергия спектрі 7. 4. 1-суретте берілген. Кез келген оқшауланған көп электронды атомдағы электрондардың энергия спектрі осы спектрге ұқсас болады.

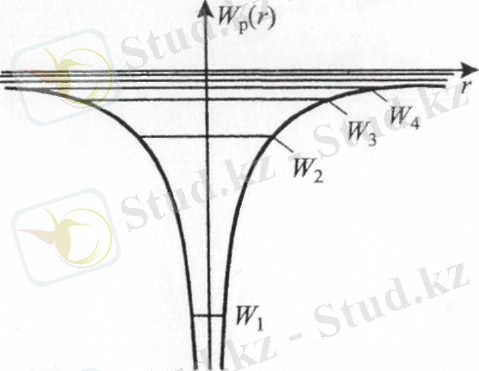
1-сур. Оқшауланған сутегі атомындағы электронның энергия спектрі

Суреттен сутегі атомындағы электронның энергия спектрі W < 0 болғанда дискретті, ал W > 0 болса, үздіксіз болатындығын және энергия өсіп нөлдік мәнге жақындаған сайын олардың арақашықтығының азаятындығын көреміз.

(12) -орнегінен, Z = l болганда, сутегі атомының электрондарының орнықты күйлерлеріне сәйкесті энергиялары алынады. Атомның электрондарының энергиясының ең аз мәнімен анықталатын күйі негізгі күй деп аталады. Қалған күйлер қозған күйлер болады. Сутегі атомының негізгі күйінің (n =1) энергиясы мынаған тең:

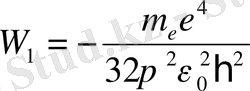= 13, 6 эВ.

Атомның негізгі күйіне сәйкесті электрон орбитасының радиусы былай анықталады:

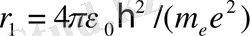Equation. 3 = 0, 053 нм. (15)

Бұл шама 1-Бор радиусы деп аталады.

Бордың 2-постулатын пайдаланып, сутегінің спектр сызықтарының мүмкін болатын жиіліктерін төмендегі өрнекті пайдаланып, табуға болады:

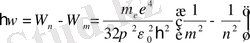(16)

Осы өрнектен, 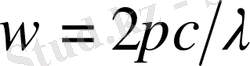екендігін ескеріп, мына өрнекті аламыз:

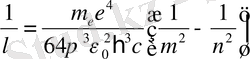(17)

Егер Ридберг тұрақтысы

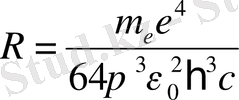(18)

қатынасымен анықталса, (18) -қатынасы Бальмердің жалпы өрнегімен дәл келеді.

(18) -қатынасымен mе, ћ, е, ε0, с шамаларының мәндерін

пайдаланып есептелінген Ридберг түрақтысының сандық мәні спектроскопиялық өлшеулерден алынған деректермен жақсы үйлеседі. Сонымен, Бор теориясы сутегі және сутегі тәріздес иондардың сәуле шығару спектрін жақсы түсіндіреді.

Атомдар энергиясының дискреттігі олар жарық шығарғанда, не жұтқанда ғана емес, басқа да көптеген жағдайларда да байқалады. Мәселен, Франк-Герц тәжірибелерінде атом энергиясының дискреттігі атомдар электрондармен соғылысқан жағдайда байқалады.

Осылардың бәрі атом энергиясы дискретті болады деген Бор ұйғарымын растайды. Бірақ кейіннен түзету енгізіліп, жетілдірілгенімен Бор теориясы микробөлшектерге байланысты көптеген құбылыстарды түсіндіре алмады. Мөселен, Бор постулаттары негізінде екі электроны бар атом-гелий атомының теориясын құру мүмкін болмады. Бүған қоса Бор теориясы логикалық қарама-қайшылықсыз емес еді: бір жағынан, энергия мен импульс моменті дискретті өзгереді деп кванттық түсініктерді қолданды, ал, екінші жағынан, электрон жөнінде классикалық түсініктерге суйенді.

Көптеген атомдық құбылыстарды түсіндіруге Бор теориясының жарамауы оның жеткілікті дәрежеде дамымағандығынан емес, оның принциптік кемістігіне байланысты еді. Бүл теорияның электрон жайындағы қате түсінікке негізделгені анық. Классикалық теорияда электрон дискретті бөлшек деп қарастырылады. Ал XX ғасырдың 20-жылдары алынған деректер электронның

әрі толқындық, әрі корпускулалық қасиеттері болатындығын дәлелдеді.

Қорытынды:

- атомдагы электрондар энергия бойынша рұқсат етілген орнықты қабықшаларының бойымен қозғалады;

- Бордың постулаттары:

а) орнықты энергия қабықшаларының бойымен айнал-
малы қозғалыстағы электрондар электромагниттік
толқын - сәуле шығармайды;

б) орнықты энергия қабықшаларының бойымен айналмалы
қозғалыстағы электрондардың импульс моменттері
квантталады;

в) атом электромагниттік толқынды - сәулені тек бір
орныққан күйден екінші орныққан күйге көшкенде ғана
шыгарады, не жұтады.

- оқшауланған атомдардағы электрондардың энергия спектрі дискретті, квантталады.

Шредингер теңдеулері

Де Бройль зерттеулері микробөлшектердің қозғалысын сипаттайтын жаңа механиканың негізін салуға көмектесті. 1925-1926 жж. неміс ғалымы В. Гейзенберг пен австриялық Э. Шредингер өз беттерінше жаңа механиканың екі вариантын ұсынды. Бұл екі варианттың нәтижесі бірдей, бірақ есептеуге қолайлы болғандықтан Шредингер теңдеуі жиірек қолданылады.

Атом мен молекула құрылыстарының қазіргі теориялары да осы әдіске сүйенеді. Бұл теориялар микробөлшектердің қозғалысын және күйін сипаттайтын болғандықтан квант механикасы деп атала бастады. Ал Ньютон заңдарына негізделген макроденелерге арналған механика-классикалық механика делінеді.

Бор-Зоммерфельд теориясы классикалық және кванттық көзқарастың басын жасанды түрде біріктірсе, квант механикасы ешбір қайшылықтары жоқ ұғымдарға негізделген бүтіндей теория. Бұл теория бойынша есептеліп алынатын нәтижелер эксперимент жүзінде толығымен дәлелденіп отыр.

Квант механикасында микробөлшектердің қозғалу заңдарын Шредингер теңдеуі сипаттайды. Шредингер теңдеуі оптикадағы толқындарға арналған теңдеу мен (сондықтан толқындық теңдеу деп те аталады) де Бройльдің теңдеуін бірге пайдаланып шығарылған. Сондықтан бұл теңдеу микросистеманың күйін ондағы микробөлшектердің екі жақты табиғатын ескере отырып сипаттайды.

Де Бройльдің теңдеуі дәлелдеуді керек етпейтін постулат, олай болса, Шредингер теңдеуі де постулат. Бірақ оның нәтижелері көптеген эксперименттермен дәлелденгендіктен квант механикасы табиғат заңы деп есептеледі. Ол материалды дүниенің заңдылықтарын механика тұрғысынан объективті бейнелейді. Сондықтан Ньютон заңдары классикалық механикада қандай роль атқарса, Шредингер теңдеуі де квант механикасында сондай бағаланады.

Шредингер теңдеуі дербес туындылары бар дифференциалды теңдеу түрінде өрнектеледі.

Кванттық механиканың негізгі теңдеуі болып толқындық функцияға арналған Шредингердің 1926 ж. ашқан ұсақ, бөлшектер күйін сипаттайтын теңдеуі жатады. Бұл теңдеу бұрыннан белгілі қатыстардан қорытылып шығарылмай, тек көптеген ғылыми тәжірибелердің нәтижелерінен табылады. Сонымен Шредингер теңдеуінің жалпы түрі мынадай

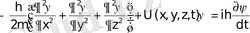Equation. 3 (1. 10)

мұндағы Equation. 3 = h/(2π) = 1, 05·10-34 Дж. с, m - бөлшектің массасы, U(x, y, z, t) -күштер өрісіндегі бөлшектің потенциалдық энергиясы, i - жорымал сан, 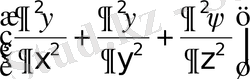Equation. 3 - бөлшектің кеңістіктегі координаты.

(1. 10) теңдеудегі ψ функциясы потенциалдық өрістегі бөлшекке әсер ететін күштердің потенциалдық энергиясы арқылы анықталады. Сөйтіп U потенциалдық энергия уақыт пен координат функциясы екендігін байқаймыз, яғни

ψ(х, у, z, t) = е -і (Е/ħ) t ψ(х, у, z), (1. 11)

мұндағы Е - бөлшектің толық энергиясы.

Егер (1. 11) өрнекке (1. 10) теңдеудегі функция мәндерін қойып және бірнеше түрлендірулерден кейін функцияның мына түрдегі дифференциалдық теңдеуін аламыз:

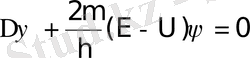Equation. 3 (1. 12)

Осы теңдеу Шредингердің бөлшектің стационарлық күйін сипаттайтын теңдеуі деп аталады. (1. 12) теңдеудегі Δ - Лаплас операторы деп аталады да, ол мынаған тең Δ=∂/∂х2+∂/∂y2 + ∂/∂z 2.

Мұнда координаттардың декарт системасының басын атом ядросымен сай келтіріп алып, сол ядро өрісінде электрон бола алатын кез келген М нүктесінің координаттарын х, у, z деп алған (1. 3-сурет) . Жоғарыдағы теңдеудегі бізге белгісіз шамалар: U-берілген нүктедегі электронның потенциялдық энергиясы. Оның мөлшері сол нүктенің ядродан қашықтығына, әрі зарядының шамасына тәуелді. Е-электронның толық энергиясы.

Шредингер теңдеуіне кіретін айнымалы шама 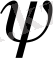(пси) - толқындық функция деп аталады. Оның квадратының ( 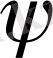) 2 физикалық дәл мәні бар: ол микробөлшектің кеңістіктің белгілі бір жеріндегі болу ықтималдығын сипаттайды. Егер оны атомдағы электронның жағдайына сай қарасақ, онда ( 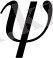) 2, электронның атомының кез келген нүктесіндегі болу ықтималдығының тығыздығын көрсетеді. Тығыздықты сол микробөлшектің берілген нүктедегі «өмір сұру» уақытының мөлшеріне қарай бағалауға болады. Мысалы, атомның бүкіл «өмірі» 1000 сек десек, соның М нүктесінде электрон 1 сек болатын болса, электронның осы нүктесіндегі болу ықтималдылығының тығыздығы 0, 001-ге тең.

Өзінің физикалық мәніне сай толқындық функция шекті, үздіксіз әрі бір мәнді болып, ал электрон жоқ жерде оның мәні нөлге айналуға тиіс. Мәселен, ондай жағдай электрон ядродан шексіз алыстағанда, яғни олар өзара байланысын түгелдей үзгенде болады.

Қазіргі атомдар теориясында Шредингер теңдеуінің шешуі дегеніміздің өзі жоғарыда келтіргендей қасиеті бар, теңдеуді қанағаттандыра алатын 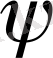функциялардың және оған сай энергия Е мәндерін табу болып табылады. Көптеген жағдайда Шредингер теңдеуінің математикалық анализ негізінде ядроның маңындағы кез келген нүктедегі электрон ықтималдылығының тығыздығын есептеп, оларды өзара салыстыруға болады.

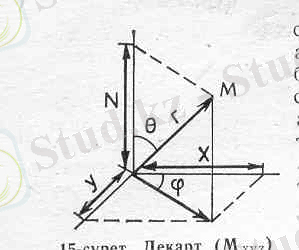
1. 3-сурет. Декарт (Мxyz) және полюсті ( 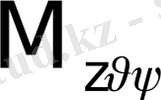Equation. 3 ) координаттар

системасындағы М-нүктесі

Сонымен біз еркін қозғалыстағы бөлшектерге арналған Шредингер теңдеуін алдық. Бұл өрнектегі толық энергия Е потенциалдық өрістегі қозғалып жүрген бөлшектердің кинетикалық Ек және потенциалдық энергиясының U қосындысы болып есептеледі.

Әрине, бұл пікірдің кванттық механикада шектеулік сипаттамасы болады.

Тағы да бір атап өтетін жай, ол бөлшектердің уақыттың берілген мезетіндегі күйін, бөлшектердің толық энергиясының циклді жиілігі бойынша ω=Етол/ħ сипаттау, де Бройль толқынына сәйкес кванттық мехаңиканың негізі болып табылады.

Егер функциясы бір жерде бір мәнді, шектеулі және үздіксіз болып, шексіз қашықтықта нөлге айналатын болсын десек, онда Шредингердің теңдеуін бөлшектің толық энергиясының кез келген мәндерінде шешуге болмайды, тек оның кейбір мәндері үшін ғана шешуге болады. Олай болса, энергияның осындай мәндері Шредингер теңдеуінің меншікті мәндері деп аталады. Ал оларға сәйкес толқындық функциялар қарастырылып отырған есептің меншікті функциялары болады. Олар атомның стационар күйлерін сипаттайды.

Сөйтіп атомдық спектрлерді зерттеп келгенде байқалған атом энергиясының дискрет мәндері толқындық теңдеудің меншікті мәндері болып табылады. Шредингер теңдеуін толық шешіп тек теңдеудің меншікті мәндерін ғана емес, есептің де меншікті функцияларын да табуға болады.

Электрондардың толқындық қасиеттері

Кванттық механика - микробөлшектердің - молекулалардың, атомдардың козғалыстары мен әрекеттесулерін зерттейді.

Кванттық теория бойынша электрон әрі материалдық бөлшектің, әрі толқынның қасиеттерін көрсетеді.

Оның материалдық бөлшек сияқты белгілі массасы болады, қысым туғызады, сонымен бірге электрондар қозғалғанда толқындық құбылыстар байқалады.

Толқындық қасиеттері бар электрон өте шапшаң қозғалып ядро төңірегіндегі кеңістіктің кез келген бөлігінде бола алады. Сондықтан қазіргі көзқарас бойынша электрон ядро төңірегінде белгілі тығыздығы бар теріс зарядтардың электрон бүлтын түзеді.

Электрон бұлтының мөлшерін, пішінін және кеңістіктегі орналасу бағытын көрсететін электронның күйін атомдық электрондық орбиталь дейді.

Де Бройль толқындары

Де Бройль 1924 жылы толқындық-бөлшектік дуализм фотонмен қатар басқа да барлық микробөлшектерге тән деген гипотеза айтты. Де Бройль гипотезасы бойынша кез келген қозғалыстағы бөлшек, мысалы, электрон толқындық қасиетке ие.

Мысалы, m бөлшек 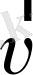Equation. 3 жылдамдықпен қозғалсын. Оның энергиясы Ε және импульсі 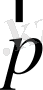Equation. 3 болсын. Біз энергия мен импульстің салыстырмалылық теориясындағы формулаларын білеміз: E = mc2, 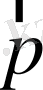Equation. 3 = m 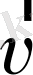Equation. 3 .

Жалпы жағдайда масса жылдамдыққа тәуелді:

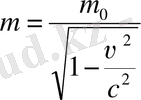
мұндағы m0 - тыныштық массасы.

Екінші жағынан алғанда, егер бөлшекке толқындық қасиеттер тән болса, ол ν жиілік пен λ толқын ұзындығы арқылы сипатталуы тиіс, яғни бөлшектің корпускулалық және толқындық қасиеттерінің арасында бірмәнді байланыс болуы керек. Де Бройль тыныштық массасы бар бөлшектер үшін де фотонды сипаттайтын қатынастарды жазуға болады деп есептеді:

Ε = ħω, 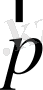= ħ 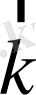, (7. 12)

мұндағы 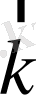- толқындық вектор, оның модулі 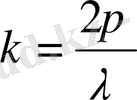. Олай болса,

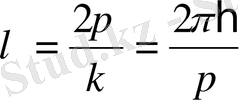немесе

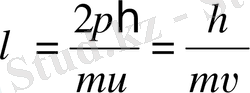. (7. 13)

Сонымен, импульсі p бөлшекке ұзындығы (7. 13) өрнегімен анықталатын толқын сәйкес келеді, оны Де Бройль толқыны деп атайды. Егер бөлшек баяу қозғалатын ( <<1) болса, (7. 13) формуласындағы m бөлшектің тыныштық массасына тең.

Қазіргі кезде микробөлшектердің толқындық қасиеттері жақсы зерттелген, кеңінен белгілі эксперименттік факт болып есептеледі. Мысалы, электрондардың дифракциясын кристаллдың құрылымын зерттеуге қолданады. Бірақ кезінде бөлшектердің толқындық қасиеттерін болжау, соңынан оны тәжірибелерде дәлелдеу - физикадағы ашылған ұлы жаңалық болды. Себебі, ол кезде бір нәрсенің бойында әрі толқындық, әрі бөлшектік қасиеттің қатар болуы мүмкін емес сияқты еді. Физиктер электронды барлық жағынан алғанда кәдімгі классикалық бөлшек деп санады.

Классикалық бөлшектің энергиясы мен импульсі бөлшектің өзі тұрған жерде шоғырланады, ол бірмәнді анықталған траекторияның бойымен қозғалады. Басқаша айтсақ, бөлшек деген үзікті, дискретті нәрсе.

Монохромат толқын уақыт бойынша да, кеңістікте де үздіксіз таралады. Алдымен жарықтың электромагниттік толқындық табиғаты зерттелді. Кейінірек жарықтың корпускулалық қасиеттері ашылды. Мұнан соң барып, фотондардың екіжақтылық, корпускулалық -толқындық қасиеттері зерттелді.

Қазіргі кезде тыныштық массасы бар атомдар, электрондар, протондар, нейтрондар сияқты бөлшектердің фотон тәрізді әрі бөлшектік, әрі толқындық қасиетке ие екені белгілі. Бұл оларға тән, олардың ішкі қасиеттері. Микробөлшектер дүниесіне классикалық физиканың заңдары жүрмейді. Бірақ кванттық теория классикалық теорияны жоққа шығармайды. Кванттық теорияның аясына классикалық теория да кіреді (сәйкестік принципі) .

Де Бройль толқындарының кеңістіктің қандай да бір жеріндегі интенсивтігі бөлшекті осы жерден табу ықтималдығына пропорционал. Де Бройль толқынын осылайша түсіндіру бөлшектің құрылымына қатысы жоқ, ол бүтін күйінде қалады.

Толқындық функция және оның физикалық мағынаы

ХХ ғасырдың басында ашылған бірқатар құбылыстар мен тәжірибелік айғақтар классикалық физиканың негізгі тұжырымдарымен қайшылыққа келіп, оларды зерделеу нәтижесінде жаңа, кванттық көзқарас дами бастады. Микробөлшектердің корпускулалық-бөлшектік қасиеттерінің анықталуы, атомдық физика саласындағы зерттеулер классикалық физика заңдарын микробөлшектерге қолдануға қойылатын шектеулерді айқындады. Мұның өзі микробөлшектердің қозғалыс және өзара әсерлесу заңдарын сипаттайтын кваттық механиканың туындап, дамуына себепкер болды.

Релятивтік емес (баяу бөлшектерге арналған) кванттық механиканың негізгі теңдеуін 1926 жылы Э. Шредингер тұжырымдап жазды.

Бұл - толқындық теңдеу және одан тәжірибелерде бақыланатын бөлшектердің толқындық қасиеттері шығады. Кванттық механикада бөлшектің күйін толқындық функциямен сипаттайды. Толқындық функция - координаталар мен уақыттың комплекстік функциясы, оның айқын түрі Шредингер теңдеуінің шешуінен шығады да, соңында бөлшекке әрекет ететін күштердің сипатымен анықталады.

Кеңістіктің берілген нүктесіндегі Де Бройль толқындарының интенсивтігі (амплитудасының квадраты) осы нүктеге түсетін бөлшектердің санын анықтайтыны туралы жоғарыда айтқанбыз. Ал, егер жеке бөлшек қарастырылса, оған сәйкес Де Бройль толқынының интенсивтігі бөлшектің осы нүктенің маңына түсу қтималдығын білдіреді. Кванттық механиканың ең маңызды ерекшелігі - микробөлшектің күйін ықтималдылық тұрғысынан сипаттау. 1926 жылы М. Борн ықтималдық амплитудасы деп аталатын шама толқындық заңдылықпен өзгереді деген болжам айтты, бұл шаманы толқындық функция немесе ψ (пси) - функциясы деп атайды.

Толқындық функцияның модулінің квадраты берілген уақыт мезетіндегі бөлшектің кеңістіктің элементар d V аумағында болу ықтималдығын анықтайды:

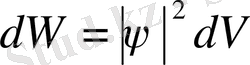Басқаша айтқанда, Де Бройль толқындарының интенсивтігі толқындық функция модулінің квадратымен анықталады. Егер кеңістіктің шексіз үлкен аумағын қарастырсақ, бөлшек міндетті түрде оның бір жерінде орналасуы керек, ал айқын оқиғаның ықтималдығы бірге тең. Олай болса, 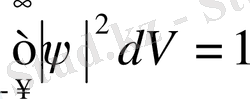Equation. 3

Соңғы өрнек толқындық функцияны нормалау шарты болып табылады.

Қорыта айтқанды, толқындық функция микробөлшек күйінің негізгі сипаттамасы бола отырып, оның күй параметрлерінің орташа мәндерін есептеуге мүмкіндік береді

Шала өткізгішті диодтар

Қазіргі кезде кремний, германий диодтары селен вентильдері кеңінен қолданылады. Жалпы шала өткізгішті диодтар нүктелік және жазық болып келеді.

Жазық диодтар электрондық-кемтік ауысуда үлкен ауданды қамтиды, сондықтан олар күшті тоқты түзете алады. Сумен суытылатын диодтар да болады, олар бірнеше жүз ампер токты түзете алады.

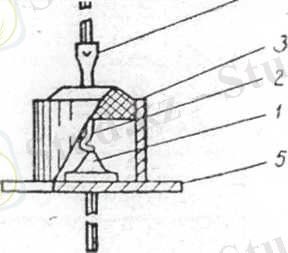
56-суретте жазық диодтың құрылысы көрсетілген. Онда металл корпус ішінде электронды өткізгішті германий кристалы бар. Оған индий балқытылып құйылған, ол германийге кірігіп, шала өткізгіштің кемтіктік типінің аймағын жасайды.