Реал жүйелердің күй теңдеулері және инертті газдардың Ван-дер-Ваальс параметрлерінің масштабтық талдауы


Реал жүйелердің құрылысы және күй теңдеуі
Біз мектепте көбіне идеал жүйелердің заңдылықтарын оқимыз. Ең алдымен идеал газдың заңдылықтарын еске түсірейік. Идеал газ деп молекулаларының арасында алыстан әсерлесу потенциалы жоқ, әсерлесу тек молекулалар өз-ара соқтығысу кезінде ғана болатын газды айтады. Егер біз осындай газдың күй теңдеуін білсек, ол теңдеуден газда болатын процесстердің, және басқада заңдылықтарын шығарып алуға болады.
Идеал газдың күй теңдеуін ғылымда Клапейрон -Менделеев теңдеуі деп атайды. Массасы m-ге тең газ үшін бұл теңдеуді былай жазады:
PV= (m/м) RT (1)
Мұндағы Р-газ қысымы, V-көлемі, Т-температурасы, м-газдың бір молінің массасы,
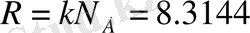 Дж/(моль. К) -универсал газ тұрақтысы - Больцман тұрақтысымен Авогадро санының көбейтіндісінен тұрады. Соңғы келтірілген k, N
Дж/(моль. К) -универсал газ тұрақтысы - Больцман тұрақтысымен Авогадро санының көбейтіндісінен тұрады. Соңғы келтірілген k, N
 -шамалары да барлық газдар үшін тұрақты болғандықтан R-ді универсал тұрақты деп атайды. Егер де біз газдың тек бір молін ғана қарастырсақ, онда Клапейрон-Менделеев теңдеуін мына түрде жазамыз:
-шамалары да барлық газдар үшін тұрақты болғандықтан R-ді универсал тұрақты деп атайды. Егер де біз газдың тек бір молін ғана қарастырсақ, онда Клапейрон-Менделеев теңдеуін мына түрде жазамыз:
PV=RT, (2)
Өйткені m=м.
Енді мысал үшін газда болатын кейбір процесстерді сипаттайтын теңдеулерді осы (1) немесе (2) теңдеулерден шығарып көрейік.
1. Изобаралық процесс газ қысымы тұрақты болған жағдайда жүреді:
P= Const, онда (2) теңдіктен осы процесстің теңдеуін аламыз:
V/T= Const. Мұны Гей -Люссак заңы деп атайды.
2. Изохоралық процесс газ көлемі тұрақты болған жағдайда жүреді.
V= Const, онда (2) теңдіктен оның теңдеуін аламыз:
Р/T= Const . Мұны Шарль заңы деп атайды.
3. Изотермалық процесс газ температурасы тұрақты болған жағдайда жүреді:
T= Const, онда (2) теңдіктен оның теңдеуін аламыз:
Р/V= Const. Мұны Бойль -Мариотт заңы деп атайды.
Дәл осы тәрізді басқа да кез-келген политроптық процесстердің де теңдеулерін осы (2) теңдікпен термодинамиканың 1 - бастамасына сүйеніп табу қиын емес. Идеал газда болатын басқа да түрлі құбылыстардың сипаттамаларын түсіндіргенде күй теңдеулерінің ролі өте үлкен.
Ал, табиғатта бар реал жүйелердің қасиеттерін зерттеуде де олардың күй теңдеулерін тауып, оларды пайдаланудың ролі аса зор екенін айрықша айтқан жөн. Ол теңдеулерді алудың жолы тек статистикалық микроскоптық теорияда жатыр. Бірақ оларды табу статистикалық физикада да өте күрделі мәселе. Оның ең басты қиындығы дене молекулаларының арасындағы әсерлесудің аналитикалық түрін табудың күрделілігінде жатыр. Осы уақытқа дейін реал денелердің күй теңдеулерінің аналитикалық түрі әлі жазылған емес. Бірақ бұл физиканың актуальді мәселесінің бірі. Әр зат үшін, көптеген жағдайда, күй теңдеулерін таблица түрінде қолданып келеді. Ол теңдеулерді физикада, техникада, химияда, астрономияда, энергетикада, т. б. да кеңінен қолданады.
Ал, күй теңдеуі молекулалардың арасындағы әсерлесу потенциалымен тығыз байланысты. Сондықтан молекулалардың әр сорты өз күй теңдеуін береді. Молекулалары әсерлесетін газдар мен сұйықтар үшін универсал теңдеу жоқ.
Молекулалардың ара қашықтығы өте аз болған жағдайда олардың арасында тебісу күші бар. Өйткені әр молекула өзі алып жатқан көлемге басқа молекулаларды жібермеуге тырысады. Ал екі молекула осы қашықтықтан алыстай бастаса олардың арасындағы әсерлесу тартылыс күшіне ауыса бастайды. Бірақ ара қашықтық молекуланың 2
 3 радиусындай жерге жеткенде тартылыс күші әлсіреп аяғында жоққа айналады. Байланыс потенциалының молекула арақашықтығына байланысы мына 1- суретте берілген.
3 радиусындай жерге жеткенде тартылыс күші әлсіреп аяғында жоққа айналады. Байланыс потенциалының молекула арақашықтығына байланысы мына 1- суретте берілген.
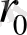
Егер
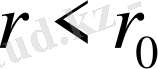 болса, молекулалар арасында - тебісу күші, ал
болса, молекулалар арасында - тебісу күші, ал
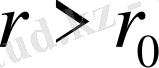 болғанда тартылу күші әсер етеді. Дәлірек айтқанда, бұл әсерлесу әр молекула түрі үшін түрліше болады. Сондықтан практикада қолданылатын эмпирикалық потенциалдардың түрлері көп. Солардың ішінде ең көп қолданылатыны Леонард -Джонс потенциалы мен Ван-дер -Ваальс потенциалы болып табылады. Бұл потенциалды жазғанда молекулалар арасында тек екі бөлшектік қана әсерлесу бар деп есептейді. Шындығын алғанда олардың арасында көп бөлшекті әсерлесу де бар. Әсіресе сұйықтар молекулаларында бұл әсерлесу үлкен роль атқаруы мүмкін. Ал потенциалдардың тартылыс күшіне сәйкес келетін бөлігі молекула ара қашықтықтарының алтыншы дәрежесіне кері пропорционал кемиді:
болғанда тартылу күші әсер етеді. Дәлірек айтқанда, бұл әсерлесу әр молекула түрі үшін түрліше болады. Сондықтан практикада қолданылатын эмпирикалық потенциалдардың түрлері көп. Солардың ішінде ең көп қолданылатыны Леонард -Джонс потенциалы мен Ван-дер -Ваальс потенциалы болып табылады. Бұл потенциалды жазғанда молекулалар арасында тек екі бөлшектік қана әсерлесу бар деп есептейді. Шындығын алғанда олардың арасында көп бөлшекті әсерлесу де бар. Әсіресе сұйықтар молекулаларында бұл әсерлесу үлкен роль атқаруы мүмкін. Ал потенциалдардың тартылыс күшіне сәйкес келетін бөлігі молекула ара қашықтықтарының алтыншы дәрежесіне кері пропорционал кемиді:
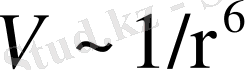 (3)
(3)
Яғни, потенциал молекулалар қашықтаған сайын тез әлсіреп жоқ болады. Сонымен бірге, тартылыс потенциалы - теріс таңбалы да, молекулалардың кинетикалық энергиясы - оң таңбалы. Егер берілген молекулалар жүйесі үшін кинетикалық және потенциалдық энергиялардың қосындысы оң мәнді болса, онда газ молекулалары үлкен қашықтыққа тарап кетеді, яғни, газ өз бетінше ұлғайып кетеді. Ал сұйық молекулаларының кинетикалық энергиясы онша үлкен емес. Сондықтан сұйықтағы кинетикалық және потенциал энергияларының барлық молекулалар бойынша қосындысы теріс мәнді. Олай болса сұйық көлемі өз бетімен ұлғая алмайды.
Реал жүйелердің күй теңдеуін жазу үшін, дегенмен, молекулалар арасындағы осы әсерлесуді еске алғанда, оларды мына вириалды теңдеу түрінде жаза аламыз, яғни оны Клапейрон -Менделеев теңдеуі түрінде, көлем бойынша қатарға жіктейміз:
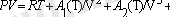 (4)
(4)
Бұл жердегі
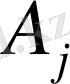 (T) вириал коэффиценттер. Әрине, мұндай шексіз қатардың вириал коэффиценттерін табу өте қиын мәселе. Іс жүзінде бұдан шығатын жуық теңдеуді пайдалануға болады. Солардың ішіндегі ең қарапайымы, ықшамдысы - газдың негізгі физикалық қасиеттерін есепке алатын көрнекті теңдеу ол Ван-дер-Ваальс теңдеуі. Соңғы теңдеуде вириал қатарының (4) оң жағындағы екінші мүшені ғана, яғни вириал коэффицентті анық түрінде былайша жазамыз:
(T) вириал коэффиценттер. Әрине, мұндай шексіз қатардың вириал коэффиценттерін табу өте қиын мәселе. Іс жүзінде бұдан шығатын жуық теңдеуді пайдалануға болады. Солардың ішіндегі ең қарапайымы, ықшамдысы - газдың негізгі физикалық қасиеттерін есепке алатын көрнекті теңдеу ол Ван-дер-Ваальс теңдеуі. Соңғы теңдеуде вириал қатарының (4) оң жағындағы екінші мүшені ғана, яғни вириал коэффицентті анық түрінде былайша жазамыз:
PV=RT+(RT b-a) /V (5)
Сонда көлемнің квадратына кері мүшеден басталатын барлық қосымшаларды алып тастаймыз.
Сөйтіп, реал газдар үшін теңдеуді оңайлатып (5) түріне келтірудің мынандай негізі бар. Молекулалардың бір бірімен тебісуі олардың белгілі бір көлемі бар екенін білдіреді. Молекулалардың әсерлесетін көлемдерінің қосындысын b-параметрі арқылы өрнектейміз. Ал екінші а-параметрі молекулалардың өз ара тартылыс әсерлесуінен туатын ішкі қысымның аздап азаятынын көрсетеді. Газ қысымын өлшейтін қондырғының қалақшасына келіп соғатын молекулалар импульсін молекулалардың өз ара тартылыс күші аздап азайтады. Осы әсерлесу (5) формуласында «а» параметрі өрнектеп тұр.
Кейінгі кезде осы теңдеудің қолданылу ауданы әлде қайда кең екені белгілі болып отыр. Бұрын оны тек бір атомды молекулалар қасиетін зерттеуге және олардан құралған жүйелердің сұйық және газ түріндегі агрегат күйлерінің ауысу процесстеріне ғана қолданып келген. Бұл жұмыстағы біздің негізгі мақсатымыз осы тендеуді екі атомды молекулалардан құралған газдардың тығыз және конденсацияланған күйлерінің физикалық барлық қасиеттерін табуға, түсіндіруге қолдану.
Әсіресе ол теңдеуді инертті газдардың барлық термодинамикалық параметрлерін табуға пайдаланамыз. Инертті газдарды толық сипаттайтын барлық термодинамикалық шамалар атомның екі бөлшектік әсерлесуінің екі параметрі арқылы өрнектеледі. Ол екі параметр 1 - суретте берілген әсерлесудің радиусы
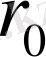 мен потенциалдың тереңдігі W. Бұл параметрлер әлем лабороторияларында түрлі әдіспен табылған
мен потенциалдың тереңдігі W. Бұл параметрлер әлем лабороторияларында түрлі әдіспен табылған
 , олардың орташа мәндері 1- кестеде берілген. Сонымен бірге сол таблица инертті газдардың 1 моліне сәйкес келтірілген параметрлері
, олардың орташа мәндері 1- кестеде берілген. Сонымен бірге сол таблица инертті газдардың 1 моліне сәйкес келтірілген параметрлері
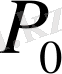 мен
мен
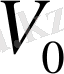 берілген.
берілген.
1 Кесте. Инертті газдар үшін екі бөлшектің әсерлесу потенциалының параметрлері мен келтірілген параметрлері.
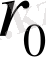 , А
, А
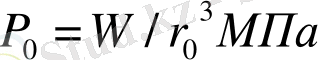
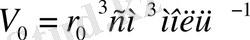
 мен W шамаларының көмегімен неон Ne, аргон Ar, криптон Kr, ксенон Xe инертті газдардағы екі атомның өз ара әсерлесу параметрлеріне сәйкес келетін Ван-дер-Ваальс теңдеуіндегі параметрлер «а» мен «b» табылған. Олар 2 - кестеде берілген. Осы кестеде сондай ақ осы параметрлердің келтірілген мәндері a/W
мен W шамаларының көмегімен неон Ne, аргон Ar, криптон Kr, ксенон Xe инертті газдардағы екі атомның өз ара әсерлесу параметрлеріне сәйкес келетін Ван-дер-Ваальс теңдеуіндегі параметрлер «а» мен «b» табылған. Олар 2 - кестеде берілген. Осы кестеде сондай ақ осы параметрлердің келтірілген мәндері a/W
 , b/
, b/
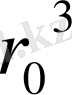 берілген.
берілген.
2 Кесте. Инертті газдар үшін Ван-дер-Ваальс теңдеуінің параметрлері мен олардың келтірілген мәндері.
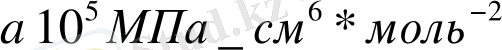

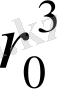
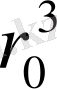
Соңғы кестеден біз Ван-дер-Ваальс теңдеуіндегі параметрлердің келтірілген мәндері, яғни олардың өздеріне сәйкес келетін потенциал параметрлеріне қатынасы барлық газдар үшін үлкен дәлдікпен бірдей деуге болады. Бұл тұжырымда жіберілетін қателік 1
 2 проценттен аспайды. Ол қателіктер тәжрибелерде
2 проценттен аспайды. Ол қателіктер тәжрибелерде
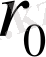 мен W параметрлерін анықтаудың дәлдіктерінен туатынына күмән жоқ.
мен W параметрлерін анықтаудың дәлдіктерінен туатынына күмән жоқ.
Сондай-ақ барлық инертті газдар үшін бірдей болып өз ара сәйкес келетін осы газдардың кризистік нүктесінің параметрлерін де табуға болады. Кризистік нүкте деп барлық газдарды сипаттайтын үш параметірдің T, V, P белгілі бір мәндерінде газдың сол жүйенің сұйық күйінен айырмашылығы толық жойылатын нүктені айтады. Сол нүктедегі осы үш параметрдің мәндерін былай
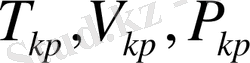 деп белгілейтін боламыз.
деп белгілейтін боламыз.
Қысымның, көлемнің және температураның осы кризистік мәндерінен бастап осы үш параметрдің жоғарғы мәндеріне дейін ол заттың сұйық пен газ агрегатты күйлерінің бір-бірінен еш бір айырмасы жоқ екені белгілі.
Математика тілімен айтқанда осы кризистік нүктеде температура тұрақты болғанда қысымның көлемге байланыстылығы жойылады. Олай болса мынандай шарттар орындалады:
(
д
P/
д
V)
 =0 және
=0 және
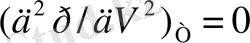 (6)
(6)
Осы теңдіктерді пайдаланып Ван-дер-Ваальс теңдеуі:
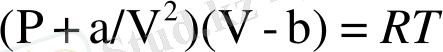 (7)
(7)
арқылы айтылған үш параметрдің кризистік нүктедегі мәндерін табамыз.
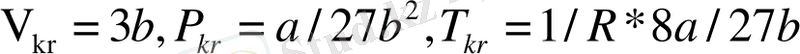 (8)
(8)
Газды сипаттайтын термодинамикалқ параметрлер Ван-дер-Ваальс теңдеулеріндегі екі молекулалық әсерлесуді сипаттайтын а мен b шамалары арқылы өрнектеледі. Олай болса қарастырып отырған макроскоп жүйенің кризистік нүктесі де молекулалардың макроскоптық әсерлесу арқылы анықталады екен. Ал, осы үш параметрдің төмендегі қатынасы молекулалардың әсерлесуін сипаттайтын шамалармен байланысы тіптен жоқ.
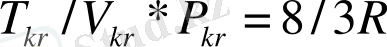 (9)
(9)
Қатынас тек газдардың универсал тұрақтысына ғана кері пропорционал.
Бұдан біз мынадай қортынды шығаруымызға болады: жоғарыда барлық инертті газдар үшін көрсетілген біртұтас келісілген масштабты схема осы газдардағы кризистік құбылыстар үшін де орындалады. Бұл тұжырымның дұрыс екендігіне төменгі 3- кестеде келтірілген шамалардың мәндерінен көз жеткізуге болады. Бұл таблицада инертті газдардың кризистік нүктесін анықтайтын
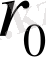 , W параметрлері бойынша алынған келтірілген мәндері берілген.
, W параметрлері бойынша алынған келтірілген мәндері берілген.
3 Кесте. Кризистік параметрлер және олардың келтірілген мәндері
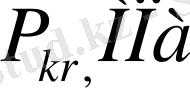
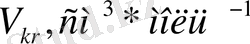
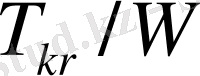
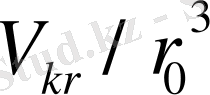
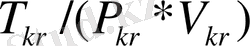
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz