Термодинамиканың негізі

Жоспар

Термодинамиканың негізі.
1. Термодинамиканың мақсаты. Негізгі түсініктер.
2. Ішкі энергия ұғымы.
3. Ішкі энергияны өзгертудің әдістері.
4. Идеал газдың ішкі энергиясын есептеу.
5. Идеал газдың жылу сыйымдылықтарының ұғымы.
1.6. Термодинамиканың бірінші бастамасы
1.7. Термодинамиканың бірінші бастамасын изопроцестерде қолдану
1.7.1. ИЗОХОРАЛЫҚ ПРОЦЕСС
1.7.2. ИЗОБАРАЛЫҚ ПРОЦЕСС
1.7.3. ИЗОТЕРМИЯЛЫҚ ПРОЦЕСС
1.7.4. АДИАБАТАЛЫҚ ПРОЦЕСС
1.7.5. ПОЛИТРОПТЫ ПРОЦЕССТЕР.
1.8. Дөңгелек цикл.
1.8.1. ҚАЙТЫМДЫ ЖӘНЕ ҚАЙТЫМСЫЗ ПРОЦЕССТЕР.
1.9.Термодинамиканың екінші бастамасы.
1.10. Карно циклы және идеал газ үшін оның пайдалы әсер коэффициенті

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

Термодинамиканың негізі.
1.1. Термодинамиканың мақсаты. Негізгі түсініктер.
Молекулалық физиканың басты тарауының бірі- термодинамика.
Термодинамика ХIХ ғасырдың бірінші жартысында енді ғана дами бастаған
жылу техникасының теориялық негізі ретінде пайда болды. Оның бастапқы
мақсатының бірі жылу двигательдерінде жылудың механикалық жұмысқа айналуын
зерттеу болды. Кейінірек термодинамиканың зерреу пәнінің ауқымы кеңіді де,
материя қозғалысының жылулық формасының бір түрден екінші түрге айналуын,
жылудың бір денеден екіншіге берілуін, осы кездегі физикалық процесті
тексерді.
Термодинамика негізінен денелердің термодинамикалық тепе-теңдік күйін
қарастырады.
Уақыт өзгергенмен термодинамикалық жүйенің күйі, яғни оны сипаттайтын
параметрлер тұрақты болса, оны термодинамикалық тепе-теңдік деп атайды.
Бұған мысал ретінде су буланғанда одан ұшып шығатын молекулалар мен
будың, конденсацияланған кезде суға қайтып келетін молекулаларының санының
тең болуын айтуға болады. Бұл термодинамикалық тепе-теңдікті динамикалық
теңдік деп атайды.
Термодинамикалық жүйе деп бір-бірімен механикалық және жылулық прцесс
түрінде әсерлесіп зат алмасатын материалдық нүктелер (сол сияқты өрістер)
жиынтығын айтады.
Заттар әртүрлі агрегаттық күйіне қарай оларды газ, сұйық, қатты және
плазмалы фаза деп бөледі.
Заттың бір фазасынан тұратын жүйені гомогенді деп атайды.
Бір-бірінен бөлуші жазықтықтар арқылы ажыратылған әртүрлі гомогендік
бөлшектерден тұратын жүйені гетерогенді деп атайды.
Жүйенің термодинамикалық тепе-теңдік күйге өздігінен өту процесін
релаксация деп атайды да, оған кеткен уақытты релаксация уақыты деп атайды.
Термодинамика үш заңға сүйенеді (мұны үш бастама деп те айтады).
Біріншісі термодинамикалық құбылыстарға энергияның сақталу заңының
қолданылуын түсіндірсе, екіншісі термодинамикалық процесстердің өту бағытын
сипаттайд, ал үшінші бастамасы температура абсолют ноль болғанда кез-келген
фазасының энтропиясы нольге айналатындығын дәлеледейді.
1.2. Ішкі энергия ұғымы.
Барлық денелерді механикалық энергиямен сипаттаған сияқты, оларды ішкі
күйлеріне тәуәлді энергиямен де түсіндіруге болады.
Денені құрайтын бөлшектердің қозғалысымен өзара әсерлесуін сипаттайтын
бұл энергияны ішкі энергия деп атайды.
Оны денедегі молекулалар мен атомдардың жылулық қозғаласының кинетикалық
энергиясы, молекуладағы атомдар мен электрондардың әсерлесуінің
потенциалдық энергиясы, т.б. құрайды.
Ішкі энергия дененің немесе жүйенің күйін сипаттайтын шамалардың
жиынтығы арқылы анықталады, сондықтан ол жүйе күйінің функциясы болады да,
W әрпімен белгіленеді.
Температурасы аса жоғары немесе аса төмен емес денелердің ішкі энергиясы
осы дене молекулаларының масса центріне қатысты ретсіз жылулық
қозғалыстарынң кинетикалық энергиясы мен сол молекулалардың өзара
әсерлесуінің потенциалдық энергиялардың қосындысынан тұрады.
Ішкі энергия дене күйінің функциясы болғандықтан, температура өзгерген
сайын ол да өзгереді, айталық температура артса ішкі энергия энергия
көбейеді, температура кемісе энергия азаяды.
Ішкі энергияны денені деформациялау арқылы немесе бір агрегаттық күйден
екіншіге көшіру арқылы да өзгертуге де болады. Өйткені бұл кезде дене
молекулаларының ара қашықтығы өзгереді де, потенциалдық энергия азайып
немесе көбейеді.
1.3. Ішкі энергияны өзгертудің әдістері.
Дененің ішкі энергиясын екі жолмен өзгертеді. Мысалы, сыртқы күштер
денені қозғап механикалық әсер бергенде жұмыс істеу арқылы ( кейде дене
көлемін өзгерту үшін өзі сыртқы күштерге қарсы жұмыс істейді)болса, екінші
жолы жұмыс істемей-ақ дене өзінен температурасы жоғары немесе төмен
денелермен жанасқанда жылу алмасу арқылы өзгерту.
Дененің ішкі энергиясын механикалық жұмыс істемей өзгерту прцесін жылу
алмасу немесе жылу беру деп атайды.
Жылу беру конвекция, жылу өткізгіштік және сәуле шығару деп үшке
бөлінеді.
Бірақ жұмыс пен жылу алмасу арасында елерліктей айырмашылық бар.
Энергияны өзгертуде жұмыс жан-жақты роль атқарады, әрі негізгі формасы
болады. Жұмыс істелгенде энергияныің әр түрі бір-біріне ауыса береді,
айталық газды қысқанда механикалық энергияға айналса, газ ұлғайғанда ішкі
энергия механикалық энергияға ауысады.
Ішкі энергияны өзгерткенде істелетін жұмыс шамасын табайық. Ол үшін
жұмысшы денесі ретінде газды алып, оның көлемін азайтайық. Сонда газдың
қысым күшіне қарсы жұмыс істеледі. Цилиндр ішіндегі газдың көлемін
поршеньнің қозғалысы арқылы (1-сурет) өзгертеміз. Ауданы S поршеньге қысымы
Р газдың әсер ету күші F=PS болғандықтан, поршень dx аралықта қозғалғанда
істелетін жұмыс

dA=PSdx=PdV                (3.1)       мұнда dV=Sdx газ көлемінің
өзгерісі.

1-сурет.
Газдың жұмысы оның қысымы мен көлем өзгерісінің көбейтіндісіне тең.
Дұрысында жоғарыдағы формуланы
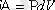                                                             (3.2)
деп жазған орынды, өйткені шексіз аз шаманы 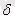мен белгілеу, ал кез-
келген нәрсенің аз өзгерісі дегенді d таңбамен белгілеу келісілген.
Сондықтан болар-болмас істелген аз жұмысты 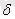А деп, көлем өзгерісін
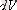арқылы белгілейміз.
Газдың көлемі V1 -ден V2 -ге дейін өзгергенде істелетін жалпы жұмысты
табу үшін    (3.1) формуланы интегралдаймыз:
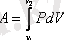                                                        (3.3)

1. 4. Идеал газдың ішкі энергиясын есептеу.
Газ әртүрлі жылдамдықпен қозғалатын, олай болса белгілі кинетикалық
энергиясы бар молекулалардан тұрады.
Барлық газ молекулаларының толық энергиясы газдың ішкі энергиясы деп
аталады.
Жалпы газдың ішкі энергиясы молекулалардың барлық энергияларының
қосындысына тең. Идеал газдың молекулалары бір-бірімен
әсерлеспегендіктен,олардың потенциалдық энергиясы болмайды.Сондықтан идеал
газ молекуласының толық энергиясы сол молекулалардың
ілгермелі,айналмалы,кейде тербелмелі қозғалыстарының кинетикалық
энергияларының қосындысынан тұрады.
Дененің ілгермелі қозғалысын координат жүйесінің үш оснің бойымен
болатын бір-біріне тәуелсіз үш қозғалысқа жіктеуге болады.Максвеллдің
ұсынуы бойынша бұл тәуелсіз қозғалыстарды молеула қозғалысының еркіндік
дәрежесі деп атайды.Еркіндік дәрежесінің саны тәуелсіз координаттарының
санына тең.Олай болса еркіндік дәрежесі деп дененің(молекуланың)
кеңістіктегі орнын анықтайтын тәуелсіз координаттардың санын айтады.
Ілгермелі қозғалатын кез-келген молекуланың еркіндік дәрежесі
үшеу.Молекуланың классикалық кинетикалық теориясы бойынша бір атомнан
тұратын ондай молекула идеал тегіс қатты шар деп алынады да, ол
соқтығысқанда да айналмалы қозғалмай, тек ілгермелі қозғалады.Сондықтан
ілгермелі қозғалатын бір атомды молекуланың үш еркіндік дәрежесі бар деп
қорытындылаймыз.
Екі атомды молеуланың бір айналу осі молекуланың осімен сәйкес
келгендіктен, оның еркіндік дәрежесі 5-ке тең(өйткені ілгермелі
қозғалысының еркіндік дәрежесі үшеу де, айналмалы қозғалысінікі екеу).Олай
болса екі атомды молекуланың кеңістіктегі орнын анықтау үшін оның ауырлық
центрінің үшк координатын (xi,yi,zi) және екі айналу бұрышын беру
қажет (1-сурет).

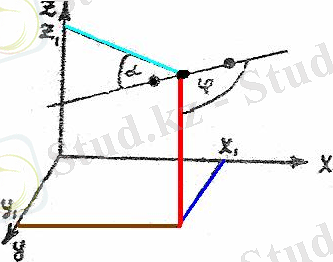
1-сурет.
Молекуланың ретсіз (хаосты) қозғалуы тек ілгермелі қозғалысқа ғана
тәуелді емес, сонымен бірге айналған, тербелген молекулаларға да ретсіздік
қозғалыс тән және осы бағыттардың бір-бірінен артықшылығы жоқ, ал бұл
ілгермелі қозғалған молекуланың үш еркіндік дәрежесіне де, энергияның
бөлінуінд ешқандай артықшылық жоқ деген ұғымға әкеледі. Сондықтан бұл
ұғымды Больцман молекуланың әрбір еркіндік жәрежесіне орташа шамамен бірдей
энергия келеді деп қорытты.Мұны энергияның еркіндік дәрежеге біркелкі
таралуының Больцман теоремасы деп атайды. Бір еркіндік дәрежеге келетін
орташа кинетикалық энергияны есептеу үшін 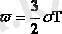формуланы пайдаланамыз.
Бұл еркіндік дәрежесі үшке тең бір атомды молекуланың (материалдық нүктенің
энергиясы, онда еркіндік дәрежесі бірге тең молекуланың энергиясы( )
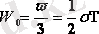болады.     (4.1)
Онда Больцман теоремасы бойынша еркіндік дәрежесі болатын
молекуланың толық кинетикалық энергиясы
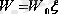немесе 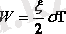           (4.2)
Осы формуладае температураның абсолют нолінің физикалық мәнін шығаруға
болады: T=0, энергияда W=0, яғни температура абсолют ноль болғанда газ
молекуласының қозғалысы тоқтайды.
1 кмоль газдың толық кинетикалық энергиясы бір молекуланың энегиясынан
N есе артық (N – 1 кмольдағы молекула саны және осы мөлшердегі газ үшін
n=N):
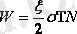, мұнда N=R
Осыны орнына қойсақ 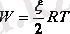                         (4.3)
Идеал газ молекулаларының өзара әсерлесу күшін ескермегендіктен, оның
ішкі энергиясы (W) сол газдың кинетикалық энергиясын ғана сипаттайды. Олай
болса 1 кмоль идеал газдың ішкі энергиясы
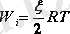болады.                        (4.4)
Кез-келген массалы (m) газ үшін (осы газдың киломолінің саны ,
-бір киломольдің массасы) жоғарыдағы формуланы төмендегіше жазамыз:
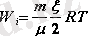                              (4.5)
Массасы кез-келген мөлшердегі газдың ішкі энергиясы молекуланың
еркіндік дәрежесінің санына, оның абсолют температурасы мен массасына тура
пропорционал.
1.5. Идеал газдың жылу сыйымдылықтарының ұғымы.
Кез-келген дененің (газдың) жылу сыйымдылығының өрнегін табу үшін ішкі
энергия ұғымын пайдаланамыз.
Жылу сыйымдылық қыздырылатын заттың массасына байланысты төмендегіше
бөлінеді.
Массасы кез-келген мәнді дененің температурасын 10К-ге арттыруға қажет
жылу мөлшерін жылу сыйымдылық деп атайды. Біртекті денелердің жылулық
қасиетін меншікті және мольдік жылу сыйымдылықтарымен сипаттайды.
Массасы 1 кг дененің температурасын 10К-ге арттыруға қажет жылу
мөлшерін меншікті жылу сыйымдылық деп атайды да С әрпімен белгілейді. Оны
орта мектеп курсынан белгілі жылу мөлшерінің формуласынан табады:
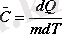                              (5.1)
dQ – массасы m денеге берілетін жылу мөлшері. dT – дене
температурасының өзгерісі. Нақта денелер мен газдың меншікті жылу
сыйымдылығы температураға тәуелді болғандықтан, соңғы формула дифференциал
түрінде жазылады.
Дененің бір молінің температурасын 10К-ге арттыруға қажет жылу мөлшерін
мольдік жылу сыйымдылық деп атайды( ).
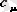Осы анықтамалардан меншікті және мольдік жылу сыйымдылықтардың
арасындағы байланысты төмендегіше жазамыз:
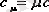       , - заттың мольдік массасы.
Соңғы өрнекке (10-9) формуласын қойсақ
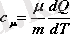               шығады.         (5.2)
Бұдан 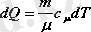   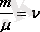   ,            - зат мөлшері.       (5.3)
Газдың жылу сыйымдылығы оның қыздырылу шарттына, дәлірек айтсақ қысым
мен көлемнің тұрақты болуына байланысты.Газды тұрақты көлемде қыздырсақ,
онда газға берілген жылу толықтай оның ішкі энергиясын арттыруға
кетеді.Тұрақты қысымда қаздырғанда газ ұлғайып жұмыс істейді,сол үшін
қосымша жылу мөлшері қажет,өйткені көлем артады. Сондықтан газды екі түрлі
мольдік және меншікті:тұрақты көлемдегі (сv) және тұрақты қысымдағы (ср)
жылу сыйымдылықтармен сипаттайды. Жоғарыдағы түсініктерден ср сv
болатындығы түсінікті.
Газды тұрақты көлемде қыздырғанда жылу толықтай оның ішкі энергиясын
арттыруға кететіндіктен, газдың тұрақты көлемдегі мольдік жылу сыйымдылығын
ішкі энергияның өзгерісінің (∆ 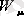)температураға өзгерісіне (∆Т)
қатынасы ретінде жазамыз:
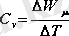                                          (5.4)
(4.4) формуланы ескерсек ( 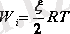) ,онда
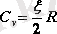                                (5.5)
ал меншікті жылу сыйымдылығы
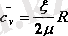                              (5.6)
Газды тұрақты қысымда қыздырғанды қосымша жұмыс істелендіктен Ср=Cv+A
деп жазамыз.                                             (5.7)
Осы жұмысты есептей отырып, оның газды тұрақты қысымда 10К-ге
қыздырғанда сол газдың мольдік тұрақтысына (R) тең болатындығы анықталды,
яғни A=R , онда Ср=Cv+R, (5.7) бұл Роберт Майер формуласы деп аталады (бұл
формуланы кейін қорытып шығарамыз). Осындағы Cv орнына (5.5) өрнегін
қойсақ
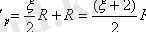                   (5.8)

Соңғы формуланы (5.5) өрнегіне бөліп , жылу сыйымдылықтарының
қатынасын 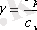    арқылы белгілесек
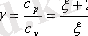     (5.9)
1 және ол газдың табиғатына (еркіндік дәрежесіне) байланысты
1.6. Термодинамиканың бірінші бастамасы.
Жүйені құрайтын денелердің микроскопиялық құрылысын ескермей, бір-
бірімен энергия алмасатын жүйелердегі физикалық процесстерді қарастыратын
физиканың тарауы- термодинамика.
Термодинамиканың бірінші бастамасы жылулық процесстерге қолданылатын
энергияның сақталу заңының жалпылама түрі деп қарастырылады және энергияның
сандық және сапалық түрінің бір-біріне түрленуін сипаттайды.
Ішкі энергиясы W1 газ сырттан Q жылу алады, сөйтіп өзінің ішкі
энергиясын W2 шамаға өзгертіп A жұмыс істейді.
Келісім бойынша жүйенің алған жылуын оң, жүйенің сыртқы күштерге қарсы
істегенжұмысын да оң мәнді деп есептейді. Энергияның сақталу заңына сәйкес
жүйе бір күйден екінші күйге қандай әдіспен өтсе де оның ішкі энергиясының
өзгеруі ∆ W= W2 - W1 бірдей, әр жүйенің алған жылуы мен (Q) жүйенің сыртқы
күштерге қарсы істеген жұмысының (А) айырымына тең:
∆ W= Q- A немесе Q=∆ W+ A               (6,1)

(6,1) өрнегі термодинамиканың бірінші бастамасының математикалық
теңдеуі (Q, A және ішкі энергия бірлікпен өлшенеді).ол былай оқылады:
жүйеге берілген барлық жылу оның ішкі энергиясын арттыруға және жүйенің
жұмыс істеуіне кетеді.
Егер жүйеге берілген шексіз аз жылу (δQ) салдарынан оның ішкі
энергиясын аз шамаға (d W) өзгеріп, шексіз аз, яғни болар-болмас жұмыс
істесе (δА),онда термодинамиканың бірінші бастамасының өрнегін осыған
сәйкес нақты түрде былай жазады:
δQ= d W+ δА                                         (6,2)
Бірақ бұл өрнекті көбіне толық дифференциал түрінде жазады:
dQ= d W+ dА                                           (6,3)
және осыны термодинамиканың бірінші бастамасының өрнегі деп
қабылдаймыз.Соңғы формуладан жылу да жұмыс пен энергия сияқты джоульмен
(Дж) өлшенетіні байқаймыз.(6,1) энергияның сақталу заңының салдары ретінде
жазылды.Оны төмендегі түрде де жазуға болады:
∆ W= Q+ A’
(6,4)
мұнда A’ – сыртқы күштердің жүйенің (газдың) кедергісін жеңуге қарсы
істеген жұмысы. Олай болса жүйенің (газдың) ішкі энергиясын сырттан алған
жылу (немесе оны қыздыру) және сыртқы күштердің жұмысы арқылы арттыруға
болады (газды қысқанда сыртқы күштер жұмыс істейді де , газ қызады, олай
болса оның ішкі энергиясы артады).
Егер жүйе (газ) периодты түрде бастапқы қалпына оралса, оның ішкі
энергиясының өзгерісі ∆ W=0. Ендеше (6,1) формуладан
А= Q                                                  (6,5)
Термодинамиканың бірінші бастамасынан , әрі (6,5) формуладан да көрініп
тұрғандай сырттан берілген энергиядан артықжұмыс істейтін периодты
қайталанып отыратын машина жасауға болмайды(термодинамиканың бірінші
бастамасының екінші түрлі анықтамасы), яғни мәңгілік двигателдің бірінші
түрін жасау мүмкін емес , әйтпесе AQ болар еді.
1.7. Термодинамиканың бірінші бастамасын изопроцестерде қолдану.
Термодинамикалық жүйелерде орын алатын тепе-тең процесстердің ішінде
үнемі бір параметрі(шамасы) тұрақты болатын изопроцесстердің орны
ерекше.Біз осы процесстерді термодинамиканың бірінші бастамасы арқылы қалай
сипаттауға болатынын қарастырайық.
1.7.1. ИЗОХОРАЛЫҚ ПРОЦЕСС
Бұл кезде идеал газдың көлемі (V=const) тұрақты болады.(1-сурет.)

1-сурет.
Қыздырғанда газ ұлғаймас үшін, оның қысымын Р0-ден Р-ға дейін арттрамыз.Р –
V диаграммасында бұл процесс ордината осіне параллель түзімен
кескінделеді.Изохоралық қыздыру 1-2 түзумен, изохоралық суыну 1-3 түзумен
сипатталады (1-сурет).Изохоралық процессте (исос-тең, хорема-
сыйымдылық) газ жұмыс істемейді, олай болса берілген жылу толығымен газдың
ішкі энергиясын арттыруға(өзгертуге) жұмасалады.
Сонымен
                 dA=PdV=0 болғандықтан, термодинамиканың бірінші
бастамасынан Q=∆W немесе dQ=dW (7,1) деп жазамыз.(5,1) формуладан dQ=cvmdT
(7,1) өрнегін ескерсек, изохоралық процесс кезіндегі ішкі энергияның
өзгерісін де жазуға болады:
dW=cvmdT       (7,2)
Бұл Джоуль заңының дифференциал түрі, cv – изохоралық процесстегі газдың
мольдік жылу сыйымдылығы.
        Газды Т0-ден Т температураға бейін изохоралы қыздырғанда ішкі
энергияның өзгерісін соңғы формуланы интегралдау арқылы табамыз:
∆W1-2=W-W0=cvm(T-T0)                (7,3)
        Температура абсолют ноль болғанда идеал газдың ішкі энергиясының
нольге айналатындығын ескерсек (T0=0 болса, W0=0):
W=cvm T                                (7,4)
газдың ішкі энергиясы температуға тәуелді.

1.7.2. ИЗОБАРАЛЫҚ ПРОЦЕСС
Тұрақты қысымда өтетін процессті (Р=const) изобаралық деп атайды
(грекше) (исос-тең, барос-ауыр,салмақ).(10-9) өрнекті пайдаланып,
изобаралық процесс кезіндегі жылу өзгерісін жазайық:
dQ=cрmdT                                   (7,5)
Осыны және (7,2) формуланы термодинамиканың бірінші заңының (10-21)
орнына қойсақ: cрmdT=cvmdT+ dA, бұдан бұрынырақ

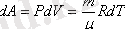
болатындығы айтылған еді, осыны ескерсек

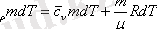
mdT шамасына қысқартқаннан кейін    = + , енді меншікті
және мольдік жылу сыйымдылықтар арасындағы байланысты (10-10) ескерсек,
онда жоғарыдағы өрнекті мольдік жылу сыйымдылық арқылы төмендегіше жазамыз:
CP-CV=R                             (7,6)
Бұл мольдік изобаралық және изохоралық жылу сыйымдылықтар арасындағы
байланысты беретін Роберт-Майер (1814-1878 ж.ж неміс дәрігері, физигі)
формуласы.
Изобаралық процессте газды қыздырғанда ол ұлғайып, берілген жылудың бір
бөлігі газдың ішкі энергиясын арттыруға, қалғаны сыртқы күштерге қарсы
газдың жұмыс істеуіне жұмсалады.
Осы кездегі жұмысты есептейік.
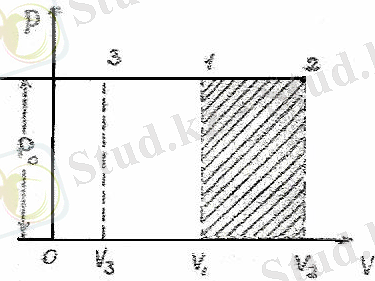
2-сурет.
Изобаралық процесске мысал ретіндегі цилиндрдегі газға қозғалмалы
поршень арқылы эсер ететін тұрақты сыртқы қысымды алүға болады.
2-суретте қыздырғанда газдың изобаралық ұлғаюы(1-2 түзу) және
изобаралық сығылуы (1-3 түзу ) көрсетілген.Сонымен изобаралық ұлғаюы
кезіндегі жұмысты 2-сурет арқылы жазамыз:
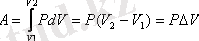            (7,7)
Сонымен, газдың изобаралық ұлғаюы кезіндегі жұмысы оның қысымы мен
көлемінің өсімшесінің көбейтіндісіне тең және ол диаграммада V112 V2 тік
төртбұрыштың ауданына тең. Изобара 1-2 түзу сызықпен кескінделеді.
Изобаралық процесс кезіндегі мольдік жылу сыйымдылықты табу үшін Роберт-
Майер формуласына изохоралық процесстің мольдік жылу сыйымдылығының (
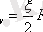)мәнін қояйық:
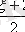cp-cv=R, cp- R=R , cp=R( )          (7,8),
ал   изобаралық процесстің меншікті жылу сыйымдылығы
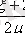=( )R                     (7,9)
1.7.3. ИЗОТЕРМИЯЛЫҚ ПРОЦЕСС
        Тұрақты температурада жүретін процессті изотермиялық деп атайды
(грекше термос-жылу). (Т=const) болғандықтан, газдың ішкі энергиясы
өзгермейді,яғни dW=0.
        Онда термодинамиканың бірінші заңы dQ= dA болады,яғни газды
изотермиялық қыздырғанда оған берілген барлық жылу сыртқы күштерге қарсы
жұмыс істеуге кетеді.
        Газдың шексіз аз ұлғайған кезіндегігі жұмысын dA табайық,өйткені
бұл кезде қысымның өзгерісін ескермей тұрақты деп алуға болады, (7,7)
бойынша dA=PdV.
         Газдың кез-келген массасы үшін жазылған Клапейрон-Менделеев
теңдеуіне қысымды тауып, жоғарыдағы формулаға қоямыз: PV= RT
бойынша
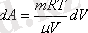
        Газдың V1-ден V2-ге ұлғайған кездегі толық жұмысын табу үшін, соңғы
өрнекті интегралдаймыз:
A= 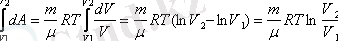    (7,10)
          Бойль-Мариотт заңы бойынша 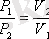   болғандықтан

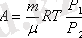
немесе         dQ= dA ескерсек
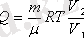(7,11)
(7,10), (7,11) формулаларды салыстыра отырып мынадай физикалық қорытынды
жасауға болады:
          газдың ұлғаюы кезінде температура төмендемес үшін, прцесстің өн
бойында газға сыртқы ұлғаю жұмысына тең жылу беріп тұру қажет.

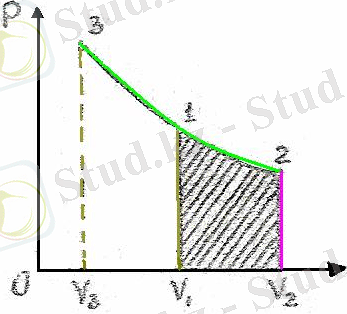
3-сурет.
         Газ изотермиялық ұлғайғанда (V2 V1графикте 1-2 қисығы), оған
жылу беріледі де (Q0), газдың жұмысы оң мәнді (A0) болады, ол 3 суреттегі
боялған ауданға тең.
Газ изотермиялық сығылғанда (графикте 1-3 қисығы), оның жасаған жұмысы
теріс мәнді (A1-20), бұл кезде газдан осы сығылу ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.