Графикалық торлар

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Графикалық торлар

Графикалық торлар-бұл техника мен ұйымдастыру жүйелерді графика арқылы көрсету әдісі. Ғылыми жұмыстарды графикамен көркемдеу нақты мәнін көрнекілігімен көрсетеді, кей жағдайда қойылған міндеттің шешімін табуды тіпті жеңілдетеді. Әр түрлі көрнекілікті графикамен көрсетудің әмбебап құралы ретінде граф табылады. Мұнда граф деп, торап пен қырлардың жиынтығын түсінеді. (4. 6-сурет) . Түрлі торап пен қабырғалардың сан алуан құрамалары, мүмкін болатын графтар мен олардың қолдану жолдарын көрсетеді. Қабырға бағыттары көрсетілмеген, ал тораптар төртбұрыш түріне келтірілген графтар техникалық жүйелердің құрылымын көрсетуге қолданылатын блоксхемаларды суреттейді. 4. 6-суретте көрсетілген графты ағаш деп атайды. Мұндай ағаш-граф арқылы толық санды бағдарламалау міндетін қарастыратын бұтақтар мен шекаралар әдісін қөркемдейді. Егер ағаштағы баоылық тораптар бірнеше деңгейге бөлінсе, онда оны көп деңгейлі иерархия жүйесі деп білеміз. Егер граф қабырғасы бағытқа ие болса, яғни доға арқылы жүзеге асса, ондай графты тор деп атайды. Тор арқылы орын ауыстыру немесе уақыт бойында орындалатын жұмыстардың тиімді шешімін табудың түрлі міндеттері көрсетіледі. Тор доғалардың құрылым мен параметрлері сипатталады. Тор құрылымы, немесе оны топология деп атайды, байланысшы доғалардың юағытын және тораптарын өзара қалай байланысатынын көрсетеді. Әрбір торапты реттік санмен белгілейді. Бастапқы торапты бастау деп, ал соңғысын ағаш деп атайды.

4. 6-сурет

Доғаны қосарланған индекспен белгілеиді. Жалпы i-j деп көрсетеді, онда i доға шығатын тораптың нөмеірі, j-доға кіретін торап нөмірі деп қабылданады. Әрбір доға өз сипатына ие болады. Мысалы, t _i - j доға бойымен қозғалу мерізімі, c _i -j- орын ауыстыру құны, d _i -j доғаның өткізу қабілеті, т. б.

. 7-сурет

Тордың құрылымын және доға сипатын біле отырып, ғылыми-ерттеулерде жиі кездесетін түрлі есептерді шешуге болады.

Жылжу есептері.

а) Коммивояжер есебі 4. 8-суретте көрсетілгендей, орналасқан 5 пункт бар, олардың бір-бірімен байланыс арқылы әр бір пункттен кез келген басқа пунктке өтуге болады. Мұнда қойылатын талап: белгілі бір пункттен шығып ең аз уақыт ішінде барлық пункттерді айналып шығу.

4. 8-сурет

Бұл есепті шешу үшін математикалық модель құраймыз. Ол үшін белгілерді енгіземіз:i және j-кіру-шығу пункттерір нөмірі, t _ij - I пунктіне жүру уақыты 4. 10-кестеден көрінетіндей, tij жалпы кері бағыттағы tij уақытына тең болмайды.

4. 10-кесте

I пунктінен

J пунктіне

I пунктінен: 1

J пунктіне: 0

I пунктінен: 2

J пунктіне: 1

I пунктінен: 3

J пунктіне: 8

I пунктінен: 4

J пунктіне: 14

I пунктінен: 5

J пунктіне: 10

Математикалық модельді құру үшін бізге белгілі қисынды буль ауыспалы мәндерді аламыз.

\[\delta_{i j}=\stackrel{\downarrow}{\downarrow}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\phantom{j}\hat{a}\partial^{j}\hat{a}\quad\stackrel{\textstyle\enspace\alpha\sigma\partial\hat{a}\hat{a}}{\hat{a}\hat{a}}\quad\stackrel{\alpha\sigma\partial\hat{a}}{\partial\hat{a}\hat{a}}\]

деп қабылдаймыз.

4. 9-сурет

4. 9-сурет

Модель құраймыз. Пункт 1-ден кез-келген төрт пункттің бірекіне шығуға немесе осы пункттің өзінде қалуға болады. (4. 9-сурет) . Бұл жағдайда бір бағытта шығуға болады. Бұл шартты мынадай түрде жазамыз:

δ ₁₁ +δ ₁₂ +δ ₁₃ +δ ₁₄ +δ ₁₅ =1

жалпы бұл шарт былай жазылады:

₅

∑δ

j-1

Егер пункт 1-ден кез келген i-пунктіне шығатын болсақ, онда ол былай көрсетіледі:

5

∑ δ _ij =1, i=1, 5 (4. 14)

j=1

Бұл тәуелділіктер бастапқы талапты орындауға мүмкіндік береді: әрбір пункттен тек бір қана және бір бағытта жүруге болады. Бағдартың ең аз ұзақтық талабын мақсатты функция түрінде жазамыз:

А=t ₁₁ δ ₁₁ +t1 ₁₂ δ ₁₂ +t ₁₃ δ ₁₃ +t ₁₄ δ ₁₄ +t ₁₅ δ ₁₅ t+t ₂₁ δ ₂₁ +t ₂₂ δ ₂₂ + . . . +t ₅₅ δ _{55→ min,} (4. 15)

Мұнда tij мәндері 4. 10-кестеден алынады, ал δij ізделіеген ауыспалы мәндер болып келеді. Жазудың қысқартылған түріне көшсек, ол огсындай болады:

(4. 16. )

Жүйе шешу нәтежесінде (4. 16) келесі мәндерді аламыз: δ ₁₅ =δ ₅₂ +δ ₂₃ +δ ₃₄ +δ ₄₁ =1 қалғаны F=10+8+10+20+14=62 болады. Бұл бағдар 4. 10-суретте көрсетілген.

4. 10-сурет

4. 11-сурет

Егер жеке жағдайдан айырылсақ, есептің n пункттердің айналып шығу жалпы талабын орындау үшін былай жазамыз:

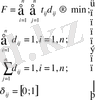
(4. 17. )

Сонымен қоса 4. 16 және 4. 17 шарттарды қанағаттандыратын бағдар бар: жылжу барысында үзілістер болады, бірақ әр пункттен бір рет кіріп-шығу шарты орындалады (4. 11-сурет) . (4. 16) және (4. 17( жүйесі қажетті, бірақ жеткіліксіз шарттарды қамтиды. Ол үшін қосымша N шектеулер енгізіледі: N=(n-1) ²-(n-1), әр бір шектеу мынадай түрде болады:

Y _i -y _j nδ _ij ≤n-1; i=2, n; j=2, n-∞<y _ij <∞.

(4. 18)

Біздің мысалда мұндай қосымша шектеулер саны N=(5-1) ²-(5-1) =12 тең болады. Олардың түрі мынадай болып келеді.

Y ₂ − y ₃ + 5δ ₂₃ ≤ 4 ; y ₂ − y ₄ + 5δ _{2 4} ≤ 4 ; y ₂ - y ₅ + 5δ ₂₅ ≤ 4 ;

Y ₃ - y ₂ + 5δ ₃₂ ≤ 4 ; . . . ; y ₅ - y ₄ +5δ ₅₄ ≤4.

Сонымен есептің математикалық моделі ретінде (4. 17) жүйесі мен қосымша шектеулер (4. 18) сеналады. Осындай коммивояжер есебі тәріздес ғылыми мәселерді шешуде туындайтын көптеген есептер бар-қайсыбір бұйымды өндеудің технологиялық үрдісін тиімді ұйымдастыру, базаларды қамтамасыздандыру, ұйымдастыру және т. б.

б) Ең қысқа жолды іздеу есебі. 4. 12-суретте көрсетілгендей А пунктінен В пунктіне көп жолдар барады.

4. 12-сурет

Кейбір жолдарда қозғалыс бір жақты, кейбіреуінде екі жақты. Екі пунктің арасындағы жол ұзындығы әрбір доғада көрсетілген. сонда А пунктінен В пунктіне ең қысқа жол табу қажет. Математикалық модель құраймыз. 4. 13-суретте көрсетілгендей пунктіне кіретін-шығатын доғаларды болжаймдайық:

4. 13-сурет

Бағдар үзіліссіз болу үшін әрбір пунктке тек бір доға кіріп-шығу керек. Бұл талап егер төмендегідей шарттар болса орындалады: Пунктке кіретін доғалар үшін:

p

Nibx=∑δ _kj =1 (4. 19)

k=1

Мұнда δk _i k пунктінен шығатын және i пунктіне кіретін доғағак сәйкес келеді.

\[\delta k_{i}=\frac{11}{1}.\tilde{a}\hat{a}\hat{a}\partial\bar{a}\bar{u}\bar{u}\bar{a}\dot{a}\,k-\,i\,\hat{a}\bar{a}\bar{a}\partial\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\bar{a}\]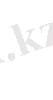

(4. 19) шарт i пункітінен шығатын және j тіне кіретін доғаға сәйкес келеді:

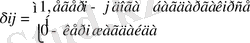
(4. 20) шарты i пунктіне тек бір доғамен шығуды қамтиды.

Бағдардың барлық пунктерін бастапқы, өткелі және соңғы деп бөлуге болады.

Бұл пункттер үшін келесі шарт орындалу керек.

(4. 21)

Шынымен, бастапқы пуект N _вх =0. Демек, бастапқы пункттен тек бір доға шығу керек. Өткелі пункттер үшін N _iвх =N _iвых шарт бір доғамен шеғу-кіруді қамтиды. Соңғы пункт үшін N _вых = 0 кіруді бір

доғамен қамтиды. Сонымен (4. 20-4. 21) шарттары үзіліссіз бағдар талабын орындайды. Мұнымен қатар бағдар ең аз ұзындыққа ие болу үшін мақсатты функцияны қосамыз:

F=∑ ∑ C _ij δ _ij (4. 22)

i j

Мұнда C _ij -жол ұзындығы, ол барлық доғаларды қамтиды "Шектеулер" мен мақсатты функцияны қосқанда жүйені былай жазамыз:

F= ∑ ∑C _ij δ _ij →min

i j

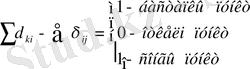
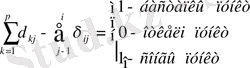
δ _ij ≥ 0

бұл ауыспалы мәндерге теріс емес талабының қойылғаны жеткілікті, яғыни δ _ij ≥ 0.

δ _ij = 0 немесе δ _ij = 1 талабын қоймаса да болады, себебі мұндай есептерде шектеулер арқасында шешу барысында δ _ij тек 0 немесе 1 мәнін алуды қамтиды.

4. 12 берілген суреттегі есепке 4. 23 жүйесін құраймыз, ыңғайлы болу үшін бұл жүйені 4. 11-кесте ретінде көрсетеміз.

Пункт

δ ₁₂

δ ₁₃

δ ₁₄

δ ₂₃

δ ₂₅

δ ₃₂

Δ ₃₄

δ ₃₅

δ ₄₃

δ ₄₅

белгі

Оң жол

Пункт: F

δ12: 2

δ13: 6

δ14: 8

δ23: 3

δ25: 7

δ32: 5

Δ34: 1

δ35: 5

δ43: 4

δ45: 2

белгі: min

Оң жол:

Пункт: 1

δ12: -1

δ13: -1

δ14: -1

δ23:

δ25:

δ32:

Δ34:

δ35:

δ43:

δ45:

белгі: =

Оң жол: -1

Пункт: 2

δ12: 1

δ13:

δ14:

δ23: -1

δ25: -1

δ32: 1

Δ34:

δ35:

δ43:

δ45:

белгі: =

Оң жол: 0

Пункт: 3

δ12:

δ13: 1

δ14:

δ23: 1

δ25:

δ32: -1

Δ34: -1

δ35: -1

δ43: 1

δ45:

белгі: =

Оң жол: 0

Пункт: 4

δ12:

δ13:

δ14:

δ23:

δ25:

δ32:

Δ34: 1

δ35:

δ43: -1

δ45: -1

белгі: =

Оң жол: 0

Пункт: 5

δ12:

δ13:

δ14:

δ23:

δ25: 1

δ32:

Δ34:

δ35: 1

δ43:

δ45: 1

белгі: =

Оң жол: 1

Мұндай әрбір доғаға ауыспалы мән, әрбір пунктке шектеу сәйкес келеді. Кестеде көрсетілген шамалар ауыспалы мәндердің шектеулерге кіретін коэффициентерін нұсқайды. Мысалға, 2

пунктін шектер түрі δ ₁₂ - δ ₂₃ - δ ₂₅ +δ ₃₂ = 0 болады, мұнда (+) белгісі кіретін доғалар алынада, (-) белгісі шығатын доғалар алынада қойылған. Есепті шешу нәтежесінде келесі мәндерді аламыз: δ ₁₂ =δ ₂₃ =δ ₃₄ =δ ₄₅ = 1. Қалған δ _ij = 0 ең қысқа бағдар δ _ij = 1 доғаларды қамтиды. Бұл бағдар 4. 14-суретте көрсетілген. барлық пункттерден өтуіне қарамастан, оның ұзындығы ең аз мәнге

F=2+3+1+2=8. Байқауға болатындай, бір өтпелі пункттен өтетін бағдартар ең ұзын болып келеді. (1-2-5=2+7+9=1-3-5=6+4=10, 1-4-5=8+2=10) .

4. 14-сурет

Практикалық есептерде үлкен бағдарларды байқау қиын, ал мүмкін варианттарды жалпы терудің күрделілігі бар. Сондықтан қысқа жолды жолды табудың бұл тәсілі ең тиімді және қарапайым болып табылады. Жалпы жағдайларда түрлі практикалық есептерді шешуде i-j доғаларға түрлі мағыналарды беруге болады: ұзақтық, құны, еңбек көлемі т. б. Осындай қысқа бағдар таңдау есептері тәріздес деп, ғылыми техникалық мәселелерді шешуде туындайтын түрлі есептерді қабылдауға болады.

Граф теориясының негізгі түсініктері.

Формальдық көзкарас бойынша граф G=(V, E) жиындарының реттелген жұбы, олардың біріншісі төбеле мен түйіндерден тұрады, ал екіншісі - олардың қабырғаларынан. Қабырға екі төбені қосады. Біз графтармен жұмыс істеген кезде, графтың бір төбесінен екінші төбесіне қабырғалардан тұратын жолды қалай жүргізу керектігі жиі қызықтырады. Сондықтан біз қабырға бойымен қозғалысты айтқан кезде, біз АВ қабырғасымен қосылған А төбесінен басқа В төбесіне өті деп түсінеміз. Осы жағдайда біз төбесі В төбесі көрші бір бірімен түйіседі деп айтамыз.

Граф бағдарланған әлде бағдарланбаған болады. Бағдарланбаған графта қабырғаны екі бағытта да өтуге болады. Осы жағдайда қабырға реттелмеген екі төбе, олардың соңы. Егер қабырға соңы дөп келсе, онда қабырға төбені өз-өзімен қосатын тұзақ деп түсініледі. Бағдарланған графта немесе оргафта қабырға екі төбенің қосады: біріншісі оның басы, екіншісі - соңы. Әрі қарай біз қысқарту үшін тек жай қабырға туралы айтамыз, олардың бағдарланғаны әлде бағдарланбағаны мазмұны арқылы түсінікті болады.

Кешірек біз графтарды жиындар арқылы емес жай сурет арқылы көрсетеміз. Төбелер дөңгелектермен, ал қабырғалар сызықтармен бейнеленеді. Дөңгелектер ортасында төбелердің белгісі жазылады. Орграфтың қабырғалары жүруге болатын бағыттарды көрсететін жебелермен белгіленеді.

1. 1 суретінде бағдарланған (а) және бағдарланбаған (б) графтар олардың формалдық сипаттамасымен бірге көрсетілген.

Терминология

Толық граф - бұл әр төбе басқа төбелермен түгел қосылған граф. N төбесі бар толық графтағы қабырғалар саны (N ² -N) /2 тең. Толық бағдарланған графта бір төбеден екінші кез келген төбеге өту рұқсат етіледі. Графта қабырғалар бойынша өту екі бағытта да рұқсат етілгендіктен, ал орграфта тек бір бағытта болғандықтан, толық орграфта қабырға саны екі есе көп немесе олар саны (N ² -N) тең.

Графтың (V _s , E _s ) ішкі графы әлде (V, E) орграфы V _s ⊆V ішкі жиыннан және оларды қосатын қабырғалардың кейбір ішкі жиынан E _s ⊆E тұрады.

Графтағы әлде орграфтағы жол дегеніміз кезекпен өтетін қабырғалар қатары.

Басқаша айтқанда А төбесі В төбесіне дейінгі жол А-дан басталып В төбесіне жеткенге дейінгі қабырғалар тізбегімен өтеді. Формалдық көзқарас бойынша U _i төбесінен U _j төбесіне дейінгі жол бұл графтың U _i U _j +1, U _i+1 U _j+2 …U _j-1 U _j қабырғалар тізбегі. Сонымен қатар, осы жолда кез келген төбе бір реттен артық кездеспеуін талап етемыз. Кез келген жолдың ұзындығы - олардағы қабырғалар саны AB, BC, CD, DE жолының ұзындығы 4-ке тең.

Орграфта әр қабырғаға қабырға салмағы деп аталатын сан бекітілген. Графты бейнелеу барысында қабырға жанына қабырға салмағын жазамыз. Формалды сипаттау кезінде салмақ реттелген әлде реттелмеген төбелер жұбына қосымша элемент болады. Бағдарланған графтармен жұмыс істеген кезде қабырға салмағын онымен өту бағасы деп санаймыз Мысалы, егер P ₁ жолы жалпы салмағы 24 болатын бес қабырғадан тұрса, ал P ₂ жолы - жалпы салмағы 36 болатын үш қабырғадан болса, онда P ₁ жолы қысқалау деп саналады.

Егер кез келген түйін жұбын кем дегенде бір жолмен қосуға болатын болса, онда граф әлде орграф байланысты деп аталады. Цикл дегеніміз бұл бір тқбеден басталатын және осында аяқталатын жол.

Графтарды көрсетудегі мәліметтер құрылымы.

Графтар және орграфтар туралы ақпаратты екі әдіспен сақтауға болады: түйіскен матрицалар түрінде әлде түйісулер тізімі түрінде Бұл параграфта графтар және орграфтар бірдей көрсетілгендіктен, біз олар үшін біз ортақ «граф» терминін қолданамыз. Тағы да біз қолданылатын ақпарат сақтау әдістер графтар мен орграфтарды өңдеу айырмашылықтарын жоятынын көреміз.

Түйісу матрицалары графтың қабырғалары туралы ақпараттарға тез жетуді қамтамасыз етеді. Бірақ, егер графтарда қабырға аз болса, онда матрицаларда толтырылған ұяларға қарағанда бос ұялар көбірек болады. Түйісу тізімінің ұзындығы графтағы қабырғалар санына пропорционалды болады, бірақ тізімді пайдаланған кезде қабырға туралы ақпарат алу уақыты ұзарады.

Бұл әдістердің біреуі де бір-біріне алдын ала артық емес. Керекті әдісті таңдау негізінде, алгоритммен өңделетін граф туралы ақпарат жатады. Егер графта төбелер көп болса, сонымен қатар, олардың әрқайсысы аз ғана төбелер санымен байланыста болса, түйісу тізімі тиімді болады. Себебі ол өте аз орын алады, ал қаралатын қабырғалар тізімі ықшамды. Егер графта төбелер саны аз болса, онда түйісу матрицасын пайдаланған жақсы: ал үлкен болмайды және сиретілген графты матрица түрінде сақтағанда жоғалу мардымсыз болады. Егер графта қабырға көп, ал толықтау болса, онда түйісу матрицасы графта сақтаудың ең жақсы әдісі болады.

Матрица мен түйісу тізімін пайдалану келесі бөлімдерде жан-жақты жазылған.

Түйісу матрицалары.

G= (V, E) Графтың [V] =N төбе саны бар AdyMat түйісу матрицасы NxN көлемді екі өлшемді массив түрінде жазылады. Осы массивтің әр [i, j] ұяшығында 0 мәні жазылады, бұл тек егер U _i төбесінен U _j төбесіне қабырға жүргенде сонда ұяшықта 1 мәні жазылған жағдайлардан басқа сәттерде ғана. Дәлірек айтқанда:

\[\mathrm{AdyM}\bar{\alpha}[t,y]=\frac{\hat{\bf l}\,^{\frac{3}{2}}\tilde{\alpha}\hat{\vec{\alpha}}\tilde{\omega}_{1}\hat{\bf y}\,_{\hat{\bf l}}\ \Xi}{|\cal Q},\hat{\vec{\alpha}}\tilde{\vec{\alpha}}\tilde{\vec{\hat{\alpha}}}\hat{\vec{\hat{\omega}}}{|\cal J}_{\hat{\bf j}}\ \Xi\]

барлық i мен j 1 ден N ге дейін

Орграфтың түйісу матрицасының ұяшығы құрамында шексіз болады, егер сәйкес қабырға жоқ болса, ал қалған басқа жағдайларда оның мәні қабырға салмағын тең. Осындай матрицаның диогональдық элементері 0-ге тең, себебі төбеден өзіне қайтатын сапары ештеңе тұрмайды.

Түйісу тізімі.

[V] =N саны бар G=(V, E) графының Adibist түйісу тізімі ұзындығы N бір өлшемді массив түрінде жазылады. Соның әр элементы тізімге сілтеме түрінде болады. Осындай тізім графтың әр төбесіне бекітілген және ол графтың осы төбесімен көрші әр төбесіне бір-бірден элемент ұстайды.

1. 3 суретінде 1. 1 суретіндегі граф пен орграфтың түйісу тізімін бейнелейді.

2. 1. 1-сурет.

2. 1. Delphi ортасында DLL құруға арналған жаңа проектінің терезесі.

Екі өлшемді экспоненциалды функцияны есептеу үшін Delphi кодты редактордың begin-end аяқтаушы блогының алдына Паскаль тілінде келесі мәтіндік бағдарламаны енгіземіз (2 сур. )

Паскаль тілінде екі өлшемді экспоненциалды функцияны есептеу бағдарламасы.

function ExpFunc2 (x1, x2: Real) : Real; export; stdcall;

var

sum, Func : Real;

i : Byte;

begin

Sum := 0. 0;

for i := 1 To 10 do

begin

Func:= ((Exp(-0. 1*i*x1) - Exp(- 0. 1* i* x2) ) - (Exp(-i) ) ) ;

Sum := Sum + Func* Func;

Result := sum;

end;

exports ExpFunc2;

Бұл бағдарлама x1 және x2 екі формалды параметрі бар: ExpFunec2 функциясын береді. Бұл функцияның бағдарламасының мәтіні Паскаль тіліндегі функцияны хабарлау үшін қолданылатын Function-стандартты операторының көлемімен басталады, онда кейін жақшаның ішіндеформальды параметірлері жазылған ExpFunce2 функциясының аты көрсетіледі. Функцияның атынан кейін екі кілттін сөз жазылады: export-берілген функцияның басқа қосымшаларда да қолданылуы мүмкін екендігін көрсетеді; ctdcfll-аты шақырудың стандартты тәсілін көрсету үшін жазылады. Функция мәтіні айнымалдардың типін хабарлаудан басталады, бұл кезде функция Real айнымалысы типіне сәйкес келетін негізгі мәнән қайтарады. Негізінде екі өлшемді экспоненциялды функция мәнінің есептелінуі x1 және x2 тәуелсіз айнымаларының екі мәні үшін For-To-Do циклінің көлемімен іске асырылады, ол “i” айнымалысы арқылы тізбектеле орындалады. Қарапайым экспоненциалды функцияны есептеу үшін Бір аргументті Exp функциясы қолданылады. Re, sult:=s операторы берілген функцияның қайтымды мәтінін береді. Ақырында, соңғы Export Exp Func2 операторы функцияға басқа қосымшалардан байланысқа шығуға арналған функцияның атын көрсету үшін қызмет етеді. My DLL Delphi. dpr файылдын аты бар мәтіндік бағдарламаның Delphi редакторындағы сыртқы түрі 3-суретте бейнеленген. Delphi редакторында функцияның мәтіндік бағдарламасын жазғаннан кейін проектіні компилициялау және жинақтауды орындау қажет. Бағдарлама мәтініндегі қажетті шығару мақсатында проектіні алдын ала мақсатты түрде компиляцяны орындау керек, ол үшін Delphi редакторының бас мәрізінде келесі операцияны орындаймыз: Project (Проект) /Conpile MyDLL Delphi(Компилировать MyDLL Delphi) . Бұл жағдайда қате бар болса олар көрсетіледі, ал олар туралы ақиғат Delphiедакторының арнайы терезесінде көрініс береді. Жіберілген конпектілерді жойғаннан кейін проектіні жинақтау орындалады, ол үшін Delphi редакторының бас мәзірінде келесі операцияны орындау керек: Projekt (Проект) /Build My DLL Delphi (Создать MyDLL Delphi) . Мұның нәтежесінде берілген проектінің файылдар аты бар бумасында MyDLL Delphi. del атты файл құрылады, ол екі өлшемді экспоненциялды функцияның мәнін есептеуге мүмкіндік беретін орындалушы коды бар файл. Берілген функцияны MS Excel ортасында пайдалану үшін MyDLL Delphi. del файлы MS Windos операциясына жүйесінің жүйелік бумасында көшіріп алу қажет. Мұндай бума ретінде сол дискідегі Windos атты бумадағы System атты буманы алуға болады, ол OC-та орнатылған Осы әрекеттер орнатылғаннан кейін Exp Func2 фукциясы MS Excel бағдарламасының жұмысшы парағындағы ұяшықтарда пайдалануға болатын формулалар түріне ауысады. Бұл жағдайда MS Excel бағдарламасын қосымша баптаудың ешқандай қажеті жоқ. Exp Func2 функциясы берілген кітаптың кез-келген жұмысшы парағының ұяшығынан тікелей шақырылады. Бұл жағдайда MS Excel бағдарламасының ұяшықтарындағы берілген формуланың арнайы шақыру форматын пайдаланған дұрыс. Бұл мақсатта қажетті ұяшықты бөліп алып, функция шеберін шақыру қажет, ол үшін вызвать (шақыру ) функциясын таңдап аламыз. Бұл функция сыртқы кітапханадан функция шақыруға арналған.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.