Рекурсивті функциялар

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Рекурсивті функциялар

Жоспар

Рекурсивті функциялар
Базалық функцияның типтері
алғашқы 0-бойынша тұрғызу, Суперпозиция немесе орнына қою, Рекурсия операторлары.

1. Алгоритмдердің өзі емес, тек олардың бар жоқтығы туралы факті ғана қызықтыратын ғалымдарға алгоритмдерді оқудың мүлде қажеті жоқ. Алгоритм іспеттес бар не жоқ объектілерді тапсақ жеткілікті.

Мұндай объектілер рекурсивті функция делінеді. Мұндай алгоритмдер мен қалай байланысыатынын көрсетелік. W шамасын функция деп, х ₁ , х ₂ , х ₃ шамаларын аргументтер не тәуелсіз айнымалылар деп атаймыз. Егер х ₁ , х ₂ , х ₃ шамаларының нақты мәніне W шамасының анықталған мәні берілетін заң белгілі болса.

Дербес жағдайда функция тек бір ғана аргументке ие болуы мүмкін. Егер функцияның мәнін алуға болатын болса, ондай функцияларды есептелінетін функция деп атайды.

Рекурсивті функция деп - есептелінетін функцияның жеке бір класын айтады. Олардың тапсырмаларының заңы болып табылатын алгоритмдерді біз рекурсивті функцияға сапарлас алгоритмдер деп атаймыз.

Функцияның үш жағын ажырата білу керек:

Функцияның аты (W )
Функциональды жазуы W =f(x1, x2, … xn)
Функцияның мәні.

Мұнда f - функциональды белгі (таңба) .

Базалық функциялардың үш типі:

Тәуелсіз айнымалылардың кез келген мәнінде 0-ге тепе-тең

болатын функциялар . Бұларды

\[{\phi}_{n}\]

-деп белгілейді. Мұндағы n-аргументтер саны. Мысалы: мұндай функциялардың қатарына

\[j_{\mathbf{\tau}_{1}}=y(x);\quad j_{\mathbf{\tau}_{3}}=y(x,y,z)\phi_{n}=y(x_{1},x_{2}...x_{n})\]

функциялары іспеттес функцияларды алуға болады.

Бұл функцияларға байланысты алгоритм былай дейді : Егер

функциональды белгі

\[{\phi}_{n}\]

- түрінде болса, онда берілген функцияға аргументтің мәндерінің жиынтығында 0-қойылады. Мысалы:

\[j_{\mathrm{\bf\Pi}}(0)=0;j_{\mathrm{\bf\Pi}^{2}}(3;4)=0;\mathrm{\bf\Delta}\ \phi_{n}(1,2...66)=0\]

2) Тәуелсіз айнымалылардың кез келген мәнінде тепе-тең функциялар .

Оларды 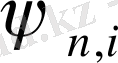деп белгілейміз. Мұндағы n-аргументтер саны; і-аргументтердің бірінің нөмірі, яғни 1

\[{\textsf{E}}i\ \leq n\]

Бұл функцияға байланысты алгоритм былай дейді : Егер функциональды белгі 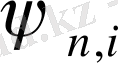- түріне ие болса, онда функция мәні деп - і тәуелсіз айнымалының мәнін аламыз. Мысалы:

\[w=y\ _{3,2}(x,y,z);\quad y\ _{3,2}(2;-4;0)=-4;\quad\quad\psi_{1,1}(5)=5\]

3) Бір тәуелсіз айнымалының ілесу (келесіні алу) функциясы .

Оларды

\[\mathcal{A}\]

функциональды белгісі арқылы белгілейді. Мысалы:

\[l\left(x\right)\lambda\left(z\right)\]

Бұл функцияға байланысты алгоритм былай дейді : Егер

функциональды белгі

\[\mathcal{A}\]

түріне ие болса, онда функция мәні деп - аргументтің мәнінен кейін келетін санды айтамыз. Мысалы:

\[9^{1}=10;l\left(x\right)=x^{1};\ \ \lambda\left(7\right)=8\]

Базалық функциялардың мәні болады, егер олардың аргументтерінің

мәні берілсе.

3. Суперпозиция немесе орнына қою операторы.

Бұл берілген жағдайда екі сөз бір мағынаны береді. Бұл оператор n -

аргументі бар F-функциясынан және f _1, f _{2 . . .} f _n функцияларынан жаңа Ф-функциясын тұрғызады. Ол үшін төменде берілген тепе-теңдік ақиқат болу керек.

\[\varphi\ \:=\:{\cal F}\big(f_{1},f_{2},...,f_{n},\big)\]

Бұл функцияға байланысты алгоритм былай дейді:

«f _1, f _{2 . . .} f _n функцияларының мәнін Ғ-функциясының аргументтерінің мәні деп қабылдап, Ғ-тің мәнін есептеңіздер». Төмендегі: «::=» белгісі анықтама бойынша былай оқылады: Ф функциясын және f _і функциясынан суперпозицияны төмендегідей түрде жазамыз:Ф::=S[F, f ₁ , f ₂ , …, f _n ] . Мұндағы S-суперпозиция белгісі.

Рекурсия операторы

Бұл функция 1-i ^n-1 тәуелсіз айнымалылары бар, 2-сі аталған

айнымалыларға қосымша тағы 2-айнымалысы бар (яғни n+1) екі функция көмегімен n тәуелсіз айнымалылары бар жаңа функция тұрғызады. Рекурсия операторын R әріпімен белгілейміз. Оның қолданылуын төмендегідей түрде жазамыз:

\[\omega:=R[f_{1},f_{2},x,(y)]\]
.

Мұндағы
\[{\mathcal{O}}\]
-жаңадан алынатын функция f ₁ n-1; f ₂ n+1 - тәуелсіз

айнымалысы бар функцияны білдіреді. Х-қосымша аргументтің ішіндегі негізгісі, у-көмекшісі.

Бұл функцияға байланысты алгоритм былай дейді:

«Алынатын жаңа функцияның 0-дік мәндері ретінде n-1 айнымалысы бар функцияның келесі мәндері ретінде f ₂ функциясының мәндерін қарастырамыз»

Алғашқы 0-бойынша тұрғызу операторы.

Кейбір кітаптарда бұл операторды - ең кіші мәнге ұмтылу операторы деп те айтады. Бұл оператор берілген функция бойынша (n+1 аргументі бар) жаңа n-аргументі бар функция тұрғызады. Мұндағы жоғалатын аргумент көмекші аргумент болып табылады. Бұл операторды

\[\mathcal{M}\]

әрпімен белгілейміз. Оның қолданылуын төмендегідей түрде жазамыз.

\[f:=\mu\left[f_{1};\left(x\right)\right]\]

Мұнда х-жоғалатын аргумент.

Бұл операторға байланысты алгоритм былай дейді:

Көмекші аргументке келесі мәндерді бере отырып (0-ден бастап, берілген функция мәні 0-ге айналғанша) функцияны 0-ге айналдыру. Көмекші алгоритмнің алынған мәнін анықталатын функцияның мәні деп қабылдаймыз.

Рекурсивті функциялар деп - базалық функциялар және алғашқы 0-бойынша тұрғызу, рекурсия және суперпозиция операторының көмегімен алынған кез-келген функцияны айтамыз. Егер жоғарыдағы аталғандардың ішінде функциялар алғашқы 0-бойынша тұрғызу операторынсыз алынатын болса, онда ол операторлар - примитивті рекурсивті функциялар деп аталады.

Егер берілген мәндердің кейбірінде шарттар орындалатын болса, онда олар - жалпы рекурсивті функциялар деп аталады.

Черч тезисі.

Теріс емес бүтін мәнді функциялардан алынатын кез-келген есептелетін теріс емес бүтін мәнді функция үшін оған тепе-тең рекурсивті функция бар болып табылады.

Негізгі тезисі.

Бүтін, теріс емес мәндерді өңдейтін (бүтін, теріс емес мәндерге ) кез-келген алгоритм үшін рекурсивті функцияларға сапарлас, берілген алгоритмдерге эквивалентті алгоритм бар болып табылады. Бұл айтылған ойды орыс ғалымдары - Калмагоров пен Успенский толықтырды.

Көп мүшеліктер теориясы

Жоспар:

Көпмүшеліктер теориясы
Кардинал сандар

1. Арифметикаландыру арқасында көптеген математикалық ұғымдар әртүрлі натурал сандар жүйесі арқылы өрнектеледі. Мысалы: кездейсоқ нақты санды шекті натурал сандар жүйесі ретінде қарастыруға болмайды. Оған көз жеткізу үшін П-санын алсақ жетікілкті.

Неміс математигі Г. Кантор ұсынған (1874-1897) көпмүшеліктер теориясы шекті және шексіз заттар жүйесін оқып үйренетін негізгі пән болып табылады. Бұл теорияның негізгі объектісі - жиын. Жиындар құрамына енетін заттар сол жиынның элементтері деп аталады. Жиындар теориясы жиынның элементтеріне қатысты емес қасиеттерін оқып үйретеді. Халық о заманнан әр түрлі нақты және абстракты заттар жиынымен кездесіп келеді. Мысалы: падашшы сиырлармен, құрылысшы үйме құммен, математиктер натурал сандардың қатарларымен жұмыс жасайды.

Заттарды белгілі бір абстракциялау актісі мен байланыстыру біздің сана сезімімізде өздігінен жүреді. Бұл абстракциялаудың екі жағы бар:

Заттар бөлігінің әлсіз әсері(басқа заттарға) не білінеді, не білінбейді және есептелінбейді.
заттар бөлігінің күшті әсері. Заттың толық әсері ретінде қабылданады, сонымен заттар не қосылады, и не орта мәнге келтіріледі. Бұл айтылғандарды анайы мысалмен түсіндіруге болады. Мысалы: Мен кездескен адамды зат ретінде қабылдайтын болсам, онда ол менімен амандасуы мүмкін, не байқамай соғып кетуі мүмкін. Екі боксерді алатын болсақ, олар бір-біріне күш жұмсайды.

Әлсіз әсерге мысал : Ке здескен адамнан тұмау жұғуы мүмкін.

Әлемнің кейбір бөлігі біз үшін абстракция арқасында бір зат болып қабылдануы заттың абстракциялануы деп аталады.
\[a\ \in\!A\]
жазуы а элементінің А жиынында жататындығын білдіреді.

Жиын идеясында Канторға дейін де еңбектер болды. Жиындарды өзара салыстыру әдісін - Кантор ойлап тапты. Оның әдісі бойынша жиындар өзара бір мәнді сәйкестендіру арқылы жүзеге асырылады.

Егер А және В жиындарының арасында өзара бір мәнді сәйкестік орнатуға болатын болса, онда анықтама бойынша мұндай жиындар тең қуатты жиындар деп аталады. Шекті жиындар үшін олардың тең қуаттылығы екі жиынның элемент санының бірдей екендігін білдіреді. Тең қуаттылықты теңдікпен шатастыруға болмайды. Жиындар тең деп аталады , егер біріндегі элемент екіншісінен табылатын болса.

1638 жылы Галилей натурал сандар мен олардың арасындағы бірмәнді сәйкестік орнатуға болатынын анықтады. Егер бір қатарға натурал сандарды, екінші қатарға олардың квадраттарын жазатын болсақ, онда:

1 2 3 4 5 6 7 8 9

1 4 9 16

алуға болады. Галилей мұны Парадокс түрінде бағалады. Онда натурал сандар қанша болса, олардың квадраттарының саны да сонша болады. Екінші жағынан квадраттар саны натурал сандар санынан әлдеқайда аз. Бұдан шығатын факті барлық квадраттар натурал сан болып табылады, ал натурал сандардың барлығы квадрат болмайды. Бұны математикада
\[k\subset N\]

деп белгілейді. К N-ге ішкі жиын болып табылады деген сөз. Мұнда к N-жиынының дұрыс бөлігі деп аталады. Галилей мысалынан Кантор төмендегідей шешім қабылдады. Кейбір жиындар өздерінің дұрыс бөлігімен тең қуатты болуы мүмкін. Бірақ бірде-бір шекті жиын мұндай қасиетке ие емес.

2. Жиындар теориясы сан ұғымына өте қызық толықтырудлар жасауға мүмкіндік береді. Шекті жиынның қуаты деп - оның элементтерін нөмірлеуге қолданылатын ең үлкен натурал санды айтамыз. Тең қуатты, шекті жиындардың қуаты да тең болады.

Теорема : Егер М, қуаты n болатын шекті жиын болатын болса, онда оның (осы жаңа жиындарының элементі болып табылатын) барлық ішкі жиындарының қуаты 2 ⁿ болады. Мысалы: М жиыны а ₁ , а ₂ , а ₃ элементтерінен тұрсын. Демек, жиынның қуаты үшке тең. Оның ішкі жиындары бір элементті: {a ₁ }, {a ₂ }, {a ₃ }

Екі элементті : {a ₁ ; а ₂ }, {a ₁ ; а ₃ }, {a ₂ ; а ₃ }

Үш элементті : {a ₁ ; a ₂ ; а ₃ }

Және бос жиын: {}

Бұлардың саны сезіз. Демек, 8=2 ³

Жиындардың жаңа мінездемесі, оның қуаты бізге санды еске түсіреді. Бұл жағдай бізге кардиналды сан ұғымын енгізуге мүмкіндік береді. М жиынының кардиналды саны деп - оның қуаты m-ді айтамыз. Барлық натурал сандар кардиналды сандарға жатады. Ал барлық кардинал сандар натурал сандарға жата бермейді.

Теорема: Кез келген кардиналды сан м-ге

\[m\ \leq2^{n}\]

теңсіздігі ақиқат. М қуатты жиынның m ¹ қуатты ішкі жиыны

\[m^{1}\ \leq m\]

теңсіздігі қанағаттандырады.

Әріптер, байланыстар, конструкциялар

Жоспар:

1. Әріптер, конструктивті элементтер

2. Әріптер арасындағы әртүрлі орынды байланыстар

Программаларды реттей отырып, біз олар үшін негізгі материал символдар екенін көреміз. Бұл символдардан әлдеқайда күрделі конструкциялар құруға болады. Бұларды « сөздер » деп атайды. Бұл сөздер « командалар » деп аталатын бір жүйеге біріктірілген. Бұйрық деп - құрылымы күрделендірілген команданы айтамыз. Қағаздағы программа деп - бұйрықтардан тұратын программаны айтамыз. Кез-келген программа әріптер, байланыстар және қабықшалардан тұрады. Байланыстар арқылы байланыстырылған объектілерді конструктивті элементтер деп атаймыз.

Не жеке әріп, не қабықшаға алынған конструкция - «конструктивті элемент» деп аталады.
Не бос жиын, не бірнеше конструктивті элементтер «конструктивті элемент» деп аталады.

Әріптер - бұл біз қолданатын символ. Оларды процесс барысында бөліктерге

бөлуге көнбейді.

Байланыстар - бұл конструктивті элементтер арасындағы іс-әрекетті белгілейтін шартты белгілері. « Дала » сөзінде байланыстың үш түрі кездеседі. Бұл сөзде байланыстар ешқандай белгі арқылы берілмеген, бірақ олар бар. Егер белгілер енгізетін болсақ, о→, -о→, →о, онда « Дала » сөзін төмендегіше беруге болады:

о→д-о→а-о→л-о→а→о

Мұндағы:

о→ - бір орынды (бастаушы)

-о→ - екі орынды жалғастырушы

→о - бір орынды аяқтаушы байланыстар.

Бір әріпті сөз төмендегіше беріледі: о→т→о

Әріптердің байланысын білдіретін байланыстан басқа байланыс түрлері де бар. Мысалы, о

\[\longrightarrow\longrightarrow\]

;

Мысалы, «Қоңырау болды» сөзін алсақ,

\[\longrightarrow{\overset{}{\longrightarrow}}\]

( о→қ-о→о-о→ң-о→ы-о→р-о→а-о→у→о) (о→б-о→о-о→л-о→д-о→ы→о) түрінде болады.

Сөздер мен сөйлемдер арасында өте қарапайым бір орынды және екі орынды байланыстар қолданылады. Жалпы жағдайда, байланыс кез-келген конструктивті элементтер санының байланысу қасиетіне ие. Бұл сан «ранг » деп аталады. Төменде берілген суретте 5-рангілі байланыс көрсетілген.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.