Дірілатқарушы механизм динамикасы

Жоспар

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..7

1 Дірілатқарушы механизмнің жұмыс істеу шарты ... ... ... ... ... ... ... ... ... .9

2.1 Дірілатқарушы механизміді кинематикалық зерттеу ... ... ... ... ... ... ..11
2.2 Беріліс қатынастар теңдеуін құру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..20
2.3 Звенолардың ауырлық центірі мен удеулері жән жылдамдықтары ... .22

3.1Тербелмелі конвейр звеноларының келтірілген деференциалдық теңдеуін құру және шешу ... ... 27
3.2 Звенолардың келтірілген инерция моменті ... ... ... ... ... ... ... ... ... ... .29

4 Дірілатқарушы конвейр теңдеуін жуықтап шешу әдісі ... ... ... ... ... ... .33
5 Сандық шешімдер және нәтижелерді өңдеу ... ... ... ... ... ... ... ... ... ... ...37

Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 39
Пайдаланған әдебиеттер тізімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .40

А Қосымша ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 41
Б Қосымша ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 48

Пән: Автоматтандыру, Техника
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 41 бет
Таңдаулыға:

ҚАЗАҚСТАН рЕСПУБЛИКАСЫНЫҢ бІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
қ.И. Сәтбаев атындағы қазақ ұлттық техникалық университеті
Машинажасау институты
Қолданбалы және теориялық механика кафедрасы

Қорғауға рұқсат берілді
Кафедра меңгерушісі тех. ғылым.
докторы

С.М. Ибраев
__________ 2007г.

ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы Дірілатқарушы механизм динамикасы

птікір беруші: Жетекші:
техн.ғылым.кандидаты, доцент
техн.ғылым.кандидаты,доцент _________________ Н.К. Джамалов
_______________С.Б. Косболов
________________2007г.
________________2007г.

Стандарт бойынша кеңесші:
Оқытушы Студент
Иманбердиев М.Ж.
_____________ Е.Т. Бекенов
Мамандығы 250240
_______________2007г. Тобы ДиПМ-
02-1қ

АЛМАТЫ 2007

Қаныш Сәтбаев атындағы Қазақ ұлттық техникалық университеті

Машина жасау институты
Мамандығы 250240- Машиналар динамикасы және беріктігі
Кафедра Теориялық және қолданбалы механика

Диплом жұмысын орындауға
ТАПСЫРМА
Студетке

Жұмыстың такырыбы Дірілатқарушы механизм динамикасы. Жоғарғы
оқу орны бойынша ________ _________№____
Бұйрықпен бекітілген
Аяқталған жұмысты тапсыру мерзімі 30 сәуір 2007
Жұмыстың негізгі деректері :
1. Кріспе. Дірілатқарушы механизмнің жұмыс істеу шарттарын енгізу.
2. Дірілатқарушы механизм кинематикалық есебін құру.
3. Тербелмелі конвейр звеноларының деференциалдық теңдеуін шешу.
4. Дірілатқарушы конвейр теңдеуін шешудің тйімді әдістерін қарастыру.
5. ”Visual Basic” программасы көмегімен кедергі және қозғаушы
күштерінің графигін тұрғызу
Диплом жұмысында зерттелетің мәселелердің тізімі немесе диплом
жұмысының қысқаша мазмұны:
Берілген заңдылықты орындайтын алты звенолы үшінші класты механизмдерінің
кинематикалық және динамикалық зерттеу.

График материалдарының тізімі (міндетті сызбалардың дәл
көрсетілуімен)
Жобаланған діріл атқарушы механизмнің кекіні және шешімін графиктік түрде
тұрғызу және таңдау.

Ұсынылатың негізгі әдебиет
1. И.И.Артоболевский, Теория механизмов и машин, 1992 г., М.: Наука.
2. А.И. Левитский, Теория механизмов и машин, 1990 г., М.: Наука.
3. А.И. Левитский, О.Н. Левитская, Курс по теории механизмов и машин,
1986 г., М.: Наука.
4. Под редакцией К.В. Фролова, Теория механизмов и машин, 1992г., М.:
Наука.

Диплом жұмысы дайндау кестесі

№ Тараулардың аттары,зерттелетін Жетекшіге ұсыну Ескерту
мәселелердің тізімі мерзімі
1 Кріспе. Дірілатқарушы
механизмнің жұмыс істеу
шарттарын енгізу. 20.03.07
2 Дірілатқарушы механизм
кинематикалық есебін құру 30.03.07
3 Тербелмелі конвейр звеноларының
деференциалдық теңдеуін шешу.
10.04.07
4 Дірілатқарушы конвейр теңдеуін
шешудің тйімді әдістерін 20.04.07
қарастыру.
5 ”Visual Basic” программасы
көмегімен кедергі және қозғаушы1.05.07
күштерінің графигін тұрғызу

Тапсырма берілген күні 4 қаңтар 2007

Кафедра меңгерушісі
С.М. Ибраев

Жұмыс жетекшісі
С.Б. Косболов

Тапсырманы орындауға қабылдады студент Иманбердиев
М.Ж.

Аңдатпа

Осы жұмыста құймалы өндірістің балқыту пештерінің шахтасындағы
жүктемені қажетті етіп бөліп пешкіге салып отыратын, алты звенолы үшінші
классты дірілатқарушы механизмді кинематикалық және динамикалық зерттеу
мәселелері қарастырылған.
Механизмді кинематикалық зерттеуде, звенолардың қозғалыс орны мен
жылдамдықтары, жетекші звеноның қозғалыс орны мен жылдамдығына байланысты
анықтау фунциялары алынды.
Механизм звенолар қозғалысының келтірілген деференциалдық теңдеуі
алынды. Механизм қозғалыс теңдеуін ЭВМ-да қозғаушы күштер мен кедергі
күшінің түрлі мәндерінде Visual Basic алгоритмдік тіл көмегімен шешілді.
Жетекші звеноның бұрыштық жылдамдықтарының өзгеру графиктерін талдау
кезінде келесі қорытынды жасауға болады.
Мұнда нәтижелер кестесі мен орынаустыру графиктері және жетекші звено
жылдамдығының уақытқа тәуелділігі келтірілген. Қозғалыс теңдеуі
дірілатқарушы конвейрдің келтірілген моменттері мен кедергі күшінің түрлі
моменттері кезінде шешіледі, жуықталған шешім ЭЕМ-да Visual Basic
алгоритмдік программасы көмегімен жүзеге асырылды.

Аннотация

Существующие методы анализа и синтеза указанных механизмов из-за трудностей
или невозможность алгоритмизации всех этапов исследования не могут служить
основой для создания программ. В связи с этим является актуальной задача
разработки анализа и синтеза сложных механизмов с заданными законами
движения выходного и входного звеньев.
Существующие методы синтеза не позволяют автоматизировать в полной
мере все этапы структурно-кинематического синтеза и указать все мыслимые
структурные схемы сложных механизмов с заданными законами входного и
выходного звеньев. Рассмотрены основные направления в создании
автоматизированных систем проектировании новых механизмов и машин и
отмечена необходимость разработки машинных методов синтеза новых механизмов
и машин.
На основе задания плоскопараллельного движения двух подвижных
плоскостей относительно неподвижной плоскости сформулированы математические
задачи синтеза четырехзвенных исходных кинематических цепей (ИКЦ) с
вращательными и с поступательными парами, имеющих три степени свободы и
семь неизвестных параметров.
Разработан общий метод синтеза плоских рычажных механизмов по заданным
законам движения входного и выходного звеньев. В основе предлагаемого
метода лежит возможность составления структурной схемы любого плоского
механизма из исходной кинематической цепи (ИКЦ) и ее модификации. Последнее
позволяет весьма просто составлять структурную схему и целевую функцию
синтеза механизма с помощью ЭВМ.
Синтез исходной кинематической цепи (ИКЦ) и ее модификации в
зависимости от заданных условий синтеза может привести к непосредственному
синтезу механизма.

МАЗМҰНЫ

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... ... ... ... ... 7
1 Дірілатқарушы механизмнің жұмыс істеу
шарты ... ... ... ... ... ... ... .. ... ...9
2.1 Дірілатқарушы механизміді кинематикалық
зерттеу ... ... ... ... ... ... ..11
2.2 Беріліс қатынастар теңдеуін
құру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...20
2.3 Звенолардың ауырлық центірі мен удеулері жән
жылдамдықтары ... ... ... ... ... .. ... ... ... ... ... ... ... ... .
... ... ... ... ... ... ... ... ... .22
3.1Тербелмелі конвейр звеноларының келтірілген деференциалдық
теңдеуін құру және
шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ...27
3.2 Звенолардың келтірілген инерция
моменті ... ... ... ... ... ... ... ... ... ... .29
4 Дірілатқарушы конвейр теңдеуін жуықтап шешу
әдісі ... ... ... ... ... ... .33
5 Сандық шешімдер және нәтижелерді
өңдеу ... ... ... ... ... ... ... .. ... ... ... .37
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... ... ... 39
Пайдаланған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... .4
0
А
Қосымша ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... 41
Б
Қосымша ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... 48

КІРІСПЕ

Түрлі өнерістерде ыстық, улы химиялық агресивті жүктерді тасымалдау
үшін, олардың орын ауыстыруының толық геометриялылығын қамтамасыз ету
кезінде, сондай-ақ эмульсия майымен, құймалы қалыптан, құймалы шихтадан
және тағы басқа, ұсақталған ыстық жүктеме, суланған және метал жанқасын
тасуға арналған тербелмелі конвейрлер кең қолданады.
Тербелмелі конвейр қозғалмайтын рама ілінген немесе жапсырылған науа
болып табылады. Науа тербелмелі қозғалыстар жасайды, нәтежесінде науадағы
жүк, науаға қатысты орын ауыстырады. Қозғалыс сипаты және оның
параметірлері науамен жасалатын тербеліс сипаттамасымен анықталады.
Тербелмелі конвейлер науаның қозғалу кезінде, жүк қозғалысының сипаты
бойынша инерциялық болып бөлінеді, онда инерция күш әсерінен жүк науа
бойымен сырғйды және дірілдемелі (выбрационый) болып бөлінеді, онда жүк
науадан үзіледі және науа бойымен ұсақ орын ауыстырады. Көптеген
артықшылықтарына байланысты соңғы уақытта дірілатқарушы конвейрлер кең
қолданыс тапты.
Осы жұмыста құймалы өндірістің балқыту пештерінің шахтасындағы
жүктемені қажетті етіп, бөліп пешкіге салып отыратын дірілатқарушы
механизмді кинематикалық және динамикалық зерттеу мәселелері туындайды.
Бұл дипломдыық жобаны тақырыбы бойынша негізгі 5-бөлімде
қарастырылды.
1-ші бөлімде дірілатқарушы ковейрдің жұмыс істеу шарттары
сипатталады.
2-ші бөлім механизмді кинематикалық зерттеуге арналған.
3-ші бөлімд дірілатқарушы конвейр қозғалыс звеноларының келтірілген
деференциалдық теңдеуін құру.
4-ші бөлім дірілатқарушы конвейр қозғалысының теңдеуін шешудің
жуықталған әдісі келтірген.
5-ші бөлімде Конвейр қозғалыс теңдеуінің шешімін талдауға арналған.
Мұнда нәтижелер кестесі мен орынаустыру графиктері және жетекші звено
жылдамдығының уақытқа тәуелділігі келтірілген. Қозғалыс теңдеуі
дірілатқарушы конвейрдің келтірілген моменттері мен кедергі күшінің түрлі
моменттері кезінде шешіледі, жуықталған шешім ЭЕМ-да Visual Basic
алгоритмдік программасы көмегімен жүзеге асырылды.

1 Тербелмелі дірілатқарушы механизмнің жұмыс істеу шарты

Дірілатқарушы алты звенолы механизм. Мұнда 1-айналшақ, 2,3-арқалық
звенолар, 4,5 күйенте 2.1 суретте. Тіреулер серпімді орналасқандықтан жүкті
науа алға қарай қозғалғанда аз ғана көтеріледі, ал артқа қозғалғанда
төменге түседі. Айналшақ радиусы шатун және трек стержень ұзындығымен
салыстырғанда аз алынады, нәтижеде науа жылдамдығының өзгеру заңы νн
синусойдалыққа жақын, ал науа қозғалысының өзін тіректі сырыққа нормаль
бойынша бағытталған түзу сызықты етіп қарастыруға болады.
Науа үдеуі: ан
Тік: ан.у
және көлденең: ан.х
Құраушының геометриялық қосындысы ретінде алуға болады. Науа ілгері
жүргенде тік үдеу құраушысы жоғары бағытталды. Бұл кезде салмағы G жүк
бөлшегіне тік
mан.у,

және көлденең
mан.х,
Инерция күш құраушылары және науа бойымен оның қозғалыс жағына
бғытталған үйкеліс күші әсер етеді.
Жүк бөлшектері науаның тура жүрісінің баяулау кезінде де (науа
жылдамдығының өзгеру графигіндегі АВ аумағы ) ілгері орын ауыстыру үшін,
үйкеліс күші, инерциялық күштің көлденең құраушысынан үлкен болуы қажет,
яғни
f [ m(g + ан.у) ] mjн.х,
(1)

мұндағы f - үйкеліс коэфицент.

1.1 сурет

ан.х = ан.cosα
(2)

және
ан.у = ан. sinα
(3)

Онда жүктің науадан бөлек ілгері орын ауыстыруын қамтамасыз ету
шарты мына түрге ие болады.
ан fg cos α - f sin α
(4)
Науа төмен түскендегі кері жүрісінде инерциялық күштің тік құраушысы
жүктің науаға түсіретін қысымы мен жүк пен науа арасындағы үйкеліс күшін
fн - ді азайта отырып жоғары қарай бағытталады. Бөлшек өзінің ілгері
қозғалысын жалғастыру үшін және науаның кері жүрісі кезінде инерциялық
күштің көлденең құраушысы кері жүріс кезінде үйкеліс күшінен көп болу
қажет, яғни
mа fm (g - а)
(5)
Жүктің науа бойынша қозғалысы, науа қозғалысының барлық сатыларында
жүктің науадан үзілуге болмайтынын орындауы кажет. Ол үшін жүктің науаға
қысымы әрқашан нөлден үлкен болу, шарты орындалуы қажет. Яғни
m( g - аж.у ) o
(6)
Немесе
а н.у g
(7)
Яғни науа үдеуінің тік құраушысы әрқашан ауырлық үдеуінен кіші болуы
қажет.

2.1 Дірілатқарушы механизм кинематикасы

2.1-суретте өндіріс шахтасында құю пешіне жүктемені мөлшерлеп салып
отыратын ВНИТАРМАТУРА-да жобаланатын дірілатқарушы механизм сүлбесі
көрсетілген. Бұл механизм 3-класты ВЕД звено ҒЕ, АВ, GД-3 бөлігі бар
базистік болып табылады. ОА звеносы – жетекші звено [1].
Бұл механизмнің қозғалыс дәрежесі W=1 тең, сондықтан келтірілген
звенолар және механизм нүктелерінің орын ауыстыру жылдамдықтары және үдеу
функциалары болып табылалы. Сондықтан келтірілгнен звенолар мен жетекші
звенолар аралығындағы аналитикалық тәуелділіктерден, звенолардың
жылдамдықтары мен орын аустыруын, табамыз.
Механизм келесі сипаттамаға ие:
2.1 кесте - Звенолар
1 2 3 4 5
масса
кг. m 1=30 m 2=65 m 3=1160 m 4=59 m 5=59
Ұзындық l 1=6 l 2=430 l 3=1700 l 4=1440 l 5=1440
мм.

Жетекші звено тірегі бар айналмалы жұпқа енетіндіктен:
φ1 = φ1 (t)
Фунциясы мен белгілейміз, мұндағы φ1 - жетекші звеноның тірекпен
байланысты қозғалмайтын ХОУ координат жүйесіне қатысты айналу бұрышы,
t-уақыт .
Енді келтірілген звеноның орын ауыстыруымен жылдамдықтарын табу үшін
тұйықталған векторлық контурлар әдісін қолданамыз

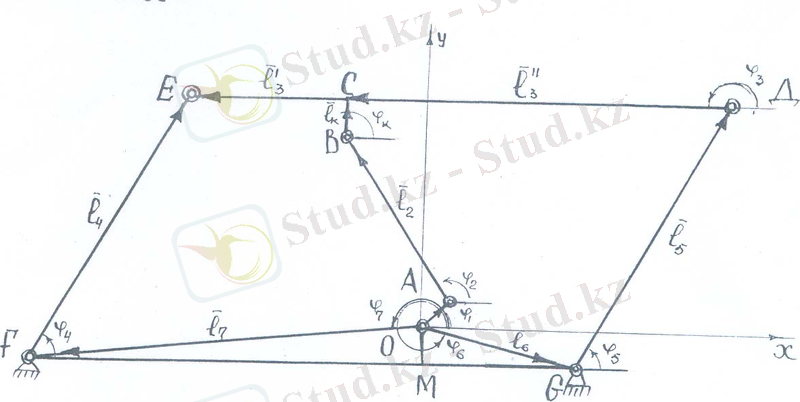
2.1 сурет

Бірінші контур ОАВСЕҒО және екіншісі ОАВСДGО. Бұл тұйық контурларды
векторлық түрде жазамыз және Х және У остеріне проекциалаймыз.
Бірінші контур:
l1 + l2 + lк + =
l7 + l4
Екінші контур:
l1 + l2 + lк + = l6 +
l5 +

(2.1)

(2.2)

ЕД звеносы әр қашан көлденең бағытта қозғалғандықтан φ3 = 1800
өзгермейді. Есептің шарты бойынша звенолар: l4 = l5 , φ4 = φ5, φх =
900. Сондықтан былай теңестіріп аламыз:

(2.3)

(2.4)

Теңдеулер (2.3) және (2.4) теңестіргенде, теңдіктің оң жақтары тең
болғандықтан, орындарын ауыстыруға болады . Осыдан шығатыны оң жағы тең
болуы керек.
Осы теңдікті көрсетеміз:

Шамалары l1 sin φ1 және lк, қысқартқаннан кейін мына
теңдікті аламыз:

(2.5)

Звенолар l7, l6, , ұзындықтарын табамыз және φ6, φ7
бұрышын:
φ7 бұрышын табу үшін ∆MFO қарастырымыз:

α = 10 40’
Бұрышымыз φ7 мынаған тең φ7 = 1800 + 10 40’ = 1810 40’
Бұрышын φ6, ∆МGO -дан табамыз:

β = arctg 0,1066 = 60
β = 60 то φ6 = 3600 – 60 = 3540 болса,
Бұрыштарымыз φ6= 3540 және φ7 = 1810 40’тең болады.
Ұзындықтарды l7, l6, , сызбадан табамыз. Сызба
бойынша олар мынаған тең: [3]

l7 = 1325,6 мм
l6 = 377,1 мм
l3 = 1058 мм
l3 = 642 мм

Табылған барша ұзындықтарды (2.5) жүйеге қоямыз:

1325,6 (- cos 10 40’) + 642 = 377,1 cos 60 – 1058 – 683,1 ≈ - 683
l7 sin φ7 = l6 sin φ6
1325,6 ( - 0,03) = 377,1 (- sin 60)
- 39 ≈ - 39

Біз мұндағы екі жүйе өзара тең екенін дәлелдедік, осыған байланысты
осы төрт тендіктен екі теңдеуді қарастыруға болады.

(2.6)

Теңдеу (2.6) шешу үшін φ2 және φ4, бұрышын φ1 бұрышына қатысты
табамыз.
Ол үшін А және В жүйесінің оң жағын белгілейміз, олардың ұзындықтары
бізге белгілі:

А = l7 cos φ7 - l1 cos φ1 + l3
В = l7 sin φ7 - l1 sin φ1 - lx

Осыдан екі белгісізі бар екі теңдеу аламыз:

(2.7)

Белгі А және В φ1 бұрышына қатысты
А (φ1) , В (φ1)
Екінші теңдіктен sin φ2 табамыз:

(2.7’)

Шама sin φ2 мына түрде өрнектейміз:

Өрнекті (2.7’) теңдікке қоямыз:

(2.7”)
Теңдеу (2.7”) квадраттық теңдеуге айналдырымыз:

осыдан cosφ2 табамыз:

Енді cosφ2 (2.7) теңдеуіне қоямыз

Өректі квадраттаймыз:

Енді теңдіктің екі жағын көбейтеміз :

Шамалады С –деп белгілейміз:

Белгі С жалпыланған координата φ1 , қатысты С = С (φ1) фунциясы
болады:
Осыдан шығатыны:

Өрнекті квадыраттаймыз:

Шама sin2 φ4 және sin φ4 жақшаға аламыз,

(А )

Белгілеулер енгіземіз:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.