Граф тиімділік есептерін шешу әдістерінің алгоритмдері мен программалары

Жоспар

Кіріспе

I . ТАРАУ Граф теориясының негізгі түсініктері
1.1. Графтағы алгоритмдер
1.2. Графты көрсетудегі мәліметтер құрылымы
1.3. Графикалық торлар

II . ТАРАУ Borland Delphi ортасында сыртқы функциялар құру және оны
MS Excel ортасында қолдану
2.1. Delphi ортасында DLL құруға арналған жаңа проектінің терезесі
2.2. MS Excel көмегімен бағытталған графика минималды жол туралы есепті шешу
2.3. Дискретті және комбинаторлық тиімділеу есебі
2.4. Дейкстер белгілеу алгоритмі көмегімен графта минимальды жол туралы есепті шешу

Қортынды
Пайдаланған әдебиеттер тізімі

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:

Қазақстан Республикасы Білім және Ғылым Министрлігі
Қазақ мемлекеттік қыздар педагогика институты

Жаратылыстану факультеті

Информатика кафедрасы

Тақырыбы: Граф тиімділік есептерін шешу әдістерінің алгоритмдері мен
программалары

Диплом жұмысы Орындаған: Муса.А.О.
Кафедра мәжілісінде талқыланып, 010540 информатика
қорғауға жіберілді мамандығының 4-
курс студенті
Хаттама № _____ _________2006 ж Ғылыми жетекшісі: аға оқытушы
Кафедра меңгерушісі Ж.И. Ахатова
_________ Г.И.Салғараева

Алматы 2006

Мазмұны

Кіріспе ___________________________________ _______________________

I – ТАРАУ Граф теориясының негізгі түсініктері

1.1. Графтағы алгоритмдер ___________________________________ _____

1.2. Графты көрсетудегі мәліметтер құрылымы_______________________

1.3. Графикалық торлар___________________________________ ________

II - ТАРАУ Borland Delphi ортасында сыртқы функциялар құру және оны
MS Excel ортасында
қолдану____________________________ ____

2.1. Delphi ортасында DLL құруға арналған жаңа проектінің терезесі
___________________________________ __________________________
2.2. MS Excel көмегімен бағытталған графика минималды жол
туралы есепті шешу___________________________________ _______

2.3. Дискретті және комбинаторлық тиімділеу есебі__________________

2.4. Дейкстер белгілеу алгоритмі көмегімен графта минимальды жол
туралы есепті шешу___________________________________ _______

Қортынды

Пайдаланған әдебиеттер тізімі

Қосымша

КІРІСПЕ

Ғылыми жұмыс, зерттеу дегеніміз-адамның енбектену іс - әрекетерінің
ерекше түрі. Бұл іс-әрекет адамнан еңбекқорлық, мақсаттану, туандаған
сәтсіздікті жене білу қабілетін, оның интелектуальды мүмкіндіктеріне
барынша пайдалунуды қажет етеді. Ғылыми еңбктін мақсаты адамзатқа осы
уақытқа дейін беймәлім ақиқатты ашу, табиғат жұмбақтарына тенерірек үнілу,
адамзат игелігіне пайдаланатын табиғи күштерді қолданудың жаңа жолдарын,
адамды, оны ішкі, яғни деңе күштерін және рухани қайратын зерттеу. Ғылым
аясында еңбек ету әрқашанда құрметті және мәртебелі болып саналады. өздерін
ғылымға арнаған адамзат баласының ен жақсы өкілдерінің есімдері халық
жүрегінде мәнгі сақталуында.
Ғылымда бір нәрсе жасау үшін жас ғылым сол салада терең білімге,
еңбекқорлыққа ие болу керек, өз таңым іс - әрекеттерінде қомақты нәтижеге
жету үшін басқа да қажетті талаптарға сай болу керек.
Ғылыми заңдарға байланыс жасалған гипотезалардың бірнеше түрі
болады. Олар эприкалық, теориялық, құрылмдық, статикалық, динамикалық,
санды және сапалы болып бөлінеді.
Ықтималдық сипатына қарамастан статика болжамы өз құңдылығын
төмендетпейді. Бұл болжамдардың толықтығын немесе шынайлығы немесе
динамика заңдары негізінде жасалған болжамдардан кем емес.
Саңды заңдар, математикалық формуламен теңдіктер тілінде
тұжұрымдалады. Формальды математика аппаратты қолданған саңды заңдар
болжаманаң жоғары дәлдігіне жетуге мүмкіңдік береді.
Қазіргі уақытта ғылыми техниканың дамуы жоғары деңгейге жетті,
өңдіріс көлемі жылдан жылға өсіп келеді, адам іс - әрекетті қоршаған
ортаға зор ықпал жасауда, соңдықтан оның қабылдаған шешіміне болашақ
өмір тәуелді мойындау керек. Әрбір техника жаңашылдығын іске асыру
барысында көптеген халыққа әсері тиіп, адам тағдырын өзгертуге әкеліп
соғады. Мұндай жағдайда шешім қабылдауда дұрыс, ғылыми негізделген
ұсыныстарға сүйену аса қажет болып саналады.
Жоғары деңгейлі тілдер адамның көру-есту (аудио-видио) сезімімен
қабылдануына ыңғайлы.
Жоғары деңгейлі тілдер үлкен ұйымдар арқылы (мысалға, ANSI (Америка
ұлттық стандарттар институты)) стандартқа келтрілген. Мұндай
стандарттау, тілдерді бір – бірне тасымалдауды жеңілдетеді. Жоғары
деңгейлі тілдер қатарына FORTRAN, COBOL, PASCAL және т.б. жатады.
Қазіргі күнде компьютер әлемінде бағдарламалау тілдерінің саң алуан
түрлері бар. Нақтылы амалды жасайтын бағдарламаны түрлі тілде жазуға
болады: Visual Basic-VBA, Delphi 7, C++.
Visual Basic-VBA бағдарламалау тілін және орта ретінде пайдалануға
(Visual Basic-VBA) Microsoft жүйесіне еңген Word, Excel, Power Point
немсе Access қосымшалар арқылы қолданылады.
PASCAL бағдарламалау тілі сәтт болғаны соңдай, оның пайда
болуынан бастап қысқа мерзім ішінде түрлі фирмалар сан алуан
компилятор жасап үлгерді. Солардың ішінде ең тиімдісі болып Borland
американдық фирмасы жасаған мәтн редакторы мен жоғары нәтижелі
компилятор қосылған Turbo PASCAL жүйесі есептелінеді. Мұнда
қолданылатын бағдарламалау тілі де осы есімге ие болды.
Есептегіш техника мен бағдарламалау техналогиясының дамуы жаңа
бағдарлама өнімдерінің пайда болуына әкеледі. Осы Borland фирмасы
жасаған Delphi деп аталатын өнім Windows ұстанымында жұмыс істеуге
бағытталған бағдарламалар жасау ортасы.
Бағдарламаны Delphi ортасында ұсыну үшін негізгі айқын Turbo PASCAL
тілімен саласы Borland фирмасы жасаған Object Pacal тілін
пайдаланады. “Object” деген сөз бұл тілі объектте бағытталған
бағдарламалау концепцияын қолдайтынына ерекше назар аударады.
Негізгі диплом жұмысымда қарастырғаным MS Excel – де қолданылатын ең
минимальді жолды табатын фугкцияны Borland Delphi – де жасауы.
Мысал ретнде қарастырғаным Borland Delphi 7 ортасында жасалып MS
Excel ортасында сәйкес қолданылатын бағытталған графтағы минимальды
жолды табатын функцияны қарастырдым, сонымен қатар Visual Basic-VBA
ортасында да қарастырылған мысал келтірілген.

1.1. Граф теориясының негізгі түсініктері

Формальдық көзкарас бойынша граф G=(V,E) жиындарының реттелген жұбы,
олардың біріншісі төбеле мен түйіндерден тұрады, ал екіншісі – олардың
қабырғаларынан. Қабырға екі төбені қосады. Біз графтармен жұмыс істеген
кезде, графтың бір төбесінен екінші төбесіне қабырғалардан тұратын жолды
қалай жүргізу керектігі жиі қызықтырады. Сондықтан біз қабырға бойымен
қозғалысты айтқан кезде, біз АВ қабырғасымен қосылған А төбесінен басқа В
төбесіне өті деп түсінеміз. Осы жағдайда біз төбесі В төбесі көрші бір
бірімен түйіседі деп айтамыз.
Граф бағдарланған әлде бағдарланбаған болады. Бағдарланбаған графта
қабырғаны екі бағытта да өтуге болады. Осы жағдайда қабырға реттелмеген екі
төбе, олардың соңы. Егер қабырға соңы дөп келсе, онда қабырға төбені өз-
өзімен қосатын тұзақ деп түсініледі. Бағдарланған графта немесе орграфта
қабырға екі төбені қосады: біріншісі оның басы, екіншісі – соңы. Әрі қарай
біз қысқарту үшін тек жай қабырға туралы айтамыз, олардың бағдарланғаны
әлде бағдарланбағаны мазмұны арқылы түсінікті болады.
Кешірек біз графтарды жиындар арқылы емес жай сурет арқылы
көрсетеміз. Төбелер дөңгелектермен, ал қабырғалар сызықтармен бейнеленеді.
Дөңгелектер ортасында төбелердің белгісі жазылады. Орграфтың қабырғалары
жүруге болатын бағыттарды көрсететін жебелермен белгіленеді.
1 суретінде бағдарланған (а) және бағдарланбаған (б) графтар олардың
формалдық сипаттамасымен бірге көрсетілген.

Терминология

Толық граф – бұл әр төбе басқа төбелермен түгел қосылған граф. N
төбесі бар толық графтағы қабырғалар саны (тұзақсыз)
(N2-N)2 тең. Толық бағдарланған графта бір төбеден екінші кез келген
төбеге өту рұқсат етіледі. Графта қабырғалар бойынша өту екі бағытта да
рұқсат етілгендіктен, ал орграфта тек бір бағытта болғандықтан, толық
орграфта қабырға саны екі есе көп немесе олар саны (N2-N)тең.
Графтың (Vs, Es) ішкі графы әлде (V, E) орграфы Vs(V ішкі жиыннан
және оларды қосатын қабырғалардың кейбір ішкі жиынан Es(E тұрады.
Графтағы әлде орграфтағы жол дегеніміз кезекпен өтетін қабырғалар
қатары.
Басқаша айтқанда А төбесі В төбесіне дейінгі жол А-дан басталып В
төбесіне жеткенге дейінгі қабырғалар тізбегімен өтеді. Формалдық көзқарас
бойынша Ui төбесінен Uj төбесіне дейінгі жол бұл графтың UiUj+1, Ui+1Uj+2
...Uj-1Uj қабырғалар тізбегі. Сонымен қатар, осы жолда кез келген төбе бір
реттен артық кездеспеуін талап етемыз. Кез келген жолдың ұзындығы –
олардағы қабырғалар саны AB, BC, CD, DE жолының ұзындығы 4-ке тең.
Көтеріңкі графта әлде орграфта әр қабырғаға қабырға салмағы деп
аталатын сан бекітілген. Графты бейнелеу барысында қабырға жанына қабырға
салмағын жазамыз. Формалды сипаттау кезінде салмақ реттелген әлде
реттелмеген төбелер жұбына қосымша элемент болады. Бағдарланған графтармен
жұмыс істеген кезде қабырға салмағын онымен өту бағасы деп санаймыз.
Көтеріңкі графта жол құны бүкіл жолдағы қабырғалар салмағының қосындысына
тең. Көтеріңкі графтағы ең төте жол – қабырғалар салмағы ең төмен жол,
тіпті жолдағы қабырғалар сан азайса да. Мысалы, егер P1 жолы жалпы салмағы
24 болатын бес қабырғадан тұрса, ал P2 жолы – жалпы салмағы 36 болатын үш
қабырғадан болса, онда P1 жолы қысқалау деп саналады.
Егер кез келген түйін жұбын кем дегенде бір жолмен қосуға болатын
болса, онда граф әлде орграф байланысты деп аталады. Цикл дегеніміз бұл бір
тқбеден басталатын және осында аяқталатын жол. Ациклдік графта әлде
орграфта циклдар жоқ. Байланысшы ациклдік граф шежіре деп аталады.
Түбірленбеген граф құрылымы шежірелік сияқты, тек онда түбір бөлінбеген.
Бірақ түбірленбеген шежіренің әр төбесі оның түбірі қызметін атқара алады.

1.2. Графтағы алгоритмдер

Графтар формальды түрде көп бір-біріне жуық жағдайларды баяндайды. Ең
үйреншікті мысал болып қиылыстар мен оларды байланыстыратын жолдар
көрсетілген автожолдар картасы болып табылады. Қиылыстар графтардың
төбелері болса, ал жолдар олардың қабырғалары. Кейде ол графтар бағытталған
(біржақты өозғалысты көшеге ұқсас) әлде салмақталған - әр жолда жүру ақысы
көрсетілген (егер, мысалы, жолдар ақылы болса). Біз графлар тілін әрі қарай
жете зерттелген сайын, графтардың жол картасына ұқсастығы тереңдей түседі.

Графтардың математикалық аспектісін меңгергеннен кейін, біз олардың
компьютер зердесі құрамында болуын және оларды өңдеу алгоритмдерімен
айналысамыз. Біз бір бірінен артық шығымдар көлемі бойынша айырмашылығы бар
графтарды сақтау әдістерінің көп екенін көреміз, ал әдісті таңдау графтың
өзіне байланысты.
Кейде кейбір ақпаратты көп адамдар топтарына әлде үлкен желідегі
барлық компьютерлерге таратуға тура келеді. Біз ақпараттың топтық әр
мүшщесіне жеткенін қалаймыз, бірақ сонымен қатар тек бір рет қана. Осы
мақсатта кейбір топтарда “телефондық шежіре” ұйымдастырылады: бұл жағдайда
тың жаңалық алған топ мүшесі, оны қатысушылардың аз мөлшеріне хабарлайды.
Егер шежіреде топтың әр мүшесі бір рет ғана кездессе, онда шежіре биіктігі
үлкен емес және ақпарат барлығына тез жетеді. Ал жалпы көріністі графларда
жағдай күрделірек, себебі орталау графтарда шежіреге қарағанда байланыс
әлдеқайда көбірек. Осы қиындықты шешу мақсатында біз графтарды аралаудың
екі әдісін үйренеміз: тереңдікке және деңгейлер бойынша.
Діңгекті шежіре – циклдары жоқ, құрамында графтың кейбір қабырғалары
мен бүкіл төбелері бар байланысты ішкі жиынды граф болып табылады.
Минималдық діңгекті шежіре дегеніміз қабырғалар мөлшері бар діңгекті
шежіре. Минималдық діңгекті шежірені қолданудың бір саласы ішкі компьютер
желісін ұймыдастыру. Байланыстыру бекеттері (станциялары) кейбір
облыстардың стратегиялық маңызы бар жерлерінде орналастырылады. Егер біз
станцияларды бір желіге біріктірудің бүкіл құнын төмендеткіміз келсе, онда
станциялар төбесі болатын, ал оларды қосатын қабырғалары біріктіру құнын
көрсететін граф құруға болады. Бұл графтың минимальдық діңгекті шежіресі,
қандай станцияларды біріктіру құны мүмкіндігіне төмен болған жағдайда
қосуға болатынын көрсетеді. Графтағы ең қысқа жол табу мақсатында осындай
қолданылу табады: мысалы, осы есептің шешімін табу автомобиль сапарын
жоспарлауға көмектеседі немесе компьютер желілері бойынша хабарлама
жіберуге болады.
Үлкен компьютер желілерінің маңызды сипаттамасы болып олардың
қолданудағы сенімділігі. Біз желінің бір түйіні істен шықса да жұмыс істеу
қабілетін жоғалтпағанын қалар едік. Жорта айтқанда, желідегі станциялар
әртүрлі жолдармен қосылу керек, себебі кез келген бір жол бұзылса да
ақпарат беру мүмкіндігі сақталу керек. Ол графтың жолдағы бір бөлімінен
екінші бөліміне кез келген жолдағы төюелерді іздейді. Компьютер желісінде
осындай түйіндердің бұзылуы желідегі байланыстылықтың бұзылуына әкеліп
соғады.

1.3. Графты көрсетудегі мәліметтер құрылымы

Графтар және орграфтар туралы ақпаратты екі әдіспен сақтауға болады:
түйіскен матрицалар түрінде әлде түйісулер тізімі түрінде Бұл параграфта
графтар және орграфтар бірдей көрсетілгендіктен, біз олар үшін біз ортақ
граф терминін қолданамыз. Тағы да біз қолданылатын ақпарат сақтау әдістер
графтар мен орграфтарды өңдеу айырмашылықтарын жоятынын көреміз.
Түйісу матрицалары графтың қабырғалары туралы ақпараттарға тез жетуді
қамтамасыз етеді. Бірақ, егер графтарда қабырға аз болса, онда матрицаларда
толтырылған ұяларға қарағанда бос ұялар көбірек болады. Түйісу тізімінің
ұзындығы графтағы қабырғалар санына пропорционалды болады, бірақ тізімді
пайдаланған кезде қабырға туралы ақпарат алу уақыты ұзарады.
Бұл әдістердің біреуі де бір-біріне алдын ала артық емес. Керекті
әдісті таңдау негізінде, алгоритммен өңделетін граф туралы ақпарат жатады.
Егер графта төбелер көп болса, сонымен қатар, олардың әрқайсысы аз ғана
төбелер санымен байланыста болса, түйісу тізімі тиімді болады. Себебі ол
өте аз орын алады, ал қаралатын қабырғалар тізімі ықшамды. Егер графта
төбелер саны аз болса, онда түйісу матрицасын пайдаланған жақсы: ал үлкен
болмайды және сиретілген графты матрица түрінде сақтағанда жоғалу мардымсыз
болады. Егер графта қабырға көп, ал толықтау болса, онда түйісу матрицасы
графта сақтаудың ең жақсы әдісі болады.
Матрица мен түйісу тізімін пайдалану келесі бөлімдерде жан-жақты
жазылған.

Түйісу матрицалары.

G= (V,E) Графының [V]=N төбе саны бар AdyMat түйісу матрицасы NxN
көлемді екі өлшемді массив түрінде жазылады. Осы массивтің әр [i,j]
ұяшығында 0 мәні жазылады, бұл тек егер Ui төбесінен Uj төбесіне қабырға
жүргенде сонда ұяшықта 1 мәні жазылған жағдайлардан басқа сәттерде ғана.
Дәлірек айтқанда:

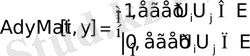
барлық i мен j 1 ден N ге дейін

Көтеріңкі графтың әлде орграфтың түйісу матрицасының ұяшығы құрамында
шексіз болады, егер сәйкес қабырға жоқ болса, ал қалған басқа жағдайларда
оның мәні қабырға салмағын тең. Осындай матрицаның диогональдық элементері
0-ге тең, себебі төбеден өзіне қайтатын сапары ештеңе тұрмайды.

Түйісу тізімі

[V]=N саны бар G=(V,E) графының Adibist түйісу тізімі ұзындығы N бір
өлшемді массив түрінде жазылады. Соның әр элементы тізімге сілтеме түрінде
болады. Осындай тізім графтың әр төбесіне бекітілген және ол графтың осы
төбесімен көрші әр төбесіне бір-бірден элемент ұстайды.
6.3 суретінде 6.1 суретіндегі граф пен орграфтың түйісу тізімін
бейнелейді. Көтеріңкі графтың түйісу тізімінің элементі құрамында қабырға
салмағын сақтайтын қосымша алаң бар.

Тереңдікке және деңгейлерді аралау алгоритмі

Графтармен жұмыс істегенде әр төбеде бір реттен кейбір әрекеттерді
жиі орындауға тура келеді. Мысалы, ақпараттың кейбір бөлігін желідегі әр
компьютерге жіберу керек және сонымен қатар кейбір компьютерге екі рет
кіргіземіз келмейді. Осындай жағдайларда егер біз ақпаратты тарату үшін
емес, жинағымыз келгенде де пайда болады.
Осындай аралауды екі әртүрлі тәсілмен істеуге болады. Тереңдікті
аралау кезінде таңдалған жолмен өту барша мүмкін тереңдікке дейін іске
асырылады, ал деңгейлер бойынша аралауда біз барша мүмкіндік бар бағыттарда
бірқалыпты қозғаламыз. Енді осы екі тәсілді жанжақты қарайық. Екі жағдайда
да біз басталу нүктесі ретінде графтың бір төбесін таңдаймыз. Төменде
түйінге кіру деп әрбір төбеде істеуге қажет әрекеттерді орындау деп
түсінмезі. Мысалы, егер іздеу жүріп жатқанда, біз осы түйінге кірдік деген
сөз, біз онда керекті ақпарат барлығын тексердік деген сөз. Аталған әдістер
еш өзгеріссіз бағдарланған, сондай-ақ бағдарланбаған графтарда жұмыс істей
береді. Біз оларды бағдарланбаған графтар арқылы көрсетеміз.
Осы әдістердің кез келгенінің көмегімен қаралып отырған граф
байланылғандығын тексеруге болады. Графты аралаған кезінде өткен
түйіндердің тізімін жасауға болады, ал аралау аяқталғаннан кейін жасалған
тізімді графтың барлық түйіндердің тізімімен салыстыруға болады. Егер тізім
тек қана сол элеметтен тұратын болса, онда граф байланысты. Егер графта
бастанғы төбеден жете алмайтын төбелер болса, онда граф байланысыз.

Тереңдікке аралау

Тереңдікке аралау барысында біз бірінші түйінге жетеміз, одан кейін
тұйыққа тірелгенше графтың қабырғалары бойымен жүреміз. Бағдарланбаған
графтың түйіні, егер біз осы түйінге түйіскен басқа түйіндерге кіріп
болғаннан кейін, тұйық болып табылады. Бағдарланған графта өзінен шығатын
қабырғалары жоқ түйінде тұйық болады.
Тұйыққа тірелгеннен кейін, біз әлі бармаған төбеге көрші төбеге
жеткенше кері қайтамыз да, осыдан кейін жаңа бағытта жылжимыз. Біз бастанғы
нүктеге түйіскен бүкіл төбелерде болып оған қайтқанда процесс аяқталған
болып саналады.
Осы және басқа алгоритмдарды көрсеткенде, екі төбеден біреуінен
таңдауда, біз әрқашан кішілеу белгісі бар төбені таңдаймыз. Алгоритмді іске
асыру кезінде таңдау графтың қабырғаларын сақтау тәсілі таңдау түрін
белгілейді. 6.4 суретіндегі графты қарайық. Бір төбеден тереңдікке аралауды
бастап, біз одан кейін 2, 3, 4, 5, 6 төбелерінде болып, тұыққа тірелеміз.
Одан кейін 7 төбесіне қайтуға тура келеді, онда біз 8 төбені шолмағымыз
анықталады. Бірақ осы төбеден өтіп, біз бірден тағы да тұыққа тірелеміз. 4
төбеге қайтқанда біз 9 төбенің шолынбау қалғанын көреміз, енді оған бару
бізді тағы да тұйыққа әкеледі. Бүкіл көрші төбелер түгел шолығандықтан біз
қайтадан бастапқы нүктеге қайтамыз; аралау осымен аяқталады

1.4. Графикалық торлар

Графикалық торлар-бұл техника мен ұйымдастыру жүйелерді графика арқылы
көрсету әдісі. Ғылыми жұмыстарды графикамен көркемдеу нақты мәнін
көрнекілігімен көрсетеді, кей жағдайда қойылған міндеттің шешімін табуды
тіпті жеңілдетеді. Әр түрлі көрнекілікті графикамен көрсетудің әмбебап
құралы ретінде граф табылады. Мұнда граф деп, торап пен қырлардың жиынтығын
түсінеді. (1-сурет). Түрлі торап пен қабырғалардың сан алуан құрамалары
,мүмкін болатын графтар мен олардың қолдану жолдарын көрсетеді. Қабырға
бағыттары көрсетілмеген, ал тораптар төртбұрыш түріне келтірілген графтар
техникалық жүйелердің құрылымын көрсетуге қолданылатын блоксхемаларды
суреттейді. 1-суретте көрсетілген графты ағаш деп атайды. Мұндай ағаш-граф
арқылы толық санды бағдарламалау міндетін қарастыратын бұтақтар мен
шекаралар әдісін қөркемдейді. Егер ағаштағы баоылық тораптар бірнеше
деңгейге бөлінсе, онда оны көп деңгейлі иерархия жүйесі деп білеміз. Егер
граф қабырғасы бағытқа ие болса, яғни доға арқылы жүзеге асса, ондай графты
тор деп атайды. Тор арқылы орын ауыстыру немесе уақыт бойында орындалатын
жұмыстардың тиімді шешімін табудың түрлі міндеттері көрсетіледі. Тор
доғалардың құрылым мен параметрлері сипатталады. Тор құрылымы, немесе оны
топология деп атайды, байланысшы доғалардың юағытын және тораптарын өзара
қалай байланысатынын көрсетеді. Әрбір торапты реттік санмен белгілейді.
Бастапқы торапты бастау деп,ал соңғысын ағаш деп атайды.

1- сурет

Доғаны қосарланған индекспен белгілеиді. Жалпы i-j деп көрсетеді, онда i
доға шығатын тораптың нөмеірі, j-доға кіретін торап нөмірі деп
қабылданады. Әрбір доға өз сипатына ие болады. Мысалы, ti – j доға бойымен
қозғалу мерізімі, ci-j- орын ауыстыру құны, di-j доғаның өткізу қабілеті,
т.б.

2 - сурет

Тордың құрылымын және доға сипатын біле отырып, ғылыми-ерттеулерде жиі
кездесетін түрлі есептерді шешуге болады.

1. Жылжу есептері.
а) Коммивояжер есебі 3 - суретте көрсетілгендей, орналасқан 5 пункт бар,
олардың бір-бірімен байланыс арқылы әр бір пункттен кез келген басқа
пунктке өтуге болады. Мұнда қойылатын талап: белгілі бір пункттен шығып
ең аз уақыт ішінде барлық пункттерді айналып шығу.

3 - сурет

Бұл есепті шешу үшін математикалық модель құраймыз. Ол үшін белгілерді
енгіземіз:i және j-кіру-шығу пункттерір нөмірі, tij- I пунктіне жүру
уақыты
4 - кестеден көрінетіндей, tij жалпы кері бағыттағы tij уақытына тең
болмайды.

4 -кесте
I пунктінен J пунктіне
1 2 3 4 5
1 0 10 25 25 10
2 1 0 10 15 2
3 8 9 0 20 10
4 14 10 24 0 15
5 10 8 25 27 0

Математикалық модельді құру үшін бізге белгілі қисынды буль ауыспалы
мәндерді аламыз.

деп қабылдаймыз.

4.9-сурет

5 - сурет

Модель құраймыз. Пункт 1-ден кез-келген төрт пункттің бірекіне шығуға
немесе осы пункттің өзінде қалуға болады. (4.9-сурет). Бұл жағдайда бір
бағытта шығуға болады. Бұл шартты мынадай түрде жазамыз:

δ 11+δ 12+δ 13+δ14+δ15=1

жалпы бұл шарт былай жазылады:

5
∑δ
j-1

Егер пункт 1-ден кез келген i-пунктіне шығатын болсақ, онда ол былай
көрсетіледі:

5
∑ δij=1,i=1,5 (6)

j=1

Бұл тәуелділіктер бастапқы талапты орындауға мүмкіндік береді: әрбір
пункттен тек бір қана және бір бағытта жүруге болады. Бағдартың ең аз
ұзақтық талабын мақсатты функция түрінде жазамыз:

А=t11δ11+t112δ12+t13δ13+t14δ14+t15δ 15t+t21δ21+t22δ22+...+t55δ55→ min, (7)

Мұнда tij мәндері 4 - кестеден алынады, ал δij ізделіеген ауыспалы мәндер
болып келеді. Жазудың қысқартылған түріне көшсек, ол огсындай болады:

(8)

Жүйе шешу нәтежесінде (8) келесі мәндерді аламыз: δ15=δ52+δ23+δ34+δ41=1
қалғаны F=10+8+10+20+14=62 болады. Бұл бағдар 4.10-суретте көрсетілген.

9-сурет

10 - сурет

Егер жеке жағдайдан айырылсақ, есептің n пункттердің айналып шығу жалпы
талабын орындау үшін былай жазамыз:

(11)

Сонымен қоса 10 және 11 шарттарды қанағаттандыратын бағдар бар: жылжу
барысында үзілістер болады, бірақ әр пункттен бір рет кіріп-шығу шарты
орындалады (9 - сурет). (10) және (11( жүйесі қажетті, бірақ жеткіліксіз
шарттарды қамтиды. Ол үшін қосымша N шектеулер енгізіледі: N=(n-1)²-(n-
1), әр бір шектеу мынадай түрде болады:

Yi-yjnδij≤n-1; i=2,n; j=2,n-∞yij∞.

(12)

Біздің мысалда мұндай қосымша шектеулер саны N=(5-1)²-(5-1)=12 тең
болады. Олардың түрі мынадай болып келеді.

Y2 − y3 + 5δ23 ≤ 4 ; y2 − y4 + 5δ2 4≤ 4 ; y2 – y5 + 5δ25 ≤ 4 ;
Y3 – y2 + 5δ32 ≤ 4 ; ...; y5 – y4+5δ54≤4.

Сонымен есептің математикалық моделі ретінде (11) жүйесі мен қосымша
шектеулер (12) саналады. Осындай коммивояжер есебі тәріздес ғылыми
мәселерді шешуде туындайтын көптеген есептер бар-қайсыбір бұйымды
өндеудің технологиялық үрдісін тиімді ұйымдастыру, базаларды
қамтамасыздандыру,ұйымдастыру және т.б.
б) Ең қысқа жолды іздеу есебі. 10-суретте көрсетілгендей А пунктінен В
пунктіне көп жолдар барады.

13 - сурет

Кейбір жолдарда қозғалыс бір жақты, кейбіреуінде екі жақты. Екі пунктің
арасындағы жол ұзындығы әрбір доғада көрсетілген. сонда А пунктінен В
пунктіне ең қысқа жол табу қажет. Математикалық модель құраймыз. 14
-суретте көрсетілгендей пунктіне кіретін-шығатын доғаларды болжаймдайық:

14 - сурет

Бағдар үзіліссіз болу үшін әрбір пунктке тек бір доға кіріп-шығу керек.
Бұл талап егер төмендегідей шарттар болса орындалады: Пунктке кіретін
доғалар үшін:

p
Nibx=∑δkj=1 (15)
k=1

Мұнда δki k пунктінен шығатын және i пунктіне кіретін доғағак сәйкес
келеді.

(12) шарт i пункітінен шығатын және j тіне кіретін доғаға сәйкес келеді:

(4.20) шарты i пунктіне тек бір доғамен шығуды қамтиды.
Бағдардың барлық пунктерін бастапқы, өткелі және соңғы деп бөлуге болады.

Бұл пункттер үшін келесі шарт орындалу керек.

(16)

Шынымен, бастапқы пуект Nвх =0. Демек, бастапқы пункттен тек бір доға
шығу керек. Өткелі пункттер үшін Niвх=Niвых шарт бір доғамен шеғу-кіруді
қамтиды. Соңғы пункт үшін Nвых= 0 кіруді бір

доғамен қамтиды. Сонымен (15 - 16) шарттары үзіліссіз бағдар талабын
орындайды. Мұнымен қатар бағдар ең аз ұзындыққа ие болу үшін мақсатты
функцияны қосамыз:

F=∑ ∑ Cijδij (17)
i j

Мұнда Cij –жол ұзындығы, ол барлық доғаларды қамтиды "Шектеулер" мен
мақсатты функцияны қосқанда жүйені былай жазамыз:

F= ∑ ∑Cijδij→min

i j

Пункт δ12 δ13 δ14 δ23 δ25 δ32 Δ34 δ35 δ43 δ45 белгі Оң жол
F 2 6 8 3 7 5 1 5 4 2 min 1 -1 -1 -1 = -
1 2 1 -1 -1 1 = 0 3 1 1 -1 -1 -1 1 =
0 4 1 -1 -1 = 0 5 1 1 1 = 1

δij ≥ 0

бұл ауыспалы мәндерге теріс емес талабының қойылғаны жеткілікті, яғыни

δij ≥ 0

δij= 0 немесе δij= 1 талабын қоймаса да болады, себебі мұндай
есептерде шектеулер арқасында шешу барысында δij тек 0 немесе 1 мәнін
алуды қамтиды.

11 берілген суреттегі есепке 17 жүйесін құраймыз, ыңғайлы болу үшін бұл
жүйені 5 - кесте ретінде көрсетеміз.

Мұндай әрбір доғаға ауыспалы мән, әрбір пунктке шектеу сәйкес келеді.
Кестеде көрсетілген шамалар ауыспалы мәндердің шектеулерге кіретін
коэффициентерін нұсқайды. Мысалға, 2 пунктін шектер түрі δ12 – δ23 – δ25
+δ32 = 0 болады, мұнда (+) белгісі кіретін доғалар алынада, (-) белгісі
шығатын доғалар алынада қойылған. Есепті шешу нәтежесінде келесі мәндерді
аламыз: δ12=δ23=δ34=δ45= 1. Қалған δij= 0 ең қысқа бағдар δij= 1
доғаларды қамтиды. Бұл бағдар 4.14-суретте көрсетілген. барлық
пункттерден өтуіне қарамастан, оның ұзындығы ең аз
мәнге
F=2+3+1+2=8. Байқауға болатындай, бір өтпелі пункттен өтетін бағдартар ең
ұзын болып келеді. (1-2-5=2+7+9=1-3-5=6+4=10, 1-4-5=8+2=10).

18 - сурет

Практикалық есептерде үлкен бағдарларды байқау қиын, ал мүмкін варианттарды
жалпы терудің күрделілігі бар. Сондықтан қысқа жолды жолды табудың бұл
тәсілі ең тиімді және қарапайым болып табылады. Жалпы жағдайларда түрлі
практикалық есептерді шешуде i-j доғаларға түрлі мағыналарды беруге болады:
ұзақтық, құны, еңбек көлемі т.б. Осындай қысқа бағдар таңдау есептері
тәріздес деп, ғылыми техникалық мәселелерді шешуде туындайтын түрлі
есептерді қабылдауға болады.

2.1. Сыртқы программалар мен оларды MS Excel ортасында пайдайдалану

MS Excel программасының функционалдығын кеңейтетін VBA тілінде
програмалар мен функцияларды осы программаларды текстермен модульді
қамтитын кітаптарда пайдалану үшін кіру мүмкіндігін ашық деп көрсетуге
болады. MSExcel программасы басқа мүмкіндікке де ие болады-басқа
программалау тілінде жазылған және жеке динамикалық құрастыру кітапханасы
(DLL) түрінде жазылған функцияларды пайдалану. Осы бөлімде әртүрлі
программалау тілінде жазылған ішкі программалар мен функцияларды MS Excel
ортасында пайдалану варианттары қарастырылады.

2.1.1 Borland Delphi ортасында сыртқы функциялар құру және оны MS Excel
ортасында қолдану

MS Excel ортасында VBA сыртқы программаларды пайдалану тәсілдері
программа тексттеріне сәйкес қосымша модульдерді MS Excel жұмыс кітабындағы
кемшіліктерді туындатады. Бұл қолайсыздықтан басқа программалау тілдерінде
жазылған және жеке динамикалық компоновка кітапханасы (DLL) түрінде
жинақталған функцияларды пайдалану негізінде құтылуға болады. DLL
кітапханасы құру үшін VBA тілі мұндай кітапхананы құруға мүмкіндік
бермейтіндіктен, интеграцияланған программалау ортасын қосымша пайдалануға
мүмкіндік бермейді. Мұндай орта ретінде Borland Delphi немес MS Visual
Studio. NET6 ортасын пайдалануға болады. Бұл бөлімде Borland Delphi7
ортасында пайдаланушы функциясын құру процесі қарастыылады.

Ескерту

Қарастырылатын материал интеграцияланған ортада программалау тәжірибесі
бар пайдаланушыларға арналған. Сәйкес ортанаың басты менюінің операциялары
мен жұмысшы интерфейс терезенің қызметі жайлы толық ақпарат
пайдаланушыларды қызықтырады. Кітапта келтірілген материалдар есепті шешу
үшін жеткілікті.
Екі өлшемді экспоненциалды мақсаттық функция үшін (2.1) формулаға
сәйкес 0,1-ден бастап берілген параметрдің өзгер интервалымен 1-мен
аяқталатын а параметрінің өсетін мәні үшін тізбекті қосуды орындау қажет.
Осы есеп Borland Delphi7 ортасында Object Pascal тіліндегі арнайы программа
көмегімен шешіледі.
Borland Delphi7 ортасында сәйкесі программаны құру үшін алдымен оны
пайдаланушының компьютеріне орнату керек. Сосын Delphi редакторының басты
менюінднгі: File (Файл)New (Жаңа) Other (Басқа) операцияларды орындаймыз,
нәтежесінде Delphi ортасында (2.11-сурет) жаңа жоба құру шеберінің диалогты
терезесі ашыла

2.11-сурет Delphi ортасында жоба құру шеберінің терезесінде DLL Wizard(DDL
шебері) текс программасын таңдау керек. OK батырмасын басамыз. Бұл
операцияны орындау нәтежесін де My DLL Delphi деген атпен берілген жаңа
жоба құрылады.Delphi редакторыныда қажетті қызметші опреаторларыды қамтитын
DLL құру жобасының коды бар терезе пайда болды

Function MinPath (N: Integer; C: array of Real) : PChar; export; stdcall;
Var
dis : array of array of Real; dis – матрица расстояний графа
Vmin : array of Integer;
Vpom, Vect : array of Integer;
S1, S: String;
I, j, k, im, jm : Integer;
Rec : Real;
Begin
Setlength (Vmin, N) ;
Setlength (Vpom, N) ;
Setlength (Vect , N) ;
Setlength (dis , N) ;
for i:=0 to N-1 do
Setlength (dis [i] , N) ;
for i :=0 to N-1 do
for j :=0 to N-1 do
dis [i ,j] :=C[i*n+j+1] ;
for i :=0 to N-1 do
begin
Vmin [i] :=1000; иектор минимальных расстояний
Vpom [i] :=0 1- постоянные пометки,0 – временные пометки
Vect [i] :=0 минимальный путь
end;
Vmin [0] :=0 ;
Vpom [0] :=1;
Vect [0] :=0;
k := 0;
im := 0;
s1:= ‘’ ;
repeat
for i :=0 to N-1 do
for j :=i+1 to N-1 do
if (dis [i,j] 0) and (Vpom [j] =0) fnd (Vmin[j]+Vmin [i] +
Vmin [i]) then
begin
Vmin [j] := dis [i,j] + Vmin [i];
Vect [j] := i ;
end;
rec := 1000;
for i := 1 to N-1 do
if (Vpom[i] =0) fnd (rec Vmin [i]) then
im:= i;
Vpom [i] :=1;
k :=k+1;
until (k=n-1) ;
s :=’ Минимальный путъ из 1-й вершину ‘+intTostr (n)+’ : ‘ ;
rec :=0 ;
for i :=0 to N-1 do
Vhom [im] :=0;
Jm := N-1 ;
For j := N-1 downto 1 do
If (j = jm) then
begin
jm := Vect [j];
Vpom [jm] := j;
end;
for i :=0 to N-2 do
if (Vpom [i] 0) then
begin
s1 := s1+’(‘+FloatTostr (i+1)+’,’+ FloatTostr
(Vpom[i]+1)+’),’;
rec := rec+dis [i, Vpom[i]];
end;
Result :=Pchar (s+s1+’ Fmin =’ + FloatTostr (rec));
Vmin :=NIL;
Vpom :=NIL;
Vect :=NIL;
dis :=NIL;
end;
exports MinPath;

2.2. Delphi ортасында DLL құруға арналған жаңа проектінің терезесі

Екіөлшемді экспоненциалды функцияны есептеу үшін Delphi кодты редактордың
begin-end аяқтаушы блогының алдына Паскаль тілінде келесі мәтіндік
бағдарламаны енгіземіз (суреттің 2.2)
2.2. Паскаль тілінде екі өлшемді экспоненциалды функцияны есептеу
бағдарламасы.

function ExpFunc2 (x1, x2: Real) : Real; export; stdcall
var
sum, Func : Real;
i : Byte;
begin
Sum := 0.0;
for i := 1 To 10 do
begin
Func:= ((Exp(-0.1*i*x1)- Exp(- 0. 1* i* x2))- (Exp(-i)));
Sum := Sum + Func* Func;
Result := sum;
end;
exports ExpFunc2;

Бұл бағдарлама x1 және x2 екі формалды параметрі бар: ExpFunec2 функциясын
береді. Бұл функцияның бағдарламасының мәтіні Паскаль тіліндегі функцияны
хабарлау үшін қолданылатын Function-стандартты операторының көлемімен
басталады, онда кейін жақшаның ішіндеформальды параметірлері жазылған
ExpFunce2 функциясының аты көрсетіледі. Функцияның атынан кейін екі кілттін
сөз жазылады: export-берілген функцияның басқа қосымшаларда да қолданылуы
мүмкін екендігін көрсетеді; ctdcfll-аты шақырудың стандартты тәсілін
көрсету үшін жазылады. Функция мәтіні айнымалдардың типін хабарлаудан
басталады, бұл кезде функция Real айнымалысы типіне сәйкес келетін негізгі
мәнән қайтарады. Негізінде екі өлшемді экспоненциялды функция мәнінің
есептелінуі x1 және x2 тәуелсіз айнымаларының екі мәні үшін For-To-Do
циклінің көлемімен іске асырылады, ол “i” айнымалысы арқылы тізбектеле
орындалады. Қарапайым экспоненциалды функцияны есептеу үшін Бір аргументті
Exp функциясы қолданылады. Re,sult:=s операторы берілген функцияның
қайтымды мәтінін береді. Ақырында, соңғы Export Exp Func2 операторы
функцияға басқа қосымшалардан байланысқа шығуға арналған функцияның атын
көрсету үшін қызмет етеді.My DLL Delphi.dpr файылдын аты бар мәтіндік
бағдарламаның Delphi редакторындағы сыртқы түрі 2.13-суретте бейнеленген.
Delphi редакторында функцияның мәтіндік бағдарламасын жазғаннан кейін
проектіні компилициялау және жинақтауды орындау қажет. Бағдарлама
мәтініндегі қажетті шығару мақсатында проектіні алдын ала мақсатты түрде
компиляцяны орындау керек, ол үшін Delphi редакторының бас мәрізінде
келесі операцияны орындаймыз: Project (Проект)Conpile MyDLL
Delphi(Компилировать MyDLL Delphi). Бұл жағдайда қате бар болса олар
көрсетіледі, ал олар туралы ақиғат Delphiедакторының арнайы терезесінде
көрініс береді. Жіберілген конпектілерді жойғаннан кейін проектіні жинақтау
орындалады, ол үшін Delphi редакторының бас мәзірінде келесі операцияны
орындау керек: Projekt (Проект) Build My DLL Delphi (Создать MyDLL
Delphi). Мұның нәтежесінде берілген проектінің файылдар аты бар бумасында
MyDLL Delphi.del атты файл құрылады, ол екі өлшемді экспоненциялды
функцияның мәнін есептеуге мүмкіндік беретін орындалушы коды бар файл.
Берілген функцияны MS Excel ортасында пайдалану үшін MyDLL Delphi. del
файлы MS Windos операциясына жүйесінің жүйелік бумасында көшіріп алу
қажет. Мұндай бума ретінде сол дискідегі Windos атты бумадағы System атты
буманы алуға болады, ол OC-та орнатылған Осы әрекеттер орнатылғаннан кейін
Exp Func2 фукциясы MS Excel бағдарламасының жұмысшы парағындағы ұяшықтарда
пайдалануға болатын формулалар түріне ауысады. Бұл жағдайда MS Excel
бағдарламасын қосымша баптаудың ешқандай қажеті жоқ. Exp Func2 функциясы
берілген кітаптың кез-келген жұмысшы парағының ұяшығынан тікелей
шақырылады. Бұл жағдайда MS Excel бағдарламасының ұяшықтарындағы берілген
формуланың арнайы шақыру форматын пайдаланған дұрыс. Бұл мақсатта қажетті
ұяшықты бөліп алып, функция шеберін шақыру қажет, ол үшін вызвать (шақыру )
функциясын таңдап аламыз. Бұл функция сыртқы кітапханадан функция шақыруға
арналған.

Ескерту: MS Exel бағдарламасының әртүрлі версияларында вызвать (шақыру)
функциясы арнайы зерттеулер көзі пайдаланылады, ол бағдарламадағы. Мысалға
MS Excel-деу версиясында бұл функция жақсы жұмыс істейді,MS Excel-2000
верциясында бұл функцияны шақыруда қиындық туындайды. Ал MSExcel-2003
верциясында бұл функция қолданылатын функциялар тізімінде мүлде жоқ. Бұдан
жыл өткен ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.