Нюрнберг қайшысы типті төменгі жетекті жүк көтергіш механизмдер жетегін оптималдау

Жоспар

МАЗМҰНЫ

Кіріспе 6
1 «Нюрнберг қайшысы» типті жүк көтергіш механизмдердің тиімділігін талдау 8
1.1 Патенттік анализ 8
2 “Нюрнберг қайшысы” типті төменгі жетекті жүк көтергіш механизмдер жетегін оптималдау 22

3. Тербелмелі гидроцилиндрлі жүк көтеруші механизмдердің күштік анализі
3.1. Күштік анализдің негізгі өрнектері
3.2.Айнымалыларды варияциялаудың ЛПτ.тізбектер әдісі
3.3 Сандық мәндер

4 Сыбайлас емес ҚССҚБ сұлбалы жүк көтеруші механизм жетегін оптималдау
4.1 CG буынымен сырғақты гидроцилиндр арқылы байланыстыру варианты
4.2 KQL гидроцилиндрі CB жәнеFE сырықтарын қосады.
4.3 KQL гидроцилиндр FE сырығын В сырғақпен қосады
4.4 KQL гидроцилиндр FE сырығын тіреумен қосады
4.5 KQL гидроцилиндрі CG және ОЕ сырықтарын қосады

ҚОРЫТЫНДЫ
ӘДЕБИЕТТЕР ТІЗІМІ

Пән: Транспорт
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 71 бет
Таңдаулыға:

КІРІСПЕ

Жұмыстың өзектілігі. Машинажасау саласын дамыту қазіргі заман
талаптарына сай келетін жаңа инновациялық технологияларды енгізудің басты
салаларының бірі болып табылады. Жаңа машиналар мен қондырғыларды жасау
үшін олардың жобалау әдістерін жетілдіру керек. Машина мен механизмдерді
тиімді жобалудың академик У.А.Жолдасбеков бастауында тұрған мектебі бар,
бұл еңбектерде [1-3] жазық иінтіректі механизмдерді кинематикалық және
динамикалық критерийлер бойынша синтездеудің және анализдің жалпы әдістері
жасалған. Осы әдістерді өндіріске қажетті нақты механизмдер жобалауға
пайдалану қажет.
Көптеген технологиялық процесстерде, әсіресе құрылыс-монтаж
жұмыстарында, жөндеу-қалпына келтіру жұмыстарында механикаландырылған жүк
көтергіштерге мұқтаждық үлкен. Бірақ өкінішке орай қазіргі өндірістік және
құрылыс объектерінде мосы (козел) типті, немесе құрылыс шарбақтары
(строительные леса) типті ағаш немесе метал конструкциялар жиі
қолданылады. Бұл конструкциялар берік емес, оларды құрыпмонтаждауға көп
уақыт өтеді, ал матеиалды қажетті биіктікке көтеру қолмен жүргізіледі.
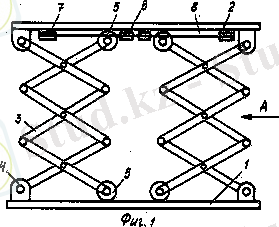
Маркетингтік анализ көрсеткендей, біздің отандық нарықта жүк көтергіш
механизмдерді шығаратын өз өндірушілеріміз жоқ, ал қолданылатын Нюрнберг
қайшылары типті (Nurnberg scissor) көтергіштер шетелде шығарылады.
Алайда бұл типті көтергіш платформалар конструкцияларының қатаңдығы
төмен болғандықтан өте қауіпті, аударылып кету қауіпі жоғары. Сондай-ақ бұл
жүк көтергіш қондырғылар өте ауыр. Оның негізгі себебі төменгі транспорттық
жиналған күйінде механизм сингуляр күйге аса жақын орналасқан, сондықтан
кинематикалық жұптардағы реакцияларда өте үлкен, ал теңгеруші күштің мәні
өте жоғары. Мысалы кейбір конструкцияларда теңгеруші күш пайдалы салмақпен
салыстырғанда 16 есе жоғары екенін көруге болады.
Сондықтан осындай жүк көтергіш механизмдердегі гидроцилиндрлік
тізбекті тиімді етіп жобалау әдістерін жасау керек. Жүк көтергіштігі
жоғары, теңгеруші күш аз және салмағы жеңіл механизм түрлерін жасау өзекті
мәселе болып табылады.
Дипломдық жұмыстың мақсаты: жазық иінтіректі механизмнің жетектегіш
тізбегін синтездеудің күш берілісі тиімді болатын әдісін жасау және тиімді
жобалау. Бұл мақсатқа жету үшін мынадай есептерді шығару қажет [4, 5].
1. Жүк көтергіш механизмдер бойынша патенттік анализ жүргізу, InterNet
көздері бойынша салыстрмалы шолу жасау (Nurnberg-scissor type Platform,
Hoisting Device, Lifting Device, механикаландырылған құрлыс көтергіштері
(строительные леса), т.б.)
2."Нюрнберг қайшысы" тиіпті жазық иінтіректі механизімді
кинестатикалық талдау.
3. Жазық иінтіректі механизмнің теңгеруші күшін табу.
▪ төменгі жетектегіш үшін;
▪ теңселмелі жетектегіш (гидроцилиндр) үшін;
▪ сыбайлас емес буындарды қосатын жетектегіш үшін;
4. Жетектегіш кинематикалық тізбегін синтездеу және синтез нәтижелерін
талдау.

1 Нюрнберг қайшысы типті жүк көтергіш механизмдердің тиімділігін талдау

1.1 Патенттік анализ

Қарастырылған 4 жылдағы патентік анализде машинажасау саласынадағы жүк
көтергіш-транспортқа жататын қондырғылары, соның ішінде негізінен көп
қолданылатын Нюрнберг қайшысы типті жүк көтергіш қаралды. Қазақстандағы
бірнеше фирмалар ОАО Пожтехника фирмаларының Haulotte жүк көтергіш
қондырғыларын сатумен, жалға берумен, сервисті қызмет етуімен шұғылданады.
Көптеген Ресей фирмаларында жүк көтергіш қондырғылары жасалады. Ресей
федерациясының территориясындағы UpRight Inc, Terex Corp., TADANO Ltd., JLG
Industries, Iteco Spa, AIRTEK, AIRO Tigieffe Srl, Aichi Corp., MEC Corp.,
Genie, Dinolift Corp., Nostolift Corp., Translyft және басқа фирмалары жүк
көтергіш қондырғыларын сату және жалға беруді жүзеге асырған. Тап осы
фирмалардың ұсынып отырған жүк көтергіштердің биіктігі 6 метрден жоғары,
ғимараттың ішіндегі емес, сыртқы ангарлық немесе қоймалық сияқты жұмыстарды
атқаруға арналған, аккумулятор немесе дизель қозғалтқышпен жұмыс істейтін
қондырғыларды ұсынады.
Қазіргі бар аналогтарды салыстырамыз. 1-суреттегі Нюрнберг қайшысы
типті жүк көтергіштің (Nurnberg scissor-type LM-1000) негізгі
сипаттамалары 1-кестеде берілген. 2-суретте ТТ3000ФА жүк көтергіш
столы берілген, ал сипаттамалары 2-кестеде және Maniaccess XE-XEL
сериялы жүк көтеруші механизмі 3-суретте көрсетілген. Бұл жүк
көтергіштердің кемшілігі: жоғарға жайында платформаның орнықсыздығы,
жиналған жайнда жетектегі күш берілісі рациональды емес, материал
сиымдылығы жоғары, жүк көтергіштігі аз, жүк көтергіш қондырғының салмағы
мен көтеретін жүктің салмағының арақатынасы 0,43 конструкциялары қиын,
бағасы да қымбат.

Кесте 1.1 Нюрнберг қайшысы типті LM-1000 жүк көтергіштің спаттамалары
КөтергіштіСтол габариттері, мм Сал Гидроцилиндрлер
ң аты мағ
ы,
(кг
)
Биіктігі БиіктБиіктКөтеру гц түрі саны
ік, ік, биікгі
min max
TLD1000Б 1300x1000366 1966 1600 430HC 80-340 1
TMD1000A 1700x130000 550 150 800HC100-320 1

Сурет 1.1 Нюрнберг қайшысы-типті жүк көтергіш
(Nurnberg scissor-type LM-1000)

1.2 кесте - ТТ3000ФА жүк көтергіш сипаттамалары
Жүк көтергіштігі, кг. 3000 дейін
Платформаның өлшемі, мм 2500х2000
Көтерілетін биіктігі, мм 1956 дейін
Высота в сложенном состоянии, мм 356
Толық биіктікке көтерілу уақыты, сек. 40
Эл. қозғалтқыштын қуаты, кВт 2,2
Салмағы, кг 1148

1.2 сурет - ТТ3000ФА жүк көтергіш стол

1.3 сурет - Maniaccess XE-XEL -сериялы жүк көтеруші механизмі

1.4-суретте жүк көтергіш берілген [6]. Ол негізден, жүк салатын
платформадан, арасында және бір-біріне қарама-қарсы негізгі және қосымша
жұпты топсалы иінтіректі механизм орналасқан. Әр қайсысы иінтіректі қиып
өтетін екі топсалы жұптары бар, бір соңы гидроцилиндр бағыттауышқа
құрастырылған, платформа мен негізге бекітілген жәнындағы иінтіректің басқа
соңдары топсалы байланысқан, иінтіректің орынауыстыратын соңдары топсалы
роликтің шетмойынды құралған негіздегі бағыттауышқа орнатылған және жүк
көтергіш платформадан. Электромеханикалық келтіру иінтіректі қозғалтуға
негізделген, құралған айырмашылығы жүк көтергіш платформа қаңқа түрінде
бойлық және көлденең арқалық құралған.
Платформаның, қаңқаның көлденең және бойлық арқалықтары өске
симетриялы орналасқан. Бойлық арқалықтың жұптары айналы бетте және
параллельді сөрелі швейлермен горизонтальды бағыттаушы ретінде
құрастырылған ортаңғы бойлық арқалық өзара қима пішіні кернегішімен, бойлық
арқалықтың сонымен көлденең түйіндесулермен, үшкілдермен және түйіскен.
Бойлық арқалықтардың вертикальды сөрелеріндегі топсалы байланыс, осымен
кронштейін бекітілген.

1.4-сурет
Жоғарыда айтқан жүк көтеркіштің кемшілігі жоғары материялсиымдылық
және жоғары айырмашылығы корпус негізгі топсамен байланысқан, ал соташық
топсалы иінтірекпен, негізінен қозғалыссыз бекітілген, сонымен қатар
бекітілген нүкте иінтіректердің соңында орнатылған [7] (1.5 сурет).

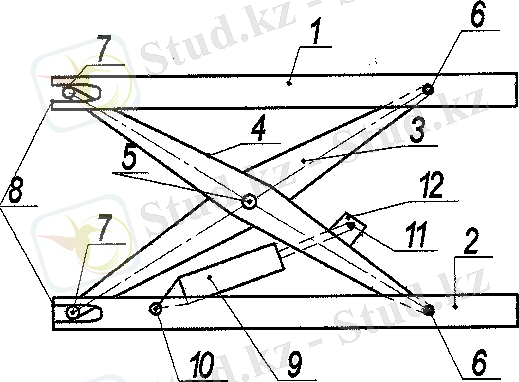
1.5 сурет

Тағы бір айырмашылығы цилиндр сот ашық консол арқылы иінтірекпен
байланысқан, платформа консолді байланыстыратын топса. иінтіректің бойлық
өсінің үстінде орналасқан.
Жоғарыда жазылған жүк көтергіш үстелдің кемшілігі эксплуациялық
сенімділігі төмен және бағасы қымбат.
1.6-суретте тағы бір жүк көтергіштің кинематикалық схемасы көрсетілген
[2]. Жүк көтергіштегі келтіру білігі – түрінде қозғалмалы келтіру жасалған,
жұлдызшалармен құрастырылған және төлкелі аумақша тізбектері иінтіректің
жұптарын қиып өтетін топсалы байланысқан өстермен еркін айналып тұратын
жұлдызшалар арқылы тармақталып байланысқан төлкелі – аумақшаның соңғы
тармақтары серпімді элементтермен байланысқан. Мысалы керілетін созылмалы
серіппе.

1.6 сурет
Жүк көтергіштің кемшілігі, эксплуатациялық сенімділігі төмен және
материалсиымдылығы жоғары.

1.7 сурет
1.7 суреттегі жүк көтергіш, негізінде қозғалмалы механизм орнатылған әр
элемех Х - бейнелі тор түрінде орындалған [4]. Келтіру механизмі элементтің
структуралық торларымен полиспас түрінде байланыс жасаған иілгіш элемент
бір соңы келтіру механизмнің барабаннан, ал екінші жағы –негізге
бекітілген.
1.8 суретте басқа бір жүк көтергіш көрсетілген қозғалмалы топса
элементтері орнатылған екі негізден тұрады [5]. Пантограф торы түрінде
салынып жасалған және келтіру элемент торымен байланысқан полисплат түрінде
негізге бекітілген. Иілгіш элемент бірінші аймақта келтіру элементінің
барабанында бекітілген бір негізге бекітілген, ал қозғалмалы элементтер V-
бейнесі конструкция түрінде орнатылған әрбіреуі төрт сырықты элементтен
тұратын, жалпы өске екі-екіден орнатылған, және де әр өсте полиспас
блоктары орнатылған, ал иілгіш элементтің екінші соңы екінші негізге
бекітілген. Бар аналогтардан айырмашылығы иілгіш элемент арқан және тізбек
түрінде жасалған, келтірудің барабан элемент қозғалтқышпен және қолмен
келтіріледі.

1.8 сурет
Суреттелген жүк көтергіштің кемшілігі конструкциясы қиындығы,
материялсиымдылығы үлкен және техникалық қызымет ету қиындығы.
1.9-суретте көтеру – транспорттық машина жасауға жататын тағы жүк
көтергіш құрылған [6].
Жүк көтергіш үстел негізден қозғалмалы платформадан және көтеретін
келтіруден тұрады. Негізінің топсалар тіреулері және қосымша иінтіректер
негізінің шетінде және қозғалмалы платформадан бекітілген.
Көтеретін келтіру қысқа және ұзын өсті негізгі және қосымша жұптар
және дағы гидроцилиндрлі айқасқан иінтіректі топсалы түрінде орналастырып
құрастырылған.
Цилиндр негізнен ұзын өсті болып, ал екі иімді иінтірекпен байланысқан
соташықпен, қысқа өсті болып құрастырылған.

1.9 сурет

Қозғалмалы көтергіштің кемшілігі техникалық және эксплуациялық
сенімділігі төмен.
1.10 суретте жүк көтергіш берілген платформадан, арасында топсалы-
иінтіректі механизм орналасқан [7], иінтіректі қиып жатқан екі топсалы
байланысы бар, бір соңы бағыттауышқа құрастырылған платформа мен негізге
бекітілген, иінтіректің басқа жақтары байланысқан және гидроцилиндр жұбы
түрінде қозғалмалы келтіру, екі иінді иінтіректің соташықтар иінтіректі
қиып жатқын, бірінші гидроцилиндр негізгі бір иінтіректің төменгі соңғы
өсмен байланысқан. Негізінен топсалы байланысқан айырмашылығы, екінші
гидроцилиндр негізгі басқа иінтіректің төменгі соңғы өсімен байланысқан.

1.10 сурет

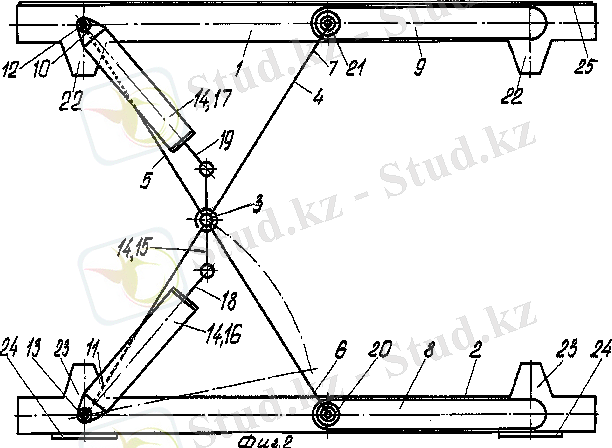
1.11 сурет
Айтылған жүк көтергіштегі шектелген, жоғары жағыдайда орнықсыз,
себебі консоль пішінді болып келеді.
1.12 суретте көрсетілген жүк көтергіш платформа және арасында
орналасқан топсалы-иінтіректі механизмнен тұрады [8]. Айтылған механизмдер
екі топсалы байланыс бар иінтіректі қиып өтетін бір соңы бағыттауышқа
құрастырылған платформаға бекітілген және негізге иінтіректің басқа
жақтарыда байланысқан және күш беруші гидроцилиндр жұбы түріндегі қозғалғыш
келтіру кіреді. Бірінші гидроцилиндр бір иінтіректің төменгі өсімен топсалы
байланысқан негізінен екінші гидроцилиндр басқа иінтіректің төменгі соңғы
өсімен байланысқан.
Жүк көтергіштің кемшілігі техникалық және эксплуатациялық сенімділігі
төмен, жүк көтергіш жоғарғы жағыдайда орнықты емес, себебі пішіні консольді
болып келеді.
1.12 суретте берілген жүк көтергіш платформада, иінтіректі жұп негізгі
бөлігі және жүк көтергіш платформа арасында орналасқан, әрқайсысында
иінтіректі қиып өтетін екі топсалы байланысы бар [9]. Бір жағы бағыттаушыға
құрастырылған, платформа негізгі жүйемен бекітілген иінтіректің басқа
жақтары топсалы байланысқан.

1.12 сурет
Иінтіректің топсаларының жұбы қарама-қарсы негізгі және платформаға
құрастырылған және көрсетілген механизмдердегі қозғалысқа келтіруге
кинематикалық байланысқан айырмашылығы, қозғалтып келтіруде, келтіру
белгісі, төлкелі аумақшаға арналған жұлдызшалар орнатылатын және
иінтіректің жұптарынан қиып өтетін топсалы байланысқан өстермен еркін
тармақталған байланысқан, төлкелі – аумақшаның соңғы тармақтары серпімді
элементтермен байланысқан. Мысалы керілетін созылмалы серіппе.
Бұл жүк көтергіштің кемшілігі техникалық эксплуатоциялық сенімділігі
төмен және қажет ету қйындығы.
1.13-суретте белгілі жүк көтергіш үстел қозғалмалы платформамен
берілген [10].
Платформа мен негізгі бөлігі өзара кинематикалық байланысқан және
қосымша жұптар Нюрнберг қайшысы түріндегі айқасқан иінтіректер топсалар
түйіндесуде айқасқан иінтіректерде және қосымша жұптар ұзын және қысқа өске
орнатылған. Қозғалмалы платформаның жүк көтергіш келтіруі күш беретін
цилиндр түрінде негізгі және қозғалмалы платформада орналасқан.

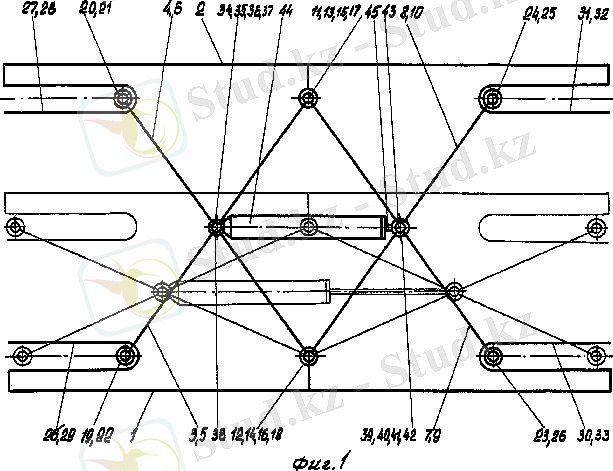
1.13 сурет

Көрсетілген цилиндр негізгі қысқа өстерге қарастырылған соташық (шток)
атталған цилиндр ұзын өспен байланысқан жүк көтергіш үстел аспаптың
орынауыстырумен бекіткішпен жабдықталған [11]. Көрсететінбекіткіш бір
корпус түрінде, ұзын өстерге бөлекту және арықарай бір түбі айқасқан
иінтіректің қосымша жұбының ұзын өсінде диаметрді тесігінде жіберілген.
Жоғарыда айтылған корпус конустық түрде болады. Сфералық денелер қисық
соташықтан радиальды арналарда корпуспен және арқанмен өзара әрекеттесіп
орнатылған
Берілген жүк көтергіштің үстелдің кемшілігі динамикалық теңдеулердің
айқастырылған иінтіректе төмендеуі біраз ғана емес, негіз және қозғалмалы
платформа.

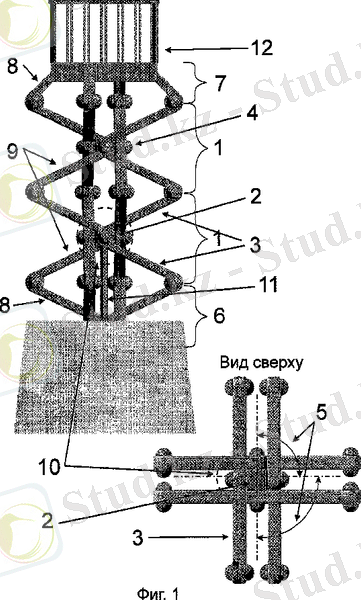
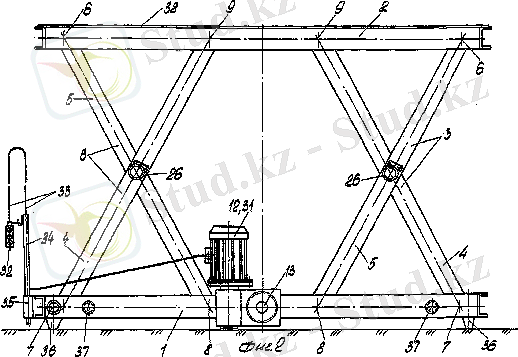
1.14 сурет
1.14-суреттегі жетекпен, беріліс бөлім және орындаушы бөлім тұрады.
Беріліс бөлімі түрінде орындалған, жоқ дегенде екі секциялық, әр
қайсысышоршорлы түйіннен түзіледі және онда иінтіректі айналу мүмкін
болатындай орнатылған. Топсаны түйін жоқ дегенде үш өстен және біліктен
тұрады, айналу өстері бір кеңістікте орналасқан, өстердің бұрышы бірдей.
өстердің саны әр түрлі топсалар түйіндерінде бір механизімде бірдей
иінтректер бірінші және соңғы секция құрамына кіретін бір иінде немесе екі
иінде орындалған. Басқа секция кіретін иінтіректен екі иінді әр бір иінді
иінтірек бір жағы айналу мүмкін болатындай өске не топсалы түйіннің
білігіне, ал басқа жағы топсалы шектес акцияға байланысқан. әрбір екі иінді
иінтіректен ортаңғы бөлігінде айналуға мүмкін болатын өске не топсалы
түйіннің білігіне орнатылған. Иінтірек бірінші секциядағы бір жағы топсалы
келесі секцияяның иінтірегіне, басқа жағы – жетекпен байланысқан соңғы
секциядан иінтірек топсамен алдыңғы секциямен, ал басқа секцияларға әрбір
иінтірек бір жағы алғашқы секциямен, ал басқа жағы алдыңғы секциямен
байланысқан. Бір секцияның иінтірегінің айналу бағыты шектес секцияларға
қарама-қарсы.

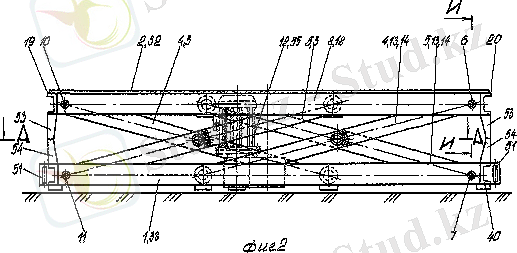
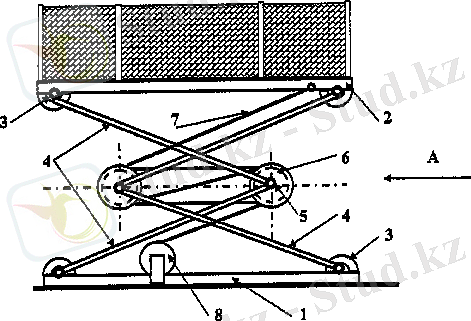
2 “Нюрнберг қайшысы” типті төменгі жетекті жүк көтергіш механизмдер
жетегін оптималдау

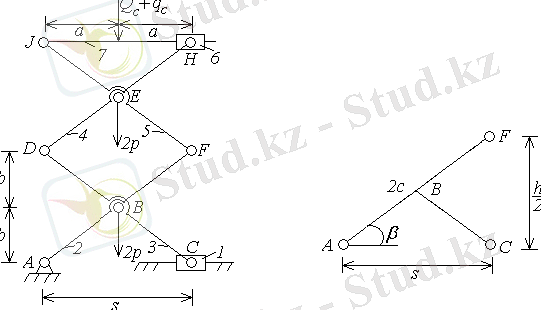
2.1,а суретте 7 платформасы бар жүк көтеруші механизмнің кинематикалық
сұлбасы және 1 кіріс буыны көрсетілген.“Нюрнберг қайшысы” атты дәстүрлі
механизмді төменгі жетекті сұлбасы атау қабылданған, сызықтық қозғалыстың С
сырғаның жалпыланған координатасы q=s; s=AС бар. Механизмнің кинематикалық
сұлбасы буындар ұзындығымен AF=FJ=CD=2c және платформаның көтерлу
биіктігімен h=AJ анықталады .

а) б)
2.1-сурет

Механизм кинематикасы өте қарапайым формулалармен анықталады.
Тікбұрышты 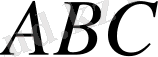үшбұрышынан (2.1, б -сурет)
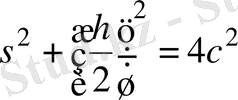(2.1)
Бұл өрнекті дифференциялдасақ
,
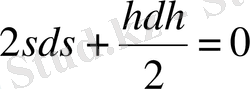Ендеше
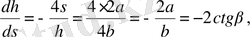
Мұндағы
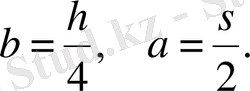
Айталық, Q және qс- сәйкесінше жүк және платформаның өз салмағы
болсын. Ал p – бір сырықтың салмағы. Онда теңгеріуші күш мына формуламен
анықталады:
, (2.2)
Мұндағы 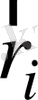- сыртқы күштердің әсер ету нүктелерінің радиусы –векторы,
- механизмге әсер ететін сыртқы күштер ретінде ауырлық күштерін ғана
қарастырамыз: .
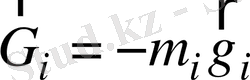Осыны есепке ала отырып 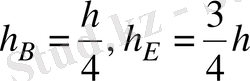, теңгеруші күш былай анықталады.
,
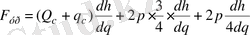яғни
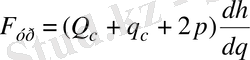. (2.3)
Бұған 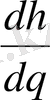мәнін қойып, аяғында керек өрнекті аламыз:
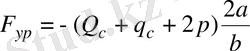аламыз (2.4)
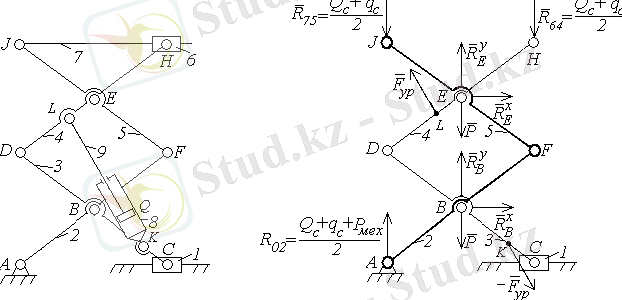
Енді топсалардағы реакцияларды анықтайық ( 2.2-сурет).

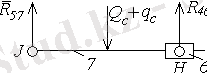
2.2-сурет
6-7 Ассура тобына әсер ететін реакцияларды анықтау үшін және
нүктелеріне сәйкес 6-7 буындардың моменттер теңдеуін жазайық.
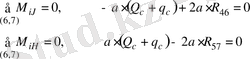(2.5)
Бұдан шығатыны
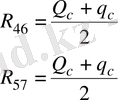. (2.6)
Енді екі сырықты 4-5 топты қарастырайық. 4 және 5 буындардағы
және топсаларына и , вертикал төмен бағытталған және
мәндері 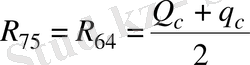рекциялар әсер етеді. Онда А және В топсаларының вертикал
құраушылары ( 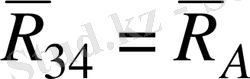и )
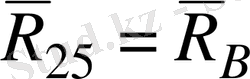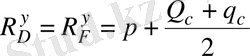. (2.7)
А горизонталь құраушылары С нүктесі бойынша 4 сырыққа әсер ететін
күштер моменттерінің қосындысының теңдеуін 0-ге теңестіру арқылы табамыз:
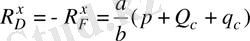(2.8)
4 сырықтағы күштер тепе-теңдігінің шартынан табамыз:
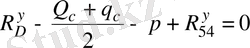, (2.9)
Бұдан: .
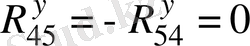(2.10)
2-3 Ассура топы үшін де ұқсас есептеулер жүргізіп (3,в-сурет),
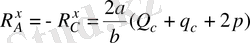(2.11)
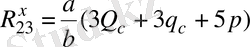(2.12)
болғанын табамыз

а) б)

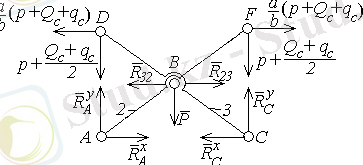
в)

2.3-сурет
Енді келесі сан мәндерін қойайық:
-жүк массасы (пайдалы жүктеме): кг (жүк салмағы Н);
- платформа массасы: кг (жүк көтеруші платформының салмағы
);
-бір сырықтың массасы: кг (сырықтың салмағы );
-сырықтың ұзындығы м.
Онда механизмнің төменгі күйінде (ерекше күйге жақын кезде) : 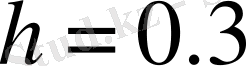м,
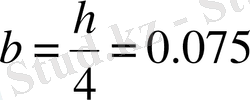м, м, теңгеруші күштің мәнін аламыз- 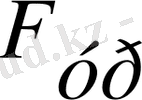= 47.024 кН, яғги 4798
кгС. Барлық нәтижелер 1-кестеге енгізілген.
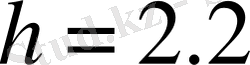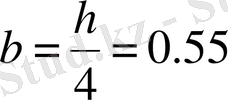Ал жоғары күйде, мұндағы м, м, м, теңгеруші күш -
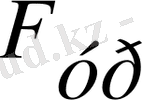= 3.068 кН, яғни. 313 кгС .
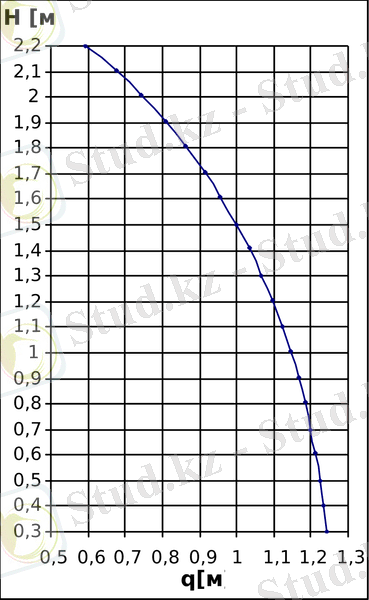
4, а- суретте 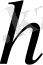=0,3м –ден 2,2м-ге дейінгі өзгеріс кезіндегі
платформаның көтерілу биіктігіне жалпылама координаттың тәуелділік
графигі көрсетілген.
Ал 4, б –суретте теңгеруші күштің платформаның көтерілу биіктігіне
тәуелділік графигі көрсетілген.

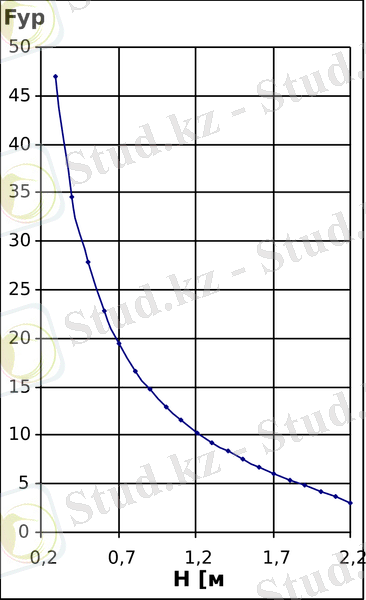
а) б)

2.4 –сурет (а) және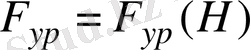(б) тәуелділіктерінің графиіктері.

2.1-кесте
№ h(м) s(м) β(град) Fyp (Н)
1. 0.3 1.24097 6.8921 47024.49
2. 0.40503 1.23349 9.32359 34620.43
3. 0.5005 1.22469 11.54871 27816.74
4. 0.60553 1.21278 14.01708 22768.29
5. 0.70101 1.19985 16.2842 19457.49
6. 0.80603 1.18325 18.80886 16688.2
7. 0.90151 1.1659 21.13723 14701.95
8. 1.00653 1.14421 23.74164 12922.99
9. 1.10201 1.122 26.15519 11574.21
10. 1.20704 1.09465 28.86936 10309.5
11. 1.30251 1.06694 31.39969 9312.001
12. 1.40754 1.03306 34.26457 8343.511
13. 1.50302 0.99887 36.95632 7554.892
14. 1.60804 0.95711 40.03205 6766.266
15. 1.70352 0.91488 42.95369 6105.215
16. 1.80854 0.86301 46.33733 5424.651
17. 1.90402 0.81005 49.60616 4836.424
18. 2.00905 0.74393 53.47701 4209.45
19. 2.10452 0.67472 57.33165 3644.64
20. 2.2 0.59372 61.64236 3067.913

(2.3) формула бойынша 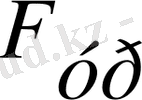шамасы 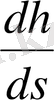өзгерісіне тәуелді, ол
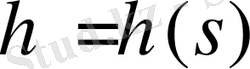графигіне жанама бұрышының тангенсіне тең. Төменгі күйде 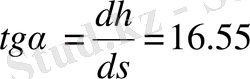. Онда
керек жүкті механизм сырықтарымен бірге көтеру үшін пайдалы жүктемеге
қарағанда 16.55 есе көп күш қажет. Бұл қарастырылып отырған механизмдегі
күштің берілуі тиімділктен өте алыс жатқандығын білдіреді. Сәйкесінше топса
реакциялардыңда төменгі күйде (ерекше күйге аса жақын 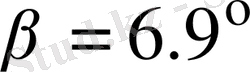) сан мәндері
аса жоғары. Бұл массасы 150кг жүкті көтеру үшін 4798 кгС тан аз емес күш
қажет деген сөз. Ал топсалардағы және 2 сырықтағы (кинематикалық
жұптардағы) үйкеліс күштерін жеңу үшін одан да көп күш қажет болады.

3. Тербелмелі гидроцилиндрлі жүк көтеруші механизмдердің күштік анализі

3.1. Күштік анализдің негізгі өрнектері
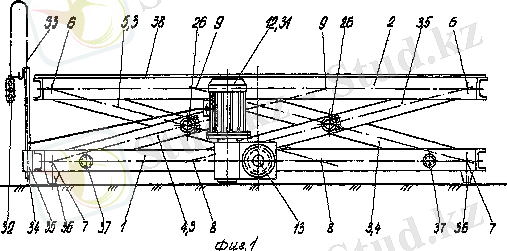
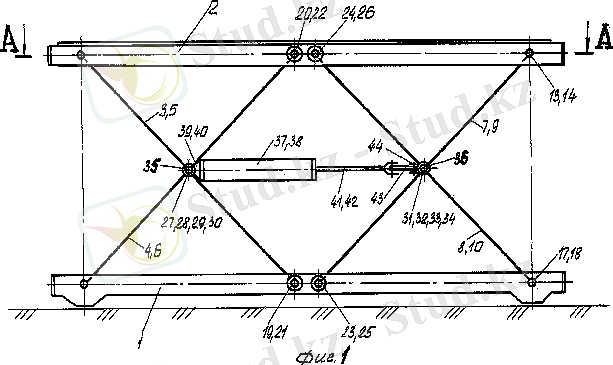
Қазіргі кезде өндірісте көп қолданылатын "Нюрнберг қайшылары"
конструкцияларында платформаның қозғалмалы буындарды гидроцилиндр мен
байланыстыратын жетек сұлбасы қолданылады.
3.1, а-суреттегі жетек сұлбасын қарастырайық, мұнда 8-9 гидроцилиндр 3
және 4 буындарын байланыстыр жетек сұлбасын ып тұр (кіріс кинематикалық
тізбек).

а) б)
3.1-сурет жетек сұлбасы

3.1.б-суреттерде көрініп тұрғандай, қозғалмалы сырықтардың
салыстырмалы қозғалысы берілген (ҚССБҚ), механизмдер түріне жатқызуға
болады. Біздің жағдайда 8 және 9 буындар. Сондықтан олардың күштік
анализінің реті әдеттегідей емес, Ассур тобының қабатталу ретыне кері
бағтталған. [2] рет бойынша тізбектей анализделінеді. Мұндай механизмдерді
Ассур тобына бөліп алуға болмайды. Осындай механизмдердің күштік анализдеу
нұсқаларын пайдалана отырып([2-5] жұмысында ұсынылған), анализді келесі
ретпен жүргіземіз.
Алдыңғы жағдайдағы сияқты, және шарнирлердегі реакция:

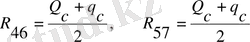(3.1)
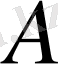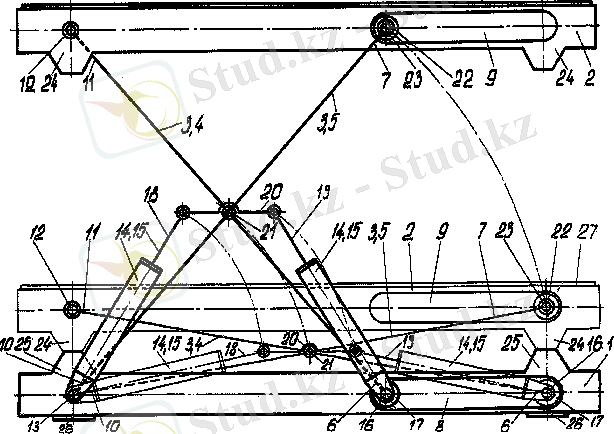
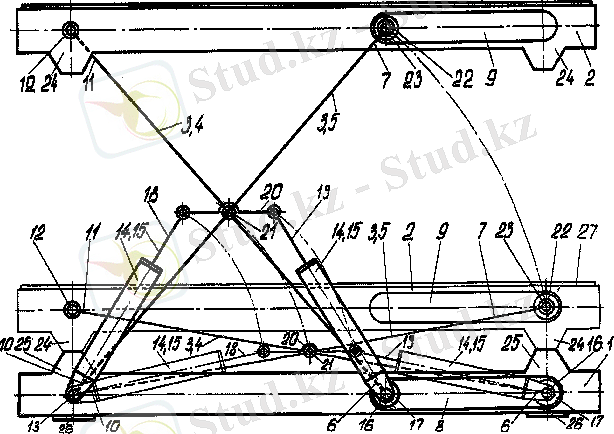
Ары қарай және топсаларына тірек жағынан әсер ететін
реакцияларды анықтайық. Ол үшін Ассурдың II кластық – УГА(1-У(2,3,4,5,6,7))
( 3.2-сурет) тобынан тұратын шартты механизмді есептейміз, мұндағы У –
шартты буын, 8-9 сырықтар қозғалысы фиксацияланған 2-3-4-5-6-7
сырықтарынан құралған.

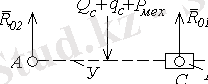
3.2-сурет

2-3-4-5-6-7 сырықтар тобы үшін және нүктелері бойынша
моменттер теңдеуін жазайық (шартты буынды құраушылар).

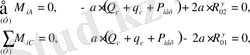(3.2)

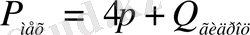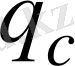мұндағы механизімнің жүк және платформа салмағынсыз
таза өз салмағы.
Іздеп отырған мәндерді анықтаймыз

(3.3)

Ары қарай кинематикалық тізбегін қарастырайық (2-5 сырықтар),
соның ішінде 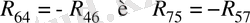. В нүктесі бойынша 2-5 сырықтардың моменттер теңдеуін
қолдана отырып
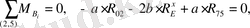(3.4)
бұдан
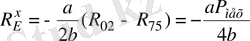. (3.5)
ОХ өсі бойынша күштердің тепе-теңдік теңдеуінен ,
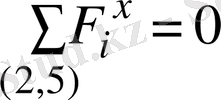
онда .

5 сырық үшін нүктесі бойынша моменттер теңдеуін жазайық:

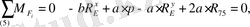(3.6)
бұдан .
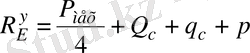2-5 жүйесі үшін ОY өсі бойынша күштердің тепе-теңдік теңдеуінен

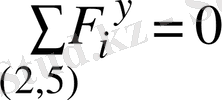
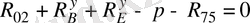(3.7)
.
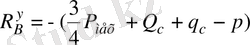Күштердің тепе-теңдік теңдеуінен жеке 5 сырық үшін

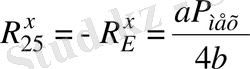. (3.8)
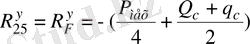. (3.9)
Енді теңгеруші күшті анықтаймыз, ол 4 сырықтың кинематикалық
жұбына түсірілген ( 3.3-сурет)

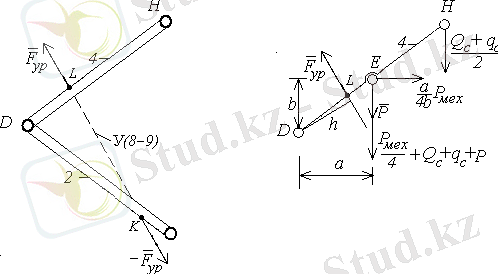
а) б)

3.3-сурет сырықтың кинематикалық жұбына түсірілген теңгеруші күшті

Ол үшін нүктесі бойынша 4 сырықтың моменттерінің тепе-теңдік
теңдеуін жазайық:
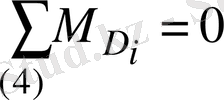, (3.10)
Ашық түрде :
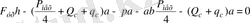(3.11)
Бұдан
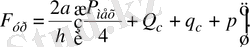(3.12)
Егер 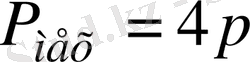, онда
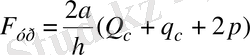, (3.13)
мұнадғы 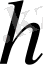ұшбұрыштан анықтаймыз: DK=1.106м, DL=0.205м болса,
платформа биіктігі 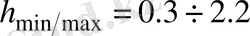шектерінде өзгеретін болса, онда KL ұзындығы мына
шекте өзгереді: 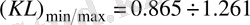м.

3.2.Айнымалыларды варияциялаудың ЛПτ–тізбектер әдісі

Гидроцилиндрдің шеткі K және L топсаларын әр түрлі сырықтарға бекіте
отырып, әр түрлі механизмдер алуға болады. Мысалы. K топсалы қозғалмалы O1
X1 Y1 координаттар жүйесіне қатаң бекітілген. Ал L топсалы O2 X2 Y2
координаттар жүйесіне қатаң бекітілген болсын. Осы аталған координаттар
жүйесіне қатысты жергілікті (локалды ) координаталарды деп
белгілейміз.

3.4-cурет Локалды координаттар жүйесінде гидроцилиндрдің шеткі
топсаларының орналасуы
Өзгеретін айнымалыларды өзгерту үшін 4-өлшемді кеңістіктегі
параметрлердің зондтау әдісі қолданылады. Қарастыратын әдістің ерекшелігі-
көп өлшемді областы жүйелі түрде қарау. Кеңістік параметрлерінде байқау
нүктелері ретінде біркелкі ретпен таралған нүктелер қолданылады. Осы
мақсатта біркелкі таралуы жағынан ең жақсы болған ЛПτ- тізбектер деген
белгілі әдіс қолданылады. Өз уақытында акедемик И.И.Артоболевский айтқандай
˝оптималды шешім іздеу дегеніміз ең алдымен есепті дұрыс қою˝. Бізге
белгілі, академик И.И.Артоболевский және Г.В.Крейнии осы әдісті
механизмдерді және машиналарды жобалау тәжірибесіне енгізуге көп ықпал
жасады. Осы әдісті жасауда И.М.Соболь және Р.Б.Статников көп еңбек сіңірген
[17].
Көп өлшемді облысты жүйелеп іздеуде ЛП- іздеу деп аталатын кеңістік
параметрлерді қарау әдісі қолданылады. ЛП-іздеу өте тиімді болатын 2 түрлі
есептер класын көрсетуге болады.
Біріншіден, бұл есептерде бір уақытта n-өлшемді кеңістікте берілген
бірнеше мақсат функцияларының бірнеше күштердің максмумын (немесе
минимумын) талдауға болады, себебі бірнеше функциялардың мәнін бағалау үшін
бірдей байқау нүктелеріндегі мәндері қолданылады. Екіншіден бұл есептер көп
экстремальді функциялардың глобальды экстремум іздеу үшін жергілікті
(локалды) оптимизациялау әдісі қолданылады; глобальді экстремумын іздеген
кезде локалды экстремумға түсіп кетпеу үшін әртүрлі бастапқы нүктелерден
бастап бірнеше рет локалды минимумды іздеу керек, сондықтан бастапқы
нүктелер Пn –де n-өлшемді параллелепипедте біркелкі орналасқан болу керек.
Бастапқы нүктелерді таңдауда ең тиімді әдіс – ЛПτ- тізбектер әдісі.
ЛПτ- тізбектер әдісін қысқаша айта кетсек. Көп өлшемді кубта іздеуді
сипаттау үшін бірыңғай n-өлшемді Kn кубты қарастырамыз, ондағы n декарттық
координаталармен x1,...,хn сипатталатын Р нүктесін қарастырамыз.
Р=(х1,...,хn), 0≤хj≤1, j=1,2, ... n теңсіздікті қанағаттандыру керек.
Осындай кубтың ішін біркелкі қарап шығу үшін кубты (3.5-сурет) , N=Mn
нүктеден тұратын торға бөлген ең дұрыс деп есептеледі.
Ол нүктенің координаталары , мұндағы
i1 , ... in әр қайсысы тәуелсіз түрде барлық 0,1, ... ,(M-1) мәндерін
қабылдайды. Бірақта бұл дұрыс емес. Мұндай тор n=1 болған жағдайда ғана
тиімді (3.6-сурет). n=2 болғанда жақсы емес, n өскен сайын бір қалыпылығы
тез төмендейді. Алғаш рет Kn –дағы кубтық тор – n үлкен болғанда
нашарторшалар құрайды деген тұжырым 1957 жылы шықты [17].
Бұл жағдайды нақтылау үшін, 3.5-суретте көрсетілген екі өлшемді торды
салыстырайық торламаны 3.6-суреттегі тор 16 нүктеден тұрады. 3.7-суретте
көрсетілген кездейсоқ ЛПτ – тізбектерінен құралған тормен алмастырайық.
Мұнда да 16 нүкте көрсетілген (яғни ЛПτ –тізбегінің 14 нүктесі
бейнеленген).

3.5-сурет n=2 болғандығы кубтық тор

Екі жағдайда да 16 торшаның әр қайсысында (кішкентай 16 квадраттар)
бір нүктеден ғана бар нүктелердің орналасуының біркелкілігі бірдей сияқты.
Бірақ мысалы мынадай жағдайда өзгешелік бірден білінеді. f(х1;х2)
функциясын зерттейтін, ол К2 (квадратта) анықталған болсын; бірақ бірінші
аргументіне қатты тәуелді болсын, мысалы f=f(х1). Бұл жағыдайда f
функциясының мәнін 1-ші торламаның нүктелерінде есептесек (3.6-сурет), онда
біз әртүрлі төрт-ақ мән аламыз, (әр қайсысы төрт рет қайталанылатыны); ал
3.8-суретегі торламаны пайдаланғанда f функциясын өзгерту диапазоны
жақсартады: 16 мән аламыз.

3.6-сурет n=1 (N=8) болғанда кубтық тор

3.7-сурет n=2 болғанда жақсартылған торлама (N=16) болғанда

Көп өлшемді жағдайда кубтық тор одан да нашарлайды, f(х1,...,хn)
есептегенде информацияның жоғалуы одан да өсуі мүмкін: f(х1)
функциясының N=Mn мәнін есептей отырып, біз M=N1n әртүрі мән аламыз.
Қарастырылған f(х1)- өте тиімсіз жолмен ескеріліп отыр, ал өмірде
f(х1,...,хn) функциясы барлық аргументтің ішінде бірнеше айнымалыға ғана
қатты тәуелді болады.
Мысалы, егер f(х1,...,хn) функциясы мынадай түрде болса
f (х1,...,хn)= g (хi1 ,...,хiM)+ h (х1,...,хn),
Мұндағы mn және gh. Бұндай формада жоғарыда айтылған информация
жоғалуы көрініп тұр: f функциясының N=Mn мәнін есептесек, біз Mm=Nmn
функциясының әртүрлі мәнін аламыз. Артық нүктелер саны N- Nmn, M өскенде
тез өсіп отырады; мысалы, егер n=5, m=3 және M=10, онда
N- Nmn =M5-M3=9900, ал жалпы саны N= M5=100000
Осыдан шығатыны тұжырым: Kn-дағы көпөлшеулі торламадағы нүктелердің
проекциялары "жақсы" болу үшін кубтың m-өлшемді жақтарында "жақсы" m-
өлшемді торлама шығуы керек жәнебұл тұжырым m=1,2,...n-1 әр кез-келген m
мәнінде дұрыс болу керек.
Сонымен қатар көп өлшемді кубта іздеу кезінде Kn-дағы біркелкі таралған
тізбектелген нүктелер ұғымы қолданылады. P1,...,Pi,...–Kn – де жататын
нүктелер тізбегі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.