Ақпараты толық емес техникалық жүйенің басқару заңын синтездеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ МЕН ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. Сәтбаев атындағы Қазақ ұлттық техникалық университеті
Автоматика және телемеханика кафедрасы
КУРСТЫҚ ЖҰМЫС
Тақырыбы Ақпараты толық емес техникалық жүйенің басқару заңын синтездеу
Алматы 2007
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. Сәтбаев атындағы Қазақ ұлттық техникалық университеті
Автоматика және басқару институты
Автоматика және телемеханика кафедрасы
Мамандығы 3601
Курстық жұмысты орындауға арналған
тапсырма
Студент Оспанов Бауыржан Әшімханұлы
Курстық жұмыстың тақырыбы Ақпараты толық емес техникалық жүйенің басқару заңын синтездеу
Аяқталған жұмысты тапсыру мерзімі
Жұмысты орындауға берілген бастапқы мәліметтер:
Варианттар бойынша: А -
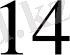 , b -
, b -
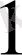 , c -
, c -
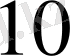 , s
*
, s
*
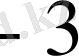 ;
;
A =
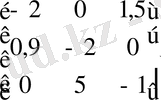
 матрицасы;
матрицасы;
 b=
b=
 - (
- (
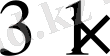 ) матрицасы;
) матрицасы;
c =
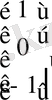 -
-
 матрицасы;
матрицасы;
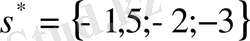
Есептеу түсініктеме хаттың мазмұны: 1 Теориялық бөлім 2 Есептеу бөлімі
Графикалық материалдардың тізімі (міндетті сызбалардың нақты көрсетілуімен:
(басқару заңдылығының
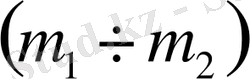 ,
,
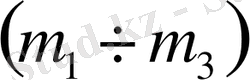 және
және
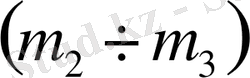 параметрлік жазықтықтарында орнықтылық ауданын D-бөліктеу әдісімен анықтау және Matlab ортасында моделдеу, толық қамтылған жүйенің
параметрлік жазықтықтарында орнықтылық ауданын D-бөліктеу әдісімен анықтау және Matlab ортасында моделдеу, толық қамтылған жүйенің
 қалып векторы және
қалып векторы және
 айнымалысы бойынша өтпелі процестерді құрастыру)
айнымалысы бойынша өтпелі процестерді құрастыру)
Негізгі әдебиеттер тізімі
Бегдуллаев К. Б. «Автоматизация исследования систем управления»,
Бегдуллаев К. Б. «Алгоритмы и программы расчета систем автоматического управления», Бегдуллаев К. Б. «Анализ и синтез систем автоматического управления методами пространства состояний».
Курстық жұмысты дайындау
графигі
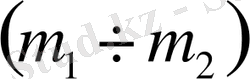 ,
,
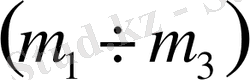 және
және
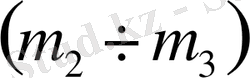 параметрлік жазықтықтарында орнықтылық ауданын D-бөліктеу әдісімен анықтау
параметрлік жазықтықтарында орнықтылық ауданын D-бөліктеу әдісімен анықтау
Берілген
 спектрді қамтамасыздындыратын
спектрді қамтамасыздындыратын
басқару заңын табу
 шығыс айнымалысын қолданып, бақылау құрылғысын синтездеу.
шығыс айнымалысын қолданып, бақылау құрылғысын синтездеу.
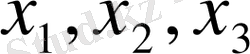 және
және
 айнымалылары бойынша өтпелі процестерді құрастыру
айнымалылары бойынша өтпелі процестерді құрастыру
Тапсырма берілген уақыт
Жобаның жетекшісі Бегдуллаев К. Б.
Тапсырманы орындауға алған студент Оспанов Б.
Мерзімі «» 2007 ж.
Мазмұны
Кіріспе . . . 7
1 Теориялық бөлім
1. 1 Техникалық жүйенің орнықтылығын Раусс таблицасы арқылы табу . . . 8
1. 2 Техникалық жүйесінің басқарулығын анықтау . . . 9
1. 3. Техникалық жүйесінің бақылаулығын анықтау . . . 9
1. 4 Техникалық жүйесінің фаза канондық формасына келтіретін L матрицасын анықтау . . . 10
1. 5 Техникалық жүйесінің басқару заңының коэффициенттерінің
,
және
жазықтығында орнықтылық ауданын
D-бөліктеу әдісімен анықтау . . . 11
1. 6 Техникалық жүйесінің берілген
 спектрді қамтамасыздындыратын
спектрді қамтамасыздындыратын
басқару заңын табу . . . 13
1. 7 Техникалық жүйесінің
шығыс айнымалысын қолданып, бақылау құрылғысын синтездеу . . . 15
1. 8 Синтезделген бақылау құрылғысын ақпарат толық емес техникалық жүйесінің басқару заңын синтездеуде қолдану . . . 16
1. 9 Толық қамтылған жүйенің
және
айнымалылары бойынша өтпелі процестерді құрастыру . . . 17
2 Есептеу бөлімі . . . 20
2. 1 Техникалық жүйенің орнықтылығын Раусс таблицасы арқылы табу . . . 20
2. 2 Техникалық жүйесінің басқарулығын анықтау . . . 21
2. 3. Техникалық жүйесінің бақылаулығын анықтау . . . 21
2. 4 Техникалық жүйесінің фаза канондық формасына келтіретін L матрицасын анықтау . . . 22
2. 5 Техникалық жүйесінің басқару заңының коэффициенттерінің
,
және
жазықтығында орнықтылық ауданын
D-бөліктеу әдісімен анықтау . . . 23
2. 5. 1 Раусс таблицалық сынымен техникалық жүйенің орнықтылығын анықтау . . . 29
2. 6 Техникалық жүйесінің берілген
 спектрді қамтамасыздындыратын
спектрді қамтамасыздындыратын
басқару заңын табу . . . 35
2. 7 Техникалық жүйесінің
шығыс айнымалысын қолданып, бақылау құрылғысын синтездеу . . . 37
2. 8 Синтезделген бақылау құрылғысын ақпарат толық емес техникалық жүйесінің басқару заңын синтездеуде қолдану . . . 38
2. 9 Толық қамтылған жүйенің
және
айнымалылары бойынша өтпелі процестерді құрастыру . . . 39
Қорытынды . . . 43 Әдебиеттер тізімі . . . 44
Қосымшалар . . . 45
Кіріспе
Соңғы жылдары күй кеңістігіне негізделген автоматты басқару теориясы кеңінен қолданыс тапты. Қазіргі заманға сай автоматты басқару теориясының негізгі ерекшеліктеріне болып мыналар саналады: объектінің күй жазықтығында дифференциалды басқару жүйесі ретінде жазылуы; анализ және синтездеу есебін шешу кезінде алгебралық әдістерді қолдану; процестерді уақыт аймағында көрсету. Бұл әдістер басқару жүйесін жобалау кезінде сапалы жаңа мүмкіншіліктерді береді. Мысалы, синтездеу есебін шешу кезінде басқару шарты жеткілікті ма және жеткілікті емес пе, сонымен қатар қажетті өлшегіштердің құрамын анықтайды. Қазіргі заманға сай автоматты басқару теориясы анализдеу және синтездеу есебін шешу үшін күй жазықтығының әдісін кеңінен қолданады. Бұл әдістерді қолдану ЭЕМ-де математикалық қамтамасыздандыруды дұрыс қолдануға мүмкіндік береді.
Тұрақты канон базалы бисызықты жүйелерді зерттеу.
Қазіргі уақытта бисызықты жүйелерді басқаруды зерттейтін көптеген әдістер бар. Олар зерттеудің қиындығына және әртүрлілігіне сонымен бірге оқырғы мақсатына қарай түсіндіріледі. Сызықты жүйелерді зарттеу әдістерінен айырмашылығы-бұл әдетте бисызықты жүйелердің анықталған класына қолданылады. Яғни бұлардан тас аз әсер етеді немесе жұмыс істеуге қабілетсіз болады. Мысалы, фазалы жазықтық әдісі екінші ретті бисызықты туындысы бар бисызықты жүйелерге арналға, бірақ та n
 з, онды әсері болмайды.
з, онды әсері болмайды.
Абсолютті тұрақты теориялар әдісіне кеңістік жағдайда Лапунов функциялары нда базаланса, ал жеке бөліктеррде аддитивті Попов функцияларында базаланып, бисызықты кіретін сызықты жүйелерде қолданылады, олар берілген секторда орналысады. Егер берілген секторды орналысады. Егер бисызықты аддитивсіз сызықты жйеде болса, онда секторлық жағдайда қанағаттандырмайды, сондықтан бұл әдісті қолдану қиындау долады. Егер де сызықты жүйеде фильтірлік қасиеттер болмаса, онда осы әдістің негізі жоғылады. Ляпуновтың тікелей әдісін бисызықты жүйелерді зерттеудегі әмбебап әдіс деуге болады, бірақ іс жүзінде қолдануды Ляпунов функциясына сәйкестік табу қиындатады.
Жоғарыда айтылғандай, әрбір әдіс жақсы жұмыс істейалады, егер бисызықты жүйедегі арнайы класс спицифакасы.
Енді бисызықты жүйе классын, яғни тұрақты матрицалык канондық базасы бар спецификасын қарастырамыз. Бисызықты жүйенің бұл класын зерттеуде канондық түрлендіру маңызды роль жүйені арнайы мүрге келтіріп, барынша зерттеу процессін жеңілдетеді.
Бисызықты жүйелерді канондық түрге түрлендіру.
Сызықты жүйенің тұрақтылығын зерттеу негізінде теңдеу жүйеcінің шығысын тұрақтылықты анослиздеуге қолайлы түрге түрлендіреміз. Түрлендурілер ішіндегі ең белгілісі Ляпунов түрлендіруін болып табылады.
Сызықты стационарлық жүйені қарастырайық.
Х=А(t) (1)
х
 R, t
R, t
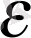 Equation. 3 I, I=
Equation. 3 I, I=
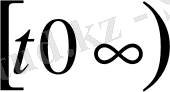 Equation. 3
Equation. 3
сызықты түрлендіру х=
 (t) y; (2)
(t) y; (2)
 Equation. 3 Ляпунов түрлендіруі, егер матрицалар
Equation. 3 Ляпунов түрлендіруі, егер матрицалар
 ,
,
 ,
,
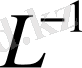 үзіліссіз (
үзіліссіз (
 үшін үздіксіз бөлінді жеткілікті
үшін үздіксіз бөлінді жеткілікті
Және барлық жарты осьтен шектелген
 :
:
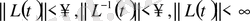
Бұндай түрлендіру
 жүйеде келесідей болады
жүйеде келесідей болады
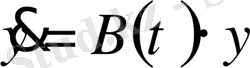 , (3)
, (3)
Яғни
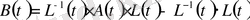
Егер матрица
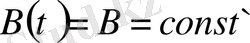 , онда
, онда
 жүйе.
жүйе.
1 Теориялық бөлім
1. 1 Техникалық жүйесінің орнықтылығын Раусс таблицалық сынымен анықтау
Раусстың орнықтылық сыны сипаттамалық теңдеудің коэффициенттері арқылы орнықтылық шартын көрсетеді. Көп жағдайда басқару теориясында келесі түрдегі сипаттамалық теңдеу қолданылады:
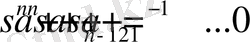 (1. 1. 1)
(1. 1. 1)
Раусс матрицасының бірінші элементі әрқашан тұрақты болады:

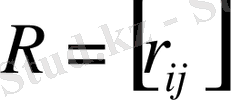
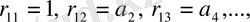 (1. 1. 2)
(1. 1. 2)
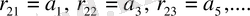
Раусс матрицасының бірінші жолы индексі жұп теңдеудің коэффициенттерінен тұрады, ал екінші жолы - индексі тақ коэффициенттерінен тұрады. Қалған элементтер келесі формулаларымен анықталады:
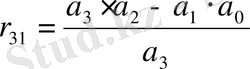 ;
;
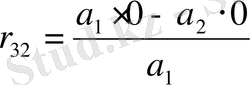 ;
;
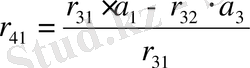 ; (1. 1. 3)
; (1. 1. 3)
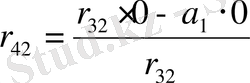
Раусс матрицасы
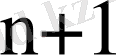 жолдан және
n
тақ болса
жолдан және
n
тақ болса
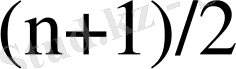 бағаннан, ал
n
жұп болған жағдайда
бағаннан, ал
n
жұп болған жағдайда
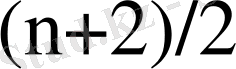 бағаннан тұрады. Раусс критерийі: жүйе асимптотикалық орнықты болу үшін, Раусс матрицасының бірінші бағананың элементтерінің оң болуы қажетті және жеткілікті.
бағаннан тұрады. Раусс критерийі: жүйе асимптотикалық орнықты болу үшін, Раусс матрицасының бірінші бағананың элементтерінің оң болуы қажетті және жеткілікті.
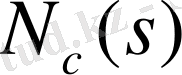 характеристикалық полиномның нақты бөлігі оң түбірдің саны Раусс таблицасының бірінші тік жолындағы элементтердің таңба өзгеру санына тең.
характеристикалық полиномның нақты бөлігі оң түбірдің саны Раусс таблицасының бірінші тік жолындағы элементтердің таңба өзгеру санына тең.
1. 2 Техникалық жүйесінің басқарулығын анықтау
Басқарулық ретінде Х күй кеңістігінің кез-келген нүктесінен координат басына өте алу қасиетін алуға болады. Егер әрбір күй басқарылатын болса, жүйе толығымен басқарылады деуге болады.
Басқарудың негізгі мақсаты, объектіге қойылатын нақты жұмыс істеу шарттары талап ететін басқарылатын объектінің динамикасын өзгерту. Мұндай өзгеру басқару жүйесінің теңдеуіндегі лайықты u басқару векторын анықтауымен жүзеге асады:
 (1. 2. 1)
(1. 2. 1)
Мұндағы
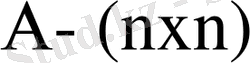 техникалық жүйені сипаттайтын матрица
техникалық жүйені сипаттайтын матрица
скалярлық басқарудың әсерін көрсететін вектор
техникалық жүйенің айнымалы күйлер векторы
- скалярлық басқару
 ;
;
Р. Калманмен басқарулық критериі дәлелденген. Ол бойынша жүйе толығымен басқарылу болу үшін Калман басқарулық матрицасының К с рангі n-ге тең болу керек:
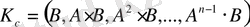 (1. 2. 2)
(1. 2. 2)
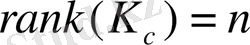
1. 3 Техникалық жүйесінің бақылаулығын анықтау
Келесідей техникалық жүйе берілсін:
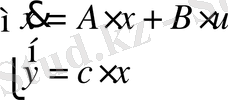 (1. 3. 1)
(1. 3. 1)
Мұндағы y - шығыс айнымалылар векторы
С - бақылау матрицасы
Калман бақылаулық сыны бойынша автоматты басқару жүйесі толық бақылаулы болу үшін оның Калман бақылаулық матрицасының рангі n-ге тең болу керек.
Мұнда Калман бақылаулық матрицасы дегеніміз:
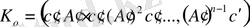 (1. 3. 2)
(1. 3. 2)
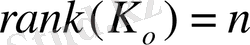
1. 4 Техникалық жүйесінің фаза канондық формасына келтіретін L матрицасын анықтау
Берілген техникалық жүйеміз келесідей теңдеумен сипатталады:
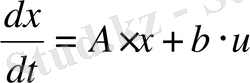 . (1. 4. 1)
. (1. 4. 1)
Бұл төмендегі басқару заңымен тұйықталсын:
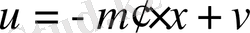 , (1. 4. 2)
, (1. 4. 2)
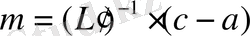 . (1. 4. 3)
. (1. 4. 3)
Мұндағы а мен с келесі сипаттамалық полиномдардың коэффициенттер векторлары:
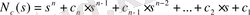 (1. 4. 4)
(1. 4. 4)
 (1. 4. 5)
(1. 4. 5)
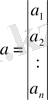 -
-
 ,
,
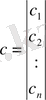 -
-
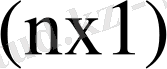
Ал L - фазалық канондық түрге түрлендіру матрицасы.
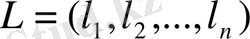 (1. 4. 6)
(1. 4. 6)
l
i
-
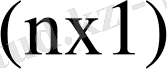
L матрицасының құраушыларын есептеу формуласы келесідей:
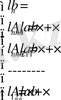
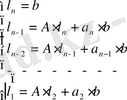 (1. 4. 7)
(1. 4. 7)
Біздің курстық жұмыста

L
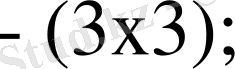
L
= (
l
1
, l
2
, l
3
)
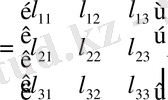
l
i
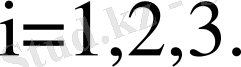
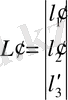
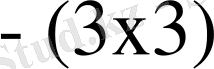
1. 5 Техникалық жүйенің басқару заңының коэффициентерінің
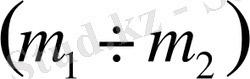 ,
,
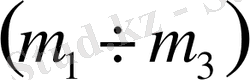 және
және
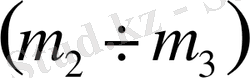 параметрлік жазықтықтарында орнықтылық ауданың D-бөліктеу әдісімен анықтау
параметрлік жазықтықтарында орнықтылық ауданың D-бөліктеу әдісімен анықтау
Алдыңғы бөлімнен бізге белгілі L матрицасын тауып алдық:
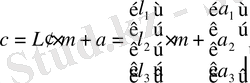
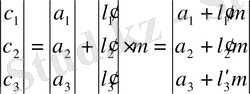
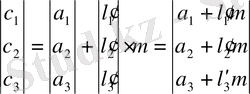
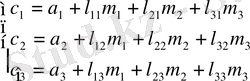 (1. 5. 1)
(1. 5. 1)
 деп алып, (
деп алып, (
 ) параметрлік жазықтығын қарастырайық.
) параметрлік жазықтығын қарастырайық.
Теңдеулер жүйесіндегі с 1 , с 2 және с 3 -ті теңдеуге қоямыз.
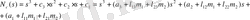 (1. 5. 2)
(1. 5. 2)
s
- тың орнына
j
 - ны қойып, теңдеуді нөлге теңестіреміз.
- ны қойып, теңдеуді нөлге теңестіреміз.
 (1. 5. 3)
(1. 5. 3)
Осыдан нақты және жорамал бөліктерін бөліп аламыз:
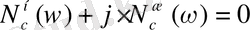
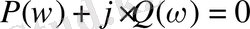 (1. 5. 4)
(1. 5. 4)
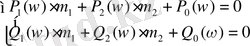 (1. 5. 5)
(1. 5. 5)
Осы теңдеулер жүйесін шешу үшін, Крамер ережесін қолданамыз:
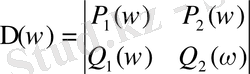 (1. 5. 6)
(1. 5. 6)
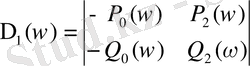 (1. 5. 7)
(1. 5. 7)
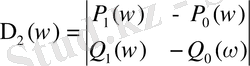 (1. 5. 8)
(1. 5. 8)
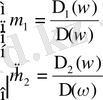 (1. 5. 9)
(1. 5. 9)
w=0 болғанда, m 1 , m 2 - ны келесі формулалар бойынша есептейміз.
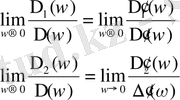 (1. 5. 10)
(1. 5. 10)
Түзу сызықтың теңдеуі:

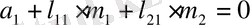 (1. 5. 11)
(1. 5. 11)
 =0
нүктесінде қисық түзу мен түзү сызық қиылысу керек.
=0
нүктесінде қисық түзу мен түзү сызық қиылысу керек.
Енді
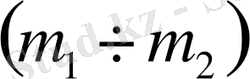 жазықтығында D-бөліктеудің қисығын сызып, тұйықталған жүйенің орнықтылық аудандарын табуға болады. Егер де кемінде бір ғана осындай аудан табылса, онда есеп шешілді. Егер де мұндай аудан жоқ болса, онда тұйықталған жүйені орнықтылықпен қамтамасыздандыратын басқару заңы жоқ.
жазықтығында D-бөліктеудің қисығын сызып, тұйықталған жүйенің орнықтылық аудандарын табуға болады. Егер де кемінде бір ғана осындай аудан табылса, онда есеп шешілді. Егер де мұндай аудан жоқ болса, онда тұйықталған жүйені орнықтылықпен қамтамасыздандыратын басқару заңы жоқ.
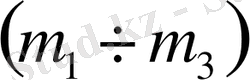 және
және
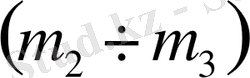 параметрлік жазықтықтары үшін есептеуді жоғарыда жасалған есептеулер бойынша жасаймыз.
параметрлік жазықтықтары үшін есептеуді жоғарыда жасалған есептеулер бойынша жасаймыз.
1. 6 Техникалық жүйенің берілген
 спектрді қамтамасыздандыратын басқару заңын табу
спектрді қамтамасыздандыратын басқару заңын табу
Сызықты стационарлы жүйені басқаруды қарастырайық:
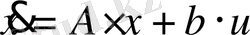 (1. 6. 1)
(1. 6. 1)
Басқару заңы келесі түрде алынсын:
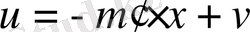 (1. 6. 2)
(1. 6. 2)
мұндағы:
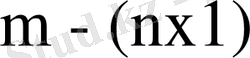 вектор
вектор
v - қосымша сигнал
А матрицасының характеристикалық полиномы:
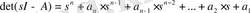 Equation. 3 (1. 6. 3)
Equation. 3 (1. 6. 3)
Белгісіз m векторын келесі формула бойынша табамыз:
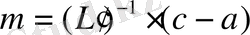 (1. 6. 4)
(1. 6. 4)
мұндағы: L - (nxn) түрлендіру матрицасы. Оны векторлар жиыны түрінде көрсетеміз:
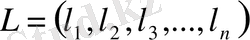 (1. 6. 5)
(1. 6. 5)
мұндағы: l - (nx1) вектор
l i векторларды мынадай рекурсия алгоритмімен табамыз:
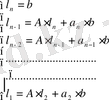 (1. 6. 6)
(1. 6. 6)
Есептеулердің дұрыстығын тексеру үшін келесі қатынас қолданылады:
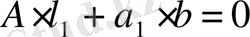 (1. 6. 7)
(1. 6. 7)
Яғни, егер де барлық l i дұрыс табылса (n+1) қатынасы нольдік векторға айналуы керек.
С матрицасының характеристикалық полиномының коэффициенттерін табу үшін берілген спектрді қолданамыз:
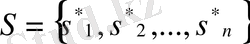
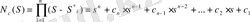 (1. 6. 8)
(1. 6. 8)
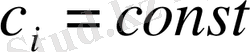 ,
,
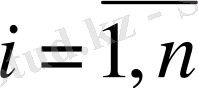
Объектіні басқару заңымен тұйықтағанда басқару заңымен қамтылған жүйеге келеміз:
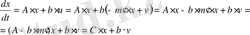
 (1. 6. 9)
(1. 6. 9)
мұндағы: С - (nxn) қамтылған жүйенің ақпарат толық кезіндегі матрицасы. Ол келесі характеристикалық полиномға ие:
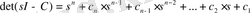 (1. 6. 10)
(1. 6. 10)
Есептеулердің дұрыстығын тексеру үшін келесі теңдікті қолданамыз:
 (1. 6. 11)
(1. 6. 11)
1. 7 Техникалық жүйесінің
шығыс айнымалысын қолданып, бақылау құрылғысын синтездеу.
Егер параметрлер жазықтығында ең болмағанда бір орнықты аудан табылса, онда басқарудың орнықты емес объекті келесі басқару заңдылығымен тұрақталуы мүмкін:
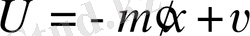 . (1. 7. 1)
. (1. 7. 1)
Бұл Р к реттеу кеңістігінде анықталады. Егер параметрлер жазықтығында ешқандай орнықты аудан болмаса, онда бұл Р к реттеу кеңістігі орнықты емес объектіні тұрақтауға жеткіліксіз дегенді білдіреді. Бұл жағдайда бақылау құрылғысын қолдануға тура келеді. Ол вектор компоненттерінің бағасын алуға және осылай реттеудің кеңістігінің өлшемін үлкейтуге мүмкіндік береді. Шығыс айнымалы жүйесі үшін теңдеу мына түрде болады:
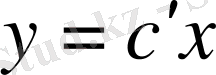 . (1. 7. 2)
. (1. 7. 2)
Бұл жерде с матрицасының бір элементі нолдік емес
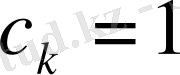 , ал қалған элементтері нолдік. Келесі теңдеумен сипатталатын бақылау құрылғысын құрайық:
, ал қалған элементтері нолдік. Келесі теңдеумен сипатталатын бақылау құрылғысын құрайық:
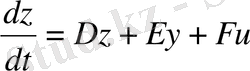 (1. 7. 3)
(1. 7. 3)
 (1. 7. 4)
(1. 7. 4)
мұндағы
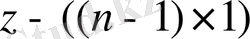 - бақылау құрылғысының күйлер векторы;
- бақылау құрылғысының күйлер векторы;
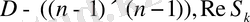 <0,
<0,
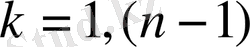 ;
;
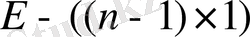 ;
;
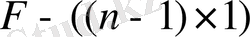 - тұрақты матрицалар. Бақылау құрылғысының матрицалық параметрлері келесі теңдеулермен анықталады:
- тұрақты матрицалар. Бақылау құрылғысының матрицалық параметрлері келесі теңдеулермен анықталады:
 (1. 7. 5)
(1. 7. 5)
 (1. 7. 6)
(1. 7. 6)
Бақылау құрылғысын қолданған басқару заңының синтезінде теңдеудегі басқару заңдылығына х күйлер векторының орнына оның бағалауын алсақ, тұйықталған жүйенің орнықтылығы бұзылмайды. Күйлер векторының бағалауын келесі әдіспен алуға болады. Бақылау құрылғысының күйлер векторы үшін және басқару объектінің шығыс векторы үшін теңдеу қарастырайық:
(1. 7. 8)
(1. 7. 7)
Бұларды блок түрінде жазуға болады:
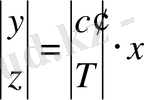 (1. 7. 9)
(1. 7. 9)
Егер бұл жүйенің матрицасының толық рангі болса, онда бағалау векторы келесі түрде болады:
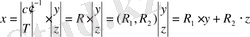 (1. 7. 10)
(1. 7. 10)
1. 8 Синтезделген бақылау құрылғысын ақпарат толық емес техникалық жүйесінің басқару заңын синтездеуде қолдану
Алдыңғы бөлімде тауып алған
 қолдана отырып ақпарат толық емес кезіндегі синтезделген заңын аламыз:
қолдана отырып ақпарат толық емес кезіндегі синтезделген заңын аламыз:
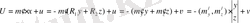 (1. 8. 1)
(1. 8. 1)
Осы жоғарыдағы жасаған алгоритмнің дұрыстығын тексеру үшін келесідей есептеулер жүргізіледі:
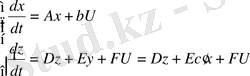 (1. 8. 2)
(1. 8. 2)
 (1. 8. 3)
(1. 8. 3)
 (1. 8. 4)
(1. 8. 4)
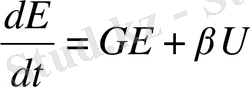 (1. 8. 5)
(1. 8. 5)
мұндағы
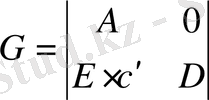 - (5х5) өлшемді матрицасы
- (5х5) өлшемді матрицасы
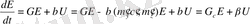
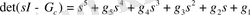 (1. 8. 6)
(1. 8. 6)
(1. 8. 6) полиномының түбірлері
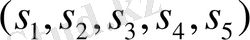 . Мұнда
. Мұнда
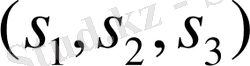 бастапқы мәліметтерде берілген
бастапқы мәліметтерде берілген
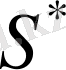 спектірімен сәйкес келеді және
спектірімен сәйкес келеді және
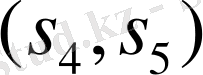 D матрицасының түбірлері.
D матрицасының түбірлері.
1. 9 Толық қамтылған жүйенің
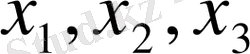 және
және
 айнымалылары бойынша өтпелі процестерді құрастыру
айнымалылары бойынша өтпелі процестерді құрастыру
Сызықты басқару жүйесін қарастырайық:
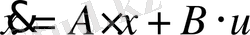 (1. 9. 1)
(1. 9. 1)
мұндағы
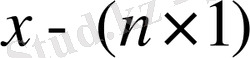 -айнымалы күй векторы,
-айнымалы күй векторы,
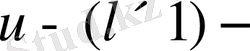 басқару векторы;
басқару векторы;
А, В-сәйкес өлшемді тұрақты матрицалар.
(6. 1) жүйесіне келесі беріліс функциясы сәйкес келеді:
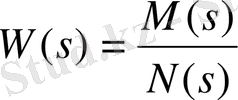 (1. 9. 2)
(1. 9. 2)
Мұндағы
(1. 9. 3)
теңдеуінің түбірлері беріліс функциясының полюстары деп аталады. Ал
(1. 9. 4)
Мұндағы
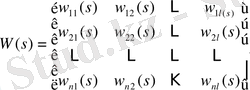 (1. 9. 5)
(1. 9. 5)
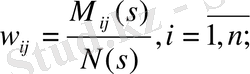
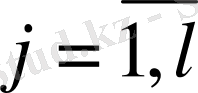
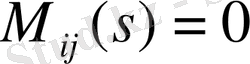 болған кездегі түбірлер беріліс функциясының нолдері деп аталады. Нолдер мен полюстердің комплексті жазықтықта орналасуын жүйенің динамикалық сипаттамаларын анықтайды. Бұл байланысты х
к
-қа қатысты жүйенің өтпелі сипаттамаларын жазсақ байқауға болады.
болған кездегі түбірлер беріліс функциясының нолдері деп аталады. Нолдер мен полюстердің комплексті жазықтықта орналасуын жүйенің динамикалық сипаттамаларын анықтайды. Бұл байланысты х
к
-қа қатысты жүйенің өтпелі сипаттамаларын жазсақ байқауға болады.
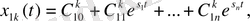
(1. 9. 6)
. . .
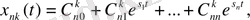
мұндағы
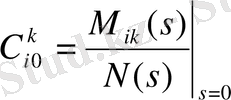 (1. 9. 7)
(1. 9. 7)
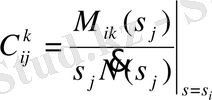 ,
,
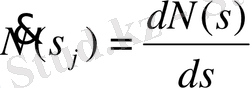 ; (1. 9. 8)
; (1. 9. 8)
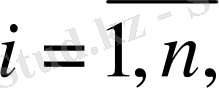
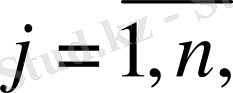
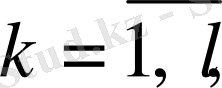
Нөлдер мен полюстердің комплексті жазықтықта орналасуы жүйенің динамикалық сипаттамаларын анықтайды. Бұл байланысты у теникалық жүйенің шығысына қатысты жүйенің өтпелі сипаттамаларын жазсақ байқауға болады.
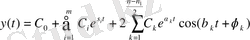 (1. 9. 9)
(1. 9. 9)
мұндағы,
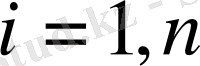 полиномның нақты түбірлері.
полиномның нақты түбірлері.
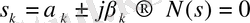 комплексті түбірлерінің жұптары.
комплексті түбірлерінің жұптары.
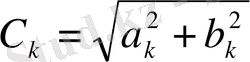 ,
,
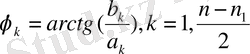 (1. 9. 10)
(1. 9. 10)
Сонымен өтпелі процестің түрі жүйенің полюстары мен нолдері арқылы анықталады. Егер беріліс функциясының нолдері болмаса, онда өтпелі процестің түрі комплекс жазықтығында сәйкес облыстарға орналастыруға болатын тек полюстармен анықталады. Мұндай жүйелер үшін басқару заңдылығын синтездеу кезінде тұйықталған жүйедегі берілген сапасы бар өтпелі процестерді қамтамасыз ететін арнайы стандартты
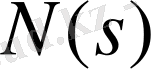 характистикалық полиномдарын қолданған ыңғайлы.
характистикалық полиномдарын қолданған ыңғайлы.
2 Есептеу бөлімі
2. 1 Техникалық жүйесінің орнықтылығын Раусс таблицасы арқылы табу
Алдымен объектінің орнықтылығын анықтау үшін (1. 1. 1) түрдегі теңдеуді аламыз:
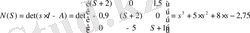
Ары қарай (1. 1. 2), (1. 1. 3) формулаларына сүйеніп Раусс кестесінің элементтерін тауып, кестені толтырайық:
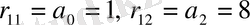
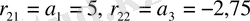
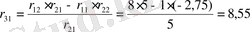
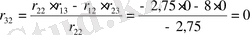
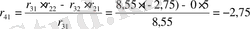
Кесте 2. 2. 1
Раусс кестесінің бірінші бағана элементтері ережеге сәйкес келмегендіктен, біздің техникалық жүйеміз асимтотикалық орнықсыз деген тұжырымға келеміз.
2. 2 Техникалық жүйенің басқарулығын анықтау
Объектінің басқарулығын анықтау үшін алдымен Калман басқарулық матрицасын (1. 2. 2) формула арқылы есептейік. Біздің курстық жұмысында n =3, сондықтан біздің Калман басқарулық матрицасы келесідей болады:
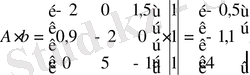 ,
,
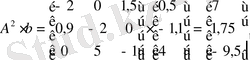 ,
,
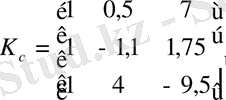
Объект басқарулы болу үшін
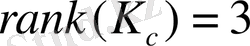 болу керек.
болу керек.
 матрицасы квадратты болғандықтан
матрицасы квадратты болғандықтан
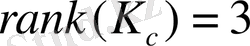 болу үшін матрицаның детерминанты 0-ге тең емес болуы қажет.
болу үшін матрицаның детерминанты 0-ге тең емес болуы қажет.
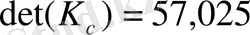 .
.
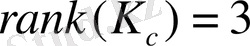 болды, сондықтан біздің объекті басқарылады.
болды, сондықтан біздің объекті басқарылады.
2. 3 Техникалық жүйенің бақылаулығын анықтау
Енді объекті бақыланатын болу үшін (1. 3. 4) формулаға сәйкес
 матрицасын тауып, ол матрицаның
матрицасын тауып, ол матрицаның
 болу керек.
болу керек.
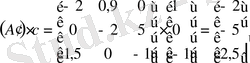 ,
,
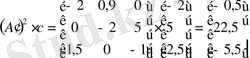 ,
,
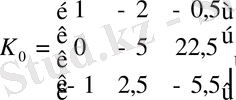
Объект басқарулы болу үшін
 болу керек.
болу керек.
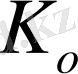 матрицасы квадратты болғандықтан
матрицасы квадратты болғандықтан
 болу үшін матрицаның детерминанты 0-ге тең емес болуы қажет.
болу үшін матрицаның детерминанты 0-ге тең емес болуы қажет.
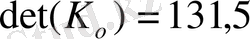 .
.
Жоғарыда жасалы
 нған есептеулер бойынша
нған есептеулер бойынша
 тең болды, сондықтан біздің объекті бақыланады.
тең болды, сондықтан біздің объекті бақыланады.
2. 4 Техникалық жүйенің фаза канондық формасына келтіретін L матрицасын анықтау
Алдымен (1. 4. 6), (1. 4. 7) формулаларына сәйкес L түрлендіру матрицасын табайық.
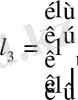 ,
,
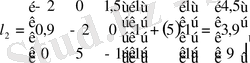 ,
,
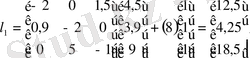 ,
,

Енді L түрлендіру матрицасының дұрыстығын тексерейік, ол үшін келесі теңдік орындалу керек:
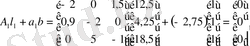
Қойылған шарт орындалғандықтан L түрлендіру матрицасы дұрыс екенін көреміз.
2. 5 Техникалық жүйенің басқару заңының коэффициенттерінің
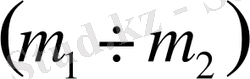 ,
,
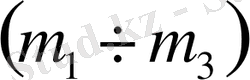 және
және
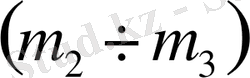 жазықтықтарында орнықтылық ауданың D-бөліктеу әдісімен анықтау
жазықтықтарында орнықтылық ауданың D-бөліктеу әдісімен анықтау
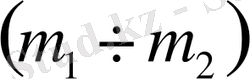 параметрлік жазықтығында D-бөліктеу әдісімен орнықтылық ауданың анықтайық. Біздің
А
матрицасының (1. 5. 5) полиномы келесідей болады:
параметрлік жазықтығында D-бөліктеу әдісімен орнықтылық ауданың анықтайық. Біздің
А
матрицасының (1. 5. 5) полиномы келесідей болады:
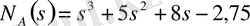
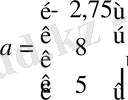 - коэффициенттер векторы.
- коэффициенттер векторы.
Алдымен (1. 5. 8) формуласы бойынша
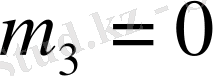 деп алып
деп алып
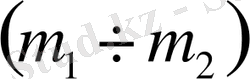 параметрлік жазықтығы үшін
параметрлік жазықтығы үшін
 -
матрицасының сипаттамалық полиномының коэффициенттерін табайық.
-
матрицасының сипаттамалық полиномының коэффициенттерін табайық.
n =3 болғандықтан, (1. 5. 8) теңдеулер жүйесі келесідей болады:
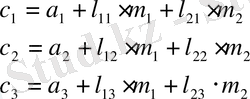 ,
,
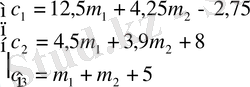
Осы алынған коэффициенттер арқылы объектінің сипаттамалық полиномын анықтайық.
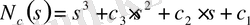


Енді
 енгізіп сипаттамалық полиномды нақты және жорамал бөліктерге бөліп аламыз.
енгізіп сипаттамалық полиномды нақты және жорамал бөліктерге бөліп аламыз.

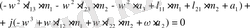

Жақшаларды ашып (1. 5. 11), (1. 5. 12) формулалары бойынша құрауыштарға бөлеміз.
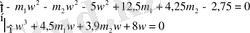
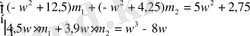
(1. 513) -( 1. 5. 15) формулаларын қолданып анықтауыштарды анықтаймыз.
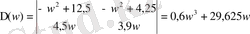
 графигі Қосымша А-да келтірілген (Сурет-2) .
графигі Қосымша А-да келтірілген (Сурет-2) .
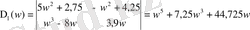
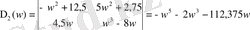
Табылған анықтауыштардан (1. 5. 16) формулаға сәйкес
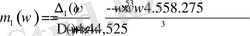
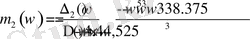
теңдеулерін құрастырамыз.
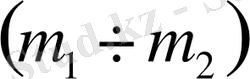 параметрлік жазықтықтағы шыққан графиктің дұрыстығын тексеру үшін (1. 5. 8) формуладағы
параметрлік жазықтықтағы шыққан графиктің дұрыстығын тексеру үшін (1. 5. 8) формуладағы
 деп алып түзу сызықтын графигін аламыз.
деп алып түзу сызықтын графигін аламыз.
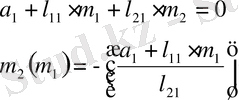
 -ға
-ға
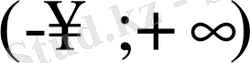 аралықтағы мәндерді беріп, D-бөліктеудің қисығын (
аралықтағы мәндерді беріп, D-бөліктеудің қисығын (
 ) параметрлер жазықтығында сызамыз.
) параметрлер жазықтығында сызамыз.
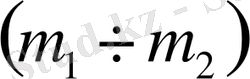 параметрлік жазықтығындағы графиктен Лапиталь ережесі бойынша
параметрлік жазықтығындағы графиктен Лапиталь ережесі бойынша
 нуктесін табу қажет, ол (1. 5. 17) теңдеуі бойынша табылады:
нуктесін табу қажет, ол (1. 5. 17) теңдеуі бойынша табылады:
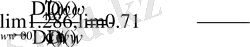
(1, 286; -0, 71) нүктесінде D-бөліктеу қисығы түзу сызығымен қиылысу керек. Бұл қиылысу нүктесі D-бөліктеу графигін жақындатып Қосымша А-да келтірілген (Сурет-1) .
Енді
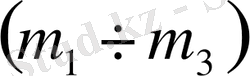 параметрлік жазықтығында D-бөліктеу әдісімен орнықтылық ауданын анықтайық. Алдымен (1. 5. 8) формуласы бойынша
параметрлік жазықтығында D-бөліктеу әдісімен орнықтылық ауданын анықтайық. Алдымен (1. 5. 8) формуласы бойынша
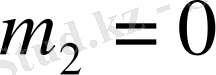 деп алып
деп алып
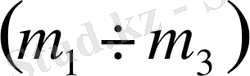 параметрлік жазықтығы үшін
параметрлік жазықтығы үшін
 -
матрицасының сипаттамалық полиномының коэффициенттерін табайық. Олар келесідей болады:
-
матрицасының сипаттамалық полиномының коэффициенттерін табайық. Олар келесідей болады:
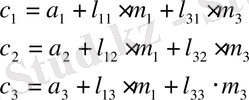 ,
,

Осы алынған коэффициенттер арқылы объектінің сипаттамалық полиномын анықтайық:
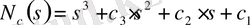

Енді
 енгізіп сипаттамалық полиномды нақты және жорамал бөліктерге бөліп аламыз.
енгізіп сипаттамалық полиномды нақты және жорамал бөліктерге бөліп аламыз.

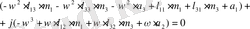
Жақшаларды ашып (1. 5. 11), (1. 5. 12) формулалары бойынша құрауыштарға бөлеміз.

(1. 5. 13) - (1. 5. 15) формулаларын қолданып анықтауыштарды анықтаймыз.
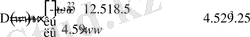
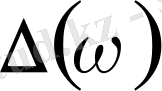 графигі Қосымша А-да келтірілген (Сурет-4) .
графигі Қосымша А-да келтірілген (Сурет-4) .


Табылған анықтауыштардан (1. 5. 16) формулаға сәйкес
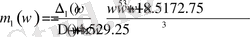
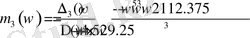
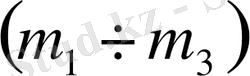 параметрлік жазықтықтағы шыққан графиктің дұрыстығын тексеру үшін (1. 5. 8) формуладағы
параметрлік жазықтықтағы шыққан графиктің дұрыстығын тексеру үшін (1. 5. 8) формуладағы
 деп алып түзу сызықтың графигін аламыз.
деп алып түзу сызықтың графигін аламыз.
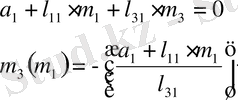
 -ға
-ға
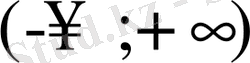 аралықтағы мәндерді беріп, D-бөліктеудің қисығын (
аралықтағы мәндерді беріп, D-бөліктеудің қисығын (
 ) параметрлер жазықтығында сызамыз.
) параметрлер жазықтығында сызамыз.
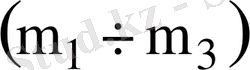 параметрлік жазықтығындағы графиктен Лапиталь ережесі бойынша
параметрлік жазықтығындағы графиктен Лапиталь ережесі бойынша
 нүктесін табу қажет, ол (1. 5. 17) теңдеуі бойынша табылады:
нүктесін табу қажет, ол (1. 5. 17) теңдеуі бойынша табылады:
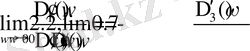
(2, 2; -0, 7) нүктесінде D-бөліктеу қисығы түзу сызығымен қиылысу керек. Бұл қиылысу нүктесі D-бөліктеу графигін жақындатып қосымша А-да келтірілген (Сурет-3) .
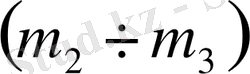 параметрлік жазықтығында D-бөліктеу әдісімен орнықтылық ауданын анықтайық. Алдымен (1. 5. 8) формуласы бойынша
параметрлік жазықтығында D-бөліктеу әдісімен орнықтылық ауданын анықтайық. Алдымен (1. 5. 8) формуласы бойынша
 деп алып
деп алып
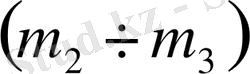 параметрлік жазықтығы үшін
параметрлік жазықтығы үшін
 -
матрицасының сипаттамалық полиномының коэффициенттерін табайық. Олар келесідей болады:
-
матрицасының сипаттамалық полиномының коэффициенттерін табайық. Олар келесідей болады:
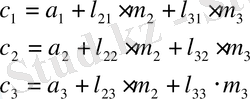 ,
,

Осы алынған коэффициенттер арқылы объектінің сипаттамалық полиномын анықтайық.
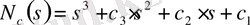

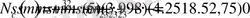
Енді
 енгізіп сипаттамалық полиномды нақты және жорамал бөліктерге бөліп аламыз.
енгізіп сипаттамалық полиномды нақты және жорамал бөліктерге бөліп аламыз.

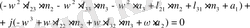
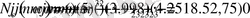 Жақшаларды ашып (1. 5. 11), (1. 5. 12) формулалары бойынша құрауыштарға бөлеміз.
Жақшаларды ашып (1. 5. 11), (1. 5. 12) формулалары бойынша құрауыштарға бөлеміз.
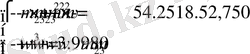

(1. 5. 13) -( 1. 5. 15) формулаларын қолданып анықтауыштарды анықтаймыз.
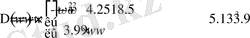
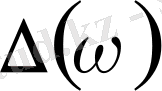 графигі Қосымша А-да келтірілген (Сурет-6) .
графигі Қосымша А-да келтірілген (Сурет-6) .


Табылған анықтауыштардан (1. 5. 16) формулаға сәйкес
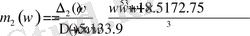
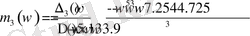
 параметрлік жазықтықтағы шыққан графиктің дұрыстығын тексеру үшін (1. 5. 8) формуладағы
параметрлік жазықтықтағы шыққан графиктің дұрыстығын тексеру үшін (1. 5. 8) формуладағы
 деп алып түзу сызықтын графигін аламыз.
деп алып түзу сызықтын графигін аламыз.
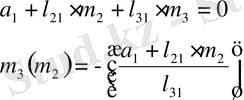
 -ға
-ға
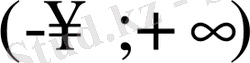 аралықтағы мәндерді беріп, D-бөліктеудің қисығын (
аралықтағы мәндерді беріп, D-бөліктеудің қисығын (
 ) параметрлер жазықтығында сызамыз.
) параметрлер жазықтығында сызамыз.
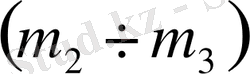 параметрлік жазықтығындағы графиктен Лапиталь ережесі бойынша
параметрлік жазықтығындағы графиктен Лапиталь ережесі бойынша
 нуктесін табу қажет, ол (1. 5. 17) теңдеуі бойынша табылады:
нуктесін табу қажет, ол (1. 5. 17) теңдеуі бойынша табылады:
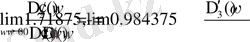
(-1, 71875; 0, 984375) нүктесінде D-бөліктеу қисығы түзу сызығымен қиылысу керек. Бұл қиылысу нүктесі D-бөліктеу графигін жақындатып қосымша А-да келтірілген (Сурет-5) .
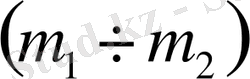 ,
,
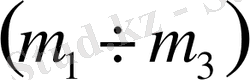 және
және
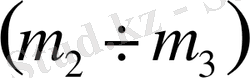 жазықтықтары үшін мәндері қосымша D - да көрсетілген.
жазықтықтары үшін мәндері қосымша D - да көрсетілген.
2. 5. 1 Раусс таблицалық сынымен техникалық жүйенің орнықтылығын анықтау.
Раусс кестесінің бірінші бағана элементтері ережеге сәйкес келмегендіктен, біздің техникалық жүйеміз асимтотикалық орнықсыз деген тұжырымға келеміз.
Енді келесі есептеулерді жүргізейік:
(1. 1. 1) - теңдікке сәйкес алатынымыз:
Орнықтылыққа тексеру үшін біздің 1-суреттегі (
 ) жазықтығының бөлінген түрінен координатты таңдап, (1. 1. 2) - теңдікке сәйкес Раусс матрицасын құрамыз. D
1
(3; -6) координатын таңдайық.
) жазықтығының бөлінген түрінен координатты таңдап, (1. 1. 2) - теңдікке сәйкес Раусс матрицасын құрамыз. D
1
(3; -6) координатын таңдайық.
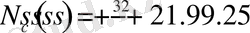
Кесте 2. 5. 1
(1. 1. 3) - теңдікке сәйкес матрицаның
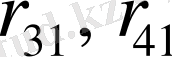 және
және
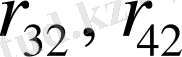 мәндерін тауып аламыз:
мәндерін тауып аламыз:
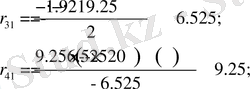
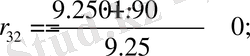
D 1 (2; 1) - орнықты аудан (2 нақты бөлігі оң түбір, 1 нақты бөлігі теріс түбір) .
D 2 (3; -2) координаты үшін:
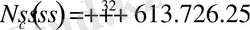
Кесте 2. 5. 2
(1. 1. 3) - теңдікке сәйкес матрицаның
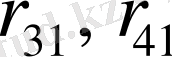 және
және
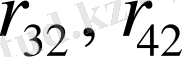 мәндерін тауып аламыз:
мәндерін тауып аламыз:
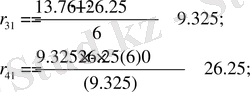
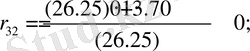
D 2 (0; 3) - орнықсыз аудан (0 нақты бөлігі оң түбір, 3 нақты бөлігі теріс түбір) .
D 3 (1; -4) координаты үшін:
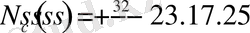
Кесте 2. 5. 3
(1. 1. 3) - теңдікке сәйкес матрицаның
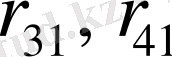 және
және
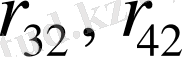 мәндерін тауып аламыз:
мәндерін тауып аламыз:
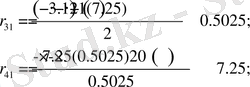
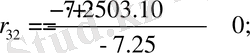
D 3 (1; 2) - орнықсыз аудан (1 нақты бөлігі оң түбір, 2 нақты бөлігі теріс түбір) .
Енді (
 ) жазықтығын тексерейік. (1. 1. 1) - теңдікке сәйкес алатынымыз:
) жазықтығын тексерейік. (1. 1. 1) - теңдікке сәйкес алатынымыз:
Орнықтылыққа тексеру үшін біздің 3-суреттегі (
 ) жазықтығының бөлінген түрінен координатты таңдап, (1. 1. 2) - теңдікке сәйкес Раусс матрицасын құрамыз. D
1
(5; 1) координаты үшін:
) жазықтығының бөлінген түрінен координатты таңдап, (1. 1. 2) - теңдікке сәйкес Раусс матрицасын құрамыз. D
1
(5; 1) координаты үшін:
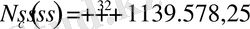
... жалғасыКесте 2. 5. 4
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz