Паскаль тіліндегі программалау

Жоспар

МАЗМҰНЫ
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3

I. ЕСЕПТЕУГЕ АРНАЛҒАН ТУРБО ПАСКАЛЬ ... ... ... ... ... ... ... ... ... . 5
1.1.Сандар теориясымен байланысты есептеулер ... ... ... ... ... ... ... ... 5
1.2.Жай сандар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 6
1.3.Полиномдармен есептеулер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 7
1.4.Сызықтық алгебра ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 11
1.5.Симметриялық матрицалар және меншікті мәндердің мәселесі... 13
1.6.Сызықтық емес теңдеулер жүйесін шешу ... ... ... ... ... ... ... ... ... ... 15
1.7.Интегралды есептеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 17

ІІ. ПАСКАЛЬ ТІЛІНДЕГІ ПРОГРАММАЛАУ ... ... ... ... ... ... ... ... ... ... . 19
2.1. Программа құрылымы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 19
2.2. Айнымалылар бөлімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 20
2.3. Операторлар бөлімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 21
2.4. Енгізу операторы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 23
2.5. Шығару операторы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 24
2.6. Меншіктеу операторы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 25
2.7. Параметрлік қайталау операторы ... ... ... ... ... ... ... ... ... ... ... ... ... 25

ІІІ. ГАУСС ӘДІСІМЕН ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУ ... ... ... ... ... ... 27

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 35
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 36
ҚОСЫМША ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 37

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 35 бет
Таңдаулыға:

КІРІСПЕ

Компьютер белгілі бір есептерді шешу үшін адам тарапынан сол есепті
қандай жолмен және қалай шығару керектігі туралы тапсырма алуы қажет. Бұл
тапсырмалар бір жағынан компьютерге түсінікті болып жазылуы керек болса,
екінші жағынан тапсырма беруші кісіге де ыңғайлы болғаны жөн. Осындай
компьютерлік тілде жазылған тапсырмалар мен командалар жинағы бағдарлама
деп аталады. Ал бағдарламалық мәтіндерді жазу үшін пайдаланылатын
символдардың жиынтығы компьютерлік тіл алфавитін құрайды.
Кез келген бағдарламалық тіл символдардан, сөздерден, сөз тізбектері
және сөйлемдерден (операторлардан) тұрады. Сөздер символдардан құралады, ал
операторлар сөз тіркестерінен тұрады. Қазіргі кезде бағдарлама жазу үшін
көптеген бағдарламалау тілдері қолданылады. Солардың бірі - Turbo Pascal
тілі құрылымының қарапайымдылығы мен игеруге жеңілдігінің арқасында
бағдарламалаушылардың арасында кеңінен қолданылады.
Енді бірер ауыз сөз тілдің тарихына тоқталатын болсақ, алгоритімдік
тіл АЛГОЛ 1950-1960 жылдары өңделді. Паскаль АЛГОЛ-дың ұрпағы болып
саналады. Оны өңдеген швециялық, жоғары техникалық училищесінің профессоры
Никлаус Вирт болды. Ол бұл тілді дүние жүзінде алғаш есептеу машинасын
жасаған ұлы француз ғалымы Блез Паскальдың құрметіне Паскаль деп атаған.
Паскальдың туған уақыты 70 жылдардың басы болатын.
Паскаль әмбебап программалау тілі - оқып үйренуге жеңіл, түрлі салалық
ақпаратпен жұмыс істеуге нәтижелі болғандықтан дүние жүзінде көп тараған
тілдердің бірі. Паскаль тілі:
– Алгоритм құрылымын сақтап құрылған;
– Жоғарғы деңгейлі программалау тілдерінің жақсы қасиеттерін жинақтаған;
– Қазіргі замандағы көптеген програмалау тілдерінің негізі болып табылады;
– ЭЕМ-нің мүмкіндігіне байланысты кеңейтіледі.
Бұл тілде жазылған программа компьтерде орындалу барысында алдымен
трансляцияланады машина тіліне аударылады, объектік программаға
түрлендіріледі де, содан кейін ғана орындалады. Осы сәтте компьтерде
программаның екі нұсқасы болады: біріншісі-алгоритмдік тілдегі алғашқы
түпнұсқасы, ал екіншісі-объектік кодтағы жазылған программа. Есеп нәтижесін
машиналық кодта жазылған программа арқылы аламыз, ал программаны түзету
қажет болғанда, оның алгоритмдік тілде жазылған алғашқы нұсқасы өңделеді.
Қазіргі кезде Паскаль тілі кез келген күрделі есептерді шығара
алатын, кең таралған стандартты оқу тіліне айналды.

I. ЕСЕПТЕУГЕ АРНАЛҒАН ТУРБО ПАСКАЛЬ
1.1. Сандар теориясымен байланысты есептеулер
Сандар теориясы есептеу тәжірибелеріне үлкен мүмкіндіктер ұсынады және
қызықты есептеу тапсырмаларының бай мәліметтер көзіне қызмет атқарады. Бұл
жерде біз жай ғана мысалды қарастырамыз.
Бірінші тапсырма мынадан тұрады-[m,n] интервалында жататын, 3-ке
немесе 7-ге қалдықсыз бөлінетін (бірақ бұл екі сан бірдей уақытта емес)
барлық бүтін сандарды қайта санау. Бұл үшін counting программасында
орындалған екі шешім ұсынылады.
Counting программасы. Counter 1 процедурасында минимальды бүтін мағына мен
максимальді бүтін мағына аралығындағы қарапайым таңдалым қолданылады. Әрбір
мағына үшін, егер бұл талап орындалса, есептегіш (счетчик) мағынасы 1-ге
артатын қатаң талап тексерісі жүргізіледі. Екінші жағдайда (сounter 2
функциясы) айқын математикалық формула қолданылады, сондықтан екінші шешім
оптимальды болып ұсынылады. Бұл осылай ма? Құрушыға мұны тексеру мүмкіндігі
ұсынылады, яғни екі функцияның орындалуына кететін уақыт шығынын өлшеу
арқылы (әрине, программалық жолмен). Бұл қарапайым мысалдағы назар
аударатын басты сабақ-есептеу тапсырмаларын шешу барысында алдын-ала ереже
сияқты математикалық зерттеу, оптимальды программалық шешімге келтіру.
Математиканы білмейтін программист сауатсыз жазушы сияқты.
Gcd программада үш түрлі әдіспен 0-ден басқа екі теріс емес санның ең
ортақ бөлгіші табылады. gcd 1 және gcd 2 функциясында рекурсия қолданылады,
бірақ екіншісі біріншісіне қарағанда тезірек жұмыс істейді. Бұл былай
түсіндіріледі, алгоритм модификациясы нәтижесінде функцияның рекурсивті
шақыруларының саны 55-тен 7-ге кішірейтіледі. gcd 3 функциясы итерационды,
бұл функцияның ішкі циклі 5-ақ рет орындалатынына қарамастан, ол одан да
доғары жылдам жұмыс істей алады. Берілетін математикалық тапсырма-осы үш
алгоритмнің де бірдей нәтиже беретіндігін дәлелдеу.
1.2. Жай сандар
р жай саны деп, 1-ден үлкен және 1 мен р-дан басқа бүтін бөлгіштері
жоқ сандарды айтамыз. max ең үлкен мәніне дейінгі аралықтағы барлық жай
сандарды табу үшін отсев алгоритмі қолданылады. Осындай белгілі
алгоритмдердің бірі Решот Эротосфен алгоритмі болып табылады. Бұл арада
отсев келесі түрдегідей өтеді. Бірінші сан, анықтамаға сәйкес екі. Барлық
қысқа сандарды бірінші жай санға, яғни 2-ге шегереміз. Ең кіші қалған үш
саны екінші жай сан болып табылады. т.с.с. Решот Эратосфен алгоритмі
eratosphen1 программасында орындалған.
Решот Эратосфен программасы.
Келесі программада жай сандарды іздеудің басқа алгоритмі көрсетілген,
яғни үлкен көлемдегі жай сандарды іздеуге арналған, сондықтан да оның
жадыдағы талабы пропорционалды 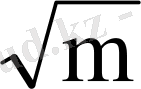, мұндағы m-жай сандар саны. Келесі
программа үшін бұл бағыныштылық m-ге пропорциональды болды. Программаның
орындалу уақыты 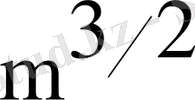-ге пропорциональ. Кіріс параметрінің мағынасы
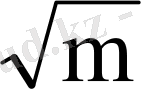(тұрақты п), ал жұмыстың нәтижесі- m-1 жай сан.
еratosphen2 программасының негізінде мына теориялар жатыр.
болсын. Бұл жай санның бірінен соң бірінің ілесу тәртібін
көрсетеді. Олай болса, әрбір n=2 үшін 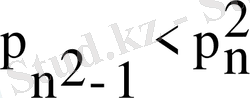теңсіздігі орындалады.
Сонымен, бірінші 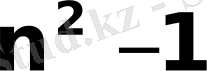жай санды табу үшін біз барлық санды 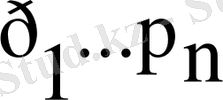қысқа жай
сандарға шегеруіміз керек. Осы жай санның кез келгені үшін р отсеиеваниесін
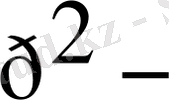тан бастауға болады. Сол сияқты кез келген аз қысқа сан қандай да бір
аз жай санға бөлінеді, демек істелінген жұмысты қайталаудың қажеті жоқ.
Алдын-ала өңделген жай санның әрқайсысы үшін сәйкес келетін барынша қысқа
сан көлемі жад талаптарын анықтайтын mult массивінде сақталады. Егер
жұмыстың нәтижесін сақтау үшін мысалы, файлға жазу қолданылса, онда prime
массиві қажет емес. Әрине, егер біз үлкен жай сандарды іздеуге кіріссек,
көптеген өзгертулерді wotd типінен longint типіне қайта анықтауға тура
келеді.
Решот Эратосфен программасы
еratosphen2 программасында өзгертілген р-қарапайымдылығына тексерілген
кезекті сан болып табылады, ал s жай санның квадратын сақтау үшін
қолданылады. mult[k] массиві қысқа prime[k] массивінің мағынасын 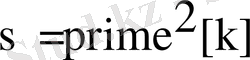-дан
бастап құрайды. Барлық табылған жай сандарды экранға сыйғызу үшін программа
әр жолында 50 жол мен 80 бағыты (позициясы) бар тексттік режимге қосылуды
іске асырады. Орындалған программа аяқталғаннан кейін режим бастапқы
қалпына келтіріледі.

1.3. Полиномдармен есептеулер
Бұл бөлімде біз келісілген есептеулер үшін классикалық ортогональды
полиномдардың берілген нүктедегі модулін қарастырамыз. Олардың рекурсивті
анықтамаларын еске сала кетейін. Чебышев полиномы келесі түрде анықталады:

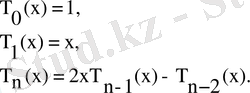
Лежандр полиномы:

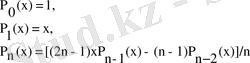
Эрмит полиномы:

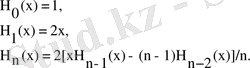
Және соңында Лагерр полиномы былай анықталады:

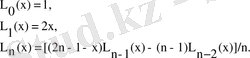
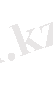
series модулінде деңгейлік қатармен кейбір математикалық опрациялар іске
асырылған. Еске саламын, деңгейлік қатар деп шексіздік түрін айтамыз.

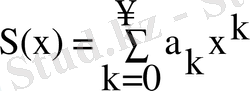
Мұндағы 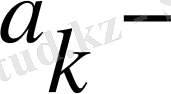сандық лщэффиценттер. Әрине, компьютер шектелген
операциялармен жұмыс істей алады, ал бұл полиномдар. Алдымен series
модулінде анықталған қатармен берілген операцияларды сипаттайық. Мына екі
қатар берілсін:

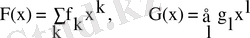
Қатар композициясы деп мына функция айтылады:
.
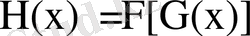Ғ(х) қатарының қатынасы деп у-ке қатысты х=Ғ(у) теңсіздігінің шешімін
айтамыз. n-ші деңгейлік қатары деп жаңа қатарды айтамыз
.
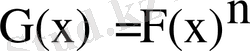Және соңында тағы бір операция-жеке екі қатарды анықтау:
H(x)=F(x)G(x).
Series модулінде полиномның максимальді деңгейі 20 деп болжанады, бұл
типтелмеген max_deg тұрақтының мағынасын құрайды. Қажет кезде бұл
тұрақтының мағынасын өзгертуге болады. Басқа eta тұрақтысы коэффиценттің 0-
ден кіші деп саналатын абсолютті ұзақ мағынасын анықтайды. Қатар (нақты,
полином, қысқартылған қатарға сай келуі) коэффицентінің мағынасы деңгей
үшін 0-ден максимальдік деңгейге дейін болатын заттай массив түрінде
сақталады.
Series модулінің интерфейсті секциясы:
unit series;
interface
const
max_deg=20;
eta=1.0e-20;
type
power_series=array[0..max_deg] of real;
var
Zero,One: power_series;
k:word;
procedure quotient (const F,G: power_series;var H: power_series);
procedure composition (const F,G: power_series;var H: power_series);
procedure invert (const F: power_series;var H: power_series);
procedure nth_power (const F: power_series; n:word; var G:
power_series);

Адын-ала саналған математикалық іс-әрекеттің қатармен анықталуын
қарастырайық. Жеке екі қысқартылған қатардың есептелуі келесі қатынасқа
негізделген. Егер H=FG, онда F=GH. Бұл қатынасты орнына қойып және бір
деңгейдегі х коэффиценттерін жинасақ, онда жеке Н коэффиценттеріне арналған
итерационды формула аламыз. Бұл алгоритм quotient процедурасында
анықталған.
сomposition процедурасы қатардың композициясын шектеуге арналған. Бұл
процедурада қолданылған алгоритм келесі қатынастарға негізделген:

.
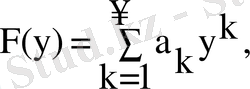
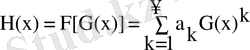invert процедурасында Феттис алгоритмі қолданылады. Біз Н(х)
деңгейлік қатарының Ғ(х) қатарына кері қатынасын іздейміз, сондықтан
,
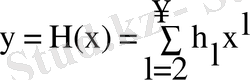соның ішінде
.
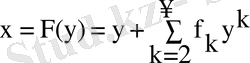Н(х) қатары 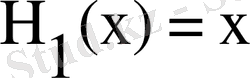-тан бастап, полиномдардың өсу деңгейі түрінде
құрылады. m қатарының 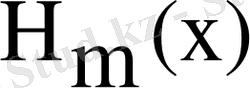полиномын табу қажет,
, (*)
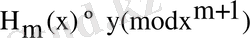яғни m=1 үшін орындалатын.
Егер 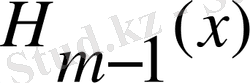қатары табылса, онда 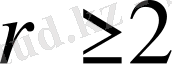үшін келесі қатынас орындалады:

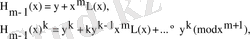
өйткені 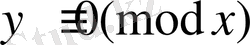. Мұндағы L(x)-бұл сондай шарт сақталатын х функциясы (*).
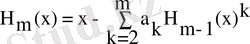болсын, онда
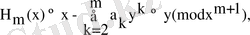дәлеледеу керегі де осы еді.
invert процедурасында полиномды бір бірлікке кіші деңгейлі по лином
бойынша есептеу үшін Горнер схемасы пайдаланылады:

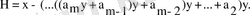
Р кейбір жай жақшаға дейінгі аралықта есептелген полином болып
табылсын. Онда келесі қадам басында Р:=Р-а есептеу қажет, ал содан соң
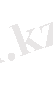
truncated_product ішкі процедурасы Р*Н туындысын есептейді. Ішкі
цикл for кері ретпен орындалады, сондықтан келесі қадамда қайта есептелген
Р коэффицентті қолданылмайды.
Тұрақты n-ші мүшесіз деңгейлік қатарын есептеу процедурасы-nth_power
келесі қатынастарға негізделген:

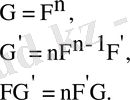
Соңғы теңсіздік бөлуден кейін ізденімді қатард коэффиценттері үшін
итерациондық сәйкестік береді.
Series инициализациясының модулінде нөлдік қатарға жауапты (zero)
массив форматталады.

1.4. Сызықтық алгебра
Сызықты алгебра матрицалардың қасиетін зерттеуге, сонымен бірге
сызықтық емес теңдеулер жүйесін шешуге арналған
Вх=с,
мұндағы В-жүйе матрицасының коэффиценті, с-оң бөліктің векторы, ал х-
компоненттері есептеуді қажет ететін белгісіздер векторы.
Біз айналысатын ең бірінші мәселе-сызықтық теңдеулерді алгебралық
жүйеде Гаусс әдісімен шешу. Бұл есептеу математиканың дәстүрлі тақырыбы.
Бұл сұраққа байланысты бай әдебиеттер қоры мен көптеген программмалар бар.
Осыларға енді бірнешеуін қосамыз. lin_alg модулі сызықтық теңдеулер жүйесін
шешуге арналған процедуралар жиынтығын құрайды. Кіріс мәліметтері деп, екі
блоктан тұратын, оның ішінде сол жақ блок В-жүйенің квадраттық матрицасы,
ал оң жақ блок С-сызықтық теңсіздіктің оң жақ бөлігіне қызмет ететін
біренше бағандардан тұратын А=[BC] матрицасын айтамыз. Сол себепті, жүйенің
шешімін бірден бірнеше оң жақ бөліктерімен қайта программалауға болады. С
блогы 1-ден бастап В блогындағы сандарға дейінгі аралықтағы кез келген
санды құрайды деп есептейміз.
Гаусстық алып тастау әдісі математикалық фактға ашылды, теңдеулер
жүйесінде коэффиценттер матрицасы шыққан матрицалардың жолдарын элементті
қосу бойынша алынды, кейбір жалпы көбейтілген көбейткіштер де дәл осылай
тұжырым жасай алады. Осы тәсілді қолдана отырып, төменірек орналасқан бас
диагоналдық матрицасының барлық элементтерін нөлге айналдыруға болады.
Үшбұрышты матрицалы теңдеулер жүйесі кері қоюмен оңай шешіледі. Ондай
уақытта ең бірінші үшбұрышты матрицалы жүйедегі соңғы теңдеу шешіледі, одан
кейін соңғының алдындағы және т.с.с. біріншіге дейін. Матрицаның басты
диагоналында нөлдік элементтің бар болуына байланысты сызықтық теңдеулер
жүйесін шешу кезінде қиындық туғызуы мүмкін. Мұндай жағдайда гаусстық
шығарып тастау үшін көбейткіштер таңдау мүмкін емес немесе Гаусстық жетекші
элементті таңдау әдісі қолданылады. Жетекші ретінде не бағандағы (жолдағы)
максимальды элемент, не барлық матрицадағы максимальды элемент таңдалады.
Осыдан кейін жолдарды (бағандарды) қайта қою жолымен бұл элемент матрицаның
басты диагоналына айналдырылады. Мұндай стратегия басты диагональдық нөлдік
элементінің болуына байланысты келеңсіздіктердің болмауына кепілдік береді
және әдісті тұрақты етеді. lin_alg модулінде жетекші жартылай таңдау әдісі
қолданылады. Егер бірінші фигуралы жақшадан кейін пробел алынып тасталса,
комментарий шартты компиляцияның дерективасына айналады, яғни ол
компиляцияланатын мәтінге жетекші элементтің толық таңдауының қолдануға
сәйкес келетін жаңа фрагменттерге енгізеді.
lin_alg модулінің интерфейсті секциясы.
unit lin_alg;
{$define complete_pivot}
interface
const
max_no_rows=20;
type
matrix=array[1..max_no_rows. 1..2*max_no_rows] of real;
Str10=string[10];
var
no_rows,no_cols:word;
singular:Boolean;
procedure get_system matrix (var A:matrix);
procedure get_rhs (var A:matrix);
procedure print_matrix (const A:matrix; name:str10;
screen_row,first_col, last_col:word);
procedure triangularize (var A:matrix);
procedure back_subtract (var A:matrix);

Алғашқыда матрица элементтері мағыналарын енгізу процедуралары
жүреді,оң бөлік векторлары және осы енгізудің дұрыстығын тексеру, яғни
элементтердің дұрыс енгізілмегендерін түзейтін мүмкіндіктер бар.
Әрі қарай жолдың осындай элементарлық пайда болуын жүзеге асырушы
процедуралар жүреді, яғни В жүйесінің матрицасын жоғарғы үшбұрышты түрге
келтіреді. Жетекші элементтің таңдау әдісі келесідей түрде жүзеге
асырылған. Бірінші р жолдарын өңдегеннен кейін (р+1)-дің соңына дейінгі
жолдарда табылатын р+1 бағанының ең үлкен (көлемі бойынша) элементі
анықталады. Сонан кейін (р+1)-ші жолымен табылған элементі бар жолдардың
орын ауыстыруы жүргізіледі. Осыдан кейін кейбір коэффицентке көбейтілген
жаңа (р+1) жол төмендегі барлық жолдардан олардың элементтерін нөлге
айналдыру үшін алынып тасталынады. Бұл әрекеттерді triangularize
процедурасы орындайды.
Жүйенің шешімі back_subtact процедурасымен табылады, яғни жолдардың
қосымша элементарлы пайда болуымен сол жақ блоктің бірлік матрицаға келуін
орындайды. Ол Гаусстың кері қою әдісін жүзеге асырады.

1.5. Симметриялық матрицалар және меншікті мәндердің мәселесі
Келесі тақырып-симметриялық матрицалардың меншікті мәндері мен
меншікті векторларын есептеу. А-n*n өлшемді заттық симметриялық матрица
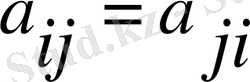
болсын. Симметриялық мтрица үшін 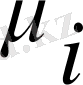меншікті мәндері және
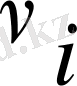меншікті векторлары үшін А матрицасы келесі жағдайларды орындайды:

Теорияға сәйкес, А симметриялық матрицаның барлық n меншікті мәндері
затты, ал оларға сәйкес меншікті векторлар ортономирлі базис түзеді.
Get_matrix және print_matrix процедуралары матрица элементтерінің
мәндерін енгізу және шығаруғы арналған. Көлемі бойынша үлкендеу меншікті
мәндерінің алгоритмін табу iterate процедурасына негізделген. Бұл
процедураны вектор-функциясы үшін итерационы орындайды:

Итерациялар е бірлік векторынан басталады және 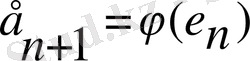векторларының
тізбегін береді. Басты векторды сәтсіз таңдаудың мүмкіндігі аз жағдайларды
ескермесек, онда итерациялар жүйесі жоғарғы меншікті мәнге сәйкес меншікті
векторға ұқсас болады. Бұл әдіс сатылы әдіс деген атпен белгілі.
QR_aigorithm процедурасында туынды заттық сингулярсыз симметриялық
матрицаның барлық меншікті мәндері мен векторларының іздеу алгортитмі
программаланған. Орындалуы 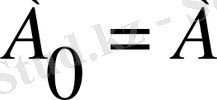меншіктеуден басталатын осы итерация
алгоритмінің қысқаша сипаттамасын келтірейік. Итерацияның n-ші жүрісі үшін
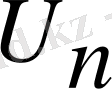матрицасы ортогональды, 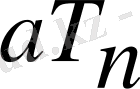оң диагональды элементі бар жоғарғы
үшбұрыш болып табылатын 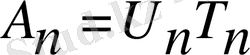матрицасының жалғыз көрінісі бар.
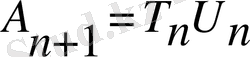салайық. Онда тізбек 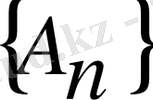диагональды матрица тәрізді болады,диагональды
элемент ролін А матрицасының меншікті мәндері атқарады. Егер барлық
меншікті мәндер жай және әр түрлі абсолюттік мәндерге ие болса, онда
ұқсастық кепілді. Теория бойынша 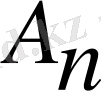және 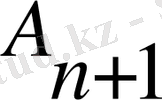матрицалары
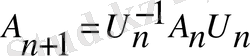қатынасымен байланысқа,бірдей меншікті мәндерге ие.
Көбейткіштердің туындылары түріндегі матрица көрінісі факторизация
деп аталады. Матрица факторизациясы-жалып жағдайда өте жай процедура. Егер
біз үш диагональды матрицамен жұмыс істесек, ол жылдам орындалады, басты
диагональ астыңғы диагональ, үстіңгі диагональдың болмауына байланысты
барлық элементтер нөлге тең. Егер A=UT матрицасы ең басынан үшдиагональды
болса,онда TU матрицасы да үшдиагональды, осылайша, 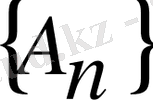жүйесінен барлық
матрицалар да үшдиагональды болады. QR-алгоритмінің реализациясы А
матрицасы эквивалентті үшдиагональды матрицамен алмасатын алдын-ала
жүрістен басталады. Бұл tridiagonalize процудурасы арқылы жүргізіледі. А
матрицасының TU-факторизациясы кейіннен тегіс қозғалыс жүйесімен
орындалады.
Алгоритм модификациясы оның жүруін жылдамдату мақсатында одан әрі
жүруі мүмкін. Егер саны 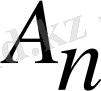матрицасының меншікті мәндерінің
аумағында мәндер қабылдаса,онда факторизация және итерация келесі түрде
жүреді:

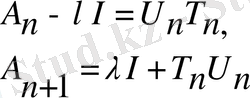
factor процедурасының белгіленуі m-шіден n-ші жолға джейінгі
диагональды блоктың факторизациясына негізделеді. Содан кейін muitiply
процедурасы есептеудің нәтижесін шығаруы тиіс.

1.6. Сызықтық емес теңдеулер жүйесін шешу
Сызықтық емес заттық теңдеулерді шешу үшін көбінесе, функция түбірін
жуықтап есептеу үшін Ньютон әдісі қолданылады, ол жанама әдісі деген атпен
белгілі. Бұл әдістің математикалық негізі мен сипаттамасын арнайы және
оқулық әдебиеттерден сандық әдістер бойынша табуға болады. Бұл алдымен
жуықтау,содан соң жүйелік дәлдік жүретін итерациялық әдіс. Ньютон әдісінің
қарапайым түбірге ұқсастығы басты жуықтауды таңдауға тәуелді. Мұнда біз
сызықтық емес теңдеулер жүйесін шешу үшін Ньютон әдісін қарастырамыз.
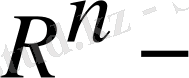n-ші өлшемді заттық вектор-бағандапрдың кеңістігі, ал D-осы
кеңістіктің облысы, F-тегіс функция болсын.
; .
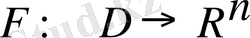Ньютондық итерацияларда бір ғана өзгеріс жағдайы үшін қолданылатын бірінші
реттің қарапайым туындысы якоб матрицасы -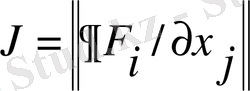. Берілген D-дағы х нүктесі
үшін Ньютон итерациясы келесі түрде болады:
,
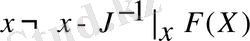мұндағы 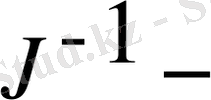якобқа кері матрица. Егер басты х жуықтау Ғ функциясының
түбіріне жақын таңдалса, онда жаңа х мәні дәл жуықтау болуы тиіс.
Қарастырып отырған алгоритмге негізделген программа барлық бірінші реттік
туындылардың есептеулерін реализациялауы тиіс. Тікелей әдісі-функцияның
аналитикалық есептелген туындыларын жай программалау. n=2 мысалын
қарастырайық

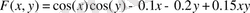
функциясының экстремумдарын оның бірінші туындыларының сараптамасы арқылы
есептейміз, тікелей айтқанда,екі бірдей бірінші жеке туындылардың жалпы
нөлдерін табамыз. Бұл есеп екі сызықтық емес теңдеулер жүйесін шешуге
әкеледі:

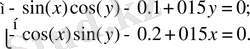
max тұрақтысы Ньютон әдісінің итерация итерация максимальды мәнін қояды,
бұл егер әдіс қандай да бір себеппен сәйкес келмей тұрса, онда итерациялық
процестің үзіліссіз қайталануынан қашуға мүмкіндік береді. eps тұрақтысы
жүйе шешімінің дәлдігін анықтайды, егер якобиан eta тұрақтысының аз мәнін
қабылдаса,жүйе сингулярлы деп аталады. Бұл жағдайда әдістің шығымы өте көп
болады және Ньютондық итерацияның әрі қарай жалғасуының маңызы болмайды.
F, G және dG функциялары экстремум ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.