Экономикалық-математикалық модельдеу классификациясы

Жоспар

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3

1. МАТЕМАТИКАЛЫҚ МОДЕЛЬ
1.1 Модель және модельдеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .6
1.2 Математикалық модельдер классификациясы ... ... ... ... ... ... ... ... ... ...9

2. ЭКОНОМИКАЛЫҚ.МАТЕМАТИКАЛЫҚ МОДЕЛЬ
2.1. Экономикалық.математикалық модельдеу түсінігі ... ... ... ... ... ... ... ..12
2.2. Математикалық модельдеу әдістерімен экономикалық салада қолдану ерекшеліктері ... ..14
2.3. Экономикалық.математикалық модельдеу классификациясы ... ... ... 16
2.4. Экономикалық.математикалық модельдеу сатылары ... ... ... ... ... ... ..20
2.5. Экономикалық.математикалық модельдеу әдістері ... ... ... ... ... ... ... .21

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...27
ПАЙДАЛАНЫЛҒАН ДЕРЕК КӨЗДЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ... ... ... ... ..29
ПРАКТИКАЛЫҚ БӨЛІМ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .30

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:

КІРІСПЕ

Қазіргі қоғамның мәдениеті, білімділігі, ой өрісі және ой жүйесі
дамыған кезеңде халық шаруашылығының кәсіпорындарының қандай түрі болмасын
оның экономикасын ұтымды басқаруда математикалық әдістерімен компьютерлерді
кеңінен қолдану қажеттігі әркімге белгілі. Математикалық экономикада және
басқа ғылымдарда кеңінен қолданылуы осы ілімнің өзіне тән ерекшелігі болып
табылады. Егер оның осы ерекшелігі түбегейлі экономикалық талдаумен
біріктіре отырып пайдаланылса, онда өндірістік жұмыстарды тиімді
ұйымдастыруында және басқаруда яғни әр істен ұтымды табыс табу жолдарында
математикалық әдістемелерді қолдану-бүгінгі таңдағы кең қажетті істің бірі.

Экономикалық – математикалық модель алынған мәлімет үнемі дайын
басқару шешімі бола бермейді, көбіне олар кеңес беруші қаржы саласында
пайдаланады,басқару шешімдерін адам қабылдайды. Бұл төтенше қиындықтар
экономикалық, әлеуметтік-экономикалық құбылыстар деп түсіндіріледі.
Экономикалық–математикалық модель осындай сәйкестік пен тек құраушысы болып
табылады, алайда негізгісі адам-машиналық жүйеде жоспарлаумен басқару халық
шаруашылығымен экономикалық бірлестіктердің деңгейі.
Экономикалық–математикалық модель процесінде көптеген кезеңдерден
өтеді нысанның идентификациясы, модельдің ерекшелігі, идентификация және
моделдің параметрлерінің бағасы. Бұл процесс, әдетте, бірнеше рет
қайталанады. Әр кезеңде модель анықталады,әсіресе тәжірибелік есепті шешуге
арналғанда соңғы жағдайда, алгоритмдеумен бағдарламалау технологиясы
жағынан қосымша талаптарды модельге ұсынады. Әр кезеңде құралған модельдер
белгілі бір тексеріс ережелерін қадағалай отырып жүзеге асырылады. Соның
өзінде жетіспеушіліктер байқалады,олар:
- модельге жоқ өзгерістерді қосу;
- модельге бір өзгерістердің қосылмай қалуы;
- моделге параметрлер бағасының нақты жетіспеушілігі;
- модельде құрылымының жетіспеушілігі, яғни анықтаманың дұрыссыздығынан
өзгерістер арасындағы тәуелділік, оңтайлылық қабылданған критерийінің
басқаруға тиімді және басқаруға тиімсіз өзгерістер деп бөлінеді.
Менің курстық жобамның тақырыбы Экономикалық-математикалық модельдеу
классификациясы. Бұл курстық жоба жалпы екі бөлімнен тұрады. Бірінші
бөлімде математикалық модель туралы қарастырылады. Бұл бөлімге модель және
модельдеу, математикалық модельдер классификациясы және экономикалық
есептердің математикалық моделін құру үлгілері тақырыптары кіреді.
Модель және модельдеу тақырыбында модель ұғымы, модельді
конструкциялау, модельдердің негізгі типтері, модельді көптеген әдістермен
классификациялау, абстрактылы модель, аналитикалық модель, имитационды
модель, структуралық модель, модельдеудің ережелері туралы қарастырылған.
Математикалық модельдер классификациясы тақырыбында математикалық
модель, математикалық модель классификациясы, математикалық модельді құру,
математикалық модельді құру сатылары туралы қарастырылады.
Экономикалық есептердің математикалық модельдерін құру үлгілері
тақырыбында өндірістік фабрикасына есеп қарастырылған. Бұл есепте сатудан
барынша жоғары табыс түсіретін карамель өндірудің жоспарын табу керек. Ал
ол үшін математикалық моделін құру, мақсат функциясын құру, есептің
шектелуін құру қарастылған. Екінші есебінде минималды құн шарты бойынша
малды азықтандырудың оңтайлы рационын анықтау керек. Мұнда математикалық
модельді құру үшін айнымалыларды енгізу, мақсатты функция құру туралы
қарастырылады.
Екінші бөлімде экономикалық-математикалық модельдеу түсінігі,
математикалық модельдеу әдістерімен экономикалық салада қолдану
ерекшеліктері, экономикалық-математикалық модельдеу классификациясы,
экономикалық-математикалық модельдеу сатылары, экономикалық-математикалық
модельдеу әдістері тақырыптары кіреді.
Экономикалық-математикалық модельдеу түсінігі тақырыбында
экономикалық-математикалық модель аналогиялық ұстанымына негізделетіні
туралы, экономикалық-математикалық модель модельдеу процесінде көптеген
кезеңдерден өтетіні, ең тиімді тәжірибелік модельдеу-ұқсас нысанды, дайын
модельді пайдалану процесі, сондай-ақ жеке блоктардағы
модельдерді–стандартты модельдер, өзіндік құндық модель принципі,
математикалық түйсік пен әдістер іздестірілуде модельдер жүйесі күрделі
жүйелер өзгерілген құрылымымен, динамикалық сипаттарымен айырбастау толық
емес, анықталмаған және толық құрамдалмаған анықтаманы қалыптастыратыны
туралы қарастырылады.
Математикалық модельдеу әдістерінің экономика саласында қолдану
ерекшеліктері тақырыбында экономикалық талдау мен есептеу әдістерін
жетілдіруде зерттеулердің математикалық тәсілдерін қолдану, экономикалық
бақылау әдістері, экономикалық процестердің сандық қатынастары туралы
қарастырылады.
Экономикалық-математикалық модельдеу классификациясы тақырыбында
экономикалық-математикалық модельдеудің әр түрлі классификациялары бары
туралы, көлемі жағынан экономикалық модельдер макромодельдер, локальдық
модельдер және микромодельдер болып бөлінетіні туралы, экономикалық
модельдер ішінде неғұрлым көп қолданылатындары корреляциялық талдау,
индикстік және сұрыптау методтары туралы, экономикалық-математикалық
модельдеудің жалпы классификациясы оннан астам негізгі белгілерден тұратыны
қарастырылады.
Экономикалық-математикалық модельдеу сатылары тақырыбында зерттеліп
отырған жүйе бейнеленуі оның жеке элементтерінің анықталуымен алға қойылған
мақсатпен олардың арасындағы байланысты гаморфты жүйесі туралы,
экономикалық-математикалық модель құрылғаннан кейін ерекшеліктері мен
таңдауларын анықтау мақсатында экономикалық-математикалық модельдердің
анализі жүргізілетіні, модельді қажетті қажеттіліктерімен қамтамасыз ету,
онымен жұмыс жасауда қауіпсіздікке кепілдік беріліп, жақсы нәтижелері
беретіні туралы қарастырылады.
Экономикалық-математикалық модельдеу әдістері тақырыбында
экономикалық есептерді шешу процесінде экономикалық жүйенің жеке
элементтері арасындағы тәуелділікті құру керектігі туралы, осы процесті
қолдануда математикалық аппарат сипаты бойынша классикалық және күрделі
математика әдістерін бөлу керектігі және де математика әдістерінің тобы
номенклатурасы бойынша әдістер түрлері, осы әдістердің түрлері тиімді
сызықтық программалау, математикалық статистикалар, комбинаторикалық
кестелер реті, ойындар, массалық қызмет көрсету, қорды басқару,
экспериментті бағалау туралы әдістерге тоқталып қарастырылады.
Курстық жұмыстың өзектілігі: Эконмикалық-математикалық модель құру
барысында модельдеу классификациясының мүмкіндіктерін ашып көрсету, сонымен
қатар артықшылықтарын ашып көрсету.
Зерттеу мақсаты: Экономикалық-математикалық модельдеудің
классификациясын анықтап, оның түрлерімен толық танысу.
Міндеті:
• Модель мен модельдеу түрлерін анықтау
• Модельдің түрлерімен танысу
• Есептің математикалық моделін құру
• Математикалық модель классификациясын зерттеу
• Экономикалық-математикалық модель классификациясын қамту.
Зерттеу объектісі: Ақтөбе гуманитарлық колледжінің компьютер класы.
Зерттеудің ғылыми болжамы: Мен бұл курстық жұмысымда есептеу және
модельдеу эксперименттерін жүзеге асырып, экономикалық есептердің
математикалық моделін құру әдістерімен толық таныстым.
Курстық жұмыстың зерттеу әдістері: Мен есептерді математикалық
модельдеу классификациясы әдісімен құрдым, модель құру үшін әр түрлі
амалдар мен әдістер қолдандым, құрған модельдің есептерде қолданылу
жолдарын анықтадым.
Зерттеу әдістері: Экономикалық-математикалық модельдеудің
классификацияларымен толық танысу.

1. МАТЕМАТИКАЛЫҚ МОДЕЛЬ

1. Модель және модельдеу

Модель мен модельдеу нақты мәселеден (есептен) оның шешіміне апаратын
негізгі ұстын (көпір).
Модель дегеніміз – нақты объектіні, процесті және құбылысты ықшам әрі
шағын түрде бейнелеп көрсету.
Модельдеу дегеніміз – объектілерді, процестерді немесе құбылыстарды
зерттеу мақсатында олардың моделін (макетін) құру.
Модель - ғылым танудың маңызды деген құралдарының бірі және зерттеу
объектісінің (немесе басқару) шартты бейнесі болып табылады. Модель
субъектпен конструкцияланады ( немесе басқарылады), себебі, объектінің
сипаттарын бейнелеу үшін (қасиеттер, байланыстар, структуралық және
функционалдық параметрлер және т.б), олар зерттеу мақсатында нақты
болады. Сондықтан да бұндай бейнелеудің сапасы – модельдің объектке
анықталған мақсатты соған қатыстырыларды тең шешу. Практикалық мәнді
модель келесі шарт орындалған жағдайда алады, ондағы әдістерге сәйкес
зерттеу субъектісіне анализі жақын, ол тікелей емес зерттеу объектісі
анализі одан төменірек.
Модельді конструкциялау келесілердің негізінде орындалады
объектінің қайта зерттелуі және оның нақты сипаттарын бөліп алу,
экспериментті және теориялық анализ моделі, объект туралы берілген
мәліметтер нәтижесінің берілуі, модель корректеровкасы және т.б бұлардың
барлығы модельдеу әдісінің негізгі құрамын құрады.
Модельдердің негізгі типтерін қарастырайық, модельдерді әр түрлі
сипаттарына қарай топтауға болады: модельдеуші объектілердің сипатына,
қосымшалар сферасы бойынша, модельдеу тереңдігі бойынша және т.б. Біз елді
модельдеудің сипаттық жағынан топтауға тоқталамыз (модельдеу әдістері
бойынша) себебі, экономикалық жүйелерді зерттеуде математикалық моделді
қолданылады.
Модельдерді көптеген әдістермен классификациялауға болады, алайда,
олардың біреуі де толығымен қанағаттанарлықтан емес. Неғұрлым толық және
түсінікті классификация моделіне Норенков модельдері жатады. Енді біз
сол модельмен танысамыз. Ең алдымен физикалық және абстрактылы модельдердің
айырмашылығын білу керек. Физикалық модель материалды құрылған жүйе,
мысал, макет, тренажёр, және экприментальды үлгі. Абстрактылы модель-
проектілеу объектісінің сипаты немесе кейбір тілде зерттеу жүргізу, мысалы,
график, сызба, схем, граф, кесте, формула, граф немесе блок- алгоритм
схемасы, ЭВМ үшін программа.
Абстрактылы модельдердің көп түрлілік моделіне математикалық модель
жатады. Мұндай моделде объектілерді сипаттау математикалық қатынастар
тілінде орындалады. Математикалық модельдер өз кезегінде аналитикалық және
имитационды болып екіге бөлінеді.
Аналитикалық моделдер теңдеу немесе теңдеулер жүйесінен тұрады. Олар
әріптік түрде жазылған және шешілген. Осыдан олардың аты алынған. Мысалы,
логикалық элементтің аналитикалық моделі 2И-НЕ келесі түрдей болады: А
және В белгілі мәндері арқылы F күйінің шығу мәнін анықтауға болады.
Модельде тек функцияларды ғана ескеріп қоймай, және басқа да шығу
параметрін беруге болады, мысалы, элемент арқылы сигналдардың
таратылуындағы кешігуін алуға болады. VHDL тілінде бұны жасау өте оңай:

F=not(A and B) after 20ns
Аfter 20ns сөзі F сигналы жаңа мән алатынын бірақ модельдеу уақытының
ағымдағы мәнінде еместігін білдіреді, бұл оператор орындаған жағдайда,
20ns уақыттан кейін, яғни F айнымалысы бұрыңғы мәнді біраз уақытқа дейін
сақтап тұрады.
Модельдерде тек үзілісті ғана емес, сонымен қатар элементтің жұмыс
жасауын да бейнелеуге болады. Мысалы, PML тілінде PCAD пакетінің
қарастырылып отырған элемент моделінің орындалуы. F шығуының соңғы
бөлігінде PCL- тізім келтірілген, мұнда үзілістер көрсетілген. Сонымен
қатар шығудың логикалық күші S болса ол лог.0 мәнін және логикалық
күші D болса ол лог.1 мәнін қайтарады.
PCAD пакетінде логикалық күштің төрт түрі бар: S,D,R және Z. Олар
мұнда кемуі ретінде орналасқан. S күшті шығу, ең күштісі болып табылады.
Имитационды модель оған сәйкес объект әрекетін немесе оның шығу
сигналдарын есептеу әдістерінің алгоритмдерінің (процедураларын) сипатынан
тұрады.
Дәл осы модель үшін, яғни 2И-НЕ элементі келесі түрдегі сөз болады:
егер А кіруі немесе В кіруі лог.0 тең болса, онда F шығуына лог.1
меншіктеу, әйтпесе лог.0.
Егер бұл шартты жазып, оны ішкі программа ретінде (процедура немесе
функция) алсақ, онда біз 2И-НЕ логикалық элементінің программалық
имитационды моделін аламыз. Қарапайым объектілер үшін аналитикалық модель
қарапайым және оңай болып табылады. Бірақ күрделі объектінің
аналитикалық моделін тұрғызып көріңіз, мысалы екілік есептегіш немесе
микопроцессор. Сіз математикалық теңдеулерді жалпы түрде шешу шарт
бойынша, орындалмайды, онда объектінің орындалу алгоритмін іздеу еш қиындық
туғызбайды. Сол себептен де имитационды модельдеуге ерекше көңіл бөлінеді.
Қарастырылған модельдерді жетектеуші немесе функционалды деп атайды.
Олардың ерекшелігі объектілерді сырттан сипаттайды да ішкі структурасы
ашылмайды, олар қара жәшік типті модель сияқты.
Біз объектінің функциясын білеміз, бірақ ерекше жағдайларда ғана
оның ішкі бөлігін біле аламыз. Жоғарда қарастырыған мысал да осы
айтығанды дәлелдейді. Модельге басқа да параметрлер қосуға болады.
Мысалы, орындалу үзілісін және жұмыс жасау қабілеттілігі логикалық
элемент модельдерінің кітапханасын құруға болады, содан кейін олардан
күрделі цифрлық объектілерді жинақтап (мысалы, түйіндер және
құрылғылар), бұл макеттеу процесіне өте ұқсас.
Біз модельдерді модельденуші құрылғы структурасына сәйкес
байланыстыруымыз керек. Мұндай модельдер структуралық деп аталады,
себебі олар объектінің ішкі құрылуын, структурасын сипаттайды.
Структуралық модельдер жетектеуші моделдерге қарағанда қызықты
болып саналады, себебі, базалық элементтердің аз ғана жиынтығы үшін, еш
қиындықсыз сандық түйіндер класын және құрылғыларды модельдеуге болады.
Сонымен қатар структуралық модельдерді тұрғызуда модельденуші
объектінің жүргізілуі туралы ақпаратты енгізу маңызды емес.
Күрделі объектіні декомпозициялау элемент дәрежесіне дейін немесе
компанент дәрежесіне дейін (транзистор, резистор және басқа да
радиодеталдар) орындалу структуралық примитивтер санының шексіз өсуіне
әкеледі.
Микропроцессор Pentium үш миллионнан астам транзистордан тұратынын
еске сақтайық.
Структуралық модельдеудің басқа да кемшілігі, қолданушы
микросхеманы сатып алып, әдетте олардың ішкі структурасын білмейді.
Мұндай ақпарат шарт бойынша шығарған фирманың құпиясы болып саналады және
қолданушыға берілмейді. Сондықтан да дайын ИМС кез келген дәрежедегі
жүктеуші модель ретінде сипаттау керек.
Алайда, ИМС-ті жетектеуші модел, ретінде сипаттау үшін функцияларды
ғана модель деп қана қоймай, микросхеманың уақытша параметрін де
модельдеу керек.
Объект функциясын беру арқылы сіз, бастапқы қадамды жасадыңыз, енді
модель логикалық құрылымды тексере алады. Бірақ проектіленуші құрылғылар
үлкен жиілік пен жылжамдықта жұмыс жасайды, мысалы, екілік есептегіш
моделін құрып, оның дұрсы есептеп тұрғанын көріңіз. Бірақ оның мәні 50
немесе 100 мГц жиілікте орындалады.
Модельде уақытша параметрлерді ескеру керек, мысалы, сигналды
таратылу үзілісі, тоқтау уақытты, кіру импульстарының минимальды ұзындығы
және тағы да басқа уақытша параметрлер.
Үзілістерді есепке алмайтын модельдеу функциональды немесе логикалық
деп аталады, ол үзілістерді ескеру арқылы модельдеу- логикалық уақыттық
деп аталады.
Модельдеудің ережелерінің бірінде: алдымен қарапайым базалық модель
тұрғызыңыз, содан кейін оны жолдандырыңыз, ол объектінің функциясын
дұрыс орындауы керек, содан кейін оған жаңа қасиеттер қосып, күткен мінді
алу керек.
Бұл мақсатқа жетудің негізгі жолы – қосымша структуралық модель
құру (регистрлік, трназисторлы дәрежеде болса да).
Келесі сұрақ туындауы мүмкін: жетектеуші модельді тұрғызудың керегі
не, егер оның структуралық түрі бар модельдеудің өнімділігін арттыру
үшін.
Себебі, жетектеуші модельдің жылдамдығы структуралық модельуге
қарағанда 10-100 есе, кейде мыңдаған есе үлкен болады.
Имитационды эксперименттер VMDL- модельдеу түрі оның әрекетінің кез-
келген деталін зерттеуге және дұрыс емес қолдануларды шығару немесе
микросхемалық дұрыс емес қосылуын болдырмайды.
Аналогты ИМС үшін осыған ұқсас стандарттар бар, олар SPICE –модельдері
деп аталады (аты PSpice модельдеу жүйесінен алынған).

1.2 Математикалық модельдер классификациясы

Математикалық модель классификациясы берілгендермен кең көлемде жұмыс
жасауда соның ішінде сұрыптау есептерінде көп қолданады.
Классификация объектілерді жүйелеуге мүмкіндік береді, оларды
зерттеуді жеңілдетеді, ойлау аймағын реттейді және маңызды ғылыми
сипаттарға әкеледі. Мысалы, химиялық элементтердің классификациясы
Менделеевті периодтық заңды ашуға әкелді.
Классификацияны жақтаушылар ешқашанда бұл мысалды ұмытпайды және бұны
классификацияның күшті аргументі ретінде санайды.
Экономикалық талдаумен есептеу әдістерін жетілдіруде зерттеудің
математикалық тәсілдерін қолдану үлкен роль атқарады. Баға белгілеу
заңдылықтары өнім бірлігіне жұмсалатын еңбек пен материалдардың толық
шығынын зерделеу салааралық байланыстарды зерттеу, капитал салымының
рентабельділігі, өндірісті орналастырудың тиімділігін анықтау өндірістік
процесті оңтайлы жоспарлау шектеулі ресурстарды тиімді пайдалану секілді
экономикалық проблемалар және басқа да маңыздылығы бұлардан кем емес
мәселелер математикалық тәсілдерді кеңінен қолдану табысты шешілі алады.
Экономикалық-математикалық зерттеу негізінде зерделеніп отырған
экономикалық процесті математикалық модельдеу, яғни бұл процестің сандық
заңдылықтарын математикалық формулалар көмегімен сипаттау жатыр.
Математикалық модельдердің көптеген анықтамалары бар. Солардың ішінде,
біздің пікірімізше, недәуір дұрыс болып табылатын біреуін берейік.
Математикалық модель – математикалық символдармен жазылған нақты құбылыс
абстракциясы. Оны талдау осы құбылыстың мәнін тереңдей ашуға мүмкіндік
беретіндей етіп құрастырылған.
Модельдеу дегенде біз модельдердің құрылуын, оларды зерделеу мен
қолдануды түсінеміз. Модельдеу процесінің мәнін сызба түрінде 1 – ші
суреттен көруге болады:

І саты

Модельдің құрылуы

ІІ саты
модельді зерделеу

ІІІ саты

Білімді модельден
нысанға аудару

1 – сурет
Модельді құрудың бірінші сатысында үш есепті шешу қажет:
- зерттеу мақсатын анықтау;
- негізгі шектеулерді айқындау;
- зерделеп отырған құбылыстың барлық мәліметтерінің сандық
көрінісі.
Зерттеу мақсаты есепті шешудің әр түрлі нұсқалары салыстырылатын және
олардың ішінен ең үздігі таңдалып алынатын белгісімен (критериімен)
сипатталады. Әр алуан экономикалық есептерде мұндай критерий ретінде
барынша жоғары табыс өндірістің барынша төмен шығындары және басқалар
таңдап алынуы мүмкін.
Әдетте, экономикалық есептер қою барынша тиімді пайдалануды қажет
ететін шектеулі ресурстардың бар екендігін білдіреді. Сондықтан зерделеніп
отырған мәселе үшін қандай ресурстардың шешуші болып табылатындығын,
олардың қоры қандай екендігін анықтау өте маңызды. Ресурстар бойынша барлық
шектеулер қарама-қайшы болмауы керек. Кейбір шектеулерді есепке алмау
алынған шешімнің қолдануға тиімсіз болып қалуына және керісінше ресурстар
бойынша қатаң шектеулер қою есептің шешімі аясын тым тарылтып жіберуге
әкелуі мүмкін. Бұл оңтайлы шешім табу мүмкіндігін жоққа шығарады.
Экономикалық есептерді шешудің барлығында математикалық тәсілдер
қолданыла бермейтінін атап өткен жөн. Бұл үшін қажетті шарт зерделеніп
отырған мәселені сиапттайтын есептер мен тәуелділіктердің бастапқы
деректерінің сандық көрінісі болып табылады.
Математикалық модельді құру сандық мәні есепті шешумен нұсқаларының
бірін анықтайтын айнымалылардың кейбір сандарын енгізуден басталады. Оларды
х, у және тағы басқаларымен белгілейді.
Оңтайлылықтың таңдалып алынған критериіне сәйкес мақсатты функция
құрылады. Содан соң математикалық теңдік немесе теңсіздік түрінде осы
процесті сипаттайтын өзара байланыстар бейнеленеді.
Жалпы түрде экономикалық есептің математикалық моделі мынадай түрге
ие:
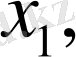
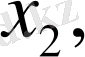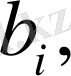( ..., ) і =

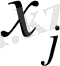
0,
Болған жағдайда функцияның экстримумын табу талап етіледі: .
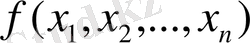Мұндай түрдегі экстремальды есептерді шешуге экономиказның әр алуан
есептерін талдау әкеледі.
Модельдеу процесінің екінші сатысында модель зерттеудің дербес
нысанасы ретінде көрінеді. Модельдік тәжірибелер жүргізіледі.
Үшінші сатыда модель тілінен түпнұсқа барабар еместігі айқындалуы
мүмкін. Бұл жағдайда модельді түзету, яғни бір сатыға өту жүргізіледі.
Осылайша, модельдеу – бұл циклдық процесс және ол зерттеліп
отырған нысананы жеткілікті дәрежеде нақты бейнелейтін модель құрылғанға
дейін жалғаса береді.
Анализ үшін модельдеу объектпен салыстырғанда, модельдеу, шарт
бойынша, объектінің қысқартылған бейнесіне әкеледі. Алайда, әрбір
орындалған зерттеуде алынған зерттеу нәтижелерін моделдеуіш объектке
ауыстырудың мүмкіндіктері, маңыздылығы неде екенін түсіну керек.
Демек, модельдер зерттеуде қарапайым болу жағынан таңдалады, мұнда
зерттеу объектісіне көп көңіл бөлінбейді. Кейде, кейбір объектілерді
зерттеу тіптен мүмкін емес, мысалы, мемлекет экономикасында, нақты мән
алатын эксперементтер жүргізу мүмкін емес. Дегенмен де, модельдеуде
ағымдағы объектінің кейбір маңызды деген жақтары ғана көрінеді,
модельдеу нақты факторларды көрсетуге мүмкіндік береді.
Сондықтан да, модельдеу екі үлкен топқа бөлінеді: материалдық
(заттық) және ерекше модельдеу. Материалды модельдеу әдістерін зерттеу
дегеніміз – зерттеу келесі зерттеулер негізінде жүргізіледі, геометриялық,
физикалық, динамикалық және функционалды сипаттары, мысалы, физикалық
моделдеу: самолет моделі алынады және аэро динамикалық трубада зерттеледі,
осыдан зерттелуші модельдердің сипаттары және бұл сипаттамалар ықтималдық
теориясы негізінен нақты аппаратқа түрлендіреді. Экономикалық зерттеулерде
нақты модельдеу қолданылады, олар модельденуші объектінің материалды
аналогиясына негізделген. Нақты модельдеуді екі ішкі класқа бөлуге болады:
белгі (сандық) модельдеу және интунтивті модельдеу.
Белгі модельдеуінде кейбір түрлердің белгілік құрылымы модель
ретінде аланады; олар модельдеу дәрежесінде өтеді. Мұндай модельдеу
ғылыми салаларда тану процесі бастапқы стадияда орналасқан кезде
қолданылады.
Идеалды модельдер негізінде жүргізілген зерттеулер теориялық
сипатта, олар эксперинеттерден, ерекшеленеді.
Идеалды моделдерді зерттеу – теориялық ойлау есебінің негізгі есебі болып
табылады. Идеальды модельдің орны экономикалық зерттеулерде маңызды
болады.

2. ЭКОНОМИКАЛЫҚ-МАТЕМАТИКАЛЫҚ МОДЕЛЬ
2.1 Экономикалық-математикалық модельдеу түсінігі

Экономикалық-математикалық модель дегеніміз – ақиқат экономикалық
процестерінің маңызды қасиетерін бейнелейтін математикалық жүйелер. Ол
экономикалық процестердің өзгешеіктерін және өзара байланыстарын белгілі
бір ережелер бойынша арнайы символдармен бейнелейді.
Барлық модельдеу тәрізді экономикалық – математикалық модель де
аналогия ұстанымына негізделеді, яғни нысанды зерттеу мүмкіндігі тікелей
емес, тек соған ұқсас қол жетерлік нысаны, оның моделін арқылы ғана
басқасын қарастыру. Бұл жағдайда қол жеткізер нысандарды бөліп,
экономикалық – математикалық модель модельді салу барысында немесе басқа
теориямен гипотеза құрумен квантификацияны шолушы болады, зерттелініп
жатқан мәселенің нақты түсіндірушісі бола алады.
Экономикалық-математикалық модельдерді құру кезеңдері:
1. Зерттеу объектісін бақылау
2. Экономикалық – математикалық есептердің мақсатын анықтап,
критериін таңдау
3. Алғашқы мәліметтерді жинау және өңдеу
4. Экономикалық-математикалық модельдерді құру
5. Модельді компьютерде шығару, табылған нәтижені талдау. Егер шешім
зерттеушіні
қанағаттандырмаса, онда төртінші кезеңге оралу қажет, яғни модельдерді
анықтау.
6. Анықталған модель бойынша есепті компьютерде қайта шығару
7. Табылған жаңа шешімді талдау және тәжірибе жүзінде қолдану.
Экономикалық-математикалық модельдерді құру принциптері:
1. Қажетті түрде модельдердің нақтылығын және толықтылығын қарау
үшін бірден зерттеушінің қасындағы негізгі деректердің дәліректілігі мен
екіден алынатын нәтижелерімен таразылау.
2. Математикалық модель зерттеліп отырған құбылысты онша
ықшамдамай, негізгі жақтарын айқын көрсету керек.
3. Шынайы құбылысқа математикалық модель толық және адекватты
болуы мүмкін емес, сондықтан құбылысты зерттеген кезде бірнеше модель
пайдаланған дұрыс. Егер оптикалық нәтмжесі бірдей болып шықса, онда ол
модельдердің бірімен шектеледі, ал егер нәтиже әртүрлі болса, онда есепті
қайтадан құру керек.
4. Кез – келген күрделі жүйе біраз ішкі және сыртқы әсерге ұшырайды.
Сондықтанда математикалық модель орнықты болуы қажет.
Экономикалық-математикалық модельдеудің негізгі 3 кезеңін көрсеткен
дұрыс болады:
1. Объектінің сапалық сипаттамасын жасап, зерттеудің мақсаты мен
міндеттері көрсетіледі.
2. Объектінің математикалық моделі құрылады. Модельді зерттеудің
методтары таңданып алынады немесе ондай методтар жаңадан жасалынады.
Модельдің есептеу машиналық модельге қажетті информациялары дайындалып,
одан соң машиналық модельдің жарамдылығы тексеріліп, оның нәтижесінің
дұрыстылығы анықталады.
3. Машиналық есептеу негізінде математикалық модель талқыланып
алынған нәтижелер өңдеуден өткізіледі. Сөйтіп, әрі қымбат, әрі көп уақыт
қажет ететін табиғи эксперимент экономикалық-математикалық модельдеу
процесімен ауыстырылады.
Оған қоса, қарастырылып отырған экономикалық есептің жоспарлары мен
басқарушылық шешімдерінің бірнеше варианттары өзара салыстырылады. Зерттеу
мақсатына сай оптималдық критерий тұрғысынан қарағанда ең жақсы жоспар мен
басқарушылық шешім таңдап алынады.
Мысалы авиаконструктордың өзі жобалаған ұшақтың жылдамдығының қандай
мәнінде күйрейтінін білгісі келеді. Ал эксперименттік машиналардың қымбат
тұратыны белгілі. Сондықтан ұшақтың ұшуы экономикалық-математикалық
модельдеуің көмегімен модельденіп, модель жылдамдығы шектік жылдамдыққа
дейін жеткізіледі. Ұшақтың математикалық моделі күйрейді, ал өзі аман
қалады. Бұл экспериментте ұшақтың көптеген агрегаттары мен бөліктерінің де
жұмысы жөнінде құнды деректер алынады. Тағы да бір артықшылығы:
математикалық модельдің бірнеше варианттарын сынап, солардың арасынан
тиімдісі таңдалынып алынады.
Электронды есептеуіш машинада математикалық модельдеу өнеркәсіпте
және саудада қолданылады. Мысалы, шикізат пен еңбек ресурстарын тиімді
пайдалану, дүкендер жүйесін тиімді орналастыру, жүк тасымалдарын тиімді
ұйымдастыру, тұтынушылардың сұрамын және оны қанағаттандыру деңгейін
болжау, дүкендерге сатушылар мен сатып алушылар арақатынасын тиімді
ұйымдастыру, базар жағдайының ертеңгісін болжап, ұйымдастыру мен
басқарушылық шешімдерін қабылдау т.б.
Модельдеу зерттеуде басқа зерттелінетін есептердің ашық құрылуын
гипотезамен тұжырымдаманың қатал логикасымен қалыптасуын қадағалайды.
Тәжірибелік есептер моделі болып біріншіден – талдаудың экономикалық
объектісі, екіншіден – экономикалық болжауда шаруашылық процесінің дамуын
көре білу, үшіншіден – басқарушының есебін қайта қадағалау бүкіл шаруашылық
иеархиясының теңдеуі.
Экономикалық – математикалық модель алынған мәлімет үшін үнемі дайын
басқару шешімі бола бермейді, көбіне олар кеңес беруші қаржы саласында
пайдаланады, басқару шешімдерін адам қабылдайды. Бұл төтенше қиындықтар
экономикалық, әлеуметтік-экономикалық құбылыстар деп түсіндіріледі.
Экономикалық–математикалық модель осындай сәйкестік пен тек құраушысы болып
табылады, алайда негізгісі – адам-машиналық жүйеде жоспарлаумен басқару
халық шаруашылығымен экономикалық бірлестіктердің деңгейі.
Экономикалық–математикалық модель модельдеу процесінде көптеген
кезеңдерден өтеді; нысанның идентификациясы, модельдің ерекшелігі,
идентификация және модельдің параметрлерінің бағасы. Бұл процесс, әдетте,
бірнеше рет қайталанады. әр кезеңде модель анықталады,әсіресе тәжірибелік
есепті шешуге арналғанда соңғы жағдайда, алгоритмдеумен бағдарламалау
технологиясы жағынан қосымша талаптарды модельге ұсынады. Әр кезеңде
құралған модельдер белгілі бір тексеріс ережелерін қадағалай отырып жүзеге
асырылады. Соның өзінде жетіспеушіліктер байқалады,олар:
• модельге жоқ өзгерістерді қосу;
• модельге бір өзгерістердің қосылмай қалуы;
• моделге параметрлер бағасының нақты жетіспеушілігі;
• моделде құрылымының жетіспеушілігі, яғни анықтаманың
дұрыссыздығынан өзгерістер арасындағы тәуелділік,оңтайлылық қабылданған
критерийінің басқаруға тиімді және басқаруға тиімсіз өзгерістер деп
бөлінеді.
Модельді қиындата отырып, оның ашық және толық мәлімет беруі үшін
есептеуінің қиындығына өтемақы алама, анығын білу қажет немесе оңай болуы
үшін сол элементтердің анықтығын біле отырып, оның шығынымен ұтысын
есептеп, біліп барып баға қояды.
Ең тиімді жол тәжірибелік модельдеу – ұқсас нысанды, дайын модельді
пайдалану процесі, сондай-ақ жеке блоктардағы модельдерді – стандартты
модельдер, өзіндік құндық модель принципін қалыстастырады.
Қазіргі уақытта жаңа математикалық түйсік пен әдістер іздестірілуде
модельдер жүйесі күрделі жүйелер өзгерілген құрылымымен динамикалық
сипаттарымен айырбастау толық емес, анықталмаған және толық құрамдалмаған
анықтаманы қалыптастырады. Осының бәрі математиканың жаңа бөлімі машиналы
имитация, математикалық –статистиканың модельдеу мәнінің артуына әкеледі.

2.2 Математикалық модельдеу әдістерінің экономика саласында
қолданылу ерекшеліктері

Экономикалық талдаумен есептеу әдістерін жетілдіруде зерттеудің
математикалық тәсілдерін қолдану үлкен роль атқарады. Баға белгілеу
заңдылықтары, өнім бірлігіне жұмсалатын еңбек пен материалдардың толық
шығынын зерделеу, салааралық байланыстарды зерттеу, капитал салымының
рентасльділігі, өндірісті орналастыруының тиімділігін анықтау, өндірістік
процесті оңтайлы жоспарлау, шектеулі ресурстарды тиімді пайдалану секілді
әкономикалық проблемалар және басқа да маңыздылығы булардан кем емес
мәселелер математикалық тәсілдерді кеңінен қолдану арқылы табысты шешіле
алады.
Мұндай есептер үшін құрамына желілік программалау, динамикалық
программалау, ойындар теориясы және басқа математикалық пәндер кешені
экономикалық нысандармен процестерінің математикалық модельдерімен бірге
кіретін экономикалық-математикалық аппарат әзірленді және одан әрі
жалғасуда. Бұл аппаратты, әсіресе өнеркәсіптік өндіріс, ауыл шаруашылығы
көлік, экономикалық зерттеулер және тағы басқа секілді салаларға қатысты
есептердің кең айналымын шешуге мүмкіндік беретін желілік программалауды
зерделеу экономистердің тәжірибелік жұмысында күннен-күнге қажеттілікке
айналуда.
Бұл көптеген экономикалық нысандармен процестерінің желілік модель
жеткілікті дәрежеде бар сипатталатындығымен түсіндіріледі.
Экономикалық ғылымда көптеген объектілер күрделі жүйе түсінігімен
сипатталуы мүмкін.
Жүйенің күрделілігі оған кірген элементтер санымен анықталады және
сонымен қатар орта мен жүйенің ара қатынасымен де анықталады. Мемлекет
экономикасы күрделі жүйелердің барлық белгілерінен тұрады. Олар үлкен
көлемді элементтерді біріктіреді және басқа жүйелерімен байланысуы
(табиғат ортасы, басқа мемлекет экономикасы және т.б).
Экономика күрделілігі кейде оның модельдеуінің мүмкін еместігін
көрсетеді, олар математика әдістерімен зерттеледі. Бірақ мұндай көз-қарас
принцип бойынша дұрыс емес. Кез-келген табиғаттағы және кез-келген
қиындықтағы объектілерді модельдеуге болады. Күрделі объектілер
модельдеуде қызығушылықты көп тудырады, дәл осында модельдеу нәтиже
береді, бұл нәтижені басқа модельдеу түрлерімен алуға болмайды.
Біріншілік ақпараттың дәлдігі және толықтығы нақты уақытта күрделі
моделдеудің типтерін таңдауды анықтайды. Ағымдағы ақпарат әр түрлі сипатта
болады және екі категорияға бөлінуі мүмкін: өткен уақыттағы және қазіргі
уақыттағы объектілердің күйі және болашақтағы уақытта объектілердің
дамуы;
Экономикалық бақылау әдістері және бұл бақылаулардың нәтижелерін
қолдану экономикалық статистикамен құрылады. Себебі, экономикада көптеген
процестер массалық болып табылады, яғни модельдеу массалық бақылауға
сүйеленуі керек. Экономикалық процестер олардың параметрлерінің
өзгешелігінен және структуралық қатынасына қарай динамикалық болып
саналады. Сондықтан да, мұндай экономикалық процестерді әр уақытта
бақылауда ұстау керек, міндетті түрде жаңа мәліметтер жиынтығын алып отыру
керек.
Экономикалық процестердің сандық қатынастарын тану және мұнда
құбылыстар экономикалық өлшемдерге сүйенеді. Өлшемнің дәлдігі мәндік
дәрежеде анықтайды және модельдеу арқылы табылған сандық анализдің соңғы
нәтижелерінің дәлдігі.
Экономикалық процестер массалық процестер сипатын сақтай отырып,
міндетті түрде кездейсоқ компенентерді қосуы керек. Ескертілмейтін
кездейсоқтықтар табиғаттық құбылыстардан болуы мүмкін, халықаралық
күйдегі өзгерістер, ғылыми – техникалық жаналықтар, әр түрлі субъектілік
факторлар осылайша, экономикалық заңдылықтар стохастикалық сипатта
болады.
Жоспарлау әдісі үшін маңызды мәнді экономикалық дамудың
белгісіздік мәні алады. Экономикалық талқылау бойынша зерттеулер мен
жоспарлау белгісіздіктің екі типін айырады: ақиқат, экономикалық
прцестер шартына негізделген және ақпараттық осы процестер туралы
толық емес және жеткіліксіз ақпараттар жиынтықынан тұрады.

2.3 Экономикалық-математикалық модельдеу классификациясы

Қазіргі таңда математикалық модель экономиканың әр түрлі
облыстарында талдау, болжау және оптималдық шешім құру үшін пайдаланылады.
Ол деген жоспарлау және өндірісті шұғыл түрде басқару, еңбек ресурстарын
басқару, қорды үлестіру және басқару, ресурстарды бөлу, объектілерді
жоспарлау және орналастыру, жобаны жетекшілеу, инвестицияларды бөлу және
тағы сол сияқты.
Модельдеу деп объектіні (процесті) тікелей зерттеу емес модельдер
деп аталатын көмекші объектілердің (процестердің) көмегімен талдап
зерттеуді айтады және экономикалық объектінің экономикалық математикалық
моделі деп, оның математикалық сипаттамасын айтады.
Бұл модель қарастырылып отырған экономикалық процестің (объектінің)
заңдылықтарын және қасиеттерін математикалық түрінде өрнектейді.
Экономикада модельдеуді пайдалану экономикалық объектінің құрылымын
айқындап, оның әртүрлі элементтері арасындағы маңызды байланыстарды
көрсетіп және объектіні басқарудың функциялық заңдылықтарын түсінуге
мүмкіншілік береді.
Экономикалық-математикалық модельдеудің әртүрлі классификациясы бар.
Бұл классификация қандай типологиялық негізде жүргізуіне, жекелеген
экономикалық ғылымдардың ерекшеліктеріне байланысты, функциялық белгілер
негізінде олар жоспарлау модельдері, бухгалтерлік есептер моделі,
статистикалық модельдер, экономикалық талдау модельдері, реттеу және
басқару модельдері т.б. бөлінеді. Бұл айтылғандарға қарағанда дербес
модельдерде бар. Мысалы, жоспарлау моделін болжау модельдері, техникалық –
экономикалық жоспарлау модельдері, оперативтік жоспарлау модельдері деп
бөлуге болады.
Саудада модельдерді көтерме және бөлшек сауда мен қоғамдық
тамақтандыру үшін жасауға болады. Сол сияқты жекелеген сауда орталығы,
аймақтағы және республикадағы сауда процесінің модельдерін құруға болады.
Көлем жағынан экономикалық модельдер, макромодельдер, локальдық
модельдер және микромодельдер болып бөлінеді.
Макромодельдер іріленген экономикалық көрсеткіштер негізінде бүкіл
халық шаруашылығын зерттеуде қолданылады. Бүкіл халық шаруашылығы күрделі
динамикалық жүйе ретінде қарастырылады.
Перспективалық жоспарлар жасалады, тиімді секторлық құрылымдық ара
байланысы анықталады:
а) микромодельдер бір, екі және көп секторлық болып бөлінеді.
Мысалы, екі секторлық модельге бүкіл халық шаруашылығы екі топқа-өндіріс
құралдар және тұтыну заттарының өндірісі болып бөлінеді. Неғұрлым толық
мәліметтерді, әрине, көп секторлық модельдер береді. Мұндай модельдерде
халық шаруашылығы ондаңан, тіпті жүздеген салаларға бөлініп, олардың бір-
бірімен ара байланысы қарастырылады. Макромодельдер жекелеген салалар
мысалы, сауда үшін де жасалады. Бұл жағдайда осы саланың глобалдық (жалпы)
мәселерді зерттеп, перспективалық жоспарлар жасалынады.
б) локальдық модельдерге шаруашылық салаларының әртүрлі
бағыттары (аспкетілері) талданып, соның негізінде болжамдар жасалады.
Мұндай модельдердің денін ғылыми-техникалық прогресті болжау, ұсыным мен
тұтынымды болжау, кадрлер қажеттігін болжау және т.б. құрайды.
с) өндірістік құрылымдарды терең талдау үшін микромодельдер
жасалады. Электронды есептеуіш машинасында осы модельдер негізінде
жүргізілген есептеулер өндірісті дұрыс ұйымдастыруға, пайдаланбай жатқан
ресурстарды, қорларды іске қосуға, соның арқасында дайын бұйымдар шығаруды
әжептәуір арттыруға мүмкіндік береді.Мысалы, оптималдық микромодельдер
автомобиль өндірісінде 25-50% дейін өнімді өсіруге қол жеткізеді.
Экономикалық микромодельдер ішінде неғұрлым көп қолданылатындары
корреляциялық талдау, индекстік және сұрыптау методтары. Бұлар саудада кең
қолданылады.
Мысалы, корреляциялық модельдер негізінде дүкендегі сатушылар саны
мен тауар айналымы арасындағы байланысты талдауға болады, т.б.
Пайдаланатын математикалық апаратқа байланысты экономикалық-математикалық
методтар: сызықтық жоспарлау модельдері, дөңес жоспарлау
модельдері,динамикалықстахаостықжос парлау модельдері, белгісіз жағдайларда
шешім қабылдау модельдері (ойындық модельдер), жаппай қызмет көрсету
модельдері, детерминдік модельдер болып бөлінеді және жоспарлау мен
басқарудың желілік модельдері делінеді.
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.