Жүк тасымалын тиімді модельдеу: математикалық модель және потенциалдар әдісімен шешу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 35 бет
Таңдаулыға:
МАЗМҰНЫ
КІРІСПЕ. . ……. . …3
НЕГІЗГІ БӨЛІМ
1. ЖҮК ТАСЫМАЛЫН ТИІМДЕУДІ МОДЕЛЬДЕУ
1. 1 Желілік программалаудың транспорттық тапсырмасының
берілуі және математикалық моделі . . . 5
1. 2 Транспорттық тапсырма моделінің ерекшеліктері . . . 7
1. 3 Бастапқы тірек жоспарды анықтау . . . 9
1. 4 Транспорттық тапсырманың тірек жоспарының
оңтайлылық өлшемі . . . …. . 14
2. ЖҮК ТАСЫМАЛДАУ ЕСЕБІН ПОТЕНЦИАЛДАР ӘДІСІМЕН ШЕШУ
2. 1 Алғашқы таяныш шешімді анықтау тәсілдері . . . 16
2. 2 Ең кіші элемент тәсілі . . . 18
2. 3 Тиімді шарттарын тексеру . . . 19
2. 4 Бір жоспардан екіншісіне ауысу. . 20
ПРАКТИКАЛЫҚ БӨЛІМ . . . 23
ҚОРЫТЫНДЫ . . . … . . . 33
ПАЙДАЛАНЫЛҒАН ДЕРЕК КӨЗДЕРІ ТІЗІМІ . . . 35
КІРІСПЕ
Экономикалық модельдеу ғылымы ертеректен зерттеліп келді және кейін бірте-бірте құрылыс және сәулет, астрономия, физика, химия, биология ғылымдарымен терең байланысты болды. Осы ғылымдардың барлығында экономикалық модельдеу іс жүзінде үлкен жетістіктерге жетті. Бірақ бұл жүйе ұзақ уақыт жеке ғылымдарда дамыды. Ұғымдардың бірыңғай жүйелері және терминдері болмады. Модельдеу ұғымы бірте-бірте ғылыми танудың әмбебап әдісі сияқты ұғындырыла бастады.
Модель термині әр түрлі адамдық қызмет сфераларында қолданылады және көпеген ұғымдардың жиынына ие.
Модельдеу - бұл басқару жүйелерін синтездеу және талдау үшін қолданылатын ғылымның ең басты ерекше әдісі. Бұл ерекше тәсіл ұқсастықты тану орнына зерттейтін объектінің субъектісін таңдайды немесе оған қосалқы объекті бейнесін немесе үлгісін жасайды, оны зерттейді және жаңадан алынған білімді түпнұсқаға жинақтайды.
Өзінің мүмкіндіктерін тиімді пайдалану арқылы жоғары нәтижеге жету кез келген адамның негізгі мақсаттарының бірі. Экономикалық жүйелердің әр түрлі деңгейлерінде кездесетін жоспарлау, басқару, шектелген ресурстарды тиімді бөлу, өндірістік процестерді талдау, күрделі объектілерді жобалау сияқты есептердің ұтымды және оптималды шешімдерін табу табиғи және ғылыми-техникалық прогресс қажеттіліктерінен туған мәселелер.
Оптимизациялық есептерде математикалық әдістерді пайдалану үшін, ең алдымен, тиімді шешімін табу қажет және есептің өзінің математикалық қойылымын жазуымыз қажет. Математикалық қойылымда берілген ресурстар, өндірістік технология, «жақсы» немесе «жаман» шешім деген сияқты түсініктердің сан шамалары және олардың арасындағы байланыстар, математикалық өректер, теңсіздіктер арқылы көрсетілулері тиіс. Шарттары нақты берілген есептің математика тіліндегі формалды жазылымын сол есептің математикалық моделі деп атайды.
Математикалық модель құру үшін, ең алдымен, зерттейтін объектінің ең басты қасиеттерін немесе заңдылықтарын бөліп алып, оларды математикалық өрнектер арқылы өзара байланыстырып сипаттайды. Математикалық модель құрғаннан кейін ғана есепті шешіп, зерттеу үшін математикалық әдістерді қолдануға болады.
Экономикалық процестердің математикалық модельдерін құрастыру өте күрделі мәселе, себебі ол үшін математикалық және экономикалық білгірлікті өзара ұштастыра білу қажет.
Оптимизациялау теориясында мүмкін болатын шешімдердің ішінен мақсат функциясы деп аталатын функцияға ең үлкен немесе ең кіші мән беретін «ең жақсы» шешімді табу әдістерін зерттеу мәселелері қарастырылады. Мысалы, кез келген өндіріс фирмасының негізгі мақсаты - көбірек пайда табу.
Осы экономикалық математикалық есептерді шешудің тиімді тәсілдерін пайдаланып, оларды зерттеуге байланысты мен курстық жұмысымның тақырыбын «Экономикалық өндірісте жүк тасымалының тиімділігін модельдеу» деп алдым. Бұл курстық жұмыс екі бөлімнен тұрады. Бірінші бөлімде транспорттық есептердің ішіндегі жүк тасымалын тиімдеу есептерінің моделін құруды, олардың тапсырмаларының берілуі қарастырылды. Есепті шешу барысында модельдің ерекшеліктері мен оңтайлы шешімдерін табуды жоспарлау жолдары бар. Екінші бөлімде есепті шешуде нақты жауап алу үшін түрлі экономикалық әдістерді пайдалануды жаздым.
Курстық жұмысымның өзектілігі: экономикалық процестердің математикалық модельдерін құрастыруда математикалық және экономикалық білгірлікті өзара ұштастыру. Транспорттық есептерді тиімді әдіспен шығарып, ең аз шығынмен ең көп пайдаға жетуді жоспарлау.
Курстық жұмысымның мақсаты: транспорттық есептерді шешуде өзінің мүмкіндіктерін тиімді пайдалану арқылы жоғары нәтижеге қол жеткізу.
Экономикалық процестердің әр түрлі деңгейлерінде кездесетін жоспарлау, басқару, шектелген ресурстарды тиімді бөлу, өндірістік процестерді талдау, күрделі объектілерді жобалау сияқты есептердің ұтымды және оптималды шешімдерін табу. Есепті түрлі тиімдеу әдістерін пайдалана отырып шығарып, олардан алынған нәтижелерді салыстырып, нақты және тиімді шешім алу.
Курстық жұмысымның мазмұны: Кіріспеден, екі тараудан, практикалық бөлімнен, қорытындыдан және дерек көздер тізімінен тұрады.
Зерттеу міндеттері:
- Жүк тасымалын тиімдеудің моделін құру;
- Математикалық моделін анықтау;
- Жүк тасымалының тиімділігін шешу әдістері;
Ғылыми болжамы: Жүйелік программалаудың жалпы тапсырмаларын шешудегі секілді, транспорттық тапсырманың оңтайлы жоспарын іздестіру және оның қандай да бір тірек жоспарын табу.
Зерттеу объектісі: Delphi программалау ортасы.
1. ЖҮК ТАСЫМАЛЫН ТИІМДЕУДІ МОДЕЛЬДЕУ
1. 1 Желілік программалаудың транспорттық тапсырмасының берілуі және математикалық моделі
Желілік программалаудың (ЖП) көптегеп тапсырмаларының ішінен арнайы тапсырмалардың кейбір топтары бөлініп көрсетілді. Оларды жалпы тәсілдермен шешу есептік сипаттағы бірқатар қиыншылықтармен бірге жүреді. Осыған байланысты арнайы, едәуір қарапайым шешу тәсілдері әзірленді. Тапсырмалардың осындай топтарының бірі транспорттық тапсырмалар болып табылады.
Тапсырманың берілуі. А1, А2, . . . , Аm-нің m жіберілу пункттерінде біртекті жүктің, сәйкес а1, а2, . . . , аm бірлігі бар, ол В1, В2, . . . , Вn-нің n тұтыну пункттеріне жеткізілуі керек (1 - кестеде көрсетілген) . Ал оларға сұраныс сәйкесінше в1, в2, . . . , вn бірлігін құрайды. Мұнда А пунктінен В пунктіне (і=
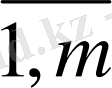 , j=
, j=
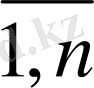 ) жүк бірлігін тасымалдауға жұмсалатын транспорттық шығындар С берілген. Барлық жүк жіберілу пунктінен толығымен шығарылатын, барлық тұтыну пункттеріндегі сұраныс қамтамасыз етілетін және транспорттық шығындар сомасы минималды болатын тасымалдау жоспарын анықтау керек.
) жүк бірлігін тасымалдауға жұмсалатын транспорттық шығындар С берілген. Барлық жүк жіберілу пунктінен толығымен шығарылатын, барлық тұтыну пункттеріндегі сұраныс қамтамасыз етілетін және транспорттық шығындар сомасы минималды болатын тасымалдау жоспарын анықтау керек.
b
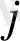
a
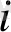
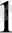
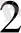
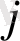
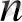
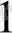
C
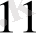
X
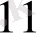
C
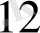
X
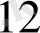
C

X
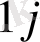
C
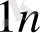
X
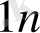
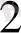
C
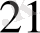
X
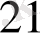
C

X

C
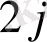
X
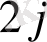
C
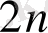
X
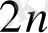
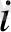
C
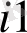
X
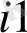
C
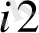
X
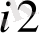
C

X

C
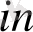
X
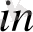
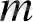
C
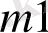
X
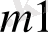
C
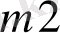
X
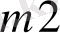
C
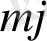
X
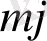
C

X

1 - кесте. Тапсырманың бастапқы мәліметтерін бөлуші
Тапсырманың математикалық моделі. Тапсырманъң математикалық моделін құру үшін А
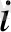 (і=
(і=
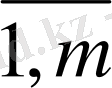 ) пунктінен В
) пунктінен В
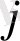 (j=
(j=
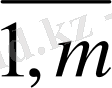 ) пунктіне тасымалданатын жүк бірлігінің көлемін білдіретін Х
) пунктіне тасымалданатын жүк бірлігінің көлемін білдіретін Х

 0 (і=
0 (і=
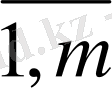 , j=
, j=
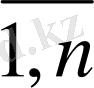 ) айнымалыларын енгіземіз. Бұл ауыспалылар келесі шарттарды қанағаттаңдыруы керек:
) айнымалыларын енгіземіз. Бұл ауыспалылар келесі шарттарды қанағаттаңдыруы керек:
а) барлық өнім жіберілу пунктінен шығарылуы керек:
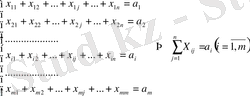
b) Барлық тұтыну пунктеріндегі сұраныс толығымен қанағаттандырылуы керек:
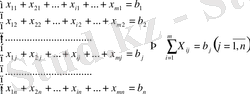
с) Тасымалдау тек бір бағытта, яғни
A
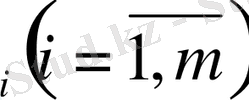 Equation. 3 пунктінен B
Equation. 3 пунктінен B
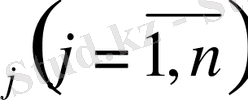 Equation. 3 пунктіне X
Equation. 3 пунктіне X
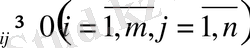 Equation. 3 жүреді.
Equation. 3 жүреді.
d) Транспорттық шығындар сомасы минималды болуы қажет:
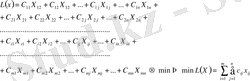 Equation. 3
Equation. 3
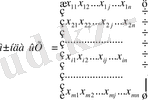 - тасымалдау жоспары
- тасымалдау жоспары
Осылайша, тансырманың математикалық моделі мынадай түрге ие болады:
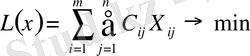 (1)
(1)
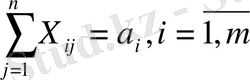 (2)
(2)
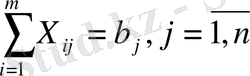 (3)
(3)
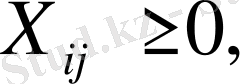
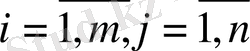 (4)
(4)
- Транспорттық тапсырма моделінің ерекшеліктері
Көріп тұрғанымыздай, (1) -(4) модельдері - Жүйелік программалау тапсырмасының моделі. Бірақ оның бірқатар ерекшеліктері бар. Бұл ерекшеліктер транспорттық тапсырманы шешудің едәуір ыңғайлы есепгеу тәсілдерін даярлауға мүмкіндік берді және бұл ерекшеліктердің мәні (2) -(3) шектеу жүйесінің салыстырмалы түрдегі қарапайымдығында:

А матрицасының барлық элементтері 1 және 0-ден тұрады және мұндағы әрбір бағанда тек екі бірлік (1) қана бодады.
Шектеу жүйесін векторлық түрде жазалық:

Осылайша, векторлық түрдегі транспорттық тапсырма моделі мынадай түрге ие болады:
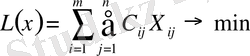 (1)
(1)
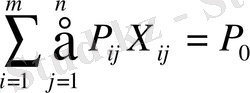 (5)
(5)
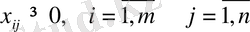 (4)
(4)
1-анықтама: Х=
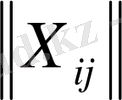 mxn матрицасымен анықталатын (2) -(4) жүйесінің теріс емес әрбір шешімі (1) -(4) транспорттық тапсырмасының жоспары деп аталады.
mxn матрицасымен анықталатын (2) -(4) жүйесінің теріс емес әрбір шешімі (1) -(4) транспорттық тапсырмасының жоспары деп аталады.
2-анықтама: Х=
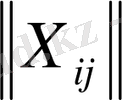 mxn жоспары егер нольдік емес коэффициентті (5) теңдікке кіретін
mxn жоспары егер нольдік емес коэффициентті (5) теңдікке кіретін
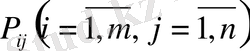 векторлар желілік тәуелсіз болса, тірек жоспары деп аталады.
векторлар желілік тәуелсіз болса, тірек жоспары деп аталады.
3-анықтама: (1) мақсатты функциясы минималды мәнге ие болатын X=
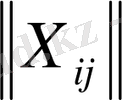 mxn жоспары оңтайлы жоспар деп аталады.
mxn жоспары оңтайлы жоспар деп аталады.
1-теорема. (1) -(4) тапсырмалары шешімді болу үшін
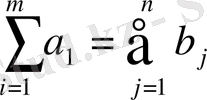 (6)
(6)
шартының орындалуы қажет және ол жеткілікті.
Мұнда транспторттық тапсырма моделі жабық деп аталады.
2-теорема. (2) -(3) шектеулер жүйесінің А матрицасының рангі шектеулер санынан 1-ге кіші, яғни r(A) =m+n-1.
Теоремадан желілік тәуелсіз
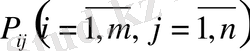 векторларының барынша жоғары саны тек (m+n-1) бола алатындығы, ізінше, транспорттық тапсырманың X=
векторларының барынша жоғары саны тек (m+n-1) бола алатындығы, ізінше, транспорттық тапсырманың X=
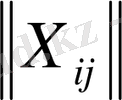 mxn тірек жоспарында (m+n-1) -ден аспайтын нөлдік емес компоненттердің бола алатындығы айқындалады. Кері жағдайда ол тудырылған деп аталады.
mxn тірек жоспарында (m+n-1) -ден аспайтын нөлдік емес компоненттердің бола алатындығы айқындалады. Кері жағдайда ол тудырылған деп аталады.
1. 3 Бастапқы тірек жоспарды анықтау
Жүйелік программалаудың жалпы тапсырмаларын шешудегі секілді, транспорттық тапсырманың оңтайлы жоспарын іздестіру де оның қандай да бір тірек жоспарын табудан басталады.
Транспорттық тапсырманың бастапқы тірек жоспарын анықтаудың бірнеше әдісі бар. Оның екеуін - батыс бұрыш әдісін және минималды элемент әдісін қарастыралық. Бұл тәсілдердің мәні мынада: тірек жоспары (m+n-1) қадамнан тысқары жатыр, оның үстіне әрбір кадамда жоспардың искомой матрицасының немесе жолы, иемесе бағаны анықталады.
Солтүстік-батыс бұрышы әдіс:
X=

жоспарын анықтау жоғарғы сол жақ бұрыштағы (солтүстік батыс) =Х
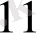 элементінен басталады.
элементінен басталады.
1-қадам.
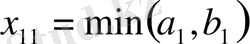
Екі жағдай болуы мүмкін:
А)
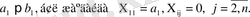
Осылайша, жіберудің А
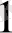 бірінші пункті барлық жүкті тұтынудың В
бірінші пункті барлық жүкті тұтынудың В
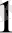 бірінші пунктіне бағыттады, яғни толығымен босады, сондықтан да басқа В
2
, В
3
, . . . В
бірінші пунктіне бағыттады, яғни толығымен босады, сондықтан да басқа В
2
, В
3
, . . . В
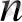 пункттеріне А
пункттеріне А
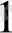 пунктінен ешқандай жүктің жіберілуі мүмкін емес. Матрица жоспардың алғашқы жолы осылайша анықталады, ал бөлуші кестеде бірінші жол жабылады. Мұнда алғашкы тұтынушының сұранысы
пунктінен ешқандай жүктің жіберілуі мүмкін емес. Матрица жоспардың алғашқы жолы осылайша анықталады, ал бөлуші кестеде бірінші жол жабылады. Мұнда алғашкы тұтынушының сұранысы
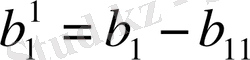 тең болады. Екінші қадамға көшейік.
тең болады. Екінші қадамға көшейік.
Б)
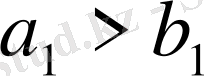 , бұл жағдайда
, бұл жағдайда
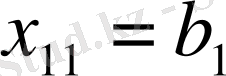 , ал бірінші бағанның қалған элементтері 0-ге тең, яғни
, ал бірінші бағанның қалған элементтері 0-ге тең, яғни
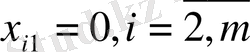 , себебі бірінші В тұтынушының сұранысы толығымен қанағаттандырылды, енді оған басқа
, себебі бірінші В тұтынушының сұранысы толығымен қанағаттандырылды, енді оған басқа
 жіберу пункттерінен жүк келмейді. Матрица-жоспардың, алғашқы бағаны осылайша анықталады. Мұнда бөлуші кестедегі бірінші баған жабылады, ал бірінші А
жіберу пункттерінен жүк келмейді. Матрица-жоспардың, алғашқы бағаны осылайша анықталады. Мұнда бөлуші кестедегі бірінші баған жабылады, ал бірінші А
 жабдықтаушы жүгінің көлемі
жабдықтаушы жүгінің көлемі
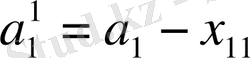 тең болады. Екінші қадамға көшейік.
тең болады. Екінші қадамға көшейік.
2-қадам. 1-қадамға сәйкес
А) жағдайында -
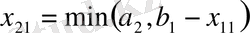 элементін, ал
элементін, ал
Б) жағдайында -
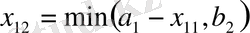 элементін анықтаймыз ж. т. б.
элементін анықтаймыз ж. т. б.
Бұл процесс жоспардың барлық элементтері аныкталғанға дейін жалғаса береді.
Теорема. Солтүстік-батыс бұрыш әдісінің нәтижесінде алынған жоспар тірек жоспар болып табылады.
Мысал:
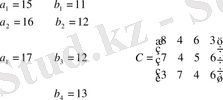
Солтүстік-батыс әдісімен бастапқы тірек жоспарды анықтаймыз
(2 - кесте) . Әуелі тапсырманың шешімділігін тексерейік:
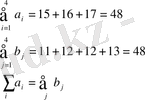
тапсырма шешімді.
Бөлуші кесте құрайық:
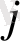 a
a
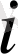
0
11
0
8
12
0
4
12
0
13
2 - кесте. Солтүстік-батыс әдісімен бөлу
1-қадам.
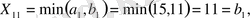 бұл жағдайда бірінші тұтынушы толығымен қанағаттандырылды, сондықтан
бұл жағдайда бірінші тұтынушы толығымен қанағаттандырылды, сондықтан
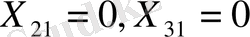 , ал бөлуші кестеде бірінші баған жабылады, мұнда жіберудің бірінші пунктінде
, ал бөлуші кестеде бірінші баған жабылады, мұнда жіберудің бірінші пунктінде
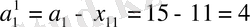 көлемде жүк қалады.
көлемде жүк қалады.
2-қадам. Бірінші бағанды анықтағаннан кейін матрица-жоспарда қалған жоғарғы сол жақ (солтүстік-батыс) элементті тағы да анықтаймыз:
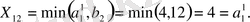 Бұл жағдайда бірінші А
Бұл жағдайда бірінші А
 жабдықтаушы толығымен босады, сондықтан В
жабдықтаушы толығымен босады, сондықтан В
 және В
4
пункттеріне одан ештеңе түспейді, яғни
және В
4
пункттеріне одан ештеңе түспейді, яғни
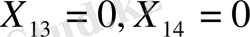 және бөлуші кестенің бірінші жолы жабылады, ал екінші тұтынушының сұранысы
және бөлуші кестенің бірінші жолы жабылады, ал екінші тұтынушының сұранысы
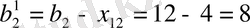 тең болады.
тең болады.
3-қадам. Сызылғаннан кейін қалған матрица-жоспарда жағарғы сол жақ (солтүстік-батыс) элементті тағы да анықтаймыз:
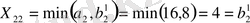
Көріп тұрғанымыздай, екінші тұтьшушының сұранысы толығымен қанағаттандырылды, сондықтан да үшінші жабдықтаушыдан оған ештеңе жіберудің керегі жоқ, яғни
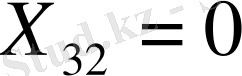 , бөлуші кестенің екініші бағаны жабылады, ал екінші жабдықтаушыда а
2
1
= а
2
-Х
22
= 16-8=8 көлемінде жүк қалады.
, бөлуші кестенің екініші бағаны жабылады, ал екінші жабдықтаушыда а
2
1
= а
2
-Х
22
= 16-8=8 көлемінде жүк қалады.
4-қадам. Екінші бағаны аныкталғаннан кейін қалған матрица-жоспарда элементті анықтаймыз:
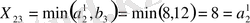
Екінші жабдықтаушы толығымен босады, сондықтан да тұтынудың, 4-ші пунктіне бұл жабдыктаушыдан жүк келмейді, яғни
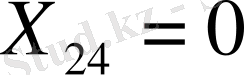 , сөйтіп бөлуші кестенің екінші жолы жабылады, сұраныс
, сөйтіп бөлуші кестенің екінші жолы жабылады, сұраныс
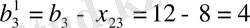 .
.
5-кадам. Х-ті анықтаймыз:
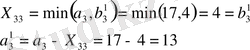
6-қадам. Жоспардың соңғы элементін анықтаймыз:
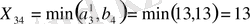
Осылайша, m+n-1=3+4-1=6 қадам арқылы бастапқы тірек жоспар анықталды:

Алынған жоспарға сәйкес келетін транспорттық шығындарды анықтаймыз. Оларды бөлуші кесте бойынша оңай есептеп шығаруға болады:
L(Х) =11*8+4*4+8*4+8*5+4*4+13*6=88+16+32+40+16+78=270
Солтүстік-батыс бұрыi әдісімен құрылған тірек жоспарда транспорттық шығындар көрсетілмейді, сондықтан алынуы мүмкін шешім оңтайлы шешімнен алшақ болады. Оңтайлы шешімге минималды элемент тәсілімен анықталған жоспар жақынырақ.
Минималды элемент әдісі. Бұл әдістің де алгоритмі қадамдардың соңғы санынан тұрады.
1-кадам. Шығындар матрицасынан минималды элемент табылады:
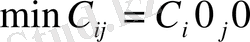
 жоспарының сәйкес элементі анықталады:
жоспарының сәйкес элементі анықталады:
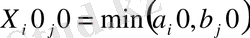
2 жағдай болуы мүмкін:
А)
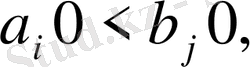 онда
онда
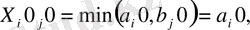 бұл жағдайда А
бұл жағдайда А
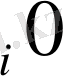 пункті толығымен босаған, сондықтан басқа тұтынушыларға бұл пункттен жүк жіберілмейді, яғни
пункті толығымен босаған, сондықтан басқа тұтынушыларға бұл пункттен жүк жіберілмейді, яғни
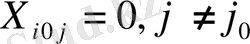 және бөлуші кестенің
және бөлуші кестенің
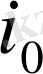 жолы жабылады, ал
жолы жабылады, ал
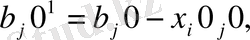 2-қадамға өтелік.
2-қадамға өтелік.
В)
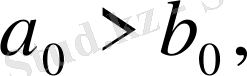 бұл жағдайда
бұл жағдайда
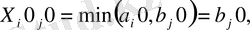 яғни
яғни
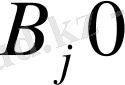 тұтынушының сұранысы толығымен қанағаттандырылды, демек басқа жабдықтаушылардан оған жүк жеткізу қажет емес, сондықтан
тұтынушының сұранысы толығымен қанағаттандырылды, демек басқа жабдықтаушылардан оған жүк жеткізу қажет емес, сондықтан
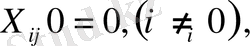 яғни бастапқы тірек жоспардың
яғни бастапқы тірек жоспардың
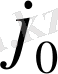 -ші бағаны аныкталды. Мұнда бөлуші кестедегі
-ші бағаны аныкталды. Мұнда бөлуші кестедегі
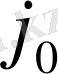 -ші баған жабылады, ал
-ші баған жабылады, ал
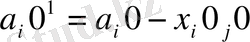 2-қадамға өтелік.
2-қадамға өтелік.
2-қадам. 1-қадамда бастапқы тірек жоспардың жолын немесе бағанын анықтағаннан кейін, сәйкес жол немесе баған сызылғаннан кейін қалған бөлуші кестеде тағы да транспорттық шығындардың минималды элементін іздейміз
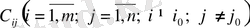 1-қадамдағы секілді жоспардың сәйкес элементі анықталады және т. б. Осы процесті жалғастыра отырып, қадамдардың соңғы санына карай бастапқы жоспарды анықтай аламыз.
1-қадамдағы секілді жоспардың сәйкес элементі анықталады және т. б. Осы процесті жалғастыра отырып, қадамдардың соңғы санына карай бастапқы жоспарды анықтай аламыз.
Теорема. Минималды элемент әдісімен алынған жоспар тірек жоспар болып табылады. (3 - кесте) . Мысалы: a
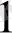 =15, a
=15, a
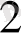 =16, a
=16, a
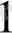 =17
=17
 b
b
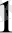 =11, b
=11, b
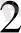 =12, b
=12, b
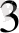 =12, b
=12, b
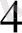 =13
=13
Тапсырманың шешімділігі алдын ала анытқталған. Тірек жоспарды минималды элемент әдісімен анықталық. Бөлуші кесте құрамыз:
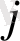 a
a
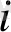
0
11
10
12
0
6
12
0
13
3 - кесте. Минималды элемент әдісімен алынған тірек жоспар
1-қадам. Транспорттық шығындар арасынан минималды элементті табамыз:
min
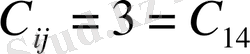 Equation. 3
Equation. 3
Х
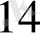 жоспарының бөлуші кестенің бірінші жолында және соңғы бағанында орналасқан сәйкес элементін анықтаймыз:
жоспарының бөлуші кестенің бірінші жолында және соңғы бағанында орналасқан сәйкес элементін анықтаймыз:
X
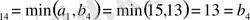 Equation. 3
Equation. 3
Көріп тұрғанымыздай, 4-ші тұтынушының сұранысы толығымен қанағаттандырылды, сондықтан
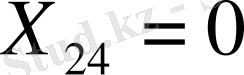 , ал
, ал
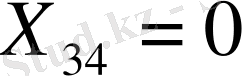 және бөлуші кестенің 4-ші бағаны жабылады, мұнда a
және бөлуші кестенің 4-ші бағаны жабылады, мұнда a
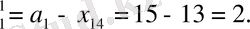 Equation. 3 2-қадамға өтелік.
Equation. 3 2-қадамға өтелік.
2-қадам. 4-ші бағанды сызып тастағаннан кейін қалған бөлуші кестеде транспорттық шығындардың минималды элементін іздейміз - С
31
= 3. Жоспардың сәйкес элементін анықтаймыз:
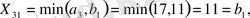 сонда
сонда
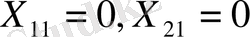 және бөлуші кестенің бірінші бағаны жабылады, ал
және бөлуші кестенің бірінші бағаны жабылады, ал
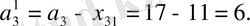 3-кадамға өтеміз.
3-кадамға өтеміз.
3-қадам. Сызылғаннан кейін қалған бөлуші кестеде тағы да транспорттық шығыңдардың минималды элементі анықталады. Олар бірнешеу бодғандықтан, кез келгенін таңдаймыз, мысалы,
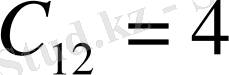 .
Жоспар элементін табайық
.
Жоспар элементін табайық
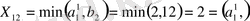 , мұнда
, мұнда
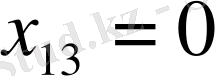 және бөлуші кестенің бірінші жолы жабылады, ал
және бөлуші кестенің бірінші жолы жабылады, ал
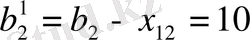 .
.
4-қадам. Бөлуші кестеде 4 торша қалды, оларда транспорттық шығындардың минималды элементін табамыз - С
22
= 4. Х
12
= min (а
2
, ) = min (16, 10) =10=
 анықтаймыз, мұнда
анықтаймыз, мұнда
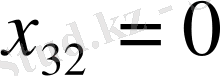 және бөлуші кестенің 2-ші бағаны жабылады, ал а
2
1
= а
2
- х
22
=16-10=6
.
және бөлуші кестенің 2-ші бағаны жабылады, ал а
2
1
= а
2
- х
22
=16-10=6
.
5-қадам. Транспорттық шығындардың келесі минималды элементі - С
33
=4.
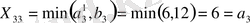 aнықтаймыз, 3-ші жолдың барлық элементтері анықталған, яғни бөлуші кестенің 3-ші жолы жабылады, мұнда тек 3-ші тұгынушы ғана қанағаттандырылмай қалды, оған жүктің 6 бірлігі жетпейді, мұны ол жүктің 6 бірлігі қалған 2-ші жабдықтаушыдан алады.
aнықтаймыз, 3-ші жолдың барлық элементтері анықталған, яғни бөлуші кестенің 3-ші жолы жабылады, мұнда тек 3-ші тұгынушы ғана қанағаттандырылмай қалды, оған жүктің 6 бірлігі жетпейді, мұны ол жүктің 6 бірлігі қалған 2-ші жабдықтаушыдан алады.
6-қадам.
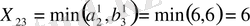 Сонымен, тірек жоспарын аламыз:
Сонымен, тірек жоспарын аламыз:
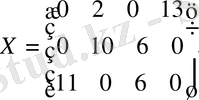
Алынған тасымалдау жоспарына сәйкес келетін шығындарды анықтаймыз. Оларды бөлуші кесте бойынша оңай есептеуге болады:
L(X) =2*4+13*3*+10*4+6*5+11*3+6*4=8+39+40+30+33+24=174
Егер енді минималды элемент және солтүстік-батыс бұрыш әдістерімен алынған жоспарлардың транспорттық шығындарын салыстырып көрер болсақ, онда минималды элемент тәсілі арқылы үздік тірек жоспары алынғандығын көруге болады.
1. 4 Транспорттық тапсырманың тірек жоспарының оңтайлылық өлшемі.
Әрбір А
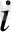 жіберу пунктіне сәйкесінше
жіберу пунктіне сәйкесінше
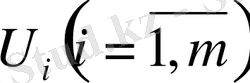 шамаларын қоямыз, ал әрбір тұтыну пунктіне -
шамаларын қоямыз, ал әрбір тұтыну пунктіне -
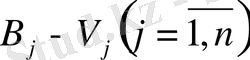 . Потенциалдар деп аталатын бұл шамаларда мынадай шарттар орындалады:
. Потенциалдар деп аталатын бұл шамаларда мынадай шарттар орындалады:
жоспардың нөлдік емес компоненттері үшін

Шамаларды анықтаймыз:
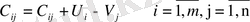
Бұлардан
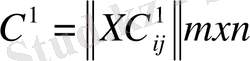 матрицасын құрамыз.
матрицасын құрамыз.
Матрица
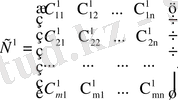
X=
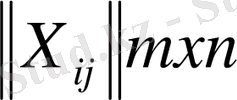 жоспарының бағалаушы матрицасы деп аталады.
жоспарының бағалаушы матрицасы деп аталады.
Сонда транспорттык, тапсырма жоспарының оңтайлылық
өлшемі төмендегі теорема түрінде беріледі.
Теорема. X=
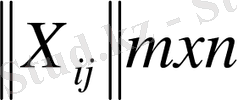 жоспары оңтайлы болу үшін оның бағалаушы матрицасының барлық элементтері теріс емес болуы қажет және жеткілікті, яғни:
жоспары оңтайлы болу үшін оның бағалаушы матрицасының барлық элементтері теріс емес болуы қажет және жеткілікті, яғни:
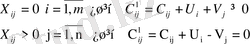
2. ЖҮК ТАСЫМАЛДАУ ЕСЕБІН ПОТЕНЦИАЛДАР ӘДІСІМЕН ШЕШУ
2. 1 Алғашқы таяныш шешімді анықтау тәсілдері
Тасымалдау есебі де сызықты бағдарламалау есебіне жатады, оны шешу үшін кәдімгі симплекс әдісін пайдалануға болады. Бірақ бұл есепті шешу үшін арнайы потенциалдар әдісі қолданылады.
Потенциалдар әдісін қолдану үшін тасымалдау есебінің тек жабық моделі қарастырылады.
Сондықтан тасымалдау есебінің төмендегі моделін қарастырамыз:
жүк тасымалдау есебінің мағнасы - А 1 , А 2 , . . . , А m қоймаларындағы жүкті В 1 , В 2 , . . . , В n тұтынушыларға апарудың тиімді жоспарын құруда.
Бұл есептерді оның құндық белгісі және уақыт белгісіне байланысты екі түрге бөлуге болады. Бірінші жағдайда оның тиімді жоспары - орындалуына минималды қаржы жұмсауда, ал екінші жағдайда - оған аз уақыт жұмсау.
а 1 , а 2 , . . . , а m әріптерімен саны m-ге тең А 1 , А 2 , . . . , А m қоймаларындағы сәйкес жүктердің мөлшерін, ал а әрпімен жүктің жалпы мөлшерін
а 1 + а 2 + . . . + а m = а (11)
белгілейік.
В 1 , В 2 , . . . , В n тұтынушыларына қажетті жүк мөлшерлерін в 1 , в 2 , . . . , в n , ал барлық қажетті жүк мөлшерін в әрпімен
в 1 + в 2 + . . . + в n = в (12)
белгілейік.
Егер де қоймалардағы жүктердің жалпы мөлшері тұтынушыларға қажетті жүктің мөлшеріне тең болса, яғни
а = в, (13)
онда бүл жүк тасымалдау есебінің жабық моделі деп аталады. Ал а ≠ в жағдайда есеп ашық модель болып табылады.
(11) және (12) шарттарға қосымша тарифтер матрицасы Сi j берілген, олар бірлік жүкті Аi пунктінен Вә пунктіне апаруға кететін жол ақысын көрсетеді. Жүк тасудың ең аз шығын жұмсалатындай жоспарын құру қажет.
x ij арқылы А i пунктінен В j тұтынушыға тасылатын жүктің мөлшерін белгілейміз. Бұл шамалар жиыны тасу матрицасын көрсетеді.
Қойылған есептің экономика-математикалық моделі төмендегідей болады:
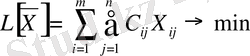 (14)
(14)
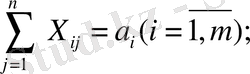 (15)
(15)
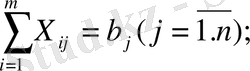 (16)
(16)
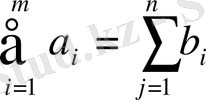 (17)
(17)
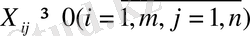 (18)
(18)
Тасымалдау есебінің алғашқы таяныш шешімін анықтау әртүрлі жолмен орындалуы мүмкін. Олардың ең көп тараған түрлері:
а) диогональды
және
в) ең кіші элемент
тәсілдері.
Диогональды тәсіл боцынша тасымалдау есебінің үлестіру кестесі оның жоғарғы сол жақ бұрышынан бастап толтырылады (4 - кесте) . Мұндағы негізгі ереже (15) және (16) теңдіктерінің орындалуында.
жүк
қоры
8
0
2
110
8
0
3
40
6
0
2
100
8
0
4
10
7
0
6
130
4
0
3
0
2
80
4
60
8
0
4 - кесте. Тасымал кестесі
Бұл тасымалдау кестесінің толтырылу тәртібі төмендегідей:
алдымен ең жоғарғы сол жақтағы бұрыштағы кереге көзге 100 деген сан жазылады; оның себебі А 1 қоймасында 150 мөлшерінде жүк қоры болса, ал В 1 пайдалануға қажеті 100; сондықтан х 11 =100. Одан артылған 50 мөлшердегі жүк екінші тұтынушыға жіберіледі, немесе х 12 =50, ал қалғандары бірінші қоймадан жүк алмайды, немесе х 13 =х 14 =х 15 =0. Сонымен бірінші тұтынушы В 1 өз қажеттілігін толық қамтамасыз еткендіктен басқа қоймадан жүк алмайды, немесе х 21 =х 31 =0.
Осыдан кейін келесі толтырылатын кереге көз екінші жатық жол мен екінші тік жолдың қиылысында орналасқан. Мұнда екінші тұтынушы В 2 -ге қажетті 60 мөлшердегі жүк берілуге жиіс немесе х 22 =60. Сонда ол өз қажетілігін түгел қамтамасыз етеді, немесе х 32 =0.
Осылайша қайталана отырып, кестенің барлық торларын толтыруға болады. Сонымен (15) -(18) шарттарын қанағаттандыратын мынандай шешім немесе тасымалдау жоспарын құрастыруға болады:
х11 = 100; х 12 =50; х 13 =0; х 14 =0; х15 = 0;
х21 = 0; х22 = 60; х23 = 90; х24 = 90; х25 = 0;
х31 = 0; х32 = 0; х33 = 0; х34 = 10; х35 = 130;
Бұл жоспарды орындауға жұмсалатын қаржы мөлшері былайша анықталады:
F= 8*100 + 2*50+ 8*60+ 4*90+ 7*90+ 4*10+ 8*130=3450
2. 2 Ең кіші элемент тәсілі
Жоғарыда қарастырылған тәсіл бойынша үлестіру кезінде тасымалдауға жұмсалатын қаржы есепке алынбайды. Ол үшін ең кіші элемент тәсілін пайдалануға болады. Ең кіші элемент тәсілі бойынша кестені ең кіші элемент орналасқан тор көзін толтырудан бастаймыз (5 - кесте) . Ал қалғандары жоғарыда көрсетілген тәсілдегі (15) -(18) шарттарының орындалуын қамтамасыз етуге тиіс.
Жоғарыдағы мысалды қарастырайық.
8
0
2
110
8
0
3
40
6
0
2
100
8
0
4
10
7
0
6
130
4
0
3
0
2
80
4
60
8
0
5 - кесте. Ең кіші элемент тәсілі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz