Компьютерлік қосымшалар арқылы есептеу әдістері: теория, алгоритмдер және Delphi-де жүзеге асыру


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:
Компьютерлік қосымшамен есептеу әдістері
Мазмұны
1. Кіріспе
2. Жалпы теориялық мағлұмат
3. Есептің математикалық шығарылуы
3. 1. Бірінші тапсырманың математикалық түрі.
3. 2. Екінші тапсырманың математикалық түрі.
3. 3. Үшінші тапсырманың математикалық түрі.
3. 4 Төртінші тапсырманың математикалық түрі.
3. 5. Бесінші тапсырманың математикалық түрі.
3. 6. Алтыншы тапсырманың математикалық түрі.
4. Алгоритм
5. Delphi ортасында өңделген программаның тексті
5. 1. Бірінші тапсырманың программасы
5. 2. Екінші тапсырманың программасы
5. 3. Үшінші тапсырманың программасы
5. 4 Төртінші тапсырманың программасы
5. 5. Бесінші тапсырманың программасы.
5. 6. Алтыншы тапсырманың программасы
6. Программалардың нәтижесі
7. Есептердің шыққан нәтижесін программалық қосымшамен (MathCad) салыстыру
8. Блок-схемалар
9. Қорытынды
10. Әдебиеттер тізімі
Кіріспе
Соңғы елу жыл ішінде ЭЕМ (электронды есептеу машиналары) даму дәуірінде көптеген өзгерістер болды. Алғашқы шамды ЭНИАК есептеуіш техникасынан бастап бүгінгі күні дербес компьютерлерге дейінгі ЭЕМ дамуын төрт сатуға бөлуге болады.
Бірінші сатыға бізге белгілі алғашқы сериалды шамды БЭСМ-1, “Стрела” есептеуіш машиналарынан бастап 60-шы жылдарға дейінгі ЭЕМ-дерді жатқызуға болады. Бірінші сатыдағы ЭЕМ-дер қатарына: БЭСМ-1, БЭСМ-2, Стрела, Минск-1, М-20 жатады. Бұл ЭЕМ-дер есептеу барысында бір секундта оншақты мыңдай амал орындай алаған.
Екінші сатыға - транзисторлы есептеуіш машиналары жатады (секундына 100 мыңдай амал орындайды) . Екінші сатыдағы ЭЕМ-дер қатарына кіші есептеуіш машиналар (Минск сериалы) Урал типті машиналар және БЭСМ-6 жатады.
Үшінші сатыға - интегралдық жүйеге негізделген есептеуіш комплекстер жатады (секундына миллиондай амал орындайды) . Осы сатының машиналары бірлесіп қызмет істей алатын немесе біріккен жүйенің ЭЕМ-дерді қатарына ЕС ЭЕМ (IBM 360/370) сериасымен жасалып шыққан есептеу комплекстері кіреді (секундына оншақты миллион амал орындайды) .
ЭЕМ-нің қолданылатып жерлері өте көп. Олар физикалық процестерді модельдеу (мәселен, ауа-райын болжау), биологиялық процестерді зерттеу, автоматты түрде жобалау жұмыстарын жүргізу, вокзалдардағы анықтама бюросының қызметін атқару, автоматты түрде билеттерді сату жұмыстарын ойдағыдай атқарып келеді.
Қазіргі уақытта ғылыми техниканың дамудың жетістіктеріне сай, алдыңғы қатарлы ЭЕМ - өміріміздің әралуан саласында кеңінен қолданылуда. Осыған орай - ЭЕМ-да жұмыс істеу реттерін программа арқылы басқара алатын систематехника инженерлеріне сұраныс көп. ЭЕМ-сы мен арақатынасын қалыптастыруға керекті алгоритмдік тілдер: Фортран, Паскаль, Бейсик, Си, Дельфи, т. б., компьютерде есептерді белгілеп, нәтижесін шығаруға бейімделген.
Ғылым мен техникада көптеген есептер функциялалар, алгебралық, дифференциалдық немесе интегралдық теңдеулер арқылы математика тілінде сипатталып жазылады. Мұндай есептер бірнеше жолдармен шешіледі. Анализдік әдістер сондай жолдардың бірі болып табылады. Бірақ оларды пайдалану көп жағдайда мүмкін бола бермейді.
Есептеу кезінде анализдік әдістерді пайдалану қиындық келтіргенде немесе тіпті пайдалану мүмкін болмаған жағдайда есептеу математикасының сандық әдістері қолданылады. Ол әдістер бастапқы берілген есепті мағынасы бойынша соған жуық басқа есеппен алмастыру мүмкіндігіне негізделген. Ал соңғы есеп кейбір шарттарды қанағаттандыру тиіс. Мысалы, шешімнің бар болуы, орнықты, жинақты болуы және т. с. с. Бұл есептің алғашқы есптің жуық шешімін беруі тиіс немесе оған белгілі бір дәлдікпен жинақталу қажет.
Есепте негізгі деректер, яғни ондағы коэффиценттер, бос мүшелер немесе қосымша шарттар жуық шамалармен берілу мүмкін, соның нәтижесінде пайда болған қателіктерді жөнделінбейтін қателіктер деп аталады.
ЭЕМ-де цифрлар саны шексіз көп сандарға арифметикалық амалдар қолданылмайды. Сондықтан ондай сандар ең алдымен цифрларының саны шектеулі жуық сандармен алмастырылады. Осындай дөңгелектеулердің сандарынан пайда болған қателіктерді есептік қателіктер деп атайды. Олар есептің жуық шешімнің дәлдігіне тікелей әсерін тигізетіні анық.
Алгоритм деп берілген деректердің дәйекті нәтижеге түрлену жолын көрсететін ережелер мен нұсқаулар жүйесін айтады.
Алгоритмның келесі қасиеттері бар:
а) Есептің шығару (шешу) жолын бір мағыналы түрде анықтау;
ә) Мүмкіндігінше есептің әр түрлі варианттарын шығаруға жағдай туғызу;
б) Қолдану барысында белгілі бір заңдылық бойынша есептеу нәтижесін міндетті түрде жеткізу;
Керек болған жағдайда алгоритмге сәйкес блок-схема жасалады.
Блок-схема - алгоритмның орындауын ұйымдастыру үшін қолданылатын амалдар тізбегінің графиктік кескіні.
Блок-схема келісілген геометриялық фигуралардың көмегімен құралады және бұл фигураларға келісімге байланысты өзіндік мағыналар беріледі. Мәселен, тіктөртбұрыш - арифметикалық амалдарды орындаушы блок, ромбыны - кезөкелген шартты тексеруші немесе салыстыру процесін орындаушы блок, ал эллипс және параллелограм тәрізді фигураны енгізу және қорытындылау процестерін жүргізуші блоктар ретінде пайдалануға болады. Бұл фигуралар алгоритмның мазмұнына сәйкес өзара сызықтар арқылы жалғасады.
Әрбір фигура ішінде орындалатын амалдар көрсетіледі де, олар амалдар блогы деп аталады. Блок-схеманы жасағанда басқа да геометриялық фигураларды пайдалануға болады.
2 Жалпы теориялық мағлұмат
Қарапайым алгебралық теңдеулердің түбірлерін жуықтап есептеу әдістері. Кейбір қарапайым теңдеулердің түбірлері жай математикалық жолмен табу қиынға түседі. Сол себептен ондай теңдеудің түбірлерін арнайы математикалық әдістермен табамыз.
Итерация:
f(x) =0 (1), ол (-∞, ∞) f(x) функциясы мына аралықта үзіліссіз және бұл аралықта f(x) функциясының бір түбірі бар деп есептейміз. Түрлендіреміз →f(x) ⇒x=ϕ(x) ; (2) [a, b] аралық;
x 0 - мына аралықта (-∞, ∞) жатқан қандай да бір сан. X 0 =a;
x 0 -ді осы функцияның алғашқы мәні деп алып, мына теңдеуге қоямыз x 1 =ϕ(x 0 ) ; x 2 =ϕ(x 1 ) ;
Жалпы формуласы: x n =ϕ(x n-1 ) ; n=1, 2, 3…
Тоқтату шарты:
X n -X n-1 <=e , e=0. 001;
Ньютон:
f(x) =0 функциясы берілсін. [a, b] аралықта үздіксіз және анықталған болсын. Сол сияқты бұл аралықта
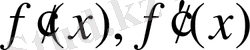 -функциялары үздіксіз.
-функциялары үздіксіз.
X
0
бастапқы мәнін табу керек. Ол үшін берілген теңдеудің 1 және 2 туындысын табу керек.
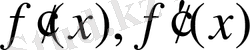 -?Алғашқы X
0
- мәні келесі шарт арқылы табылады.
-?Алғашқы X
0
- мәні келесі шарт арқылы табылады.
Шарт:
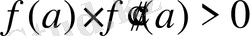 онда x
0
=a;
онда x
0
=a;
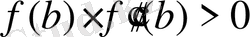 онда x
0
=b;
онда x
0
=b;
Сөйтіп алғашқы мәнді анықтағаннан кейін х-тің келесі мәндерін есептейміз.
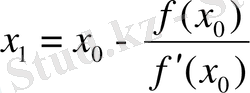
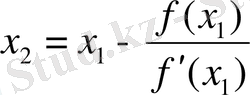
Ал Ньютон әдісін есептеудің жалпы формуласы келесі түрде өрнектеледі:
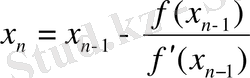
Тоқтату шарты:
X n -X n-1 <=e , e=0. 001;
Хорда:
X 0 =a; Жалпы формуласы келесі түрде өрнектеледі:
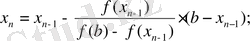
Тоқтату шарты:
X n -X n-1 <=e , e=0. 001;
Биссекция:
Бұл есепті екі аралықты бөлу арқылы есептептейміз. Шарт қанағаттандырылған кезде есептің мәні шығады.
c=(a+b) /2 if f(c) <e then X:=c if f(a) *f(c) >0 then a:=c else b:=c
Симпсон, Трапеция әдістері.
Симпсон, Трапеция әдістері интегралды жуықтап есептеуге арналған.
Трапеция формуласы [a, b] интегралдау кесіндісін тең бөліктерге бөлуді қажет етеді. X 0 =a; X n =b; Оның жалпы формуласы:
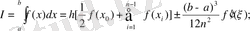
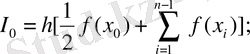
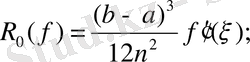 Equation. 3
Equation. 3
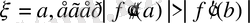
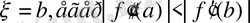
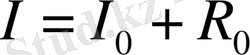
Симпсон формуласы [a, b] интегралдау кесіндісін n=2 m бөліктерге бөлу үшін жазылады. Оның жалпы формуласы:
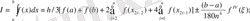
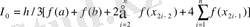
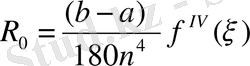 ,
,
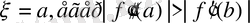
4 Алгоритм:
4. 1. 1-ші тапсырманың алгоритмі
1. Бағдарлама мәтіні
2. Типтерді яғни компоненттерді анықтау процедурасы
3. Айнымалыларды анықтау процедурасы
4. Ньютон әдісінің негізгі формуласын анықтау
5. Итерация әдісінің негізгі формуласын анықтау
6. Биссекция әдісінің негізгі формуласын анықтау
7. Хорда әдісінің негізгі формуласын анықтау
8. Компоненттерді тазалау процедурасы
9. Бағдарламаның соңы
4. 2 2-ші тапсырманың алгоритмі
1. Бағдарлама мәтіні
2. Типтерді яғни компоненттерді анықтау процедурасы
3. Айнымалыларды анықтау процедурасы
4. Гаусс әдісінің негізгі формуласын анықтау
5. Зейдель әдісінің негізгі формуласын анықтау
6. Компоненттердің байланыстыру мен жасыру процедурасы
7. Бағдарламаның соңы
- 3-ші тапсырманың алгоритмі
1. Бағдарлама мәтіні
2. Типтерді яғни компоненттерді анықтау процедурасы
3. Айнымалыларды анықтау процедурасы
4. Ньютон әдісінің негізгі формуласын анықтау
5. Итерация әдісінің негізгі формуласын анықтау
6. Компоненттерді тазалау процедурасы
7. Бағдарламаның соңы
4. 4. 4-ші тапсырманың алгоритмі
1. Бағдарлама мәтіні
2. Типтерді яғни компоненттерді анықтау процедурасы
3. Айнымалыларды анықтау процедурасы
4. Ньютон әдісінің негізгі формуласын анықтау
5. Кері Ньютон әдісінің негізгі формуласын анықтау
6. Лагранж әдісінің негізгі формуласын анықтау
7. Компоненттерді тазалау процедурасы
8. Бағдарламаның соңы
4. 5 5-ші тапсырманың алгоритмі
1. Бағдарлама мәтіні
2. Типтерді яғни компоненттерді анықтау процедурасы
3. Айнымалыларды анықтау процедурасы
4. Симпмон әдісінің негізгі формуласын анықтау
5. Трапеция әдісінің негізгі формуласын анықтау
6. Бағдарлама нәтижесін шығару процедурасы
4. 6 6-ші тапсырманың алгоритмі
1. Бағдарлама мәтіні
2. Типтерді яғни компоненттерді анықтау процедурасы
3. Айнымалыларды анықтау процедурасы
4. Эйлер әдісінің негізгі формуласын анықтау
5. Бағдарлама нәтижесін шығару процедурасы
5. Delphi ортасында өңделген программаның тексті
5. 1. Бірінші тапсырманың программасы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Memo1: TMemo;
Memo2: TMemo;
Memo3: TMemo;
Memo4: TMemo;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
RadioButton3: TRadioButton;
RadioButton4: TRadioButton;
Edit1: TEdit;
Edit2: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
BitBtn1: TBitBtn;
procedure RadioButton1Click(Sender: TObject) ;
procedure RadioButton2Click(Sender: TObject) ;
procedure RadioButton3Click(Sender: TObject) ;
procedure RadioButton4Click(Sender: TObject) ;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
a, b, x, eps:real; k:integer;
implementation
{$R *. dfm}
procedure TForm1. RadioButton1Click(Sender: TObject) ;
var j, y:real;
begin
a:=strtoint(edit1. Text) ;
b:=strtoint(edit2. Text) ;
k:=0; eps:=0. 001;
repeat
x:=(a+b) /2;
y:=22*x*x*x+7*x-1;
if y>0 then b:=x else a:=x;
k:=k+1;
j:=abs(b-a) ;
memo1. Lines. Add('x='+floattostr(x) +'k='+inttostr(k) ) ;
until j<eps
end;
procedure TForm1. RadioButton2Click(Sender: TObject) ;
var j, y, y1, za, zB, z2a, z2b, m:real;
begin
a:=strtoint(edit1. Text) ;
b:=strtoint(edit2. Text) ;
k:=0; eps:=0. 001;
za:=22*a*a*a+7*a-1;
zb:=22*b*b*b+7*b-1;
z2a:=132*a;
z2b:=132*b;
if za*z2a>0 then x:=a else x:=b;
repeat
y:=22*x*x*x+7*x-1;
y1:=66*x*x+7;
m:=x-(y/y1) ;
k:=k+1;
j:=abs(m-x) ;
x:=m;
memo2. Lines. Add('x='+floattostr(x) +'k='+inttostr(k) ) ;
until j<eps;
end;
procedure TForm1. RadioButton3Click(Sender: TObject) ;
var j:real;
begin
a:=strtoint(edit1. Text) ;
b:=strtoint(edit2. Text) ;
k:=0;
repeat
x:=exp(1/3*ln(abs((1-7*a) /22) ) ) ;
k:=k+1;
j:=abs(x-a) ;
a:=x;
memo3. Lines. Add('x='+floattostr(x) +'k='+inttostr(k) ) ;
until j<0. 001;
end;
procedure TForm1. RadioButton4Click(Sender: TObject) ;
var j, zb, y:real;
begin
a:=strtoint(edit1. Text) ;
b:=strtoint(edit2. Text) ;
k:=0; eps:=0. 001;
zb:=22*b*b*b+7*b-1;
repeat
y:=22*a*a*a+7*a-1;
x:=a-(y/(zb-y) ) *(b-1) ;
k:=k+1;
j:=abs(x-a) ;
a:=x;
memo4. Lines. Add('x='+floattostr(x) +'k='+inttostr(k) ) ;
until j<eps
end;
end.
5. 2. Екінші тапсырманың программасы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
Memo1: TMemo;
Memo2: TMemo;
BitBtn1: TBitBtn;
procedure RadioButton1Click(Sender: TObject) ;
procedure RadioButton2Click(Sender: TObject) ;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *. dfm}
procedure TForm1. RadioButton1Click(Sender: TObject) ;
var a11, a12, a13, a14, a21, a22, a23, a24, a31, a32, a33, a34, a41, a42, a43, a44:real;
b1, b2, b3, b4, x, y, z, s, q, w, e, k, l, x1, x2, x3, x4:real;
begin
a11:=1. 7; a12:=-1. 8; a13:=1. 9; a14:=-57. 4; b1:=10;
a21:=1. 1; a22:=-4. 3; a23:=1. 5; a24:=-1. 7; b2:=19;
a31:=1. 2; a32:=1. 4; a33:=1. 6; a34:=1. 8; b3:=20;
a41:=7. 1; a42:=-1. 3; a43:=-4. 1; a44:=5. 2; b4:=10;
x:=a12/a11; y:=a13/a11; z:=a14/a11; s:=b1/a11;
a22:=a22-a21*x; a32:=a32-a31*x; a42:=a42-a41*x;
a23:=a23-a21*y; a33:=a33-a31*y; a43:=a43-a41*y;
a24:=a24-a21*z; a34:=a34-a31*z; a44:=a44-a41*z;
b2:=b2-a21*s; b3:=b3-a31*s; b4:=b4-a41*s;
q:=a23/a22; w:=a24/a22; e:=b2/a22;
a33:=a33-a32*q; a43:=a43-a42*q;
a34:=a34-a32*w; a44:=a44-a42*w;
b3:=b3-a32*e; b4:=b4-a42*e;
k:=a34/a33; l:=b3/a33;
a44:=a44-a43*k; b4:=b4-a43*l; x4:=b4/a44; x3:=l-k*x4;
x2:=e-q*x3-w*x4; x1:=s-x*x2-y*x3-z*x4;
memo1. Lines. Add('x1='+floattostr(x1) ) ;
memo1. Lines. Add('x2='+floattostr(x2) ) ;
memo1. Lines. Add('x3='+floattostr(x3) ) ;
memo1. Lines. Add('x4='+floattostr(x4) ) ;
end;
procedure TForm1. RadioButton2Click(Sender: TObject) ;
var a11, a12, a13, a14, a21, a22, a23, a24, a31, a32, a33, a34, a41, a42, a43, a44:real;
b1, b2, b3, b4, x01, x02, x03, x04, x1, x2, x3, x4, h, e, k, l, eps:real;
p:integer;
begin
eps:=0. 0001;
a11:=1. 7; a12:=-1. 8; a13:=1. 9; a14:=-57. 4; b1:=10;
a21:=1. 1; a22:=-4. 3; a23:=1. 5; a24:=-1. 7; b2:=19;
a31:=1. 2; a32:=1. 4; a33:=1. 6; a34:=1. 8; b3:=20;
a41:=7. 1; a42:=-1. 3; a43:=-4. 1; a44:=5. 2; b4:=10;
x01:=b1/a11; x02:=b2/a22; x03:=b3/a33; x04:=b4/a44;
p:=0;
repeat
x1:=(b1-2*x02-a13*x03-a14*x04) /a11;
e:=abs(x1-x01) ;
x01:=x1;
x2:=(b2-1*x01-a23*x03-a24*x04) /a22;
k:=abs(x2-x02) ;
x02:=x2;
x3:=(b3-1*x01-a32*x02-a34*x04) /a33;
l:=abs(x3-x03) ;
x03:=x3;
x4:=(b4-1*x01-a42*x02-a43*x03) /a44;
h:=abs(x4-x04) ;
x04:=x4;
p:=p+1;
memo2. Lines. Add('p='+floattostr(p) ) ;
memo2. Lines. Add('x1='+floattostr(x1) +' x2='+floattostr(x2) ) ;
memo2. Lines. Add('x3='+floattostr(x3) +' x4='+floattostr(x4) ) ;
until (e<eps) and (k<eps) and (l<eps) and (h<eps) ;
end;
end.
5. 3. Үшінші тапсырманың программасы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Memo1: TMemo;
Memo2: TMemo;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
BitBtn1: TBitBtn;
procedure RadioButton1Click(Sender: TObject) ;
procedure RadioButton2Click(Sender: TObject) ;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
var x0, y0, x1, y1, j1, l1, q1, w1:real;
a, k:integer;
{$R *. dfm}
function f(x, y:real) :real;
begin
f:=1/4*sin((20*y) /3) +2
end;
function fy(x, y:real) :real;
begin
fy:=20;
end;
function fx(x, y:real) :real;
begin
fx:=0
end;
function G(x, y:real) :real;
begin
G:=1/2*cos(x/4) ;
end;
function Gx(x, y:real) :real;
begin
Gx:=1;
end;
function Gy(x, y:real) :real;
begin
Gy:=0;
end;
procedure TForm1. RadioButton1Click(Sender: TObject) ;
begin
x0:=3. 5;
y0:=2. 5;
if(abs(5/3*cos(20/3*y0) ) <1) and(abs(-1/8*sin(x0/4) ) <1) then begin
repeat
x1:=1/4*sin(20/3*y0) +3;
y1:=1/2*cos(x0/4) ;
k:=k+1;
j1:=x1-x0;
l1:=y1-y0;
x0:=x1;
y0:=y1;
memo1. Lines. Add('k='+inttostr(k) ) ;
memo1. Lines. Add('x1='+floattostr(x1) ) ;
until(abs(j1) <0. 0001) and (abs(l1) <0. 0001) end
else memo1. lines. Add('shart orindalmaidi') ;
end;
procedure TForm1. RadioButton2Click(Sender: TObject) ;
label 3;
var h0, h, k0, k, I, I0, :real;
begin
n:=0;
3: I0:=fx(x0, y0) *Gy(x0, y0) -Gx(x0, y0) *fy(x0, y0) ;
h0:=-1/I0*(f(x0, y0) *Gy(x0, y0) -G(x0, y0) *fy(x0, y0) ) ;
k0:=-1/I0*(fx(x0, y0) *G(x0, y0) -Gx(x0, y0) *f(x0, y0) ) ;
x:=x0+h0;
y:=y0+k0;
if(abs(x-x0) <=e) or(abs(y-y0) <=e) then
begin
memo1. Lines. Add('x='+floattostr(x) ) ;
memo1. Lines. Add('y='+floattostr(y) ) ;
end
else
begin
x0:=x;
y0:=y;
I0:=I;
h0:=h;
k0:=k;
n:=n+1;
goto 3;
end;
memo1. Lines. Add('kadami='+inttostr(n) ) ;
memo1. Lines. Add('I0='+floattostr(I0) ) ;
memo1. Lines. Add('k0='+floattostr(k0) ) ;
memo1. Lines. Add('h0='+floattostr(y0) ) ;
end;
end.
5. 4 Төртінші тапсырманың программасы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Memo1: TMemo;
Memo2: TMemo;
Memo3: TMemo;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
RadioButton3: TRadioButton;
BitBtn1: TBitBtn;
procedure RadioButton1Click(Sender: TObject) ;
procedure RadioButton2Click(Sender: TObject) ;
procedure RadioButton3Click(Sender: TObject) ;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *. dfm}
var x0, x1, x2, x3:integer;
x, n1, n2, l, l03, l13, l23, l33, l0, l1, l2, l3, y01, y12, y23, y012, y123, y0123:real;
y10, y21, y32, y210, y321, y3210:real;
y0, y1, y2, y3:integer;
procedure TForm1. RadioButton1Click(Sender: TObject) ;
begin
x:=-3. 25;
x0:=-4; x1:=-3; x2:=-2; x3:=-1;
y0:=-60; y1:=-20; y2:=0; y3:=140;
y01:=(y1-y0) /(x1-x0) ;
y12:=(y2-y1) /(x2-x1) ;
y23:=(y3-y2) /(x3-x2) ;
y012:=(y12-y01) /(x2-x0) ;
y123:=(y23-y12) /(x3-x1) ;
y0123:=(y012-y123) /(x3-x0) ;
N1:=y0+(x-x0) *y01+(x-x0) *(x-x1) *y012+(x-x0) *(x-x1) *(x-x2) *y0123;
memo1. Lines. Add('N='+floattostr(n1) ) ;
end;
procedure TForm1. RadioButton2Click(Sender: TObject) ;
begin
x:=-3. 25;
x0:=-4; x1:=-3; x2:=-2; x3:=-1;
y0:=-60; y1:=-20; y2:=0; y3:=140;
y10:=(y0-y1) /(x0-x1) ;
y21:=(y1-y2) /(x1-x2) ;
y32:=(y2-y3) /(x2-x3) ;
y210:=(y10-y21) /(x0-x2) ;
y321:=(y21-y32) /(x1-x3) ;
y3210:=(y210-y321) /(x0-x3) ;
N2:=y3+(x-x3) *y32+(x-x3) *(x-x2) *y321+(x-x3) *(x-x2) *(x-x1) *y3210;
memo2. Lines. Add('N='+floattostr(n2) ) ;
end;
procedure TForm1. RadioButton3Click(Sender: TObject) ;
begin
x:=-3. 25;
x0:=-4; x1:=-3; x2:=-2; x3:=-1;
y0:=-60; y1:=-20; y2:=0; y3:=140;
l03:=((x-x1) *(x-x2) *(x-x3) ) /((x0-x1) *(x0-x2) *(x0-x3) ) ;
l13:=((x-x2) *(x-x3) *(x-x0) ) /((x1-x2) *(x1-x0) *(x1-x3) ) ;
l23:=((x-x1) *(x-x3) *(x-x0) ) /((x2-x1) *(x2-x0) *(x2-x3) ) ;
l33:=((x-x1) *(x-x2) *(x-x0) ) /((x3-x1) *(x3-x2) *(x3-x0) ) ;
l0:=l03*y0;
l1:=l13*y1;
l2:=l23*y2;
l3:=l33*y3;
l:=l0+l1+l2+l3;
memo3. Lines. Add('l='+floattostr(l) ) ;
end;
end.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz