Дисперсті жүйелерді тұрақтандыруды анықтау әдістері

Пән: Химия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

Жоспар

І. Кіріспе . . . 2

ІІ. Негізгі бөлім

2. 1. Дисперсті жүйелердің тұрақтылығы туралы жалпы түсінік . . . 3

2. 2. Дисперсті жүйелерді тұрақтандыруды анықтау әдістері . . . 3 - 8

Дисперсті жүйелердің тұрақсыздығы . . . 9

ІІІ. Қорытынды . . . 10

Пайдаланылған әдебиеттер . . . 11

Кіріспе

Дисперсті жүйелердің тұрақтылығы дегеніміз - оның негізгі көрсеткіштерінің белгілі бір уақыт аралығында дисперсті ортадағы дисперсті фаза бөлшектерінің дисперстілігі мен біркелкі таралуының сақтау қабілеті.

Дисперсті жүйелердің тұрақтылығының екі негізгі түрін ажыратуға болады:

Седиментациялық тұрақтылық дегеніміз - ауырлық күші әсерінен тұнбаға түсу кезінде дисперсті фаза бөлшектерінің потенциалды энергияларының төмендеуіне қарсы жүйенің тұрақтылығы.
Агрегаттық тұрақтылық дегеніміз - бөлшектердің фазалық іріленуіне әкелетін процестерге жүйенің қарсы тұру қабілеті.

Агрегаттылыққа қатысты дисперсті жүйелер кинетикалық және термодинамикалық тұрақты болып бөлінеді. Термодинамикалық тұрақты жүйелер гетерогенді босдисперсті жүйенің өздігінен түзілуі нәтижесінде пайда болады.

Дисперсті жүйелерді сонымен қатар:

лиофильді термодинамикалық тұрақты;
лиофобты термодинамикалы тұрақсыз, бірақ кинетикалық тұрғыда тұрақты болып келеді.

Лиофильді жүйелердің термодинамикалық тұрақтылығы тепе - теңдікте болады, қайтымды және өздігінен түзіледі, макрофаздан, сол сияқты шынайы ерітінділерден түзіледі. Лиофильді жүйелер тек ғана бола алады, ал беткі керілу «бөлшек - орта» шекарасында өте аз болуы мүмкін.

Дисперсті жүйенің термодинамикалық тұрақтылығын қамтамасыз ететін беткі керілудің мәні Ребиндер - Щукин қатынасымен анықталады:

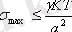
мұндағы γ − өлшемсіз коэффициент;
K - Больцман тұрақтысы;
а - бөлшектің орташа өлшемі.

Есептеулерге қарағанда, лиофильді дисперсті жүйелердегі фазааралық беттік керілу бөлшектердің өлшеміне тәуелді бола отырып мына 1, 4×10 ^-7 - дан 1, 4×10 ^-3 Дж/м ² мәнге ие болады.

Лиофобты жүйелер термодинамикалық тұрақсыз болады, демек, дисперсті фазаның бөлшектері агрегацияға бейім келеді. Олардың агрегативті термодинамикалық тұрақсыздығы энергияның артық мөлшерімен сипатталады.

Седиментация. Гипсометрлік заң. Седиментациялық - диффузиялық тепе - теңдік. Седиментация жылдамдығы.

Ірідисперсті жүйелер гравитациялық күштердің әсерінен тұнбаға түседі (седиментацияға ұшырайды) . Нәтижесінде жүйеде бөлшектердің биіктік бойынша таралуы нақты тепе - теңдікте анықталады. Коллоидтық жүйелер тұрақтылығы бойынша шынайы ерітінділер (мах) және ірідисперсті ерітінділер (min) арасындағы аралық күйде болады.

Дисперсті фазаның әрбір бөлшегіне 3 негізгі күш әсер етеді:

Ауырлық күші Fт
Архимед күші FA
Үйкеліс күші Fтр

Седиментация күші бірінші және екінші күштердің арасында 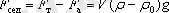нәтижеге ие болады. Егер , F _сед > 0 - болса, онда бөлшектердің тұнбаға түсуі жүреді. Ал егер F _сед < 0 - онда бөлшектер ерітінді бетіне қалқып шығады. Бөлшекке әсер ететін 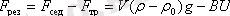мұндағы B - үйкеліс коэффициенті, U - седиментация жылдамдығы, F _сед = F _үйк тепе - теңдік күйде болған жағдайда қорытқы күш болып табылады [1] .

Сфералық бөлшектер үшін үйкеліс күші Стокс заңына сәйкес

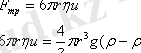
Осыдан бөлшектің радиусы мен тұнбаға түсу жылдамдығы теңдеуі шығады:

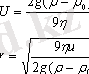
Седиментациялық анализдің қорытындысы болып бөлшектің дәл осы жүйедегі радиус интервалы, жай бөлшектің радиусы немесе анықталған радиустың фракция үлесі болып табылады.

Седиментацияға қабілеттілікті оның жылдамдығы арқылы анықталатын S тұрақтылығымен көрсетеміз:

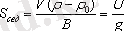
Сфералық бөлшектер үшін константа мынаған тең:

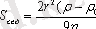
Теңдеуден көріп отырғанымыздай, S мәні бөлшектердің өлшемі, сонымен қатар оның табиғатына да тәуелді болып келеді.

S өлшем бірлігі ретінде 10 ¹³ с сведберг (сб) қабылданған. Көбіне седиментация процесін сипаттау үшін I _сед меншікті ағын шамасы қолданылады.

Седиментацияның меншікті ағыны дегеніміз - седиментацияға қалыпты бағытталған бірлік уақытында көлем қатынасындағы тұнбаға түсетін бөлшектердің саны. Өлшем бірлігі: [ i _сед ] = бөлш/см ² * с.
Бұл анықтамадан i _сед мұнда: i _сед = U _сед * v , мұндағы v - дисперсті жүйедегі бөлшектердің бөлшектік концентрациясы. Бұл теңдеуді U _сед қойып, мына теңдеуді аламыз:

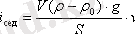
Осылайша, меншікті ағын V , v , ( ρ - ρ _о ) тура пропорционал және S кері пропорционал. Осы формуланы теңдеуге қойсақ, мына теңдеуді аламыз[2] .

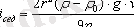Демек, сфералық бөлшектер үшін меншікті ағын радиустың квадратына тура пропорционал және ортаның тұтқырлығына кері пропорционал.

Седиментация процесін қарастыра отырып, біз бөлшектер қатысатын броундық қозғалысты есепке алмаймыз. Броундық қозғалыстың салдары болып табылатын диффузия құбылысы барлық көлемі бойынша бөлшектердің концентрациясын түзетуге ұмтылады, сол кезде седиментация төменгі қабаттағы концентрацияның ұлғаюына әкеледі.

Осылайша, екі қарама - қарсы ағын: i _сед ағын седиментациясы және i _диф диффузия седиментациясы пайда болады.

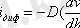, мұнда

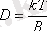
Бәсекелестік нәтижесінде бұл ағындардың үш нұсқасы пайда болуы мүмкін:

, демек

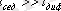
Теңсіздік орындалу үшін, Т және 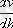мәндері аз болуы керек, ал ( ρ - ρ _о ) және v - үлкен болуы керек. Шынайы шарттарда бұл көрсеткіштерді өзгерту оңай емес, ал дисперсті жүйедегі бөлшектердің радиусы кең интервалда өзгереді: 10 ^-7 - дан 10 ^-2 см - ге дейін және осы бөлшектің радиусы анықтаушы болып табылады.

Егер r 10 ^-3 см болса, онда берілген теңсіздік орындалатыны дәлелденген. Бұл жағдайда диффузияны ескермеуге болады, бұл кезде жылдам седиментация жүреді - бұл жүйе седиментациялы тұрақсыз болады.

, демек ,
демек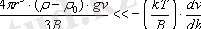

Бұл шарт егер Т және 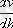үлкен, ал ( ρ - ρ _о ) және v - аз болғанда орындалуы мүмкін.

Бірақ бұл жерде шешуші рөлді бөлшектің радиусы атқарады. Ол r 10 ^-5 см теңсіздігі жүзеге асқанда орындалмақ.

Мұндай жағдайда седиментацияны ескермейтін болсақ, диффузия бөлшектердің барлық ыдыс көлеміне біркелкі таралуына әкеледі. Дисперсті жүйе седиментациялы тұрақты келеді.

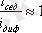, т. е. ,
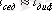демек

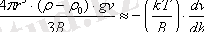
Жүйеде седиментациялы - диффузиялық тепе - теңдік орын алады. Мына теңдеуді ауыспалыға бөліп, интегралдасақ:

;
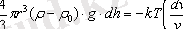
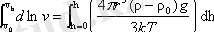қолданатын болсақ, ,
,
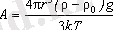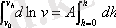мүндағы v _o - бөлшектің ыдыс түбіндегі концентрациясы; v _h - бөлшектің h биіктіктегі концентрациясы.
Осыдан
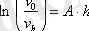
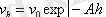
- Лаплас - Переннің гипсометрлік заңы шығады [3] . Бұл жағдайда жүйе седиментациялы - тұрақты болып табылады, дегенмен ондағы бөлшектерді анықтау теңсіздік емес, тепе - теңдік күйде болады. Бұл таралу 10 ^-5 < r < 10 ^-3 см байқалады.

Егер седиментацияны диффузияны есепке алып немесе есепке алмаған жағдайда салыстыратын болсақ, онда олардың кинетикалық тұрақтылығының түрлі фактторларға тәуелді екенін көрсетеді. Бұл факторлар кинетикалық седиментациялы тұрақтылықты (КСТ) және термодинамикалық тепе - теңдікті бір - бірінен ажыратуға мүмкіндік береді.

Седиментацияға кері константа КСТ өлшемі болып табылады.

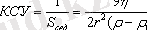
Осы тұрақтылық гидродинамикалық факторлармен қамтамасыз етіледі: ортаның тығыздығы мен тұтқырлығына, бөлшектің тығыздығы мен өлшеміне тәуелді келеді. КСТ кері сведбергте өлшенеді: кері. св. = 10 ¹³ с ^{- 1} .
ТСТ диффузияның статистикалық заңдарымен диффузиялы - седиментациялық тепе - теңдікке сәйкес шартталған. ТСТ өлшемі ретінде гипсометрлік биіктік алынады. Тұтқырлық ТСТ - ға әсер етпейді, ал Т ұлғаюы оның тұрақтылығының жоғарылауына мүмкіндік береді, демек, жылулық қозғалыс та жоғарылайды. КСТ ортаның тұтқырлығының азаюы нәтижесінде Т азаяды. Демек, дисперсті жүйелердің седиментациялық тұрақтылығы, басты негізде дисперсті фазадағы бөлшектердің өлшемі арқылы анықталады:

Лиофобты зольдер (10 ^{- 7} - 10 ^{- 5} см) - жүйеде көлемі бойынша бөлшектердің біркелкі таралуын қамтамасыз ететін седиментациялы тұрақты жүйелер;

Микрогетерогенді жүйелер (10 ^{- 5} 10 ^{- 3} см) - жүйе көлемі бойынша бөлшектердің гипсометрлік таралуын сипаттайтын седиментациялы - диффузиялық тепе - теңдік;

Ірідисперсті (10 ^{- 3} см көп) - жылдам седиментациялау өтетін, седиментациялы тұрақсыз жүйелер.

Тепе - теңдік жағдайдағы бөлшектердің биіктік бойынша таралуына Ла - Пласстың барометрлік формуласы қолданылады [4] :

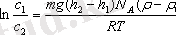
мұндағы m - бөлшек массасы;
h ₁ , h ₂ - биіктік деңгейлері;
с ₁ , с ₂ - h ₁ және h ₂ дейгейлеріне сәйкес концентрациялары;
ρ - бөлшектің тығыздығы;
ρ ₀ - орта тығыздығы.

Дисперсті жүйелердің агрегаттылығы.

Коллоидтық жүйелердің агрегаттық тұрақтылығы келесі факторлармен анықталады:

Термодинамикалық (электростатикалық, адсорбциялық - сольваттық және энтропиялық)
Кинетикалық - 1. Құрылымды - механикалық 2. Гидродинамикалық

Дисперсті жүйелердің агрегаттық тұрақтылығын төменгі факторларға Ван - дер - Вальстік тартылу күштері, бөлшектердің заряды және потенциялдық әсер ететін электролиттердің болуы жатады. Осы агрегаттық тұрақтылықты қарастыратын теориялардың бірі - ДЛФО теориясы.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.