Санау жүйесі

1. Санау жүйесі

Санау( Счисление; notation) - сандарды бейнелеу және өрнектеутеу тәсілі.

Санау жүйесі (Система счисление; notation system) дегеніміз - сандарды цифрлық таңбалар арқылы жазу мен оқу тәсілдерінің жиынтығы немесе санау жүйесі деп сандардың аталуы және жазылу әдісін айтады. Барлық санау жүйелері позициялық және позициялық емес болып екіге бөлінеді.

Позициялық санау жүйесінде цифрдың мәні оның сан жазылуындағы орнына(позициясына) байланысты болады(мыс., екілік, сегіздік, ондық және он алтылық санау жүйелері) . Мысалы, 999 санын алсақ, 9 санының мәні тұрған орнына байланысты өзгереді(жүздік, ондық, бірлік) .

Тұрмыста ондық санау жүйесі кеңінен қолданылады. Есептеуіш техникада позициялы санау жүйелері пайдаланылады: екілік - негізгі санау жүйесі ретінде, ал ондық, он алтылық - қосымша санау жүйесі ретінде.

Рим санау жүйесі-позициялық емес, мұнда санның мәні оның тұрған орнына тәуелді емес, яғни Х саны мына XXI санында орнына байланыссыз “он” болады.

Рим сандары латын әріптерімен жазылады.

I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000,

Мысалы: VI=5+1=6; XXI=10+10+1=21; IV=5-1=4.

Санау жүйесінің негізгі деп позициялық санау жүйесінде қолданылатын әр түрлі цифрдың саны. Ондық санау жүйесінде он цифр қолданылады: 0, 1, 2 . . . , 9; екілік санау жүйесінде - екі: 0 және 1; сегіздік санау жүйесінде - сегіз; 0, 1, 2, . . . , 7. Q негізгі болып келген санау жүйесінде 0 - ден (Q-1) -1 дейінгі цифрлар қолданылады да, олар осы жүйенің базистік цифрлары деп аталынады.

Q негізгі болып келген позициялық санау жүйесінде жалпы түрде кез келген x санын көпмүшелік түрінде өрнектеуге болады:

x = $a_{n}Q^{n} + a_{n - 1}Q^{n - 1} +$ … $+ a_{1}Q^{1} + a_{0}Q^{0}$ + $a_{- 1}Q^{- 1} + a_{- 2}Q^{- 2} +$ …+ $a_{- n}Q^{- n}$ (1)

бүтін бөлігі бөлшек бөлігі

Мұндағы, $a_{1}$ коэффициенті ретінде қолданылған осы санау жүйесіндегі цифрдың кез келгені бола алады.

Q негізі болып келген позициялық санау жүйесінде x санының жазылуы үлгісі:

x =( $a_{n}a_{n - 1}$ … $a_{1}a_{0}, a_{- 1}a_{- 2}$ … $a_{- n}) _{Q}$ немесе x = $a_{n}a_{n - 1}$ . . . $a_{1}a_{0}a_{- 1}a_{- 2}$ . . . $a_{- n}$ (2)

Бүтін бөлігі бөлшек бөлігінен үтір(есептеу техникасында көбінесе нүкте қолданылады) арқылы ажыратылады.

Мысалы:

Дербес компьютер негізінен екілік, ондық, он алтылық санау жүйелерінде жұмыс істейді (әр жүйеге сәйкес базистік цифрлар 1. 1 - кестеде қоршалып көрсетілген) . Он алтылық санау жүйесіндегі A, B, C, D, E, F әріптері осы жүйенің сәйкес 10, 11, 12, 13, 14, 15 цифрларын анықтайтын символдар.

1. 2. Сандарды ондық жүйеден екілік жүйеге аудару

Сандарды ондық жүйеден екілік жүйеге аудару, санның бүтін және бөлшек бөліктері үшін келесі алгоритм бойынша жеке жүргізіледі

а) бүтін ондық санды екіге бөлеміз, шыққан бөліндіні (бірден өзгеше болса) тағы екіге бөлеміз, одан шыққан санды да, бөлінді бірге тең болғанша, біртіндеп екіге бөле береміз. Ең соңғы бөліндіден басталып жазылатын қалдық сандар тізбегі, ізделініп отырған екілік жүйедегі санды береді (1. 1-сурет) .

218 ₁₀ =11011010 ₂ ;

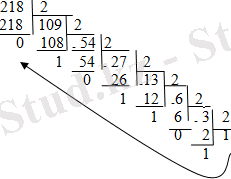
1. - сурет Санды ондық жүйеден екілік жүйеге аудару.

ә) ондық бөлшек 2 негізіне біртіндеп көбейтіліп, шыққан көбейтіндінің бүтін бөлігі нәтижеге жазылып, келесі көбейтіндіге қатыспайды. Көбейту операциясының саны қажет дәлдікке байланысты мысалы, мысалы, 0. 59375 ₁₀ =0. 10011 ₂

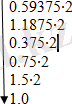
1. 3. Сандарды екілік жүйеден ондық жүйеге ауыстыру

Сандарды екілік жүйеден ондық жүйеге аудару жоғарыда көрсетілген (1), (2) өрнектер бойынша жүзеге асады, мысалы, бүтін 11011010 ₂ екілік саны үшін Q=2, n=7; бөлшек 0. 10011 ₂ екілік саны үшін Q=2, m=5, ендеше:

11011010 ₂ = 1∙2 ⁷ +1∙2 ⁶ +0∙2 ⁵ +1∙2 ⁴ +1∙2 ³ +0∙2 ² +1∙2 ¹ +0∙2 ⁰ =128+64+16+8+2=218 ₁₀

0. 10011 ₂ =1∙2 ^-1 +0∙2 ^-2 +0∙2 ^-3 +1∙2 ^-4 +1∙2 ^-5 =0. 5+0. 0625+0. 03125=0. 59375 ₁₀

1. 4. Компьютерде теріс сандардың ұсынылуы

ЭЕМ жадында екілік сандар 8 ұяшықтардан құрылған (сегіз разрядты) регистрлерде сақталынады. Ал регистердің толмай қалған ұяшықтарында (разрядтың үлкенінде) нөлдер жазылады.

Екілік сану жүйесінің оңдық жүйеден айырмашылығы, санның таңбасын білдіретін: (+) оң немесе (-) теріс - арнайы символдарының болмауында. Сондықтан, екілік теріс санды ЭЕМ жадында көрсету (кодтау) үшін, келесі екі форма қолданылады.

Таңбалы мән формасы (тура код) - разрядтың үлкені (сол жақ) таңбалы есептелініп, тек санның таңбасы жайында информация береді:

1 - санның теріс екенін;

0 - санның оң екенін білдіреді.

Қалған разрядтар (орын) санның абсолюттік мәніне беріледі.

Мысалы, 6 ₁₀ = 0110 ₂ болса, онда - 6 ₁₀ = 1000 0110 ₂ немесе - 6 ₁₀ = 1’000 0110 ₂ (мұнда, < ’ > - белгісін қою арқылы таңбалы разряды ажыратылып көрсетілген) .

Кері қосымша код формасына , келесі аудару алгоритмі арқылы жүргізіледі:

1) санның таңбалы разрядтан басқа барлық разрядтарын терістету;

2) шыққан кодқа бірді қосу;

3) таңбалы разрядтағы бірді қалпына келтіру.

Санды түрлендіру

-6 ₁₀ = 1’000 0110 → 1’111 1001+1 → 1’111 1010→ 1010.

Әдетте оңдық теріс сан компьютерге енгенде автоматты түрде кері кодқа немесе қосымша кодқа түрленіп, машинаның жадында осындай түрде сақталып және басқа да операцияларға осы күйінде қатысады. Осы санды машинадан кері шығарғанда, оңдық теріс санға кері түрлендіру жүргізіледі.

Сонымен -логикалық құрылғысының конструкциясын жеңілдету мақсатында, әр түрлі арифметикалық операцияларды қосу операциясымен ауыстырады.

Қосымша кодтың негізгі қасиеттері:

1. Оң санның қосымша коды - санның өзі.

2. Аудару алгоритмі бойынша қосымша кодты түрлендіру, санды алғашқы таңбалы формасына әкеледі.

1. 5. Компьютерде бүтін сандардың ұсынылуы

Компьютерде бүтін сандар таңбасыз немесе таңбалы түрде көрсетілуі мүмкін.

Таңбасыз бүтін сандар әдетте бір байттық немесе екі байттық жадта орналасады. Бір байттық форматта - ₂ -ден ₂ -ге дейін мәндерді, ал екі байттық форматта - ₂ -ден ₂ - ге дейін мәндерді қабылдайды.

Таңбасыз бүтін сандардың мәндерінің диапазоны

Мысалы:

a) 72 ₁₀ = 1001000 ₂ саны бір байттық форматта:

Разрядтың нөмірі

Санның биті

б) осы сан екі байттық форматта:

Разрядтың нөмірі

Санның биті

в) 2 ¹⁶ - 1 = 65535

Разрядтың нөмірі 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Санның беті

Таңбалы бүтін сандар әдетте компьютердің жадында бір, екі немесе төрт байттық орын алады. Сол жақ (үлкен) разряд санның таңбасы жайында информация береді.

Таңбалы бүтін сандардың мәндерінің диапазоны

Байт Диапазоны

Реті арқылы жазылу Кәдімгі жазылу

1 -2 ⁷ _2 ⁷ -1 -128_127

2 -2 ¹⁵ __2 ¹⁵ -1 -32768_32767

3 -2 _2 -1 -2147483645_2147483647

Он бүтін сан тура, кері және қосымша кодта бірдей бейнеленеді: екілік кодта, таңбалы разрядында 0- цифрасымен,

Мысалы:

Бір байттық форматта

1 ₁₀ -1 ₂ саны: 127 ₁₀ - ₂ саны:

Теріс бүтін сан тура, кері және қосымша кодта әртүрлі бейнеленеді.

1. Тура код. Таңбалы разрядында 1 - цифрасы орналасады, ал қалған разрядтарында абсолют шамадағы санның екілік коды.

Мысалы.

- 1 санының тура коды: -127 санының тура коды:

2. Кері код. Абсолют шамадағы санның екілік кодын таңба разрядымен қоса тегістеу: нөлдерді - бірлерге, бірлерді - нөлдерге ауыстыру.

Мысалы:

Санының кері кодын есептеу:

3. Қосымша код. Санының кері кодының кіші разрядына бірді қосқаннан шығады.

Мысалы:

-1 санының қосымша коды: -127 санының қосымша коды:

1. 2 кестеде -8_8 аралдығындағы ондық сандарды тура, кері және қосымша кодтары берілген.

1. 2 - кесте

1. 6. Ескілік жүйеде арифметикалық амалдардың

орындалу ережелері

Екілік сандармен арифметикалық амалдардың ( қосу, азайту және көбейту ) орындалу ережелері келесі кестеле корсетілген.

Барлық позициялық санау жүйесінде арифметика ережелері осы тәріздес. Цифрларды қосқанда сәйкес разрядтары бойынша қосылады да, толып кеткен жағдайда сол жаққа көшіріледі. Қәзіргі заманда компьютерлерде барлық арифметикалы амалдырды орындайтын тек қана бір аппараттық қосындылауыш (сумматор) болғандықтан, азайту амалы - теріс санды қосуға әкеледі.

17 - 9 = 17 + (-9)

Екілік жүйеде азайту ережесі. Қосымша кодты қосу арқылы азайту амалының алгоритмі:

1. теріс санды таңбалы формасынан (тура кодынан) қосымша

кодқа түрлендіру;

2) ең үлкен разрядтан өтетін бірге ғана мән бермей, барлық

разрядтарына ( таңбалы разрядтан да есептеп ) екілік қосу амалын

орындау;

3) қосындысының таңбалы разрядының бірге тең болған жағ-

дайы, теріс санның қосымша қол формасында шыққанын білді-

реді. Қосымша кодтың екінші қасиетін қолданып, наәтижені таң-

балы формаға келтірі керек.

Мысалы :

15 - 18 = 25 + (-18)

15 ₁₀ = ₂

18 ₁₀ = 10010 ₂

1) -12 ₁₀ = 1´0010010→1´1101101 + 1→1´1101110→11101110

2)

11101110

01

3) 01→1´01→1´10 + 1→111 = -3 ₁₀

Көбейту. Егер көрсетілген амалдармен қатар ығысу амалын

орындасақ, онда бірнеше рет қайта қосу амалына келтірілетін

көбейту амалын, қосындылауыш арқылы орындауға болады.

Мысалы :

14 ₁₀ · 11 ₁₀ = 154 ₁₀ = 10011010 ₂ = 1 · 2 ⁷ + 1 · 2 ⁴ + 1 · 2 ³ + 1 · 2 ¹ =154 ₁₀

14 ₁₀ = 1110 ₂ ; 11 ₁₀ = 1011 ₂ ;

1110

1011

1110

1110

1110

00010011010

Бөлу. Бөлу амалын орындаған кезде, бірнеше рет азайту амалы жүргізіледі. Сондықтан алдын-ала бөлгіштің қосымша кодын табу керек. Бөлу азайту мен ығысуды қайталау арқылы орындалады. Мысалы үшін 154 санын 14-ке бөлейік, немескс екілік жүйеде сәйкес 10011010 ₂ санын 1110 ₂ -ке бөлейік. 1110 санының қосымша коды 0010. Бөлу ережесі бойынща әрбір аралық бөлінгіш бөлгіштен үлкен болуы керек. Бірінші бөлінгіш ретінде

10011санын таңдаймыз, яғни алғашқы бес разрядын және бөлінгішті сол жағынан үш нөлмен 8 разрядқа дейін толтырамыз. Оған бөлгіщтің қосымша кодын қосамыз және нәтижеге бірді жазамыз. Егер келесі аралық бөлінгіш, кезекті цифрді түсіргеннен кейін бөлгіштен кіші болса, онда нәтижеге нөл жазылып, аралық бөлінгішке бастапқы бөлінгіштен тағы да бір цифр түсіріледі.

1. Санды атау және жазу әдістерінің жиынтығы қалай аталады?

А) санау жүйесі;

В) сандық заңдылық;

C) жетекшілік;

D) кодтау жүйесі;

Е) пайдаланушының жетекшілігі.

2. Екілік жүйесі мына цифрларды қолданады:

A) 4 және 3;

B) 1 және 0;

С) 1 және 2;

D) 0 және 2;

E) 8 және 5.

3. Информацияны берудің бір түрінен келесі түріне өту процесі қалай аталады?

A) дефрагменттеу;

B) форматтау;

C) кодтау;

D) сканерлеу;

E) аудару.

4. Түрлендіру кезіндегі алфавиттің әріппетірінің сәйкес болуын сипаттайтын ережелер:

A) декодтаушы;

B) хабарламалар;

C) кодтаушы;

D) кодтар;

E) қайта кодтаушы.

5. 729, 854 санның ондық жүйеде жазылуы:

A) 7*10 ² +2*10 ^-1 +9*10 ⁰ +8*10 ^-1 +5*10 ^-2 +4*10 ^-3 ;

B) 7*10 ³ +2*10 ² +9*10 ¹ + 8*10 ^-0 +5*10 ^-1 +4*10 ^-2 ;

C) 7*10 ³ +2*10 ² +9*10 ¹ +8*10 ^-1 +5*10 ^-2 +4*10 ^-3 ;

D) 7*10 ² +2*10 ¹ +9*10 ⁰ +8*10 ^-0 +5*10 ^-1 +4*10 ^-2 ;

E) 7*10 ³ +2*10 ¹ +9*10 ⁰ +8*10 ^-0 +5*10 ^-1 +4*10 ^-2 .

6. Позициялық санау жүйесінің негізі:

A) сандарды жазғанда қолданылатын бір-бірінен ерекше белгілер саны;

B) жүйедегі сандарды аудару формуласындағы логарифм негізі;

C) жүйеде есептеудің ережелер саны;

D) санның бүтін бөлігі;

E) санның бөлшек бөлігі.

7. 1 байт =

A) 1024 бит ;

B) 8 бит;

C) 8 байт;

D) 1 Мбайт;

E) 1 Кбайт.

... жалғасы

Санау жүйесі туралы түсінік

Санау жүйесі туралы ақпарат

Санау жүйелері тақырыбын оқыту әдістемесі

Сандарды бір санау жүйесінен екінші санау жүйесіне ауыстыру

Санау жүйесi. Санау жүйесінің түрлері. Бір санау жүйесінен екіншісіне өту жолы.

Бүтін ондық сандарды екілік санау жүйесіне ауыстыру

Сандар туралы мәлімет және санау жүйесінің тарихы

Римдік санау жүйесі

Санау жүйелері. Буль алгебрасы

Санау жүйелері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс