Ықтималдықтар теориясының қоғамдағы орны: тарихы, негіздері және қолданбалы маңызы


Ықтималдықтар теориясының қоғамдағы
орны
Адам ойы мен қиялы өте шексіз. Жылдарға, ғасырларға кейіндеп
те, ілгерілеп те алға оза алады. Саналы адам көрсем, білсем, үйренсем
деп тұрады. Көрген, білгенінен ой түйіндейді, қорытынды шығарады.
Математика, физикада қарастырылатын есептер көбінесе бір мәнді
анықталады. Мысалы: қолымызбен тасты лақтырсақ, онда тастың
орнын кез-келген уақыт кезеңінде анықтай аламыз. Бірақ ғылымның
әр саласында, техникада, шаруашылық саласында қолданылатын
көптеген есептер бір мәнді анықталмайды. Мысалы: тиынды
лақтырып, оның қай жағымен түсетінін нақты айтуға болмайды.
Мұндай жағдайда осы сияқты есептерді шешуде белгілі бір нақты
шешім айтуға болмайтын тәрізді көрінеді. Алайда бұл тәжірибеде
керісінше. Ойын практикасы көрсеткендей тиынды неғұрлым көбі-
рек лақтырсақ, солғұрлым әрекеттің жартысында елтаңба жағы
түссе, енді жартысында цифр жағы түсетіні байқалды. Бұл кез-
соқ оқиға. Белгілі бір заңдылыққа байланысты. Міне осындай заң-
дылықтарды ықтималдық теориясы қарастырады. Ең қарапайым
мысал ретінде тиын лақтыруды алдық. Бірақ ықтималдықтар теория-
сында бұдан да күрделірек есептер қарастырылады. Шаруашылықтағы
маңызды мәселенің бірі аудан мен облысты байланыстыратын теле-
фон жүйесін орнату. Бұл да таза ықтималдық есеп. Мысалы:мұнда
орталықтан ауданға телефон жүйесін тарту үшін қанша сым қажеттігі
белгілі болу керек. Өмірде мұндай мәселелер көптеп кездеседі.
Осындай мәселелер өндіріс саласын жоспарлауда, зерттеулер
жүргізуде қолданылады. Мысалы:сынып арасында өткізілетін
жарыстардың нәтижесі дәлірек болу үшін нәтижелер ондық үлеспен,
жүздік үлеспен есептелінеді. Сонда әр сыныптың нәтижесі дәлірек
болу үшін қанша таңбаға дейін алу керек деген сұрақ туындайды.
Неғұрлым сынақ көп жасалынса, солғұрым нәтиже дәл болаты-
ны белгілі. Ал ол үлкен шығынға әкеледі. Міне, осы арада ықтимал-
дықтар теориясы көмекке келеді. Адамның күнделікті өмірі, дүниені
танып-білу барысы кездейсоқ оқиғаға толы. Бұл кездейсоқтықтар
өмірдің даму заңдылығына кедергі келтірмейді, керісінше,
кездейсоқтық пен заңдылық біріне-бірі әсер етіп, өмірдің дамуына
себепші болады.
Кездейсоқтық? Оны оқып үйрену не үшін қажет?-деп сұрайтын
боларсыздар? Шын мәнінде, адамдар, ерте кездің өзінде-ақ оқиға
өмірдегі бір ерекшелік емес, қағида екендігін байқаған. Міне сон-
дықтан да кездейсоқ құбылыстар туралы ғылым пайда болды.
Кездейсоқтық заңдарын білу қажет. Осыған байланысты мынадай
мысал қарастырайық. Барлық ірі елді мекендерде «медициналық
жедел жәрдем» станциялары бар. Кенеттен және қатты ауырып қалған
адамдарға жедел жәрдем көрсету қажет болатын уақытты алдын
ала болжап айту мүмкін емес. Берілген уақыт аралығында мұндай
ауруларға шақырулардың көптігі қандай болады?Дәрігер мен «жедел
жәрдем» машинасына аурудың қасында қанша уақыт кідіруіне
тура келеді? Бір жағынан, аурулар жәрдемді өте ұзақ күтпеуі,
екінші жағынан дәрігерлер құрамын өте тиімсіз пайдалану байқалмас
үшін, кезекшілік кезінде қанша дәрігер және машина болуы қажет?
Біз шақырту уақыттары, дәрігердің аурудың қасында болу ұзақтығы,
машинаның «Жедел жәрдем»пунктінен, ауру тұратын үйге дейін
жолда болу ұзақтығы . . . кездейсоқ болып табылатын әдеттегі жағдай-
мен кездесіп отырмыз. Демек, амал біреу ғана:бұл жәрдем шынында
да шұғыл болу үшін, барлық кездейсоқтықты ескере білу керек. Міне,
тіпті осындай күнделікті мәселе де кездейсоқтықты білуді талап ете-
ді. Сондықтан да оны оқып үйрену қажет. Осындай практикалық
жұмыстарда есептеу әдістерін қолдана білуге үйрену, жалпы
математикалық білім деңгейімді жетілдіру, пән бойынша жүйелі
білімімді қалыптастыру, өмірде кездесетін оқиғаларды сараптай білу
менің міндетім болып отыр.
Математика-нақты ғылым, бір қарағанда кездейсоқтыққа ешқандай
қатысы жоқ. Бірақ, осы кездейсоқтықтың сандық сипаттамасын,
ықтималдық ұғымын берген басқа емес, осы математика.
Ықтималдықтар теориясы өмірдегі кездейсоқтықтарды зерттеп,
олардың заңдылықтарын ашады.
I тарау 1. 1. Ықтималдықтар теориясының тарихына шолу
Ықтималдықтар теориясы өз бастауын XVII ғасырдан алады. Алдымен
азартты ойындар пайда болды. Араб тілінде «азар» деген сөз «қиын»
деген мағына береді. Арабтар « азар » деп лақтырылған ойын сүйегі-
нің екеуінде де 6 ұпайдан түсүін айтады екен. Куб түріндегі ойын
құралы ол кезде піл сүйегінен жасалатын болғандықтан « ойын
сүйегі » деген атау сол заманнан қалыптасып қалған. Ықтималдықтар
теориясы жөніндегі алғашқы жұмыстар XVII ғасырда басталды.
Еуропа елдерінде адамды құнықтыратын әр түрлі ойындардың кең
таралуына байланысты әр ойыншы өзінің жеңілмеу ықтималдықды-
ғын алдын ала анықтауға тырысты. Сол кездегі математиктер де бұл
мәселеге назар аудардып, бірнеше рет қайталанатын кездейсоқ
оқиғалар туралы заңдылықтар ашуға талпынды. Бұл мәселеге алғашқы
болып еңбектерін ұсынған:француз оқымыстысы Блез Паскаль, Пьер
Ферма, голландиялық Христиан Гюйгенс, швецариялық математик
Яков Бернулли болды. Француздың атақты математиктері Пьер
Ферма мен Блез Паскальдың азартты ойындар жөніндегі зерттеулері
ықтималдықтар теориясының негізін қалады. Кейіннен сақтандыру
жұмыстарында және демография саласында ықтималдықтар
теориясы өз қолданысын тапты.
Жаратылыстану ғылымдары мен техниканың дамуы ықтималдық-
тар теориясына жаңа мәселелер қойды. Ықтималдықтар теориясының
дамуын Бернулли, Муавр, Гаусс, Лаплас, Пуассон еңбектері көп әсер
етті. XIX ғасырдың екінші жартысыннан бастап бұл саланың дамуына зор
әсер еткен В. Я. Буняковский бастаған математиктер
мектебі:П. Л. Чебышев, А. А. Марков, С. Н. Бернштейн, А. Н. Колмогоров
секілді орыс ғалымдары үлкен үлес қосты.
XVIII ғасыр аяғы мен XIX ғасыр басында ағылшын оқымыс-
тысы А. Муавр, орыс оқымыстыларыЛ. Эйлер, Н. Бернулли, Д. Бернулли,
француз П. Лаплас, С. Пуассон, неміс К. Гаусс геодезия мен астрано-
мияның өркендеуіне қатысты өлшеу қателіктерін бағалау, ату
теориясындағы снарядтардың жағдайларын анықтау үшін ықтимал-
дықтар теориясының рөлін көрсету мақсатында ғылыми жұмыстар
жүргізді. XIX ғасыр ортасында Ф. Гальтон, Л. Больцман, А. Кетле, А. М. Ляпунов, П. Л. Чебышев,
А. К. Калмогоров сияқты оқымыстылар жиындар теориясы, шақты айнымалылы функциялар теориясы, функционалдық анализ сияқты жоғары математикалық жаңа табыстарына сүйенетін ықтималдықтар теориясының өркендеуіне негіз салды.
Ықтималдықтар теориясының дамуына байланысты оның адамзат өмірінде қолдану мүмкіндігі артты. Жалпы алғанда ықтималдықтар теориясының әдісі ғылымның барлық саласына өз үлесін қосады. Ал математика ғылымында алатын орны ерекше.
Зерттеу бөлімі
Оқиғалар ұғымы ықтималдықтар теориясының негізгі ұғымдарының бірі болып табылады. Белгілі бір шарттар орындалғанда пайда болатын құбылысты оқиға дейміз. Осы шарттарды іске асыруды сынақ, тәжірибе не бақылау жүргізу дейміз. Мысалы, лақтырылған асықтың түсуін бақылайық. Ол бүк, шік, алшы, тәйкі деген жақтарымен түсе алады. Алдын-ала асықтың қай жағы түсетіні белгісіз болғандықтан оқиға кездейсоқ оқиға деп аталады. Тағы бір мысал, біз үлкендіктері бірдей үш параққа А, В, С әріптерін жазып, араластырып, қатар қойғанда, әр түрлі реттікпен орналаса алады:«АВС», «АСВ», «ВАС», «ВСА», «СВА», «САВ». Тәжірибе нәтижесінде пайда болған немесе пайда болмаған оқиғаны сонымен қатар ол оқиғалардың ықтималдықтар теориясының пәнін анықтайды. Оқиғаларды латын әріптері А, В, С және т. с. с арқылы белгілейді. Оқиғалар бірнеше түрге бөлінеді: мүмкін болатын оқиға, мүмкін емес теңмүмкіндікті, үйлесімсіз, үйлесімді оқиғалар. Сынақ нәтижесінде міндетті түрде болатын оқиға мүмкін болатын оқиға деп, ал сынақ нәтижесінде ешқашан орындалмайтын оқиға мүмкін емес оқиға деп аталады. Жәшіктен қосалқы бөлшектер ішінде стандартқа сай бөлшектер алу тәжірибесі. Осы жәшіктен стандартқа сай бөлшекті алу міндетті түрде орындалады. Ал ешқашан осы стандартқа сай емес бөлшекті алу орындалмайды. Яғни стандартқа сай бөлшектер салынған жәшіктен стандартқа сай бөлшекткер алу оқиғасы мүмкін болатын оқиға. Ал осы жәшіктен стандартқа сай емес бөлшекті алу оқиғасы мүмкін емес оқиға болып табылады. Мүмкін болатын оқиғаны U әрпімен белгілейді, ал мүмкін емес оқиғаны V әрпімен белгілейді.
Бес ақ және бес қара қарындаш бар қораптан «ақ қарындаш алу» және «қара қарындаш алу» оқиғаларының мүмкіндіктері бірдей. Өйткені, ақ қарындаш саны және қара қарындаш саны бірдей. Ал екі қара және жеті ақ шар алу оқиғасының теңмүмкіндікті оқиға бола алмайды. Өйткені шарлар саны әр түрлі.
Теңмүмкіндікті оқиға деп-тәжірибедегі оқиғалардың пайда болу мүмкіндігі бірдей оқиғаларды айтамыз.
Ойын сүйегін бір рет лақтырғанда, тек біреуі ғана орындалады. Нәтижесінде пайда болатын оқиға қалғандарын болдырмайды. Тағы бір мысал, оқушы бір емтихан тапсырып, бір мезгілде «өте жақсы» деген және «жақсы» деген баға ала алмайды. Демек, мұндағы«өте жақсы» және «жақсы» деген бағалар алу оқиғалары бір-біріне үйлесімсіз оқиғалар. Кері жағдайда ол екі оқиға үйлесімді оқиғалар деп аталады. Мысалы, бір оқушы екі емтихан тапсырып, бірінен «өте жақсы» деген, ал екіншісінен «жақсы» деген баға алуы үйлесімді оқиғалар болып табылады
Үйлесімсіз оқиға дегеніміз-тәжірибедегі оқиғалардың бірінің пайда болуы басқасын болдырмайтын оқиға. . Егер екі үйлесімді оқиғаның біреуі міндетті түрде жүзеге асса, онда екіншісі біріншісі оқиғаға қарама-қарсы оқиға деп аталады.
Ықтималдықтың классикалық анықтамасы.
Ықтималдықтар теориясының негізгі ұғымдарының бірі оқиға ықтималдығы болып табылады. Ықтималдықтар ұғымын анықтаудың бірнеше түрі бар: классикалық, статистикалық және т. б.
Өмірде «ықтимал» деген сөз көп кездеседі. Егер күн бұлттанып тұрса, жаңбыр жауу ықтимал дейді. Ықтимал сөзінің синонимі «мүмкін» деген сөз.
Әр жағдайда адам ойлап, қандай да бір оқиғаның басқа бір оқиғаға қарағанда пайда болу ықтималдығы көбірек, не азырақ екенін аңғарады. Оқиғаның табиғи пайда болу дәрежесінің сандық өлшемі оқиға ықтималдығы деп аталады.
Ойын сүйегін бір рет лақтырғанда, оның 1, 2, 3, 4, 5, 6 нөмірлі жақтарының кез-келгені түсе алады. Ойын сүйегінің жұп нөмірлі жақтарының түсу ықтималдығын табайық.
Тәжірибедегі оқиғаның пайда болуына қолайлы оқиғалар санының мүмкін болатын оқиғалар санына қатынасын оқиғаның ықтималдығы дейміз.
А оқиғасының пайда болу ықтималдығы:
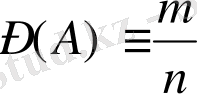
мұндағы m-А оқиғасының пайда болуына қолайлы оқиғалар саны, n- берілген тәжірибедегі мүмкін болатын оқиғалар саны
Бұл анықтама оқиға ықтималдығының классикалық анықтамасы деп аталады.
Пайда болатын оқиғалар теңмүмкіндікті және үйлесімсіз. Бізге оқиғаның пайда болуына қолайлы оқиғалар саны m-үшеу.
Олар:2, 4, 6. Тәжірибедегі мүмкін болатын оқиғалар саны n- алтау.
Сонымен формулаға сүйене отырып:
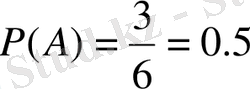 жұп сандардың түсуінің ықтималдығы
0, 5
тең болды.
жұп сандардың түсуінің ықтималдығы
0, 5
тең болды.
Ықтималдықтың классикалық анықтамасынан оқиға ықтималдығының мындай қасиеттері туындайды:
1-қасиет. Мүмкін болатын оқиғаның ықтималдығы бірге тең:
P(U) =1
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz