Нақты сандарды рационал сандармен және үздіксіз бөлшектермен жуықтаудың теориясы


Мазмұны
Кіріспе . . .
І-Тарау . Нақты санды жуықтаудың кейбір қарапайым әдістері .
§1. 1. Дирихле принципі . . .
§1. 2. Фарей қатары . . .
II-ТАРАУ. Нақты сандарды үздіксіз бөлшектермен жуықтау
§2. 1. Үздіксіз бөлшектердің лайықты бөлшектері және олардың қасиеттері . . .
§2. 2. Ең жақсы жуықтау . . .
Қорытынды . . .
Пайдаланған әдебиеттер тізімі . . .
Кіріспе
Курстық жұмыста нақты сандарды рационал сандармен жуықтау теориясы мен олардың практикада қолданылуы қарастырылады. Кез келген нақты санды алдын ала берілген дәлдікпен рационал бөлшектер арқылы өрнектеуге және де әрбір нақты санды бір ғана үздіксіз бөлшек түрінде көрсетуге мүмкіндік тудырады. Бұл жағынан алғанда үздіксіз бөлшектердің маңызы ондық бөлшектерден кем түспейді. Сонымен қатар үздіксіз бөлшектердің лайықты бөлшектері және негізгі қасиеттері қамтылады. Үздіксіз бөлшектердің таза практикалық қолданылуымен қатар теориялық маңызы да зор. Олардың әдістері негізінен алғанда сандар теориясында, алгебрада, ықтималдықтар теориясында, тіпті анализ бен механикада да қолданылады. Нақты сандарды рационал сандармен жуықтау сандар теориясы курсын оқу үшін аса қажетті болып табылады.
Курстық жұмыс кіріспеден, екі тараудан және қорытындыдан тұрады. Бірінші тарауда нақты сандарды жуықтаудың кейбір қарапайым әдістерінің қолданулары көрсетілген. Екінші тарауда нақты сандардың үздіксіз бөлшектермен жуықталуы, ақырлы және ақырсыз үздіксіз бөлшектер анықтамасы, жазылуы, мәндері және ең жақсы жуықтау әдістері сипатталған.
І-ТАРАУ.
НАҚТЫ САНДАРДЫ ЖУЫҚТАУДЫҢ КЕЙБІР
ҚАРАПАЙЫМ ӘДІСТЕРІ.
1. 1. Дирихле принципі
Айталық,
 саны
саны
 нақты сандар жиынынан алынған сан болсын. Белгілеп алынған α нақты саны үшін
нақты сандар жиынынан алынған сан болсын. Белгілеп алынған α нақты саны үшін
 рационал санын қарастырайық, мұндағы р
рационал санын қарастырайық, мұндағы р
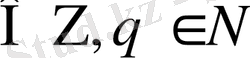 мына
мына
(1)
айырымының абсолют шамасын анықтау өте маңызды. Нақты сандар ішінде рационал сандар жиыны тығыз орналасқаны белгілі. Сондықтан (1) -нің шамасын кез келген алдын ала берілген аз оң нақты саннан кіші етіп алуға болады, мұндағы p, q сандарын қалауымызша таңдап алынған.
Көбіне (1) -ні бағалау үшін
рационал санның бөлімінен тәуелді функцияны алады, яғни
< φ(q) (2)
Бұл теңсіздіктің оң жағындағы функция α нақты санының
рационал санымен жуықталудың ретін көрсетеді.
Егер α санынан және φ(q) функциясынан тәуелді с>0 саны табылып, мына
<сφ(q) (3)
теңсіздігі үшін р
сандары шексіз көп орын алса, онда α нақты саны рационал санмен жуықталады деп айтады. Ал (3) -ші теңсіздіктің
шешулері ақырлы болса (

α), онда α санының ең жақсы рационал жуықтауы
бар деп айтамыз. Бұл жерде
>с ´ φ(q) теңсіздігі кез келген
үшін орындалатындай α санымен φ(q) функциясынан тәуелді с´ тұрақтысы табылады.
Көп жағдайларда φ(q) функциясы ретінде
φ(q) =
(4)
өрнегін алсақ, онда α санының жуықтауы µ ретті дәрежелік жуықтау деп аталады. Мұндағы µ және с сандарының әртүрлі мәндерінде (3) -нң ақырлы немесе ақырсыз шешулер саны болуы мүмкін.
Егер
, онда (1) айырымын анықтау оңай шешіледі.
болсын. Егер тек
болса, онда
(5)
Бұдан
(6)
теідеуінің кез келген
,
кезінде
шешімі болмайды.
Бір жағынан сандар теориясынан келесі екі айнымалылы анықталған теңдеуінің

х немесе у бүтін сандарында шексіз шешімдері бар болады. Сондықтан (5) теңсіздігіндегі теңдік белгісі
болғанда шексіз көп сандар үшін орындалады. . Осылайша (6) теңсіздігінің кез келген
кезінде
және
сандарында шексіз көп шешімі болады.
Әр түрлі нақты сандар үшін рационалды сандармен жуықтау реті әр түрлі болады. Әрі қарай
дегі барлық иррационалдық сандар µ = 2 жуықтау ретін береді, сонымен қатар олардың арасында жақсы жуықтау ретін беретін сандар бар болатынын көрсетеді.
Дирихле принципі қарапайым тұжырымға негізделген:
Егер
заттарды
жәшік бойынша таратсақ, онда
болғанда жәшіктердің ең болмағанда біреуіне екі зат түседі. Тұжырымның қарапайымдылығына қарамастан, бұл әдіс сандар теориясының әр түрлі бөлімдеріндегі көптеген қажетті теоремаларды дәлелдеуге мүмкіндік береді.
Дирихле теоремасы.
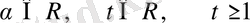 болсын. Онда келесі теңсіздік орындалатындай
болсын. Онда келесі теңсіздік орындалатындай
 (7)
(7)
 және
және
 бар болады.
бар болады.
Дәлелдеуі
:
Ең алдымен
 болсын дейік.
болсын дейік.
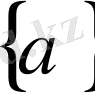 және
және
 түрінде
түрінде
 санының сәйкес бөлшек және бүтін бөліктері белгіленсін.
санының сәйкес бөлшек және бүтін бөліктері белгіленсін.
 (8)
(8)
сандарының
 сандарын қарастырайық. Бөлшек үлесінің қасиеті бойынша
сандарын қарастырайық. Бөлшек үлесінің қасиеті бойынша
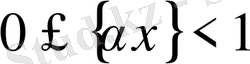 (9)
(9)
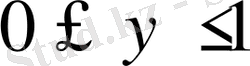 жарты интервалында
жарты интервалында
 ұзындығымен бірдей
ұзындығымен бірдей
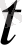 кіші интервалдарға бөлейік.
кіші интервалдарға бөлейік.
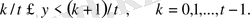 (10)
(10)
(9) теңсіздігіне сәйкес (8) теңсіздіктің сандарының әрбіреуі (10) кіші интервалының біріне жатады. Бірақ (8) сандары тура
 , ал (10) кіші интервалы тура
, ал (10) кіші интервалы тура
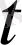 болады. Сондықтан (10) жарты интервалдар арасынан (8) сандарынан екеуін құрайтын жарты интервал табылады. Ол келесі сандар болсын
болады. Сондықтан (10) жарты интервалдар арасынан (8) сандарынан екеуін құрайтын жарты интервал табылады. Ол келесі сандар болсын
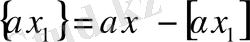 ,
,
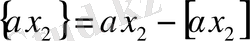
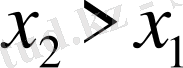
онда
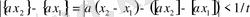 (11)
(11)
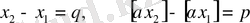
деп белгілейік.
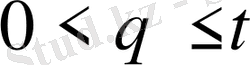 болатыны анық. Сондықтан (11) теңсіздігінен қарастырылып отырған жағдайдағы теорема тұжырымы шығатын
болатыны анық. Сондықтан (11) теңсіздігінен қарастырылып отырған жағдайдағы теорема тұжырымы шығатын
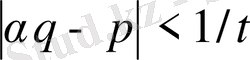 ,
,
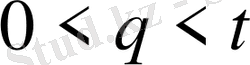 (12)
(12)
теңсіздігі шығады. Жалпы жағдайда
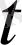 кез келген нақты сан болғанда дәлелдеу едәуір қиындай түседі. Онда
кез келген нақты сан болғанда дәлелдеу едәуір қиындай түседі. Онда
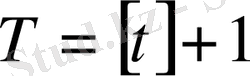 бүтін санын және
бүтін санын және
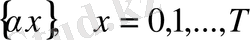 үшін
үшін
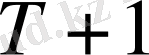 сандарын қарастыру керек. Содан кейін
сандарын қарастыру керек. Содан кейін
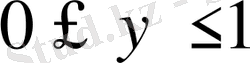 кесіндісін
кесіндісін
 бөлікке бөлеміз. Бірінші жағдайдағыдай тұжырымдай отырып алатын теңсіздігіміз
бөлікке бөлеміз. Бірінші жағдайдағыдай тұжырымдай отырып алатын теңсіздігіміз
 (13)
(13)
болады. Осыдан, егер қарастырылып отырған нүктелердің екеуі
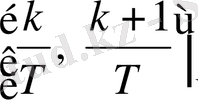 бөліктік кесіндіде жатады,
бөліктік кесіндіде жатады,
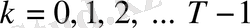 .
.
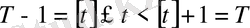
болғандықтан, онда (13) теңсіздігінен теореманы анықтайтын (12) теңсіздігі шығады.
Екінші дәлелдеуде
 болғандағы жағдай бар болатынын ескере кетейік.
болғандағы жағдай бар болатынын ескере кетейік.
Егер
 ,
,
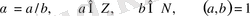
болса, онда кез келген
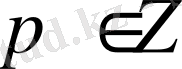 және
және
 кезінде келесі теңсіздік орындалады:
кезінде келесі теңсіздік орындалады:
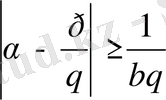
Сондықтан
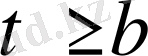 кезінде (7) теңсіздігінің тек
кезінде (7) теңсіздігінің тек
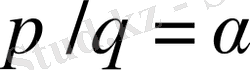 тривалды шешімі болады. Сондықтан (7) теңсіздігінің барлық тривалды емес шешімінің бөлімдері шектеулі. Бұл
тривалды шешімі болады. Сондықтан (7) теңсіздігінің барлық тривалды емес шешімінің бөлімдері шектеулі. Бұл
 кезінде Дирихле теоремасы өз бөлімдерімен рационал сандарды рационал сандар жуықтау жөнінде мәлімет беретін тұжырым болып табылады.
кезінде Дирихле теоремасы өз бөлімдерімен рационал сандарды рационал сандар жуықтау жөнінде мәлімет беретін тұжырым болып табылады.
Егер
 иррационалды болса, онда
иррационалды болса, онда
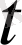 өсуімен (7) теңсіздігінің бөлімдер шешімі де өседі.
өсуімен (7) теңсіздігінің бөлімдер шешімі де өседі.

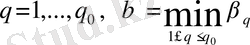
мұнда
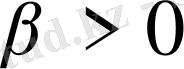 . Онда кез келген
. Онда кез келген
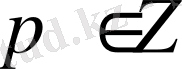 және
және
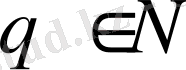 кезінде келесі теңсіздік орындалады.
кезінде келесі теңсіздік орындалады.
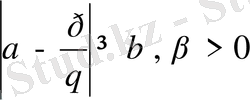
Бірақ жеткілікті үлкен
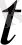 кезіндегі соңғы теңсіздік (7) теңсіздігіне қарама-қарсы. Бұдан,
кезіндегі соңғы теңсіздік (7) теңсіздігіне қарама-қарсы. Бұдан,
 иррационал сан болғанда мүмкін
иррационал сан болғанда мүмкін
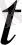 мәні үшін (7) теңсіздігінің барлық бөлімдер шешімдері шектеусіз.
мәні үшін (7) теңсіздігінің барлық бөлімдер шешімдері шектеусіз.
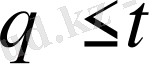 ескере отырып (7) теңсіздігінен келесі теңсіздікті аламыз.
ескере отырып (7) теңсіздігінен келесі теңсіздікті аламыз.
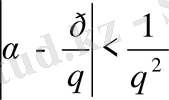 (14)
(14)
Жоғарыда дәлелденгеннен,
 иррационалдық саны үшін (14) теңсіздігінің алдын-ала берілген саннан үлкен бөліммен шешімі бар болады.
иррационалдық саны үшін (14) теңсіздігінің алдын-ала берілген саннан үлкен бөліммен шешімі бар болады.
Теорема 1.
Кез келген
 иррационал саны үшін (14) теңсіздігінің
иррационал саны үшін (14) теңсіздігінің
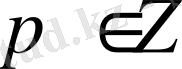 және
және
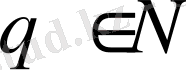 сандарында шексіз шешімдері бар.
сандарында шексіз шешімдері бар.
Бұл теорема барлық иррациолнал сандар рационал сандармен жуықтаудың дәрежелік реті 2 ге тең екенін көрсетеді.
 дан кез келген сандармен жуықтау дәрежелік ретін жіберетін иррационалды сандар бар болады. Мұндай сандардың мысалын тез жинақталатын қатарлар арқылы құруға болады.
дан кез келген сандармен жуықтау дәрежелік ретін жіберетін иррационалды сандар бар болады. Мұндай сандардың мысалын тез жинақталатын қатарлар арқылы құруға болады.
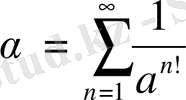 ,
,
 Equation. 3 (15)
Equation. 3 (15)
Қатардың алғашқы
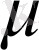 -қосындысын алып,
-қосындысын алып,

белгілейік Онда,
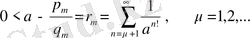
Бірақ

Сондықтан
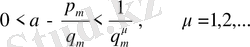
Соңғы теңсіздіктен кез келген
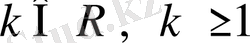 кезінде
кезінде
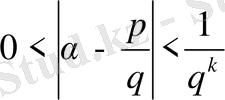 (16)
(16)
теңсіздігінің
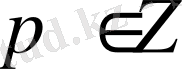 және
және
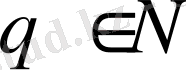 сандарында шешімі бар. Бірақ
сандарында шешімі бар. Бірақ
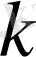 мәнімен берілген (16) теңсіздігінің әрбір шешімі кез келген
мәнімен берілген (16) теңсіздігінің әрбір шешімі кез келген
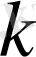 дан кіші мәнімен тағы басқа сол теңсіздіктің шешімі болып табылады. Бұдан кез келген
дан кіші мәнімен тағы басқа сол теңсіздіктің шешімі болып табылады. Бұдан кез келген
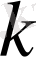 кезінде (16) теңсіздігінің
кезінде (16) теңсіздігінің
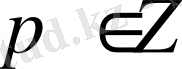 және
және
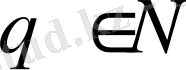 сандарында шексіз көп шешімі бар екені шығады.
сандарында шексіз көп шешімі бар екені шығады.
1-теоремадан
 - иррационалды сандарын келесі түрде жазуға болады.
- иррационалды сандарын келесі түрде жазуға болады.
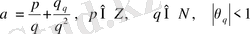 (17)
(17)
мұнда
 бөлімі
бөлімі
 дегі кез келген емес сан, бірақ қалауымыз бойынша үлкен қылдырып алуға болады. (17) түріндегі иррационал сандары сандар теориясында кең қолданылады.
дегі кез келген емес сан, бірақ қалауымыз бойынша үлкен қылдырып алуға болады. (17) түріндегі иррационал сандары сандар теориясында кең қолданылады.
 иррационалды сандарының келесідей ондық жіктелуі болсын делік.
иррационалды сандарының келесідей ондық жіктелуі болсын делік.

Әдетте
 ны
ны
 ға жуық санмен ауыстыра отырып, оны ондық жіктелудің кесіндісіне ауыстырады.
ға жуық санмен ауыстыра отырып, оны ондық жіктелудің кесіндісіне ауыстырады.
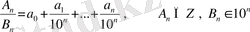 ,
,
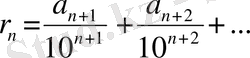
белгілейік, онда
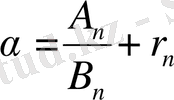
Бірақ
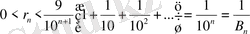 ,
,
және сондықтан
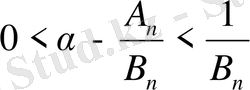
Бұдан
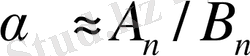 ауыстыру кезіндегі қателік
ауыстыру кезіндегі қателік
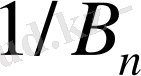 нен аспайтыны шығады.
нен аспайтыны шығады.
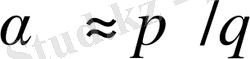 ауыстыруы, мұнда
ауыстыруы, мұнда
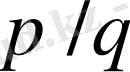 (14) теңсіздігінің шешімі болып табылады, дегенмен қателігі
(14) теңсіздігінің шешімі болып табылады, дегенмен қателігі
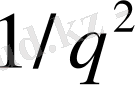 тан аспайды.
тан аспайды.
1. 2. Фарей қатары.
Бұл параграфта рационал бөлшектерді қарастыра отырып, олардың ішінен оң бөлшектерін аламыз.
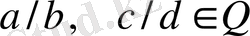 екі бөлшектің медиантасы деп
екі бөлшектің медиантасы деп
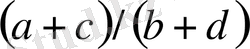 бөлшегі аталады
Лемма 1.
Әр түрлі екі бөлшектің медиантасы екеуінің әр біреуінен өзгеше және олардың арасында жатады.
бөлшегі аталады
Лемма 1.
Әр түрлі екі бөлшектің медиантасы екеуінің әр біреуінен өзгеше және олардың арасында жатады.
Дәлелдеуі:
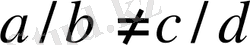 болсын. Анықтылық үшін
болсын. Анықтылық үшін
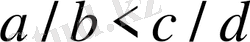 дейік. Онда
дейік. Онда
 және
және
 шарты бойынша
шарты бойынша
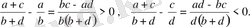
ал,
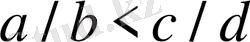 тұжырымы бойынша
тұжырымы бойынша
 теңсіздігі орындалады. Сондықтан
теңсіздігі орындалады. Сондықтан
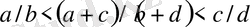
Егер
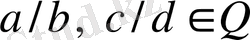 екі бөлшектеі үшін
екі бөлшектеі үшін
 орындалса, онда оларды бөлшектердің нормалдық жұбы деп атаймыз.
орындалса, онда оларды бөлшектердің нормалдық жұбы деп атаймыз.
Лемма 2.
Егер
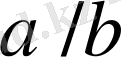 және
және
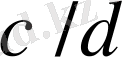 бөлшектердің нормалды жұптары болса, онда олардың әрқайсысы қысқарылмайтын болып табылады.
бөлшектердің нормалды жұптары болса, онда олардың әрқайсысы қысқарылмайтын болып табылады.
Дәлелдеуі:
Лемма шарты бойынша
 теңсіздігі орындалады, бұдан
теңсіздігі орындалады, бұдан
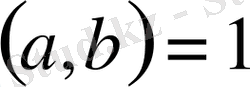 және
және
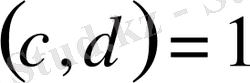 шығатыны анық.
шығатыны анық.
Лемма 3.
Егер
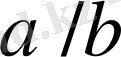 және
және
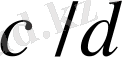 бөлшектердің нормалды жұптары болса, онда
бөлшектердің нормалды жұптары болса, онда
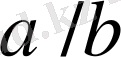 ,
,
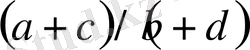 және
және
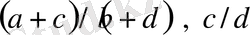 жұптардың әр біреуі бөлшектердің нормалды жұптары болып табылады.
жұптардың әр біреуі бөлшектердің нормалды жұптары болып табылады.
Дәлелдеуі:
 деп белгілейік. Онда 1-лемма бойынша
деп белгілейік. Онда 1-лемма бойынша
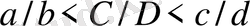 теңдігі орындалады. Әрі қарай
теңдігі орындалады. Әрі қарай
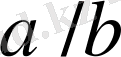 және
және
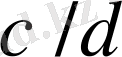 бөлшектердің нормалды жұптарына қарай
бөлшектердің нормалды жұптарына қарай
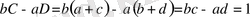
ұқсас түрде
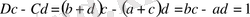
Лемма дәлелденді.
Лемма 4:
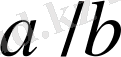 және
және
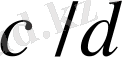 бөлшектердің нормалды жұптары, ал
бөлшектердің нормалды жұптары, ал
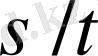 келесі теңсіздікті
келесі теңсіздікті
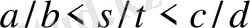 (18)
(18)
қанағаттандыратын қысқармайтын бөлшек болсын. Онда
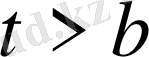 және
және
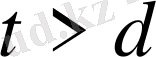 болады.
болады.
Дәлелдеуі:
Лемма шарты бойынша
 болады. Сондықтан
болады. Сондықтан
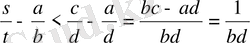 (19)
(19)
бұдан (19) теңсіздігінің екі жағын да
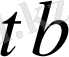 ға көбейте отырып
ға көбейте отырып
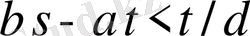 болатынын, немесе
болатынын, немесе
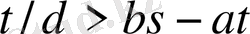 (20)
(20)
болатынын табамыз.
Бірақ (18) шартынан
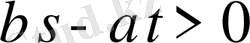 теңдігі орындалатыны шығады. Онда
теңдігі орындалатыны шығады. Онда
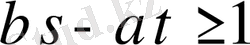 (21)
(21)
болады. (20) және (21) теңдігінен
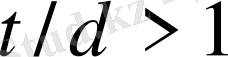 және
және
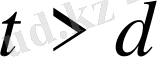 болатынын аламыз.
болатынын аламыз.
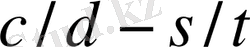 айырымын қарастыра отырып
айырымын қарастыра отырып
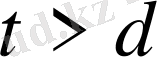 болатынын дәлелдейміз.
болатынын дәлелдейміз.
Анықтама:
 үшін
үшін
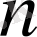 -ретті Фарей қатары деп
-ретті Фарей қатары деп
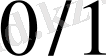 және
және
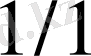 бөлшектерінің арасындағы бөлімдері
бөлшектерінің арасындағы бөлімдері
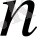 нен аспайтын қысқарылмайтын дұрыс бөлшектердің өсу ретімен жасалған жиынды айтамыз.
нен аспайтын қысқарылмайтын дұрыс бөлшектердің өсу ретімен жасалған жиынды айтамыз.
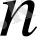 -ретті Фарей қатарын
-ретті Фарей қатарын
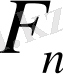 арқылы белгілейтін боламыз, ал Фарей қатарын құру қиын емес. Мысалы,
арқылы белгілейтін боламыз, ал Фарей қатарын құру қиын емес. Мысалы,

Егер келесі
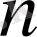 мәндер үшін осы қатарды құра беретін болсақ, онда әр қадам бойынша есеп қиындай түседі.
мәндер үшін осы қатарды құра беретін болсақ, онда әр қадам бойынша есеп қиындай түседі.
Фарей қатарын рекурентті құруға мүмкіндік беретін әдісті көрсетейік және олардың кейбір қасиеттерін қарастырайық. Өлшемдері өсу ретімен орналасқан бөлшектер жиынының

рекурентті шексіз жиынын анықтайық.
 бөлшегі
бөлшегі
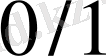 және
және
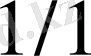 екі бөлшектен тұрсын. Әрі қарай, егер
екі бөлшектен тұрсын. Әрі қарай, егер
 жиыны анық болса, онда
жиыны анық болса, онда
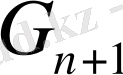 келесі түрде анықталады.
келесі түрде анықталады.
 нен
нен
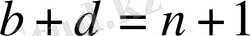 болатын барлық
болатын барлық
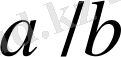 және
және
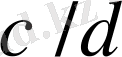 көрші бөлшектер жұптарын алайық және олардың
көрші бөлшектер жұптарын алайық және олардың
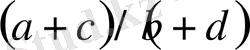 медиантасын
медиантасын
 ге қосайық. 1-лемма бойынша бұл медианталар
ге қосайық. 1-лемма бойынша бұл медианталар
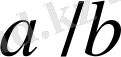 және
және
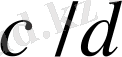 сәйкес бөлшектер арасында орналасады.
сәйкес бөлшектер арасында орналасады.
Берілген анықтамадан
 дегі барлық бөлшектер бөлгіші
дегі барлық бөлшектер бөлгіші
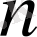 нен аспайтыны, ал кез келген 2 көрші бөлшектер бөлгіштердің қосындысы
нен аспайтыны, ал кез келген 2 көрші бөлшектер бөлгіштердің қосындысы
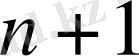 - ден аз емес екені шығатыны айқын.
- ден аз емес екені шығатыны айқын.
Егер
 жиынын тізбектей құрып отырсақ, онда олар
жиынын тізбектей құрып отырсақ, онда олар
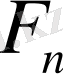 Фарей қатарымен сәйкес келетінін көруге болады. Енді осы фактының кез келген
Фарей қатарымен сәйкес келетінін көруге болады. Енді осы фактының кез келген
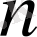 кезінде орны болатынын дәлелдейік. Онда Фарей қатарын рекуренттік құру әдісімен аламыз.
кезінде орны болатынын дәлелдейік. Онда Фарей қатарын рекуренттік құру әдісімен аламыз.
Лемма 5:
 жиынында кез келген
жиынында кез келген
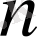 үшін әрбір көрші бөлшектер жұбы бөлшектердің нормалды жұбы болып табылады.
үшін әрбір көрші бөлшектер жұбы бөлшектердің нормалды жұбы болып табылады.
Дәлелдеуі:
Лемманы
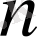 бойынша индукциямен дәлелдейік.
бойынша индукциямен дәлелдейік.
 кезінде тұжырым айқын. Бұл
кезінде тұжырым айқын. Бұл
 үшін дұрыс деп қабылдаймыз, және ол
үшін дұрыс деп қабылдаймыз, және ол
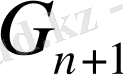 үшін де орындалатынын дәлелдейік.
үшін де орындалатынын дәлелдейік.
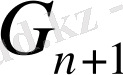 ді анықтау бойынша 3 жағдай болуы мүмкін.
ді анықтау бойынша 3 жағдай болуы мүмкін.
1) .
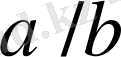 және
және
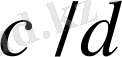
 дегі көрші бөлшектер болып табылады. Онда олар үшін лемма тұжырымы индукция бойынша орындалады.
дегі көрші бөлшектер болып табылады. Онда олар үшін лемма тұжырымы индукция бойынша орындалады.
2) .
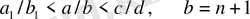 теңсіздігі орындалады, мұнда
теңсіздігі орындалады, мұнда
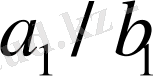 және
және
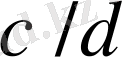
 дегі екі көрші бөлшектер, ал
дегі екі көрші бөлшектер, ал
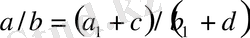 бөлшегі
бөлшегі
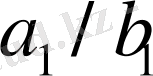 және
және
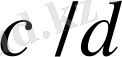 бөлшектерінің медиантасы болып табылады.
бөлшектерінің медиантасы болып табылады.
3) .
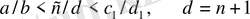 теңсіздігі орындалады, мұнда
теңсіздігі орындалады, мұнда
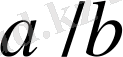 және
және
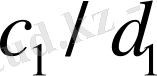
 дегі екі көрші бөлшектер, ал
дегі екі көрші бөлшектер, ал
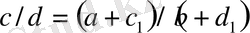 бөлшегі
бөлшегі
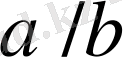 және
және
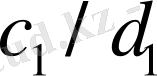 бөлшектерінің медиантасы болып табылады.
бөлшектерінің медиантасы болып табылады.
Осылайша лемманың тұжырымы
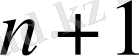 мәні үшін орындалады, ал индукция бойынша барлық
мәні үшін орындалады, ал индукция бойынша барлық
 мәндер үшін орындалады.
мәндер үшін орындалады.
Лемма 6:
Кез келген
 үшін
үшін

Дәлелдеуі:
 ді қарастырайық.
ді қарастырайық.
 кезінде лемма тұжырымы айқын.
кезінде лемма тұжырымы айқын.
 болсын . 5-лемма бойынша
болсын . 5-лемма бойынша
 дегі екі көрші бөлшектердің нормалды бөлшектер жұбы бар болады. Сондықтан 2-лемма бойынша олар қасқармайды.
дегі екі көрші бөлшектердің нормалды бөлшектер жұбы бар болады. Сондықтан 2-лемма бойынша олар қасқармайды.
 анықтау бойынша бұл жиын
анықтау бойынша бұл жиын
 болғанда
болғанда
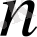 ге тең бөлгіштер қосындысымен
ге тең бөлгіштер қосындысымен
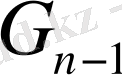 -ге тізбектей қосу жолы арқылы алынады, және сондықтан
-ге тізбектей қосу жолы арқылы алынады, және сондықтан
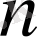 нен аспайтын бөлімдері бар бөлшектерден тұрады, яғни
нен аспайтын бөлімдері бар бөлшектерден тұрады, яғни

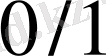 және
және
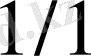 бөлшектерден тұрады және 1-лемма бойынша
бөлшектерден тұрады және 1-лемма бойынша
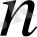 нен аспайтын
нен аспайтын
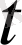 бөлгішімен
бөлгішімен
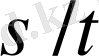 оң қысқармайтын дұрыс бөлшектерден тұрады. Барлық осындай
оң қысқармайтын дұрыс бөлшектерден тұрады. Барлық осындай
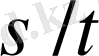 бөлшектер
бөлшектер
 құрамына кіретінін дәлелдейік. Онда
құрамына кіретінін дәлелдейік. Онда
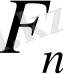 анықтау бойынша
анықтау бойынша
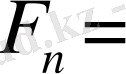
 .
.
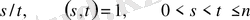 кез келген бөлшек болсын. Егер
кез келген бөлшек болсын. Егер
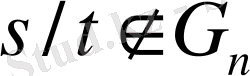 десек, онда
десек, онда
 де
де
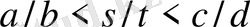 , мұнда
, мұнда
 және
және
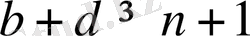 болатындай
болатындай
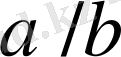 және
және
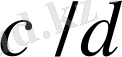 екі көрші бөлшектер табылады. 5-лемма бойынша
екі көрші бөлшектер табылады. 5-лемма бойынша
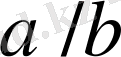 және
және
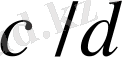 бөлшектердің нормалды жұптары бар болса, онда 3 және 2 -леммалар бойынша
бөлшектердің нормалды жұптары бар болса, онда 3 және 2 -леммалар бойынша
 болатындай
болатындай
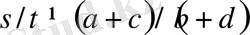 болады, ал
болады, ал
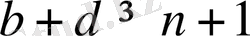 яғни, немесе
яғни, немесе
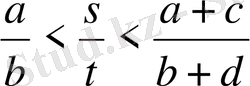
немесе
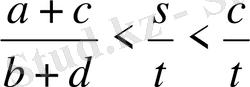
болады.
3-лемма бойынша
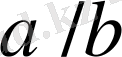 ,
,
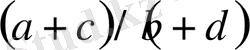 және
және
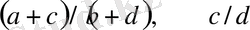 әрбір жұп бөлшектердің нормалды жұбы бар болса, онда 4-лемма бойынша
әрбір жұп бөлшектердің нормалды жұбы бар болса, онда 4-лемма бойынша
 қарама-қарсы
қарама-қарсы
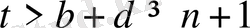 болады. Алынған қарама-қайшылық дәлелденді.
болады. Алынған қарама-қайшылық дәлелденді.
Салдар:
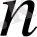 ретті
ретті
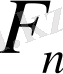 Фарей қатарындағы кез келген екі көрші бөлшектер нормалды бөлшектер жұбы болады.
Фарей қатарындағы кез келген екі көрші бөлшектер нормалды бөлшектер жұбы болады.
Дирихле теоремасын дәлелдеу:
 кезіндегі жағдайды қарастырған жеткілікті, кері жағдайда
кезіндегі жағдайды қарастырған жеткілікті, кері жағдайда
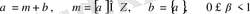
онда
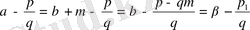
 , ал
, ал
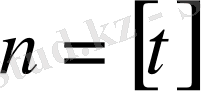 болсын.
болсын.
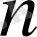 - ретті Фарей қатарын қарастырамыз.
- ретті Фарей қатарын қарастырамыз.
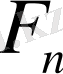 -де
-де
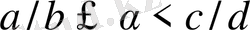 болатындай
болатындай
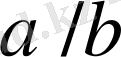 және
және
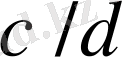 екі көрші бөлшектер табылады. Онда
екі көрші бөлшектер табылады. Онда
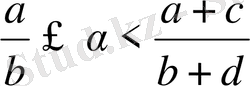
немесе
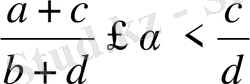
болады.
Сондықтан Фарей қатарының қасиеті бойынша
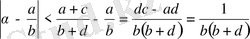
немесе
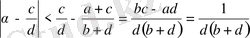
Бірақ
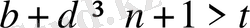 . Онда
. Онда
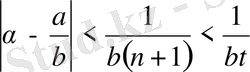
немесе

болады.
Бірінші жағдайда
 қоямыз, ал екінші жағдайда
қоямыз, ал екінші жағдайда
 қоямыз. Сонда келесі теңсіздік орындалады.
қоямыз. Сонда келесі теңсіздік орындалады.
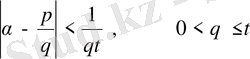
Теорема дәлелденді.
Фарей қатарының көмегімен рационалды бөлшектермен нақты сандарды жуықтау жөніндегі есептермен байланысты диофанттық жуықтау теориясынан басқа да теоремалар тізімі дәлелденеді. Олардың дәлелдеулерінде берілген
 иррационал санына жеткілікті тез жиналатын Фарей қатарынан тізбекті бөліп алуға болатын факт қолданылады.
иррационал санына жеткілікті тез жиналатын Фарей қатарынан тізбекті бөліп алуға болатын факт қолданылады.
 саны
саны
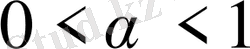 болатындай иррационал сан болсын.
болатындай иррационал сан болсын.
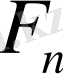 дегі кез келген
дегі кез келген
 кезінде
кезінде
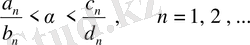
болатындай
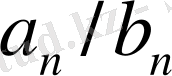 және
және
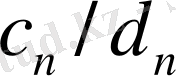 көрші бөлшектер жұбы табылады.
көрші бөлшектер жұбы табылады.
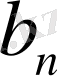 және
және
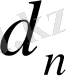 сандары
сандары
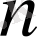 өсуімен кемімейтіні анық,
өсуімен кемімейтіні анық,
 және
және
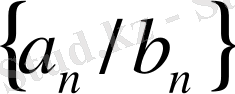 және
және
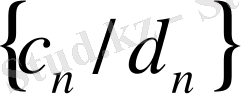 тізбектері
тізбектері
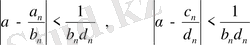
болатындай
 ға оңынан және солынан жақсы жуықтау болып табылады.
ға оңынан және солынан жақсы жуықтау болып табылады.
ІІ-ТАРАУ.
НАҚТЫ САНДАРДЫ ҮЗДІКСІЗ БӨЛШЕКТЕРМЕН ЖУЫҚТАУ.
2. 1. Үздіксіз бөлшектердің лайықты бөлшектері және олардың негізгі қасиеттері
Анықтама . Ақырлы үздіксіз бөлшектер деп келесі өрнекті айтамыз:
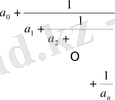 (1)
(1)
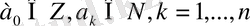
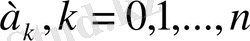 сандары үздіксіз бөлшектің элементтері, ал
сандары үздіксіз бөлшектің элементтері, ал
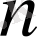 (1) үздіксіз бөлшегінің ұзындығы деп аталады.
(1) үздіксіз бөлшегінің ұзындығы деп аталады.
 болғанда
0
- мүшелі үздіксіз бөлшегі
а
0
түрінде болады. (1) үздіксіз бөлшегін тағы да келесі түрде бейнелейді:
болғанда
0
- мүшелі үздіксіз бөлшегі
а
0
түрінде болады. (1) үздіксіз бөлшегін тағы да келесі түрде бейнелейді:
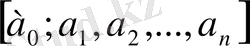
Ақырлы үздіксіз бөлшегін төменнен жоғары қарай
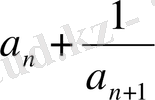 бөлшегін алдымен ортақ бөлімге келтіріп одан кейін аударып отырып жиырсақ, онда рационал сан болады.
бөлшегін алдымен ортақ бөлімге келтіріп одан кейін аударып отырып жиырсақ, онда рационал сан болады.
Анықтама. Ақырсыз үздіксіз бөлшек деп келесі өрнекті айтамыз:
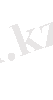
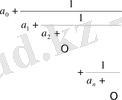 (2)
(2)
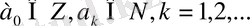
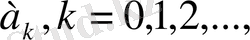 сандарын ақырсыз үздіксіз бөлшектің элементтері деп атайды.
сандарын ақырсыз үздіксіз бөлшектің элементтері деп атайды.
Ақырсыз үздіксіз бөлшек (2) келесі түрмен бейнелейді:
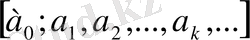
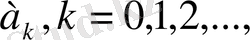 натурал элементтерімен. Ақырлы және ақырсыз үздіксіз бөлшектердің кластары кеңінен қарасақ, бұлардың элементтері бір немесе бірнеше айнымалылардың функциялары және комплекс немесе нақты сандар болып табылады. (2) ақырсыз үздіксіз бөлшектің
натурал элементтерімен. Ақырлы және ақырсыз үздіксіз бөлшектердің кластары кеңінен қарасақ, бұлардың элементтері бір немесе бірнеше айнымалылардың функциялары және комплекс немесе нақты сандар болып табылады. (2) ақырсыз үздіксіз бөлшектің
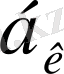 лайықты бөлшектері деп ақырлы үздіксіз бөлшектерді айтады.
лайықты бөлшектері деп ақырлы үздіксіз бөлшектерді айтады.
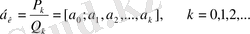
1-теорема . Кез келген рационал санды ақырлы, ал иррационал санды ақырсыз үздіксіз бөлшек түрінде көрсетуге болады.
Шынында да, айталық
а
рационал сан болсын,
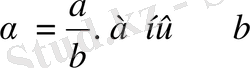 ға бөліп,
ға бөліп,
 (3)
(3)
екенін табамыз. Мұндағы
 саны
саны
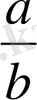 дан аспайтын ең үлкен бүтін сан, яғни
дан аспайтын ең үлкен бүтін сан, яғни
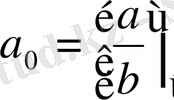 екені түсінікті.
екені түсінікті.
(3) теңдікті
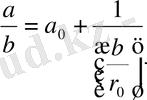 (4)
(4)
түрінде қайта жазып,
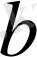 ні
ні
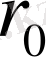 ге бөлеміз:
ге бөлеміз:
 (5)
(5)
Мұндағы
 саны
саны
 ден аспайтын ең үлкен бүтін сан болады, яғни
ден аспайтын ең үлкен бүтін сан болады, яғни
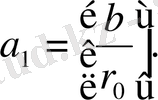 (5) -ден
(5) -ден
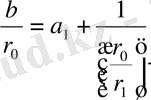 мәнін тауып, (4) -ге қоямыз.
мәнін тауып, (4) -ге қоямыз.
Сонда
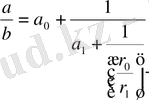
 (6)
(6)
Енді
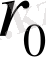 ді
ді
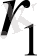 ге бөлеміз:
ге бөлеміз:

Мұндағы
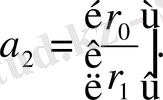 Бұндан
Бұндан
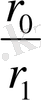 -нің мәнін
-нің мәнін
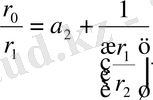
Тауып, (6) -ге қойсақ, мынау шығады:
 (7)
(7)
Тағыда
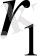 ді
ді
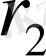 ге бөлеміз:
ге бөлеміз:

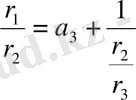 -нің мәнін (7) -ға қойып,
-нің мәнін (7) -ға қойып,
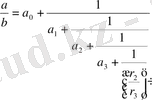 (8)
(8)
аламыз.
Бұдан әрі
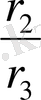 қатынасын тауып,
қатынасын тауып,

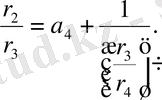
Жоғарыдағы сияқты, (8) -ге қоямыз және осы процесті соза береміз. Бұл процесс ақырлы және ол Евклид алгоритмін береді:
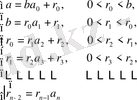
Теңдіктер мен
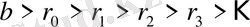 теңсіздіктердің саны ақырлы болғандықтан, міндетті түрде алдыңғысы соңғысына қалдықсыз бөлінетін
теңсіздіктердің саны ақырлы болғандықтан, міндетті түрде алдыңғысы соңғысына қалдықсыз бөлінетін
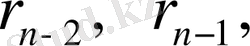 қалдықтары шығатынын көрсетеді:
қалдықтары шығатынын көрсетеді:
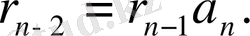
Олай болса,
 рационал санын көрсететін үздіксіз бөлшек саны ақырлы
рационал санын көрсететін үздіксіз бөлшек саны ақырлы
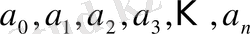 толымсыз бөлінділерін ғана қамтиды, яғни
толымсыз бөлінділерін ғана қамтиды, яғни
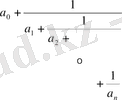
Айталық енді
,
 иррационал сан болсын.
а
0
арқылы
иррационал сан болсын.
а
0
арқылы
 дан аспайтын ең үлкен бүтін санды белгілейік, яғни
дан аспайтын ең үлкен бүтін санды белгілейік, яғни
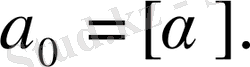 сонда
сонда
 (9)
(9)
Мұнда
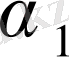 саны
саны
 нің бөлшек бөлігі және ол иррационал сан болады, әйтпесе
нің бөлшек бөлігі және ол иррационал сан болады, әйтпесе
 рационал сан болған болар еді. Айтадық
рационал сан болған болар еді. Айтадық
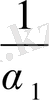 нің бүтін бөлігі
нің бүтін бөлігі
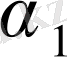 болсын, сонда
болсын, сонда
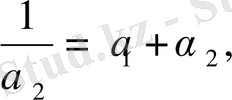 мұнда
мұнда
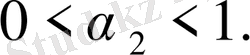 (10)
(10)
Дәл осы сияқты, егерде
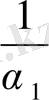 нің бүтін бөлігі
нің бүтін бөлігі

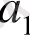 болса, онда
болса, онда
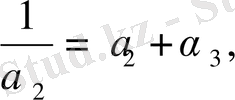
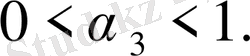 (11)
(11)
Жоғарыдағыдай, төмендегі теңдіктерді табамыз:
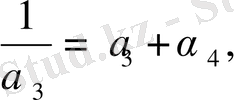
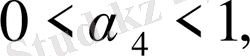
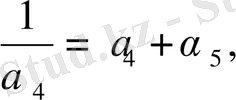
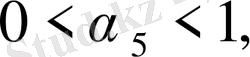 (12)
(12)
. . .
Мұндағы
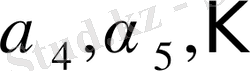 иррационал сандар
иррационал сандар
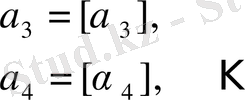
 иррационал сан болғандықтан, сандардың бүтін бөлігін бөлу процесі шектеулі бола алмайды.
иррационал сан болғандықтан, сандардың бүтін бөлігін бөлу процесі шектеулі бола алмайды.
(9), (10), (11) және (12) теңдіктерінен біртіндеп;
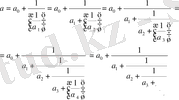
табамыз.
Сөйтіп, а үшін ақырсыз үздіксіз бөлшек аламыз. Теорема дәлелденді.
Тағы да ақырлы (1) үздіксіз бөлшегін қайта қарастырамыз. Үздіксіз бөлшектегі
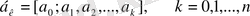 (13)
(13)
Ақырлы үздіксіз бөлшекті (1) үздіксіз бөлшектің
 -шы ретті лайықты бөлшегі деп атайды.
-шы ретті лайықты бөлшегі деп атайды.
(1) үздіксіз бөлшектің n -ретті лайықты бөлшегі осы бөлшекке сәйкес келеді.
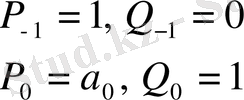 (14)
(14)
Әр қарай рекурентті түрде анықтаймыз.
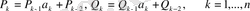 (15)
(15)
(15) теңсіздігінен анық түрде мынау шығады
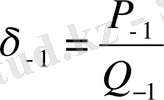 немесе
немесе
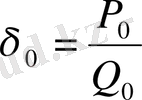
Индукциямен
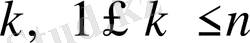 индексі бойынша дәлелдейміз
индексі бойынша дәлелдейміз
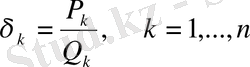 (16)
(16)
 болғанда (14) және (15) теңсіздіктерінен мынау шығады:
болғанда (14) және (15) теңсіздіктерінен мынау шығады:
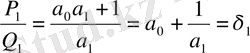
Айталық, (15) теңсіздігі қандайда бір
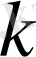 мәні үшін
мәні үшін
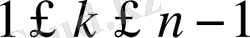 және ол
және ол
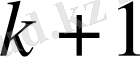 мәні үшін де дұрыс.
мәні үшін де дұрыс.
Теңсіздіктерден
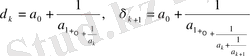 (17)
(17)
Осыдан, егер соңғы теңсіздіктің оң жағындағы
 ны
ны
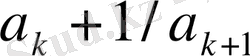 ге өзгертсек, онда
ге өзгертсек, онда
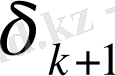 үшін
үшін
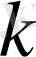 -өрнек шығады.
-өрнек шығады.
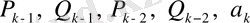 -дан тәуелсіз (рекурентті құрылымда олар тек
-дан тәуелсіз (рекурентті құрылымда олар тек
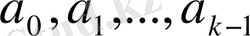 арқылы анықталады), онда
арқылы анықталады), онда

(14) теңсіздігін қолдана отырып мынаны аламыз
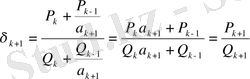
Бұл (16) теңсіздігі
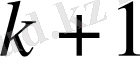 мағынасы үшін дұрыс, ал индукция бойынша
мағынасы үшін дұрыс, ал индукция бойынша
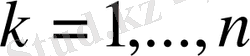 барлық мағыналары үшін дұрыс. Сонымен, мына теңдіктер орындалады.
барлық мағыналары үшін дұрыс. Сонымен, мына теңдіктер орындалады.
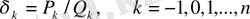 (18)
(18)
Осындағы
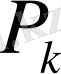 немесе
немесе
 (14) және (15) теңсіздіктерімен анықталады.
(14) және (15) теңсіздіктерімен анықталады.
 болғанда
болғанда
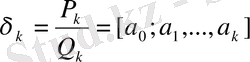
Осымен (1) әрбір ақырлы үздіксіз бөлшек
 дан алынған сан және үздіксіз бөлшектің элементтері бойынша оның мәндерін табуға мүмкіндік береді.
дан алынған сан және үздіксіз бөлшектің элементтері бойынша оның мәндерін табуға мүмкіндік береді.
2-теорема.
Тетелес
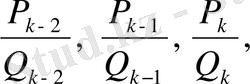 үш лайықты бөлшектің алымдары
үш лайықты бөлшектің алымдары
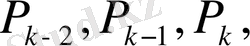 мен бөлімдері
мен бөлімдері
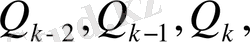 өз ара
өз ара
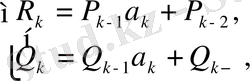 (19)
(19)
қатысы арқылы байланысады, мұндағы
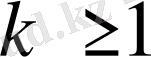
Шынында да, айталық, ақырлы ақырсыз үздіксіз бөлшек берілсін:
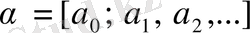 .
.
Егер
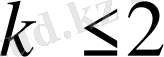 болса,
болса,
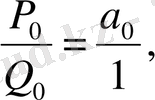
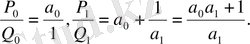
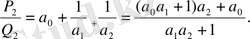
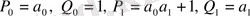 болғандықтан,
болғандықтан,
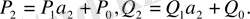
Сөйтіп,
 болғанда (19) қатыс орынды болады. айталық (19) қатыс
болғанда (19) қатыс орынды болады. айталық (19) қатыс
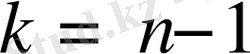 болғанда дұрыс болсын
болғанда дұрыс болсын
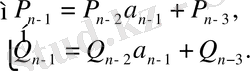 (20)
(20)
Енді (19) қатыстың
 үшін орынды екендігін көрсетейік. Ол үшін
үшін орынды екендігін көрсетейік. Ол үшін
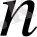 нөмірлі лайықты
нөмірлі лайықты
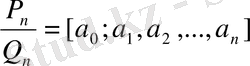
бөлшекті алып,
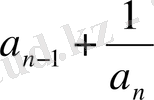 қосындысын
қосындысын
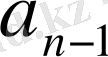 деп белгілейік. Сонда біз
деп белгілейік. Сонда біз
 толымсыз бөлінділерден тұратын
толымсыз бөлінділерден тұратын
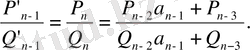
Мұндағы
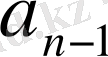 -ның орнына оның мәні
-ның орнына оның мәні
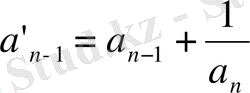
қосындыны қойып,

табамыз, немесе (3) теңдікті алсақ,
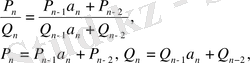
шығады. Онда (20) теңдіктер кез келген
 үшін орындалады. Осымен теорема толық дәлелденді.
үшін орындалады. Осымен теорема толық дәлелденді.
(19) формулалар
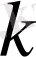 нің өсуіне байланысты лайықты бөлшектің алымы да, бөлімі де өсетіндігін көрсетеді, яғни
нің өсуіне байланысты лайықты бөлшектің алымы да, бөлімі де өсетіндігін көрсетеді, яғни
 барлық
барлық
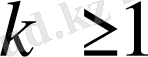 үшін.
үшін.
(19) формулалардың қолданылуын мысал арқылы көрсетейік:
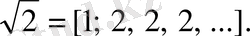
Алғашқы екі лайықты мәні олардың анықтамаларынан тікелей шығады:
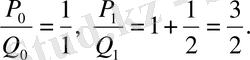
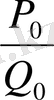 мен
мен
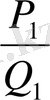 мәндері бойынша (19) қатысты пайдаланып әуелі
мәндері бойынша (19) қатысты пайдаланып әуелі
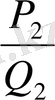 -нің мәнін, содан соң
-нің мәнін, содан соң
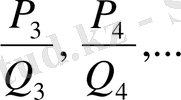 мәндерін оп - оңай тауып алуға болады. атап айтқанда:
мәндерін оп - оңай тауып алуға болады. атап айтқанда:

3-теорема
. Егерде
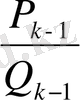 мен
мен
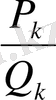 кез келген тетелес тұрған екі лайықты бөлшек болса, онда
кез келген тетелес тұрған екі лайықты бөлшек болса, онда
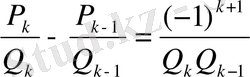
немесе
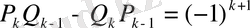 (21)
(21)
қатысы орынды.
Шынында да,
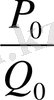 мен
мен
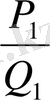 лайықты бөлшектері үшін (21) қатыстың орынды екендігін тікелей тексеру арқылы байқаймыз:
лайықты бөлшектері үшін (21) қатыстың орынды екендігін тікелей тексеру арқылы байқаймыз:
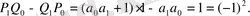
Айталық,
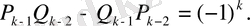 (22)
(22)
Онда
 өрнегіне (19) қатыстан
өрнегіне (19) қатыстан
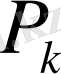 мен
мен
 нің мәнін алып қойсақ:
нің мәнін алып қойсақ:
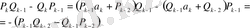
немесе (22) -ге сүйенсек:
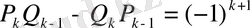
Екенін табамыз. Дәлелдеу керегі де осы еді. (21) қатыстың біріншісі екіншісін
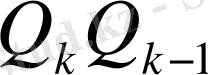 ге бөлуден шығады.
ге бөлуден шығады.
4-теорема. Лайықты бөлшектер - қысқармайтын бөлшектер.
Шынында, айталық
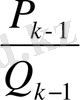 мен
мен
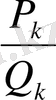 (18) үздіксіз бөлшектің көршілес екі лайықты бөлшектері болсын. онда 3-теоремадағы (21) қатыстың екіншісі бойынша:
(18) үздіксіз бөлшектің көршілес екі лайықты бөлшектері болсын. онда 3-теоремадағы (21) қатыстың екіншісі бойынша:
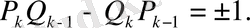
Бұл қатыстан
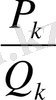 лайықты бөлшегінің алымы
лайықты бөлшегінің алымы
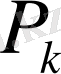 мен бөлімі
мен бөлімі
 -нің 1-ден басқа ортақ бөлгіші жоқ екендігі көрініп тұр.
-нің 1-ден басқа ортақ бөлгіші жоқ екендігі көрініп тұр.
5-теорема.
Барлық
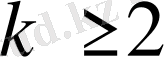 сандары үшін
сандары үшін
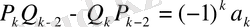
немесе
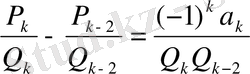 (23)
(23)
қатысы орынды.
Дәлелдеу үшін
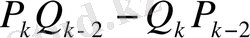 өрнегіндегі
өрнегіндегі
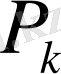 мен бөлімі
мен бөлімі
 -нің (19) -ден мәндерін қояйық. Сонда
-нің (19) -ден мәндерін қояйық. Сонда
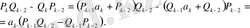
Бұдан (22) -ге сүйенсек:
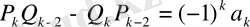 .
.
Мұны
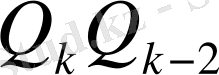 ге мүшелеп бөлсек, (23) қатыстың екіншісін аламыз.
ге мүшелеп бөлсек, (23) қатыстың екіншісін аламыз.
Дәлелденген (23) қатыстан жұп және тақ ретті лайықты бөлшектердің өзара орналасуына байланысты маңызды бір салдар шығады. Айталық,
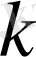 -жұп сан болсын,
-жұп сан болсын,
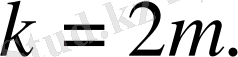 онда (23) қатыстан:
онда (23) қатыстан:
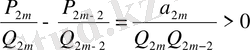
немесе
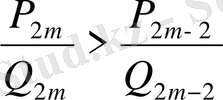
шығады. Мұнда
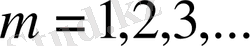 дей отырып, индексі жұп болып келген лайықты бөлшектердің өспелі тізбек құрастыратынын байқаймыз:
дей отырып, индексі жұп болып келген лайықты бөлшектердің өспелі тізбек құрастыратынын байқаймыз:
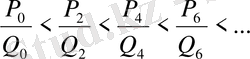 (24)
(24)
Егерде
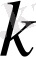 тақ сан болса,
тақ сан болса,
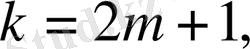 онда (23) -дан
онда (23) -дан
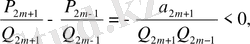
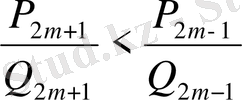 .
.
Мұндағы
 ге
ге
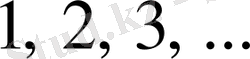 мәндер бере отырып, индекстері тақ сан болып келген лайықты бөлшектер кемімелі тізбек құрастырады деген қорытындыға келеміз:
мәндер бере отырып, индекстері тақ сан болып келген лайықты бөлшектер кемімелі тізбек құрастырады деген қорытындыға келеміз:
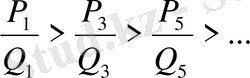 (25)
(25)
Егерде (21) -дегі
 десек,
десек,
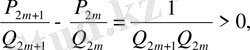
яғни
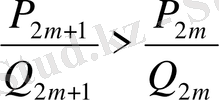
шығады. Сөйтіп, қандай болса да, тақ ретті лайықты бөлшек өзінің алдында тұрған жұп ретті лайықты бөлшектен үлкен болады. мәселен,
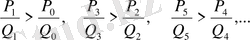 (26)
(26)
(24), (25) және (26) теңсіздіктерден, әрбір тақ ретті лайықты бөлшек (яғни индексі тақ болып келген лайықты бөлшек) жұп ретті лайықты бөлшектердің кез келгенінен үлкен болатындығын шығарып алу оңай.
Сөйтіп,
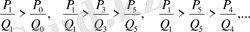
Жасалған қорытындыны мынандай теорема ретінде тұжырымдауға болады:
6-теорема. Жұп ретті лайықты бөлшектер өспелі, ал тақ ретті лайықты бөлшектер кемімелі тізбек құрастырады. Әрбір тақ ретті лайықты бөлшек кез келген жұп ретті лайықты бөлшектен үлкен болады.
шынында, айталық
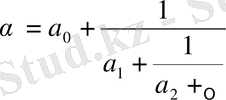
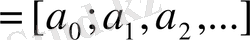
Үздіксіз бөлшегі берілсін. Толық бөліндіні
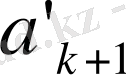 арқылы белгілейік:
арқылы белгілейік:
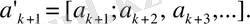
Сонда
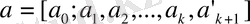 ні
ні
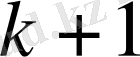 -нөмірлі лайықты бөлшек ретінде қарастыруға болады. демек, 2-теорема бойынша
-нөмірлі лайықты бөлшек ретінде қарастыруға болады. демек, 2-теорема бойынша
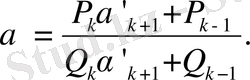 (27)
(27)
Мұндағы
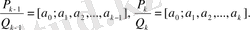
(27) -дан
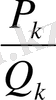 лайықты бөлшегін шегеріп,
лайықты бөлшегін шегеріп,
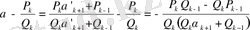
екенін табамыз, немесе (21) -ге сүйенсек
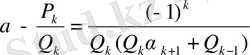 (28)
(28)
шығады.
Егер
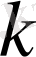 жұп сан болса,
жұп сан болса,
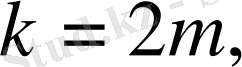 онда (28) -ден, кез келген
онда (28) -ден, кез келген
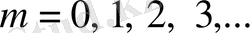 үшін
үшін
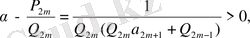 (29)
(29)
аламыз, ал
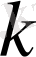 тақ болса,
тақ болса,
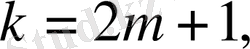 онда
онда
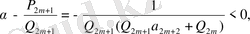 (30)
(30)
(29) мен (30) теңсіздіктері
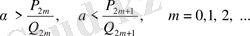
береді, яғни
 үздіксіз бөлшегінің мәні әрбір жұп ретті лайықты бөлшектен артық, бірақ тақ ретті лайықты бөлшектен кем болады.
үздіксіз бөлшегінің мәні әрбір жұп ретті лайықты бөлшектен артық, бірақ тақ ретті лайықты бөлшектен кем болады.
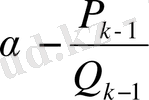 айырмасын табайық. Ол үшін
айырмасын табайық. Ол үшін
 нің (27) -дағы мәнін пайдаланайық. Сонда
нің (27) -дағы мәнін пайдаланайық. Сонда
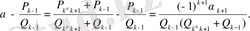 (31)
(31)
Егерде

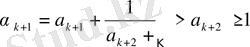
екенін ескерсек, (28) мен (31) теңдіктерінен
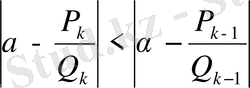 (32)
(32)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz