Графтар теориясы, торлық есептердің экономикалық қойылымы және графтағы ең кіші ара қашықтықты анықтау бағдарламасы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:
МАЗМҰНЫ
КІРІСПЕ . . . 3
I. ГРАФТАР ТУРАЛЫ НЕГІЗГІ МӘЛІМЕТТЕР . . . 7
1. 1. Тарихи анықтама . . . 7
1. 2. Графтар теориясының негізгі терминдері және теоремалары . . . 14
1. 3. Графтағы әртүрлі есептердің сипаты . . . 20
II. ТОРЛЫҚ ЕСЕПТІҢ ЭКОНОМИКАЛЫҚ ҚОЙЫЛУЫ . . . 21
2. 1. Есептің торлық ұсынылуы және торлық модельдерді құру ережелері . . . 21
2. 2. Ең кіші жолды табу . . . 24
2. 3. Бір торлық есепті шешу үшін динамимкалық программалау әдісі . . . 27
2. 4. Рационалды тасымалдап - жинақтау маршруттарын анықтау алгоритмі . . . 36
III. Графтағы ең кіші ара қашықтықты анықтау программасы . . . 48
3. 1. Торлық транспорттық есептің қойылымы . . . 48
3. 2. Әдістің және есептеу алгоритмінің сипаты . . . 49
3. 2. 1. Бірінші кезең: Ара қашықтықтың алғашқы кестесін құру . . . 50
3. 2. 2. Екінші кезең:
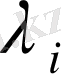 и
и
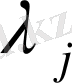 анықтау
. . . 50
анықтау
. . . 50
3. 2. 3. Үшінші кезең: Ең кіші жолдың ұзындығын табу . . . 50
3. 2. 4. Төртінші кезең: Ең кіші жолды табу . . . 50
ҚОРЫТЫНДЫ . . . 52
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . . . . 54
ҚОСЫМША 1 Жаттығулар
ҚОСЫМША 2 Ең кіші ара қашықтықты табу туралы есептің программасы
КІРІСПЕ
Дискреттік программалау - ол ақырлы жиындар мен бүтін сандық торларда экстремальдық есептерді зерттейтін математикалық программалаудың бір бөлімі. Математиканың өз ішінді дискреттік программалау мәселесі, оны «дискреттік және бүтін сандық» математикамен (сандар теориясы, дискреттік талдау, математикалық логика, графтар теориясы, комбинаторлық талдау) жақындастыра түседі [1 - 3] .
Экономиканың, басқарудың, жоспарлаудың және әскери істердің көптеген есептері дискреттік программалау терминдері арқылы тұжырымдалады. Мысалы: өнеркәсіпті орналастыру мен мамандандыру есебі, ауылшаруашылық есептері және тағы басқалар.
Дискреттілік және бүтін сандық сонымен қатар логикалық шарттары бар есептерде де пайда болады.
Дискреттілік пен бүтін сандықтың тиімдестіру есептерінде пайда болуының бірнеше мысалын қарастырайық[3, 4 - 6] :
а) факторлардың физикалық тұрғыдан бөлінбеушілігі: мысалы, 1, 5 домна пешін тұрғызуға немесе 3, 8 ұшақ сатып алуға болмайды. Әдетте бүтін сандық программалау есептері келесі түрде қойылады:
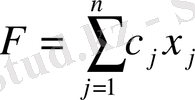 (1)
(1)
функциясының максималды мәнін келесі шарттарды қанағаттандыратындай етіп табу керек.
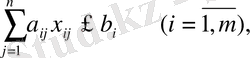 (2)
(2)
 (3)
(3)
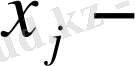 бүтін сандар
бүтін сандар
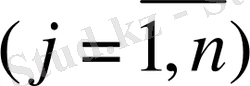 (4)
(4)
б) комбинаторлық есептер (яғни, ақырлы жиындардағы есептер) . Мысалы кезбе саудагер туралы есеп (коммивояжер есебі) . Комбинаторлық есептің тағы бір мысалы, ол көпке белгілі кесте теориясының есебі (күнтізбелік жоспарлау есебі) . Тағы да бір өте қажетті мысал:
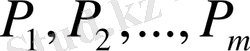 әртүрлі
әртүрлі
 өнім өндіретін
өнім өндіретін
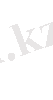
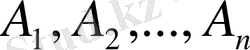 кәсіпорынның мамандануының қарапайым есебін қарастырайық. Әрбір өнімнен сәйкесінше
кәсіпорынның мамандануының қарапайым есебін қарастырайық. Әрбір өнімнен сәйкесінше
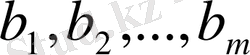 - нен кем емес өнім өндіру керек. Әрбір
- нен кем емес өнім өндіру керек. Әрбір
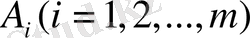 кәсіпорын
кәсіпорын
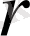 өнім өндіруге арналған және
өнім өндіруге арналған және
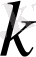 - өнімнің
- өнімнің
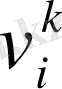 нұсқасы
нұсқасы
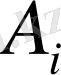 кәсіпорын үшін өндірудің келесі көрсеткіштерімен сипатталады: барлық
кәсіпорын үшін өндірудің келесі көрсеткіштерімен сипатталады: барлық
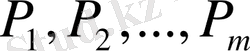 өнім түрлерінен сәйкесінше
өнім түрлерінен сәйкесінше
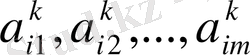 мөлшерде; келтірілген шығындар
мөлшерде; келтірілген шығындар
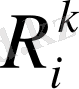 .
.
Шығын көлемі ең аз болатындай етіп, барлық өнім түрлерінің қажеттіліктерін қанағаттандыру керек.
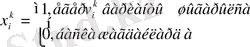
айнымалысын енгізе отырып, математикалық моделін жазамыз.
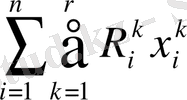 (5)
(5)
функциясын
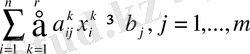 (6)
(6)
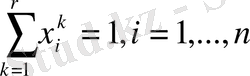 (7)
(7)
 (8)
(8)
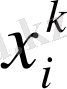 - бүтін сандар,
- бүтін сандар,
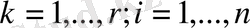 (9)
(9)
шарттарын қанағаттандыра отырып минимизациялау керек.
Дискреттік программалау есептерін шешу барысында бірқатар қысқартылған тәсілдер қолданылуы мүмкін:
1) (1) - (4) бүтін сызықтық программалау есебінің орнына, оған сәйкес келетін (1) - (3) сызықтық программалау есебін шешу керек;
2) толық алмастыру;
3) (1) - (4) бүтін сызықтық прогаммалау есебінің орнына, оған сәйкес келетін (1) - (3) сызықтық программалау есебінің шешімін өзіне жақын болатын бүтін санға «жуықтау» арқылы шешу керек.
Бірінші тәсіл шешімнің бүтіндігіне кепілдік бермейді. Екінші тәсіл өлшемі үлкен есептер үшін өте қиын. Үшінші тәсіл дәл шешімнен ауытқып қана қоймай, сонымен бірге мүмкін болатын шешімдер жиынынан шығып кетуі мүмкін.
Сонда да осы қысқартылған тәсілдер дискреттік программалау есептерін шешудің қима, комбинаторлық, жуық әдістерінің негізін қалайды.
Дискреттік программалаудың пайда болуын, қима әдісінің негізін ұсынған Данцигтің, Фалкерсонның және Джонсонның еңбектерімен байланыстырады. Бірақ, дискреттік программалаудың нағыз дамуы, қима әдісінің алгоритмін алғаш рет ұсынған Гоморидің еңбегінен кейін басталды. Дискреттік программалауға Ю. Финкельштейннің бүтін бір монографиясы арналды.
Торлық әдістің пайда болуына дейін программаның күнтізбелік жоспарлануы іске асырылды. Осындай жоспарлаудың көпке белгілі құралы, уақыттың көлденең шкаласында әрбір амалдың басы және соңының уақытын беретін сызықтық график Ганта. Қазіргі заманғы программалардың күрделілігінің жоғарылауына байланысты программаны іске асырудың барлық процесін тиімділеуді қамтамасыз ететін, жоспарлаудың ең айқын және тиімді әдістерін өңдеу қажет етілді. Сонымен қатар тиімділік қорларды қолданудың экономикалық факторларының есебі мен программаның ұзақтығының минимизациясы түрінде түсіндіріледі.
Программалармен ұйымдық басқару екі аналитикалық әдіс, құрылымдық және күнтізбелік жоспарлауды өңдеу арқасында теориялық және қолданбалы зерттеудің жаңа аймағы болды. Бұл әдістер 1956 - 1958 жылдары ең кіші ара қашықтық есебімен зерттелген.
Графтар теориясы математика пәні ретінде Эйлермен оның Кенигсберг көпірі туралы әйгілі талқылауында салынды. Бірақ Эйлердің бұл мақаласы 1736 жылы жүз жылдың ішінде жалғыз болды. Графтар теориясының мәселесіне қызығушылық өткен жүз жылдың ортасында жандандырылды және Англияда топталды. Графтар теориясының бұлай жандандырылыуы үшін көптеген себептер болды. Электр тізбегін, кристалдар моделін, молекулалар құрылымын зерттеудің арқасында жаратылыс ғылымдары өз әсерлерін тигізді. Формальды ойлаудың дамуы графтар теориясында бинарлық қатынасты үйренуге әкелді. Осы есептердің ішіндегі ең атақтысы - 1850 жылы математиктердің алдында Де Морганмен қойылған төрт бояу мәселесі. Графтар теориясы облысында ешқандай мәселе көп және күрделі жұмыстар тудырған жоқ.
Осы жүз жылдың соңғы оныншы - жиырмасыншы жылдарында қарқынды жоспардағы жаңа дәуіріне енген графтар теориясының ауытқымай дамуының куәгері болды. Бұл программалау, хабарламаларды жіберу теориясы, электр желісі және түйіскен тізбектер, сонымен қатар психология және биология мәселелерін қамтиды.
Бұл дипломдық жұмыс үш тараудан тұрады: 1) Графтар туралы негізгі мәліметтер; 2) Торлық есептің экономикалық қойылым; 3) Графтағы ең кіші ара қашықтықты анықтау программасы. Бірінші тарауда: тарихи анықтамалар, графтар теориясының негізгі терминдері және теоремалары; Екінші тарауда: Есептің торлық ұсынылуы және торлық модельдерді құру ережелері, ең кіші жолды табу, бір торлық есепті шешу үшін динамимкалық программалау әдісі, рационалды тасымалдап - жинақтау маршруттарын анықтау алгоритмі, торлық бөлшек - сызықтық транспорттық есептерді шешу алгоритмдері, транспорттық есеп; Үшінші тарауда: торлық транспорттық есептің қойылымы, әдістің және есептеу алгоритмінің сипаты, бірінші кезең: ара қашықтықтың алғашқы кестесін құру, екінші кезең:
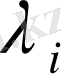 и
и
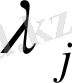 анықтау, үшінші кезең: ең кіші жолдың ұзындығын табу, төртінші кезең: ең кіші жолды табу қарастырылады.
анықтау, үшінші кезең: ең кіші жолдың ұзындығын табу, төртінші кезең: ең кіші жолды табу қарастырылады.
I. ГРАФТАР ТУРАЛЫ НЕГІЗГІ МӘЛІМЕТТЕР
1. 1. Тарихи анықтама
Графтар теориясы - бұл ерекшелігі объектілерді зерттеуге геометриялық жақындау болатын дискреттік математика облысы. Графтар теориясы қазір өркендеуде. Әдетте оны топологияға жатқызады, бірақ ол жиындар теориясының, комбинаторлық математиканың, алгебраның, геометрияның, матрицалар теориясының, ойындар теориясының, математикалық логика және математика пәнінен басқа да көптеген бөлімдерімен қиылысады[1] .
Төбелері мен оларды қосып тұрған доғалар жиынын граф деп атайды. Бағытталған доғалары бар графтарды тор деп атайды.
Графтар теориясының алғашқы есептері математикалық ойын - сауық есептердің шешуімен байланысты. Графтар теориясының алғашқы нәтижелерінің бірі Кенигсберг көпірі туралы есепті шешу кезінде Л. Эйлермен алынған қайталаусыз графтың барлық қабырғаларын тексеріп шығудың болу критерилері болды. 1736 жылы 13 наурыздағы Эйлердің хатынан үзінді: “Маған Кенигсберг қаласында орналасқан арал туралы есеп ұсынылды, одан жеті көпір өтеді. Бір адамның әрбір көпірден бір рет өтіп, үздіксіз олардың барлығынан өту мүмкіндігі сұралады. Дәл осы жерде маған оны әлі ешкім жасай алмағандығы хабарланды, бірақ ешкім дәлелдеген жоқ, бұл мүмкін емес. Бұл сұрақ түсініксіз болса да, маған оны шешу үшін геометрия, алгебра, комбинаторлық өнер қажет емес болғанымен назар аударуды қажет ететін болып көрінді. Көп ойланғаннан кейін мен дәлелденген дәлелдемеге негізделген жеңіл ережені таптым, оның көмегімен осындай барлық есептерде кез келген сан арқылы және қалай болса солай орналасқан көпірлер арқылы айналып шығу мүмкін бе немесе жоқ па екендігін анықтайды”. Кенигсберг көпірлерін схема түрінде былай бейнелеуге болады:
Эйлер ережесі
1. Тақ дәрежелі төбесі жоқ графта графтың кез келген төбесінен басталатын барлық қырларды аралап шығу болады.
2. Тек қана екі тақ дәрежелі төбесі бар графта басы тақ дәрежелі төбенің біреуінде және соңы басқада болатын айналып шығу бар.

3. Екіден көп тақ дәрежелі төбесі бар графта айналып шығу болмайды.
Графтарда бойлай саяхатпен байланысты тағы бір есеп бар. Әрбір төбеден бір рет өтетін жолды іздеу қажет етілетін есептер туралы айтылады. Әрбір төбеден тек қана бір рет өтетін цикл гомильтонды сызық деп аталады. Өкінішке орай, берілген граф гомильтонды екендігін анықтауға болатын және егер болса, онда осындағы барлық гомильтонды сызықтарды табуға болатын жалпы критерий табылмаған.
XIX ғасырдың ортасында тұжырымдалған төрт бояу мәселесі ойын - сауық есебі сияқты, бірақ оны шешу үшін әрекет теориялық және қолданбалы мәндері бар кейбір графтарды зерттеуге әкелді. Төрт бояу мәселесі былай тұжырымдалады: “Кез келген картаның облысын кез келген екі көршілес облыстары әртүрлі түстерге боялатындай төрт түспен бояуға бола ма?”Жауап мақұлданғаны туралы болжам XIX ғасырдың ортасында тұжырымдалды. 1890 жылы әлсіз тұжырым дәлелденді, кез келген жазық карта бес түске боялады. Кез келген жазық картаға оған екі еселенген жазық графты салыстырып, графтар терминінде эквивалентті тұжырымды алады: кез келген жазық графтың хроматикалық кіші екендігі дұрыс па әлде төртке тең бе? Есепті шешудің көптеген әркеттері графтар теориясына бағытталған қатардың дамуына әсерін тигізді. 1976 жылы дербес компьютердің қолданылуымен есептің оң шешімі табылды.
1917 жылы Генри Э. Дьюдени оған мынандай тұжырым берді. Суретте бейнеленген әрбір үш үйден газ, жарық және суды өткізу қажет.
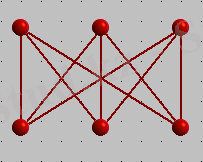
жарық су газ
Қатынастарды бір - бірімен қиылыспай, әрбір үйді электр, газ және суды қайнар көздерімен қосылуы үшін осылай қоюға бола ма? Басқаша айтқанда көрсетілген алты нүктеде төбелері бар жазық граф құруға бола ма? Мұндай графты құруға болмайды екен. Бұл туралы Куратов теоремасы деп аталатын - маңызды теоремалардың бірінде айтылады. Теорема жазық емес әрбір граф екі қарапайым кеңістіктік графтардың біреуінің ішкі графы ретінде мазмұндалатындығын тұжырымдайды:
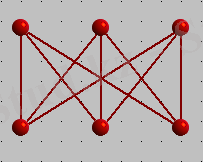
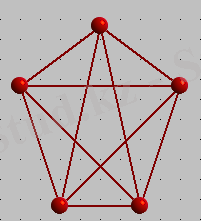
XIX ғасырда практикалық есептерді шешу кезінде графтар теориясына қатысты нәтижелер алынатын жұмыстар пайда болды. Мысалы, Г. Кинхгоф токтар және электрлік схемада қуат үшін теңдеудің толық жүйесін құру кезінде графтардың осындай схемасын ұсынуды және осы графта қалған ағаштарды табу ұсынылды. А. Кэли шекті көмірсутектердің изомерлерінің санын санау есебінен шығып, берілген қасиеттермен басқаратын ағаштарды сипаттау және санау есептеріне келді және олардың кейбіреулерін шешті.
XX ғасырда графтарға байланысты есептер физикаға, химияға, биологияның электротехникасына, экономикаға, социологияға ғана емес және математиканың ішінде топология, алгебра, ықтималдықтар теориясы, сандар теориясы сияқты бөлімдерінде пайда бола бастады. XX ғасырдың басында графтар кейбір математикалық объектілерді ұсыну және әртүрлі дискретті есептердің формальды қойылуы үшін қолданыла бастады; сонымен қатар “граф” терминдер қатарында басқа терминдер қолданылады, мысалы, карта, комплекс, диаграмма, тор, лабиринт. Д. Кениг монографиясы 1936 жылы жарыққа шыққаннан кейін “граф” термині басқаларға қарағанда ең көп қолданылатын болды. Бұл жұмыста сол уақытта әйгілі фактілер жүйелендірілді. 1936 жылы Ойстен Ордың графтар теориясына элементар кіріспесі мазмұндалатын кішкене кітапшасы шықты. 1962 жылы Англияда француз математигі Клод Бердждың “Графтар теориясы және оның қосымшасы” кітабы шықты. Екі кітап та математикамен шұғылданатын жанкүйерлер үшін назар аудартады.
XX ғасырдың жиырмасыншы - отызыншы жылдарында графтар теориясына жаңа бағыттың қатарының қалыптасуына әкелген, графтардың симметриясына, жоспарлануға, байланыс қасиеттерін үйренуге қатысты алғашқы нәтижелер пайда болды.
Қырықыншы жылдардың аяғы елуінші жылдардың басында графтар теориясы бойынша зерттеулер едәуір кең таралды, алдымен есептеу техникасы және кибернетика дамыды. Есептеу техникасының дамуының, күрделі кибернетикалық жүйелерді үйренудің арқасында графтар теориясына назар аударылды, графтар теориясының мәселесі маңызды образбен толықтырылды. Сонымен қатар дербес компьютерді қолданумен шешімге берілмеген есептеудің көп мөлшерімен байланысты практикада болатын нақты есептерді шешуге мүмкіндік берді. Графтар теориясының экстермальды есептерінің қатары үшін оларды шешу әдістері өңделді, мысалы, осындай әдістердің біреуі тор арқылы максимал ағынды құру туралы есепті шешуге мүмкіндік береді. Бұрын зерттелген графтардың жеке кластары үшін кейбір есептердің графтар үшін шешімі жуықталған графтарға қарағанда осы кластардан оңай табылады.
Графтар теориясының мәселесін сипаттап, кейбір бағыттар комбинаторлық сипат, басқалары - геометриялық сипат таситындығын ерекшелеуге болады. Біріншіге мыналар жатады, мысалы, тағайындалған қасиеттерімен графтарда атап өту және санау есептері, қасиеттері берілген графтарды салу туралы есептер. Геометриялық сипат графтар теориясы есептерінің көптеген циклдарын тасиды, мысалы, айналып шығу графтары, қалау графтары. Графтардың әртүрлі классификациясымен байланысты бағыттар бар, мысалы, оларды жіктеу қасиеті бойынша.
Қасиеті тағайындалған графтардың болуы туралы нәтиженің мысалы, кейбір графтардың төбелерінің деңгейлермен жүзеге асу критериінің саны: қосындысы жұп болатын
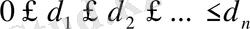 бүтін сандар жиыны, графтың төбелерін деңгейлермен қысқа қыр және тұзақсыз жүзеге асыруға болады, егер кез келген
бүтін сандар жиыны, графтың төбелерін деңгейлермен қысқа қыр және тұзақсыз жүзеге асыруға болады, егер кез келген
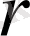 үшін
үшін
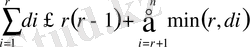 шарты орындалса.
шарты орындалса.
Қасиеттері берілген графтарды санау туралы есептің мысалы қырлар және төбелерінің саны бірдей изоморфты емес графтардың санын табу туралы есеп болады.
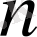 төбелері бар изоморфты емес ағаштардың саны үшін асимтотты формула алынды
төбелері бар изоморфты емес ағаштардың саны үшін асимтотты формула алынды
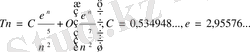
Тұзақсыз изоморфты емес графтардың
 саны және
саны және
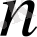 төбесі бар еселі
төбесі бар еселі
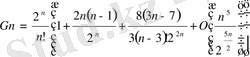
қырлар үшін көрсетілді.
Жалпы сипатты таситын мәселелердің қатарында графтар теориясында есептің арнайы циклдары бар. Олардың біреуінде графтардың байланыстылығының әртүрлі қасиеттері зерттеледі, байланыстың қасиеттері бойынша графтарды салу зерттеледі. Байланыс желісінің, электрлі схеманың, коммуникациялық тордың сенімділігін талдау кезінде графтың әртүрлі төбелерін біріктіретін, қиылыспайтын тізбектер санын табу туралы есептер пайда болды. Мұнда нәтижелер қатары алынған. Мысалы, графтың екі аралас емес төбелерін бөліп тұратын төбелердің ең аз саны осы жұбын біріктіретін қиылысатын қарапайым тізбектердің ең үлкен санына тең. Графты байланыстыратын шамаларды орнатудың тиімді алгоритмдері құрылды және критериі табылды.
Басқа бағыттағы графтар теориясын зерттеуде графтың қырлары немесе барлық төбелері бар маршруттар оқытылады: барлық қырлары бар және әрбір қырдан бір рет өтетін байланысқан графта цикл болады, графтың барлық төбелерінің жұп деңгейлері болғанда. Графтың төбелер жиынын аралап шығу жағдайында графтың барлық төбелерінен бір рет өтетін циклдың болуының тек қана жеткілікті шартының қатары болады. Графты бояумен байланысты анықталған қасиеті бар, (қыр) төбелер жиынының бөлшектенуі оқытылатын, мысалы, аралас төбелер (қыр) әртүрлі жиындарға жатуы керек есептердің циклы графтар теориясының арнайы сипаттамалық бағыты болады. Түстердің ең аз саны максимал деңгейлі
 кез келген тұзақсыз графтың қырларын бояу үшін жеткілікті
кез келген тұзақсыз графтың қырларын бояу үшін жеткілікті
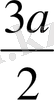 тең, ал кез келген тұзақсыз графтың төбесін және еселі қырларын бояу үшін
тең, ал кез келген тұзақсыз графтың төбесін және еселі қырларын бояу үшін
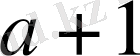 түс жеткілікті.
түс жеткілікті.
Есептің басқа да циклдары бар, олардың кейбіреулері математиканың әртүрлі бөлімдерінің әсерімен қосылды. Топологияның әсерімен әртүрлі кеңістікте графтарды енгізу өңделеді. Мысалы, жазықтықта графты енгізудің қажетті және жеткілікті шарты алынды: граф жазық болады, егер ол бес төбелі графтан қырларды бөлу көмегімен алынатын графтардан тұрса. Алгебраның әсерімен графтардың автоморфизмдерінің топтары оқытылды. Әрбір соңғы топ кейбір графтың автоморфты тобына изоморфты екендігі дәлелденді. Ықтималдықтар теориясының әсері кездейсоқ графтарды зерттеуде айтылды. Көптеген қасиеттер “барлық” графтар үшін оқытылды; мысалы, барлық графтар
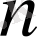 төбелермен байланысқан, диаметрі екі, гамильтонды циклға ие болатындығы көрсетілді.
төбелермен байланысқан, диаметрі екі, гамильтонды циклға ие болатындығы көрсетілді.
Графтар теориясында экстремальды есептерді шешудің арнайы әдістері бар. Олардың біреуі
 төбесінен
төбесінен
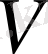 төбесіне тор арқылы өткізуге болатын максимал ағын
төбесіне тор арқылы өткізуге болатын максимал ағын
 және
және
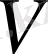 төбелерін бөлетін қималардың минимал өту қабілеттілігіне тең екендігін тұжырымдайтын, минимал қима және максималды ағын туралы теоремаға негізделген. Максимал ағынды табудың әртүрлі тиімді алгоритмдері құрылған.
төбелерін бөлетін қималардың минимал өту қабілеттілігіне тең екендігін тұжырымдайтын, минимал қима және максималды ағын туралы теоремаға негізделген. Максимал ағынды табудың әртүрлі тиімді алгоритмдері құрылған.
Графтар теориясында алгоритмдік сұрақтар үлкен мәнге ие. Ақырлы графтар үшін, қырлар және төбелердің ақырлы жиын болатын графтар үшін, ереже бойынша, есепті шешудің алгоритмінің бар болу мәселесі, соның ішінде экстремальды, оң шешіледі. Ақырлы графтармен байланысты көптеген есептерді шешудің әртүрлі нұсқаларының толық жиналуының көмегімен орындалуы мүмкін. Бірақ, осындай әдіспен тек қана төбелер және қырларының саны көп емес графтар үшін есепті шешуге болады. Сонымен графтар теориясы үшін маңызды мән нақты және жуық шешімді табатын тиімді алгоритмдерді құрады. Кейбір есептер үшін мұндай алгоритмдер құрылған, мысалы, максимал ағынды табу, изоморфты ағашты анықтау, графтың жоспарлануын орнату үшін.
Графтар теориясының әдістері және нәтижелері тасымалдау туралы транспорттық есепті шешу кезінде, тағайындау туралы есептің тиімді шешімін табу үшін қолданылады. Жоспарлау және жобаны өңдеу кезінде, жүктерді тасудың тиімді маршрутын құру кезінде, сонымен қатар программалауда, әртүрлі дискреттік құралдарды құруда күрделі технологиялық процестерді модельдеу кезінде “тар орындарды” белгілеу үшін қолданылады.
1. 2. Графтар теориясының негізгі терминдері және теоремалары
1. Граф -
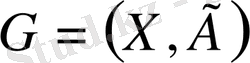 объектілерінің жұбы,
объектілерінің жұбы,
 - ақырлы жиын, ал
- ақырлы жиын, ал
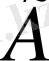 -
-
 тура туындының ақырлы жиыны. Сонымен қатар
тура туындының ақырлы жиыны. Сонымен қатар
 төбелер жиыны деп аталады, ал
төбелер жиыны деп аталады, ал
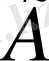 -
-
 графының доғалар жиыны.
графының доғалар жиыны.
2. Нүктелердің кез келген ақырлы жиыны (төбе), олардың бағытталған жұп - жұбымен біріктірілгендерін, граф ретінде қарастыруға болады.
3. Егер
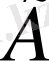 жиынында барлық жұптар реттелген болса, онда мұндай граф бағытталған граф деп аталады.
жиынында барлық жұптар реттелген болса, онда мұндай граф бағытталған граф деп аталады.
4. Доға - бағытталған графтың қыры.
5. Граф азғындалған деп аталады, егер оның қыры болмаса.
6.
 төбесі
төбесі
 қырына инцидентті деп аталады, егер қыр осы төбені төбенің қандай да бір доғасымен біріктірсе.
қырына инцидентті деп аталады, егер қыр осы төбені төбенің қандай да бір доғасымен біріктірсе.
7.
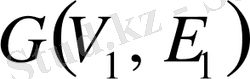 графы
графы
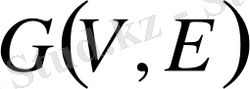 графының ішкі графы деп
графының ішкі графы деп
 төбелер жиыны және
төбелер жиыны және
 қырлар (доға) жиыны бар графтар аталады,
қырлар (доға) жиыны бар графтар аталады,
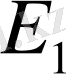 - дің әрбір қыры(доға)
- дің әрбір қыры(доға)
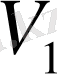 - дің төбелеріне инцидентті. Басқаша айтқанда ішкі графтар алғашқы графтың кейбір төбелерінен және қырларынан тұрады.
- дің төбелеріне инцидентті. Басқаша айтқанда ішкі графтар алғашқы графтың кейбір төбелерінен және қырларынан тұрады.
8. Екі соңғы
 - ға жататын, тек қана сол қырлары бар, төбелер жиыны
- ға жататын, тек қана сол қырлары бар, төбелер жиыны
 болатын ішкі граф
болатын ішкі граф
 төбелер жиынымен туындаған, ішкі граф деп аталады.
төбелер жиынымен туындаған, ішкі граф деп аталады.
9. Ішкі граф қалдық ішкі граф деп аталады, егер оның төбелер жиыны графтың төбелер жиынына сәйкес келсе.
10. Төбелер аралас деп аталады, егер оларды біріктіретін қырлар бар болса.
11.
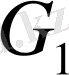 және
және
 екі қыр аралас деп аталады, егер бір мезгілде
екі қыр аралас деп аталады, егер бір мезгілде
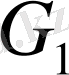 және
және
 инцидентті төбе бар болса.
инцидентті төбе бар болса.
12. Әрбір графты қырларға сәйкес келетін сызықтармен біріктірілген, төбелерге сәйкес келетін нүктелер жиынының кеңістігінде ұсынуға болады - мұндай ұсыну графтың тегістелуі деп аталады.
13. Үш өлшемді кеңістікте кез келген графты тегістеу ретінде ұсынуға болатындығы дәлелденді, сонымен, қырларға сәйкес келетін сызықтар ішкі нүктелерде қиылыспайды. Екі өлшемді кеңістік үшін бұл мүлдем дұрыс емес. Екі өлшемді кеңістікте тегістеу ретінде ұсынуға болатын графтар жазық деп аталады. Басқаша айтқанда, қырлары қиылыспайтын болып жазықтықта бейнеленуі мүмкін граф жоспарланған деп аталады.
14. Графтың қырларымен шектелген жазықтық кейбір жазықтықта бейнеленген графтың жағы деп аталады.
Берілген жақ ұғымы, маңызы бойынша, көпжақты жақ ұғымына сәйкес келеді. Бұл жағдайда жазықтық ретінде көпжақтың жазықтығы шығады. Егер көпжақ дөңес болса, барлық жақтарды сақтап, оны жазықтықта бейнелеуге болады. Бұны келесі әдіспен ұсынуға болады: көпжақтың бір жағын созамыз, ал көпжақтың өзін осы жақтың ішінде толық орналасатындай жіңішкелейміз. Нәтижесінде жазық граф аламыз. Біз созған жақ “жоғалады”, бірақ оған графты шектейтін, жазықтықтың бөліктерінен тұратын жақ сәйкес келеді.
Сонымен, төбелер қырлар және көпжақтың жақтары туралы айтуға болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz