Дирихле сипаттары мен L-функциялары арқылы арифметикалық прогрессиядағы жай сандардың таралуы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:
Мазмұны
Кіріспе . . .
I-тарау. Дирехле функциясының негізгі қасиеттері . . .
§ 1. 1. Сипаттар және олардың қасиеттері . . .
§ 1. 2. Дирехле функциясы, оның қасиеттері . . .
§ 1. 3. функциясының нөлге айналмауы . . .
§ 1. 4. функциясының нөлдері туралы . . .
II-тарау. Арифметикалық прогрессиядағы жай сандар
§ 2. 1. Прогрессиядағы жай саны туралы . . .
§ 2. 2. Жай сандар санын есептеудегі Дирехле функциясымен байланысы . . .
§ 2. 3. Асимптотикалық формулалар . . .
Қорытынды . . .
Пайдаланылған әдебиеттер тізімі . . .
Кіріспе
Дипломдық жұмыстың тақырыбы - жай сандардың арифметикалық прогрессияда таралуы.
Жай сандар деп тек бірге және өзіңе бөлінетін оң бүтін сандарды атаймыз.
Арифметикалық прогрессия - дегеніміз натурал қатардың шектеусіз ең бір қарапайым бөлімше тізбегі.
Берілген жұмыстың негізгі мақсаты жай сандардың арифметикалық ппогрессияда таралуын оқып - зерттеу болып табылады. Математика ғылымына жай сандар туралы ұғым қашан енгені тарихта белгісіз.
Менің дипломдық жұмысым екі тараудан тұрады: Дирехле функциясының негізгі қасиеттері және арифметикалық прогрессиядағы жай сандар.
Бірінші тарау төрт бөлімнен тұрады. Онда сипаттар және олардың қасиеттері, Дирехле функциясы және оның қасиеттері, Дирехле функциясының нөлдері туралы қарастырылды.
Дипломдық жұмыстың екінші тарауы үш бөлімнен тұрады. Екінші тарауда прогрессиядағы жай сандар саны туралы, жай сандар санын есептеудегі Дирехле функциясымен байланысы және асимптотикалық формулалар қарастырылатын болатын.
1837 жылы Дирехле арифметикалық прогрессияда шексіз көп жай сандар бар болатындығын дәлелдеген.
Қорытынды бөлімде дипломдық жұмысқа қысқаша шолу жасалған. Соңында әдебиеттер тізімі келтірілген.
I-тарау. Дирехле функциясының негізгі қасиеттері.
§ 1. 1. Сипаттар және олардың түрлері.
Айталық,
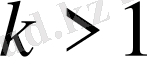 бүтін саны болсын. Сонымен қатар
бүтін саны болсын. Сонымен қатар
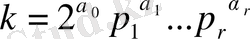 (1. 1. 1)
(1. 1. 1)
қарапайым көбейіткіштерге жіктелсін. Мульдері бойынша
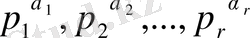 сандарының алғашқы түбірлерін
сандарының алғашқы түбірлерін
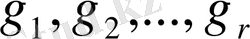 арқылы белгілейміз. Онда әрбір
арқылы белгілейміз. Онда әрбір
 натурал саны үшін
натурал саны үшін
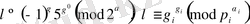
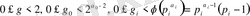 ,
,
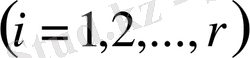 (1. 1. 2)
(1. 1. 2)
болатындай
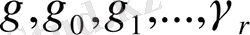 сандары табылады және әрбір
сандары табылады және әрбір
 үшін
үшін
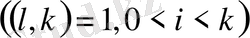
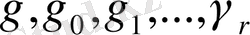 түріндегі бір ғана жүйе табылады. Айталық,
түріндегі бір ғана жүйе табылады. Айталық,
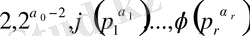 реттінің кез келген бірлік түбірлері
реттінің кез келген бірлік түбірлері
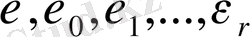 болсын.
болсын.
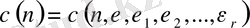 функциясын мына формула арқылы анықтаймыз
функциясын мына формула арқылы анықтаймыз
 (1. 1. 3)
(1. 1. 3)
Мұнда
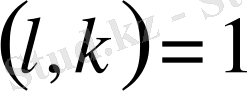 үшін
үшін
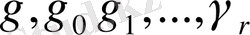 (1. 1. 2) формуласымен анықталады. Егер
(1. 1. 2) формуласымен анықталады. Егер
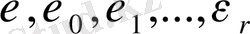 барлық мүмкіншілік тәсілдерімен таңдалған болса, онда біз
барлық мүмкіншілік тәсілдерімен таңдалған болса, онда біз
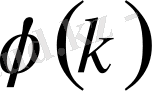 жиынтығында функцияларды анықтаймыз. Барлық натурал сандар жиынында анықталған бұл функциялар
жиынтығында функцияларды анықтаймыз. Барлық натурал сандар жиынында анықталған бұл функциялар
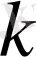 модулі бойынша сипат деп аталады. Дербес жағдайда,
модулі бойынша сипат деп аталады. Дербес жағдайда,
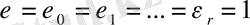 болса, онда сипатты бас сипат деп атап, былай белгілейміз:
болса, онда сипатты бас сипат деп атап, былай белгілейміз:
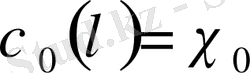 . Сонымен қатар
. Сонымен қатар
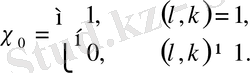 (1. 1. 4)
(1. 1. 4)
Әрбір сипат үшін
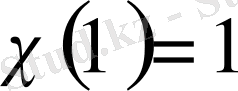 болады.
болады.
Мысалы.
 болғанда,
болғанда,
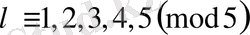 үшін
үшін
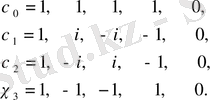
мәндеріне ие болатын төрт сипат табылады.
Кез келген
 және
және
 натурал сандары үшін келесі теңдіктерді алуға болады:
натурал сандары үшін келесі теңдіктерді алуға болады:
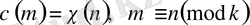 (1. 1. 5)
(1. 1. 5)
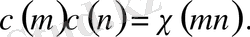 (1. 1. 6)
(1. 1. 6)
Сипаттардың негізгі қасиеті мына формулалар арқылы өрнектеледі
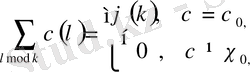 (1. 1. 7)
(1. 1. 7)
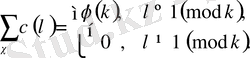 (1. 1. 8)
(1. 1. 8)
Сонымен бірге
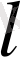 (1. 1. 7) формулада
(1. 1. 7) формулада
 бойынша толық қалыңдылар жүйесін жүріп өтеді, ал
бойынша толық қалыңдылар жүйесін жүріп өтеді, ал
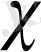 (1. 1. 8) формуласында
(1. 1. 8) формуласында
 бойынша барлық
бойынша барлық
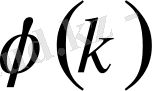 сипатымен жүріп өтеді. (1. 1. 7) формуласын дәлелдеу үшін
сипатымен жүріп өтеді. (1. 1. 7) формуласын дәлелдеу үшін
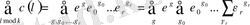 (1. 1. 9)
(1. 1. 9)
арақатынасын алайық. Мұнда
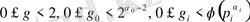 . Егер
. Егер
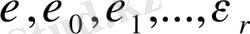 сандарының біреуі бірге тең болмаса, яғни егер
сандарының біреуі бірге тең болмаса, яғни егер
 бас сипат болмаса, онда әр
бас сипат болмаса, онда әр
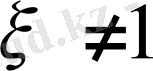 бірлігіне тиісті
бірлігіне тиісті
 дәрежелі түбірлері үшін сәйкес қосынды нөлге тең болады
дәрежелі түбірлері үшін сәйкес қосынды нөлге тең болады
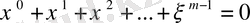 .
.
(1. 1. 9) қосындысы үшін
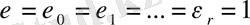 болғанда
болғанда
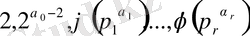 мәндерін аламыз. Осымен (1. 1. 7) формуласы дәлелденеді.
мәндерін аламыз. Осымен (1. 1. 7) формуласы дәлелденеді.
Енді (2. 8) формуласын дәлелдейік. Ол үшін
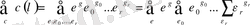 (1. 1. 10)
(1. 1. 10)
қосындысын алайық. Мұндағы қосынды сәйкес
 бірліктердің барлық түбірлері
бірліктердің барлық түбірлері
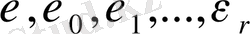 бойынша
бойынша
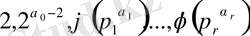 реттің күнделікті
реттің күнделікті
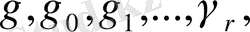 жүйесінде қарастыралады. Егер
жүйесінде қарастыралады. Егер
 сандарының біреуі нөлге тең болмаса, яғни
сандарының біреуі нөлге тең болмаса, яғни
 және егер
және егер
 бірліктерге тиісті барлық
бірліктерге тиісті барлық
 дәреже түбіріне жүріп өтетін болса, онда сәйкес қосынды нөлге ұмтылады
дәреже түбіріне жүріп өтетін болса, онда сәйкес қосынды нөлге ұмтылады
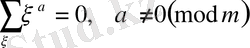 .
.
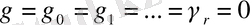 үшін (1. 1. 10) қосынды мәні
үшін (1. 1. 10) қосынды мәні
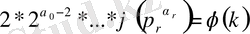 болады, бұдан (1. 1. 8) формуласы дәлелденеді.
болады, бұдан (1. 1. 8) формуласы дәлелденеді.
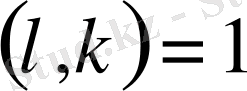 болғанда (1. 1. 8) формуласынан шығады
болғанда (1. 1. 8) формуласынан шығады
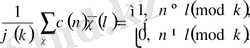 (1. 1. 11)
(1. 1. 11)
Әрбір
 сипаты үшін
сипаты үшін
 функциясы
функциясы
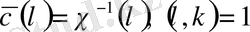 (1. 1. 12)
(1. 1. 12)
формуласымен анықталады. Мұнда
 үшін
үшін
 мәнінде барлық бірлік түбірлерлердің көбейтіндісі бар. Айталық,
мәнінде барлық бірлік түбірлерлердің көбейтіндісі бар. Айталық,
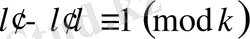 салыстыру есептеуі болсын. Онда
салыстыру есептеуі болсын. Онда
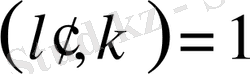 және
және
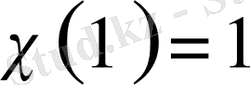 болғанда (1. 1. 5), (1. 1. 6) формулаларынан
болғанда (1. 1. 5), (1. 1. 6) формулаларынан
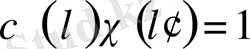 шығатыны анық. Осыдан
шығатыны анық. Осыдан
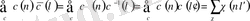
шығады. Келесі салыстырулары
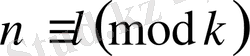 және
және
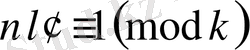 ,
,
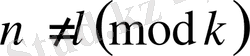 және
және
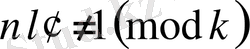 тең мәнді болғандықтан ақырғы арақатынасынан және (1. 1. 8) арақатынасынан (1. 1. 11) шығады.
тең мәнді болғандықтан ақырғы арақатынасынан және (1. 1. 8) арақатынасынан (1. 1. 11) шығады.
Теорема 1. 1. 1.
барлық
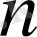 натурал саны үшін анықталған және келесі үш шартты қанағаттандыратын әрбір
натурал саны үшін анықталған және келесі үш шартты қанағаттандыратын әрбір
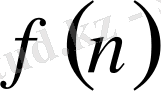 функциясы
функциясы
- ( толық мультипликативті )
қарастырып отырған
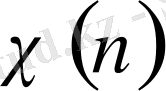 функцияларының біреуі болуы керек.
функцияларының біреуі болуы керек.
Расында да, 3-ші шарттан
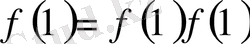 және 1-ші шарттан
және 1-ші шарттан
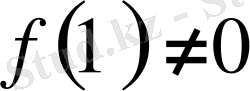 болса, онда
болса, онда
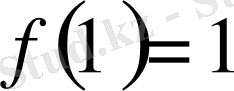 болатыны шығады. (1. 1. 2) формуласын жалпылай
болатыны шығады. (1. 1. 2) формуласын жалпылай
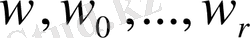 сандары бар болатындығы элементарлық сандар теориясында дәлелденген және кез келген
сандары бар болатындығы элементарлық сандар теориясында дәлелденген және кез келген
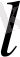 (
(
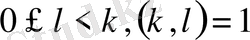 ) санын мына түрде жазуға болады
) санын мына түрде жазуға болады
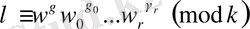 , (1. 1. 13)
, (1. 1. 13)
сонымен бірге
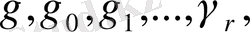 (1. 1. 2) формуласындағы мәнге ие. Және де мына арақатынас орындалады
(1. 1. 2) формуласындағы мәнге ие. Және де мына арақатынас орындалады
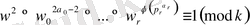 . Бұл арақатынасынан 2-ші және 3-ші шарттарды пайдалана отыра
. Бұл арақатынасынан 2-ші және 3-ші шарттарды пайдалана отыра
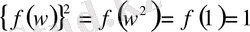 теңдігін аламыз, сондықтан
теңдігін аламыз, сондықтан
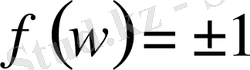 . Осыған ұқсас
. Осыған ұқсас
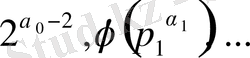 ретінің бірлік түбірлері
ретінің бірлік түбірлері
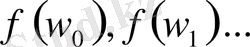 болуы керектігін аламыз. Егер
болуы керектігін аламыз. Егер
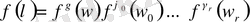 болса, онда
болса, онда
 -сипат екені анық.
-сипат екені анық.
Сондықтан
 бойынша сипатты 1-ші және 2-ші, 3-ші шарттарын қанағаттандыратын функция ретінде анықтауға болады.
бойынша сипатты 1-ші және 2-ші, 3-ші шарттарын қанағаттандыратын функция ретінде анықтауға болады.
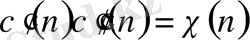 екі сипаттың көбейтіндісі тағы
екі сипаттың көбейтіндісі тағы
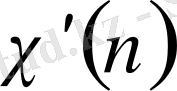 және
және
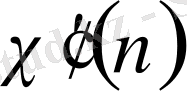 -сипат болатыны анық.
-сипат болатыны анық.
Теорема 1. 1. 2.
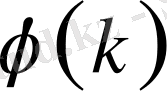 жиынтығында кез келген екі сипат өз ара тең емес, яғни барлық
жиынтығында кез келген екі сипат өз ара тең емес, яғни барлық
 мәнінде сәйкес келмейді.
мәнінде сәйкес келмейді.
Айталық, мысалы, (2. 3) арақатынасында
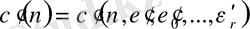 ,
,
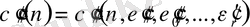 .
.
Онда
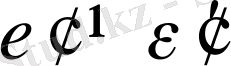 немесе ең болмағанда бір
немесе ең болмағанда бір
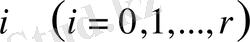 үшін
үшін
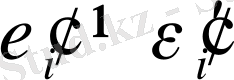 . Егер соңғы жағдай орын алса, онда мынадай
. Егер соңғы жағдай орын алса, онда мынадай
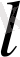 үшін
үшін
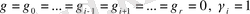
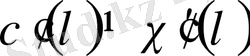 болатыны анық.
болатыны анық.
Егер
 болғанда барлық натурал
болғанда барлық натурал
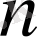 саны үшін жалғыз сипат
саны үшін жалғыз сипат
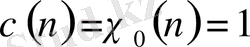 анықталса, онда бұл сипат жоғарыда айтылған барлық сипаттардың қасиеттеріне ие болады.
анықталса, онда бұл сипат жоғарыда айтылған барлық сипаттардың қасиеттеріне ие болады.
Енді эквивалентті және примитивті сипаттарға тоқталайық.
Айталық,
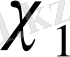 және
және
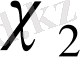 -сәйкес
-сәйкес
 және
және
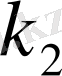 модульдері бойынша екі сипат болсын.
модульдері бойынша екі сипат болсын.
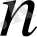 саны үшін
саны үшін
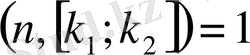 орындалсын. Мұндағы
орындалсын. Мұндағы
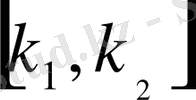 -
-
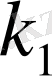 және
және
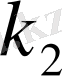 модульдерінің ең кіші бөлгіші. Сонда
модульдерінің ең кіші бөлгіші. Сонда
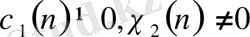 теңдіктеріне ие боламыз.
теңдіктеріне ие боламыз.
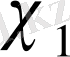 және
және
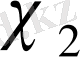 сипаттары эквивалентті деп аталады, егер
сипаттары эквивалентті деп аталады, егер
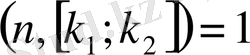 үшін
үшін
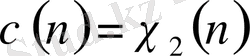 орындалса.
орындалса.
Басқаша айтқанда, егер
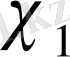 және
және
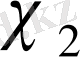 нөлден өзгеше мәнге ие болса. Онда төмендегі теңдіктермен анықталған функция
нөлден өзгеше мәнге ие болса. Онда төмендегі теңдіктермен анықталған функция
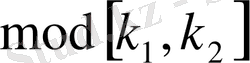 бойынша
бойынша
 сипаты болады
сипаты болады
 (1. 1. 13)
(1. 1. 13)
Мұнда
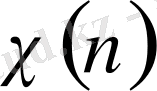 1-ші және 2-ші, 3-ші шарттарын қанағаттандырады. Кейін
1-ші және 2-ші, 3-ші шарттарын қанағаттандырады. Кейін
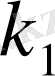 және
және
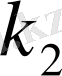 натурал сандары болады. Егер
натурал сандары болады. Егер
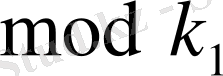 бойынша
бойынша
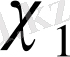 сипатына
сипатына
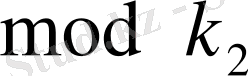 бойынша
бойынша
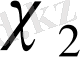 сипаты эквивалентті болса, онда
сипаты эквивалентті болса, онда
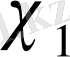 сипатын
сипатын
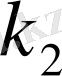 модулі бойынша немесе
модулі бойынша немесе
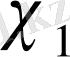 сипатын
сипатын
 бойынша анықтаймыз.
бойынша анықтаймыз.
Лемма 1. 1. 1.
Егер
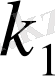 бөлінетін болса, онда кез келген
бөлінетін болса, онда кез келген
 бойынша
бойынша
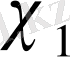 сипаты кез келген модулімен анықталуы мүмкін.
сипаты кез келген модулімен анықталуы мүмкін.
Дәлелдеу.
Айталық,
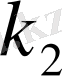 бөлінетін болсын. Онда
бөлінетін болсын. Онда
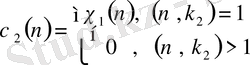
 бойынша
бойынша
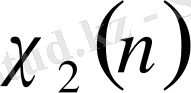 сипаты 1-ші және 2-ші, 3-ші шарттарын қанағаттандырады. Сондықтан
сипаты 1-ші және 2-ші, 3-ші шарттарын қанағаттандырады. Сондықтан
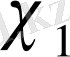 сипаты
сипаты
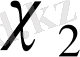 сипатына эквивалентті.
сипатына эквивалентті.
Лемма 1. 1. 2.
Егер
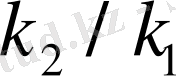 және
және
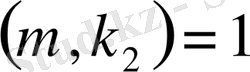 болса, онда
болса, онда
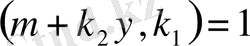 (1. 1. 14)
(1. 1. 14)
сандары табылады.
Дәлелдеу.
Айталық,
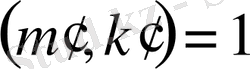 және
және
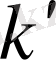
 ді бөлетін, бірақ
ді бөлетін, бірақ
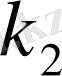 ні бөлмейтін барлық жай сандар көбейтіндісі болсын. Онда
ні бөлмейтін барлық жай сандар көбейтіндісі болсын. Онда

салыстырылуы шешіледі. Егер
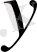 шешім болып табылса, онда
шешім болып табылса, онда
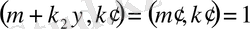
және жорамалдауымыз бойынша
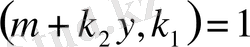 болады.
болады.
Лемма 1. 1. 3.
Айталық,
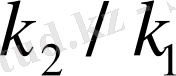 болсын.
болсын.
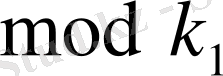 бойынша
бойынша
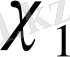 сипаты
сипаты
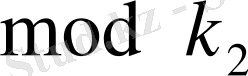 бойынша анықталуы үшін төмендегі шарттың орындалуы қажетті және жеткілікті
бойынша анықталуы үшін төмендегі шарттың орындалуы қажетті және жеткілікті
барлық
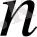 үшін,
үшін,
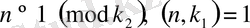 ,
,
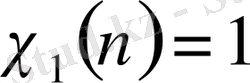 . (1. 1. 15)
. (1. 1. 15)
Дәлелдеу.
Егер
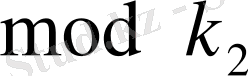 бойынша
бойынша
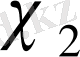 сипаты
сипаты
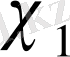 сипатына эквивалентті болса, онда (1. 1. 15) шартын қанағаттандыратын барлық
сипатына эквивалентті болса, онда (1. 1. 15) шартын қанағаттандыратын барлық
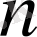 үшін
үшін
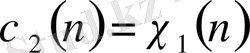 болуы керектігінен қажеттілігі шығады. Бірақ,
болуы керектігінен қажеттілігі шығады. Бірақ,
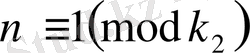 болғандықтан, осы
болғандықтан, осы
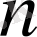 үшін
үшін
 болуы қажет.
болуы қажет.
Керісінше, (1. 1. 15) шарты орынды деп жорамалдайық. Әрбір
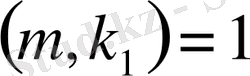 мен
мен
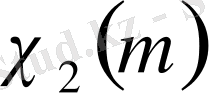 мәнін салыстырамыз. Лемма 1. 1. 2. тәрізді
мәнін салыстырамыз. Лемма 1. 1. 2. тәрізді
 шешімін анықтаймыз және
шешімін анықтаймыз және
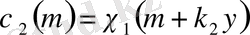 (1. 1. 16 )
(1. 1. 16 )
деп жорамалдаймыз. Бұл анықтаманың
 ті таңдауға қатысы жоқ. Мысалы,
ті таңдауға қатысы жоқ. Мысалы,
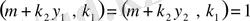 алайық.
алайық.
 ді
ді
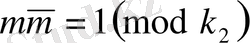 салыстыру көмегімен анықтайық.
салыстыру көмегімен анықтайық.
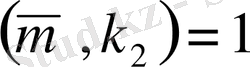 болғандықтан және лемма 1. 1. 2 бойынша
болғандықтан және лемма 1. 1. 2 бойынша
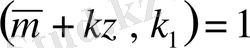 теңдігі орындалатындай
z
бар болатыны анық. Онда
теңдігі орындалатындай
z
бар болатыны анық. Онда
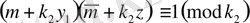 теңдігіне ие боламыз және
теңдігіне ие боламыз және
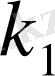 мен бірге екі көбейткіш өз ара жай болады. Осы әдіспен, егер (1. 1. 15) дұрыс деп жорамалдасақ, онда
мен бірге екі көбейткіш өз ара жай болады. Осы әдіспен, егер (1. 1. 15) дұрыс деп жорамалдасақ, онда
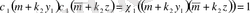
арақатынасына ие боламыз. Сонымен қатар
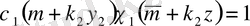
болады.

болғандықтан, осы жерден
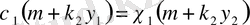
теңдігін аламыз.
Егер
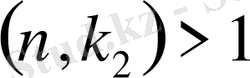 үшін
үшін
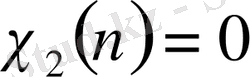 деп жорамалдасақ, онда (1. 1. 16) теңдік көмегімен
деп жорамалдасақ, онда (1. 1. 16) теңдік көмегімен
 бойынша сипат толық анықталады. Бұған көз жеткізу үшін 1-ші және 2-ші, 3-ші шарттарды тексеру жеткілікті.
бойынша сипат толық анықталады. Бұған көз жеткізу үшін 1-ші және 2-ші, 3-ші шарттарды тексеру жеткілікті.
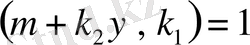 теңдігінен
теңдігінен
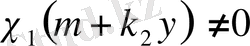
шығатындығынан 1-ші шарт орынды екенін көруге болады. Мысалға,
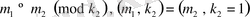 деп алсақ, 2-ші шартты тексеруге болады.
деп алсақ, 2-ші шартты тексеруге болады.
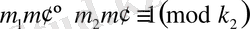 салыстыруынан
салыстыруынан
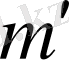 ті анықтаймыз. Содан кейін
ті анықтаймыз. Содан кейін
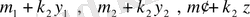
сандары
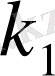 мен өз ара жай болатындай
мен өз ара жай болатындай
 сандарын анықтаймыз. Онда (1. 1. 15) ден
сандарын анықтаймыз. Онда (1. 1. 15) ден
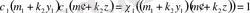
және де
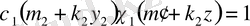
шығады. Сонымен біз
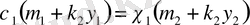 , яғни
, яғни
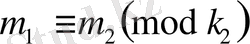 үшін
үшін
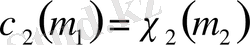 теңдігін алдық. 3-ші шарт
теңдігін алдық. 3-ші шарт
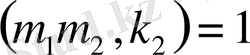 болғанда
болғанда
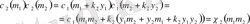
теңдігінен шығады.
Лемма 1. 1. 4.
Егер
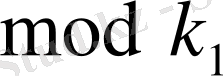 бойынша
бойынша
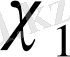 сипаты және
сипаты және
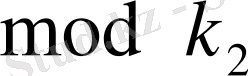 бойынша
бойынша
 сипаты эквивалентті және
сипаты эквивалентті және
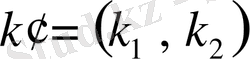 болса, онда
болса, онда
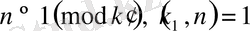 үшін
үшін
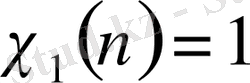
және
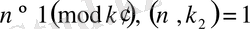 үшін
үшін
 (1. 1. 17)
(1. 1. 17)
теңдіктері орындалады және
 бойынша
бойынша
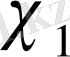 ,
,
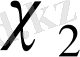 анықталуы мүмкін.
анықталуы мүмкін.
Дәлелдеу.
Айталық,
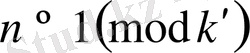 болсын. Мысалы,
болсын. Мысалы,
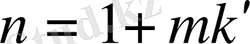 . Егер
. Егер
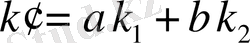 (
(
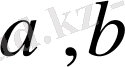 -бүтін сандар) болса, онда
-бүтін сандар) болса, онда
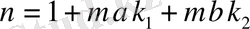 . Енді
. Енді
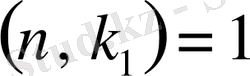 деп алсақ, онда
деп алсақ, онда
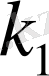 және
және
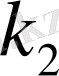 мен
мен
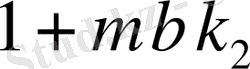 өз ара жай болады және эквиваленттіліктің анықтамасы бойынша
өз ара жай болады және эквиваленттіліктің анықтамасы бойынша
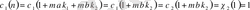
болады. Осылай (1. 1. 17) арақатынасынан 2-ші шарт дәлелденеді және 1. 1. 3 леммасынан осы дәлелденген лемма шығады.
Теорема 1. 1. 3.
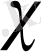 сипатының барлық анықтайтын модульдері жалғыз анықталатын
сипатының барлық анықтайтын модульдері жалғыз анықталатын

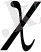 үшін бастаушы деп аталатын модуліне бөлінеді.
үшін бастаушы деп аталатын модуліне бөлінеді.
Дәлелдеу.
Айталық,
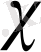 сипатының ең кіші анықтайтын
сипатының ең кіші анықтайтын
 модулі бірден артық болсын. Әрбір басқа анықтайтын модуль
модулі бірден артық болсын. Әрбір басқа анықтайтын модуль
 ға бөлінсін. Қарама қарсы жағдайда
ға бөлінсін. Қарама қарсы жағдайда
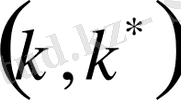 саны тағы да анықтайтын модулі болушы еді (1. 1. 4 леммасы бойынша) және
саны тағы да анықтайтын модулі болушы еді (1. 1. 4 леммасы бойынша) және
 теңсіздігіне ие болады ( біз сипаттар үшін эквивалентіліктің транзитивті арақатынасын қолдандық) . Егер ең кіші анықтайтын модуль бірге тең болса, онда теорема орынды екені анық.
теңсіздігіне ие болады ( біз сипаттар үшін эквивалентіліктің транзитивті арақатынасын қолдандық) . Егер ең кіші анықтайтын модуль бірге тең болса, онда теорема орынды екені анық.
Одан әрі ең кіші анықтайтын модульді
 арқылы, ал
арқылы, ал
 бойынша
бойынша
 эквивалентті сипатын
эквивалентті сипатын
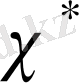 арқылы белгілейміз.
арқылы белгілейміз.
 бойынша сипаты үшін
бойынша сипаты үшін
 эквиваленттілігі бар. Мұндағы барлық
эквиваленттілігі бар. Мұндағы барлық
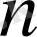 үшін
үшін
 да екі сипаты бірдей мәнге ие болмайды.
да екі сипаты бірдей мәнге ие болмайды.
Мысалы,
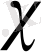 -
-
 бойынша сипат, сонымен бірге
бойынша сипат, сонымен бірге
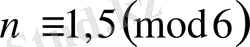 үшін
үшін
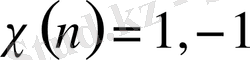 болсын. Мұнда
болсын. Мұнда
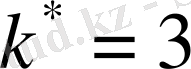 -
-
 сипатының бастаушы модулі, ал
сипатының бастаушы модулі, ал
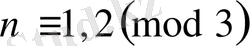 үшін
үшін
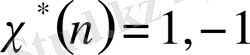 .
.
Егер
 бойынша
бойынша
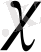 сипаты
сипаты
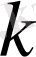 ны бөлетін ешқандай модульмен анықталмаса, онда
ны бөлетін ешқандай модульмен анықталмаса, онда
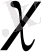 сипаты примитивті сипат деп аталады. Онда
сипаты примитивті сипат деп аталады. Онда
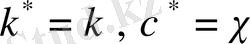 теңдіктеріне ие боламыз. Дербес жағдайда,
теңдіктеріне ие боламыз. Дербес жағдайда,
 -барлық уақытта примитивті сипат (демек,
-барлық уақытта примитивті сипат (демек,
 ) . Осы тәсілмен әрбір сипатқа жалғыз
) . Осы тәсілмен әрбір сипатқа жалғыз
 примитивті сипаты сәйкес қойылады. Екі эквивалентті сипаттары бір примитивті сипатқа ие болады. Әрбір модулі бойынша берілген сипат үшін ең болмағанда бір эквивалентті сипат бар болады.
примитивті сипаты сәйкес қойылады. Екі эквивалентті сипаттары бір примитивті сипатқа ие болады. Әрбір модулі бойынша берілген сипат үшін ең болмағанда бір эквивалентті сипат бар болады.
 жиыны
жиыны
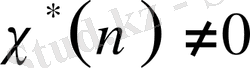 мен бірге, жалпы айтқанда,
мен бірге, жалпы айтқанда,
 жиын ұзындығы
жиын ұзындығы
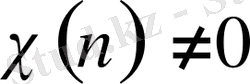 мен бірге. Осы жиындардан
мен бірге. Осы жиындардан
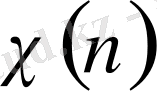 функциясы сипат қасиеттерінен арылмайтындай ең үлкен жиыны бар болады.
функциясы сипат қасиеттерінен арылмайтындай ең үлкен жиыны бар болады.
Берілген сипат примитивті ме, әлде примитивті емес пе екенін тексеру үшін лемма 1. 1. 3 бойынша әрбір
 үшін
үшін
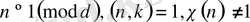
болатындай ең болмағанда бір
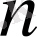 бар болуын тексеру қажет.
бар болуын тексеру қажет.
Екі примитивті сипаттар барлық
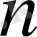 үшін сәйкес келеді немесе эквивалентті емес болады.
үшін сәйкес келеді немесе эквивалентті емес болады.
Дербес жағдайда,
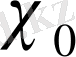 бас сипаты әрбір
бас сипаты әрбір
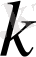 үшін
үшін
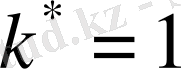 бас модуліне және барлық
бас модуліне және барлық
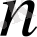 бүтін саны үшін
бүтін саны үшін
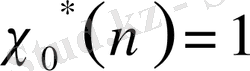 теңдігіне ие боламыз.
теңдігіне ие боламыз.
Егер
 нақты сипат болса, онда
нақты сипат болса, онда
 да нақты сипат болады. Мұны (1. 1. 16) теңдігінен көруге болады, яғни
да нақты сипат болады. Мұны (1. 1. 16) теңдігінен көруге болады, яғни
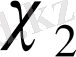 нақты сипат болады, егер
нақты сипат болады, егер
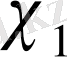 нақты сипат болса.
нақты сипат болса.
§ 1. 2. Дирехле функциясының анықтамасы және қасиеттері.
Дирехле қатары деп аталатын
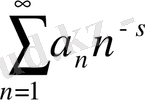 шектеусіз қатарды қарастырайық. Мұнда
шектеусіз қатарды қарастырайық. Мұнда
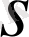 -комплекс сан және
-комплекс сан және
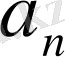 коэффициенттері де комплекс сандары болып табылады. Егер
коэффициенттері де комплекс сандары болып табылады. Егер
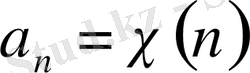 десек, онда
десек, онда
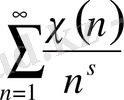 ,
,
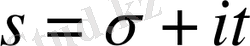 , (1. 2. 1)
, (1. 2. 1)
болады. Мұндағы
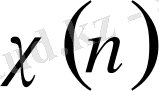 -сандық функция, Дирехле сипаты деп аталады
-сандық функция, Дирехле сипаты деп аталады
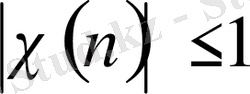 .
.
Дирехле қатары
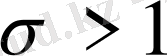 жарты жазықтықта жатқан әрбір шектеулі облыста абсолют және бірқалыпты жинақты болады және де регуляр аналитикалық
жарты жазықтықта жатқан әрбір шектеулі облыста абсолют және бірқалыпты жинақты болады және де регуляр аналитикалық
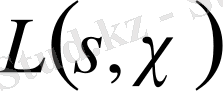 функциясын өрнектейді. Мұнымен бірге,
функциясын өрнектейді. Мұнымен бірге,
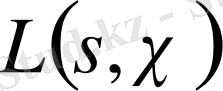 функциясы тұтас комплекс жазықтыққа аналитикалық жолмен созылуы мүмкін. Біз
функциясы тұтас комплекс жазықтыққа аналитикалық жолмен созылуы мүмкін. Біз
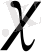 түрліше сипаттары үшін
түрліше сипаттары үшін
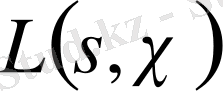 әр түрлі функцияларды аламыз. Мұнда, егер
әр түрлі функцияларды аламыз. Мұнда, егер
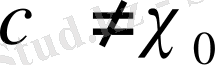 болса, онда
болса, онда
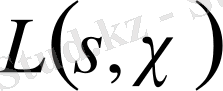 функциясының комплекс жазықтықтың шектеулі бөлігінде ерекше нүктелері болмайды, ол-бүтін функция. Егер
функциясының комплекс жазықтықтың шектеулі бөлігінде ерекше нүктелері болмайды, ол-бүтін функция. Егер
 болса, онда
болса, онда
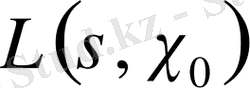 функциясының
функциясының
 нүктесінде жалғыз ғана жай полюсі болады.
нүктесінде жалғыз ғана жай полюсі болады.
Риманның дзета-функциясын Дирехле қатарының дербес жағдайы ретінде қарастыруға болады. Егер
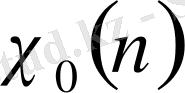 -бас сипат, яғни
-бас сипат, яғни
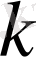 -мен өз ара жай болатын барлық натурал
-мен өз ара жай болатын барлық натурал
 үшін
үшін
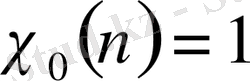 болса, онда
болса, онда
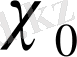 сипатқа сәйкес
сипатқа сәйкес
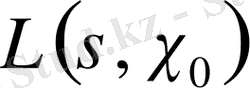 Дирехле функциясының Риманның
Дирехле функциясының Риманның
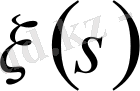 дзета-функциясынан айырмашылығы тек тұрақты көбейіткіште ғана болады, өйткені
дзета-функциясынан айырмашылығы тек тұрақты көбейіткіште ғана болады, өйткені
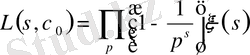 ,
,
мұнда
 шамасы
шамасы
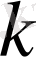 санының барлық жай бөлгіштерін қабылдайды.
санының барлық жай бөлгіштерін қабылдайды.
 функцияларының қасиеттерін қарастыру барысында мына екі жағдайды байқау қиын емес:
функцияларының қасиеттерін қарастыру барысында мына екі жағдайды байқау қиын емес:
- сипаты қашан бас сипат
- қашан
болады.
Теорема 1. 2. 1.
Егер
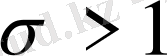 болса, онда кез келген
k
модулі бойынша
болса, онда кез келген
k
модулі бойынша
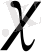 үшін төмендегі жіктеуі
үшін төмендегі жіктеуі
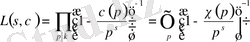 (1. 2. 2)
(1. 2. 2)
орындалады.
Бұл тұжырым мына теоремадан шығады:
Айталық,
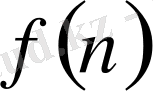 -барлық натурал
-барлық натурал
 үшін анықталған нақты немесе комплексті мультипликатты функция болсын, яғни
үшін анықталған нақты немесе комплексті мультипликатты функция болсын, яғни
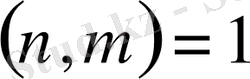 және
және
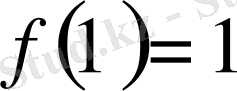 болғанда
болғанда
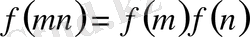 . Егер
. Егер
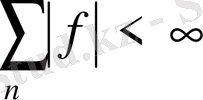 болса, онда
болса, онда
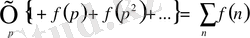 .
.
Егер
 болғанда
болғанда
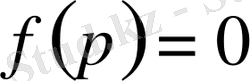 және
және
 болғанда
болғанда
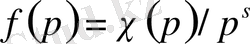 деп ұйғарсақ және мына арақатынастан
деп ұйғарсақ және мына арақатынастан
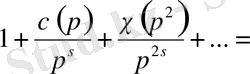
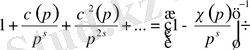 .
.
Дербес жағдай ретінде мына формула орынды
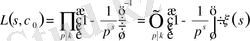
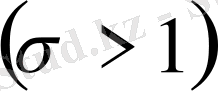 . (1. 2. 3)
. (1. 2. 3)
Мысалы,
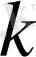 =2 болғанда тек
=2 болғанда тек
 негізгі сипат бар болады, сондықтан
негізгі сипат бар болады, сондықтан
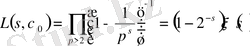 .
.
 =3 болғанда
=3 болғанда
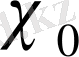 және
және
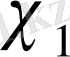 екі сипат бар болады.
екі сипат бар болады.
 үшін
үшін
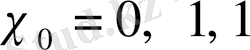 және
және
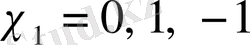 . Онда мына теңдіктерге ие боламыз
. Онда мына теңдіктерге ие боламыз
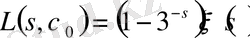 ,
,
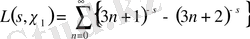 .
.
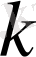 =4 болғанда
=4 болғанда
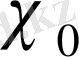 және
және
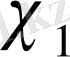 екі сипат бар болады.
екі сипат бар болады.
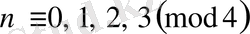 үшін
үшін
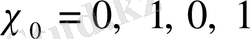 және
және
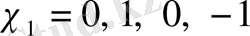 . Сондықтан,
. Сондықтан,
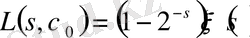 ,
,
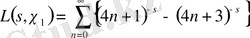 .
.
Теоерма 1. 2. 2.
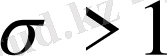 облысында кез келген
облысында кез келген
 үшін
үшін
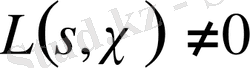 болады.
болады.
Расында да, (1. 2. 2) формуладан мына теңсіздікті аламыз
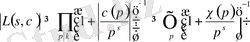 .
.
Осы теоремадан (1. 2. 2) формуланы логарифмдеуге болатыны шығады:
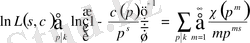 ,
,
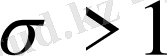 .
.
Мұндағы қос қатар мына мәнді көрсетеді
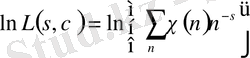 , мұнда егер
, мұнда егер
 , онда осы мән нөлге ұмтылады.
, онда осы мән нөлге ұмтылады.
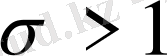 болғанда
болғанда
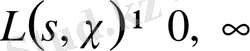 болғандықтан, бұл логарифмнің тармағы
болғандықтан, бұл логарифмнің тармағы
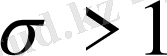 облысында бірмәнді және регулярлы болады. Мұндағы қос қатар жинақты, сондықтан қатардың ретін ауыстыруға болады.
облысында бірмәнді және регулярлы болады. Мұндағы қос қатар жинақты, сондықтан қатардың ретін ауыстыруға болады.
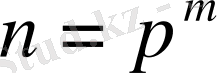 және
және
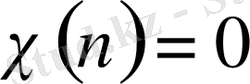 болғанда
болғанда
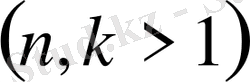 болғандықтан,
болғандықтан,
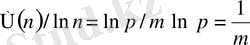 болады, онда келесі формуланы аламыз
болады, онда келесі формуланы аламыз
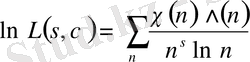 ,
,
 . (1. 2. 4)
. (1. 2. 4)
Жоғарғы теңдікті дифференциалдау арқылы төмендегі теңдікке ие боламыз
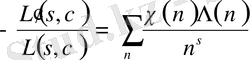 ,
,
 , (1. 2. 5)
, (1. 2. 5)
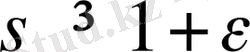 болғанда ақырғы қатар бірқалыпты жинақталатындықтан дифференциялдау заңы орынды.
болғанда ақырғы қатар бірқалыпты жинақталатындықтан дифференциялдау заңы орынды.
Теорема 1. 2. 3.
Егер
 облысында
облысында
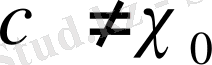 болса, онда
болса, онда
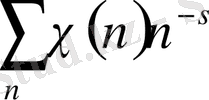 қатары жинақты болады.
қатары жинақты болады.
 облысында барлық
облысында барлық
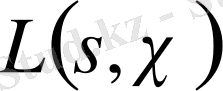 функциялары және
функциялары және
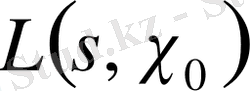 функциясын қосқанда аналитикалық жолмен созылады және регулярлы болады.
функциясын қосқанда аналитикалық жолмен созылады және регулярлы болады.
 нүктесінде және
нүктесінде және
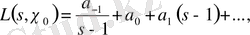
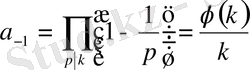 (1. 2. 6)
(1. 2. 6)
түріндегі жіктеуіне ие боламыз.
Дәлелдеу.
Айталық,
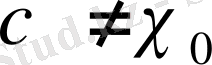 болсын.
болсын.
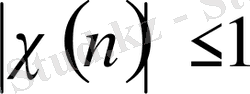 теңсіздігінен және
теңсіздігінен және
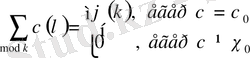 формуласынан кез келген
формуласынан кез келген
 үшін
үшін
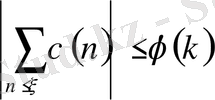 (1. 2. 7)
(1. 2. 7)
аламыз. Соңғы қатар
 арқылы
арқылы
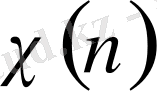 тізбегінің мүшесі нөлге айналады.
тізбегінің мүшесі нөлге айналады.
Теорема.
Айталық,
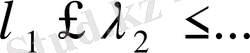 - нақты сандардың тізбегі,
- нақты сандардың тізбегі,
 және
және
 -
-
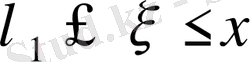 кесіндісінде үзіліссіз дифференциалданған (нақты немесе комплексті) функция болсын. Онда
кесіндісінде үзіліссіз дифференциалданған (нақты немесе комплексті) функция болсын. Онда
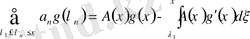 . (***)
. (***)
Мұндағы
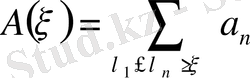 және
және
 -кез келген комплексті сан. Егер (***) да
-кез келген комплексті сан. Егер (***) да
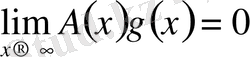 және не қатар, не инеграл жинақты болса, онда
және не қатар, не инеграл жинақты болса, онда
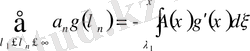
Теоремасынан
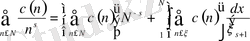 (1. 2. 8)
(1. 2. 8)
аламыз.
 болғанда соңғы интеграл (1. 2. 7) теңсіздік нәтижесінде жинақталады.
болғанда соңғы интеграл (1. 2. 7) теңсіздік нәтижесінде жинақталады.
 болғанда біздің тұжырымымыз 1. 1. 1. теоремасынан шығады.
болғанда біздің тұжырымымыз 1. 1. 1. теоремасынан шығады.
 болғанда ол (1. 2. 3) формуладан және 1. 2. 1 теоремасынан шығады.
болғанда ол (1. 2. 3) формуладан және 1. 2. 1 теоремасынан шығады.
Дербес жағдайда,
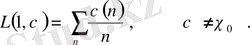 (1. 2. 9)
(1. 2. 9)
Ақырсыз көп сандар
 бар екенін дәлелдеу үшін мына қатынасты дәлелдеу жеткілікті
бар екенін дәлелдеу үшін мына қатынасты дәлелдеу жеткілікті
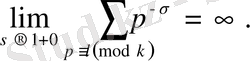 (1. 2. 10)
(1. 2. 10)
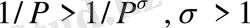 болса, онда (1. 2. 10) теңдіктен
болса, онда (1. 2. 10) теңдіктен
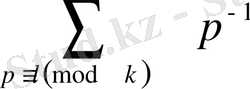 қатарының жинақсыздығы шығады. Осыдан
қатарының жинақсыздығы шығады. Осыдан
 , (1. 2. 11)
, (1. 2. 11)
теңдіктің оң жақ бөлігінің қосындысы барлық
р
үшін жүргізіледі.
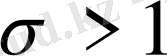 болғанда (1. 2. 4) бойынша теңдік орнына
болғанда (1. 2. 4) бойынша теңдік орнына
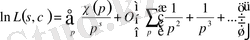
аламыз және сондықтан
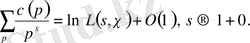
(1. 2. 11) теңдігінен
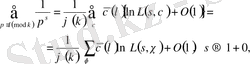 (1. 2. 12)
(1. 2. 12)
шығады, мұнда
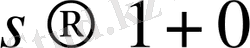 өрнегі s нақты мәндерді қабылдай отыра, оң жақтан бірге ұмтылады дегенді білдіреді. Мөлшер мүшесі
өрнегі s нақты мәндерді қабылдай отыра, оң жақтан бірге ұмтылады дегенді білдіреді. Мөлшер мүшесі
 түрінде болса,
түрінде болса,
 де тұрақты сан
k
дан тәуелсіз, қатарда кездестірілген
де тұрақты сан
k
дан тәуелсіз, қатарда кездестірілген
 әр түрлі. (1. 2. 6) теңдігінен
әр түрлі. (1. 2. 6) теңдігінен
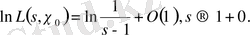 (1. 2. 13)
(1. 2. 13)
аламыз. Нәтижесінде
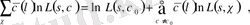
(1. 2. 12) және (1. 2. 13) теңдіктерінен (1. 2. 10) теңдік шығады. Оған көз жеткізу үшін, бізге
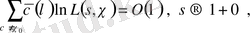 (1. 2. 14)
(1. 2. 14)
болатынын дәлелдеу жеткілікті немесе
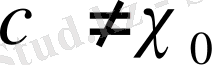 болғанда
болғанда
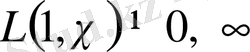 болатындығын.
болатындығын.
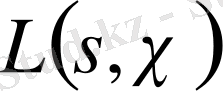 функциясының регулярлығынан
функциясының регулярлығынан
 болғанда
болғанда
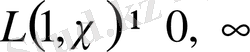 (
(
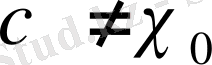 ) шығады.
) шығады.
§ 1. 3.
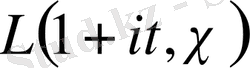 функциясының нөлге айналмауы.
функциясының нөлге айналмауы.
 шексіз көп жай сандар бар екенін анықтау үшін
шексіз көп жай сандар бар екенін анықтау үшін
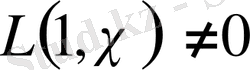 (1. 3. 1)
(1. 3. 1)
арақатынасын дәлелдейміз. Ол кезде екі жағдайды ажыратуымыз керек:
- ең болмағанда бірnкомплекс мәні үшін қабылдайды;
- барлықn- нақты сандар үшін.
Бірінші жағдайда
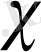 комплекстік сипат, ал екінші жағдайда нақты сипат деп аталады.
комплекстік сипат, ал екінші жағдайда нақты сипат деп аталады.
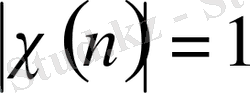 немесе 0 болғандықтан
немесе 0 болғандықтан
 нақты сипаты
нақты сипаты
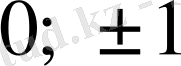 мәндеріне тең болуы керек. Сондықтан
мәндеріне тең болуы керек. Сондықтан
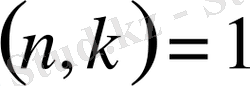 үшін
үшін
 және
және
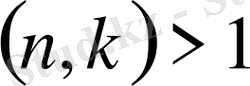 үшін
үшін
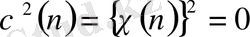 . Осыдан сипатының комплексті немесе нақты екені шығады. Енді
. Осыдан сипатының комплексті немесе нақты екені шығады. Енді
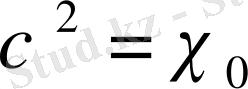 немесе
немесе
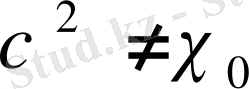 жағдайын қарастырайық.
жағдайын қарастырайық.
Теорема 1. 3. 1.
Егер
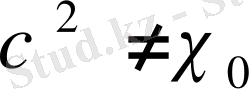 болса, онда барлық t үшін
болса, онда барлық t үшін
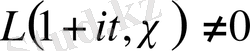 (1. 3. 2)
(1. 3. 2)
орындалады және
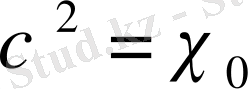 ,
,
 болса, онда
болса, онда
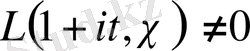 (1. 3. 3)
(1. 3. 3)
теңдігі орындалады.
Дәлелдеу.
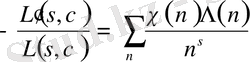 теңдігінен
теңдігінен
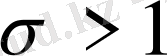 болғанда
болғанда
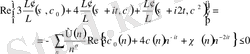 (1. 3. 4)
(1. 3. 4)
теңдігін аламыз.
Мұндағы
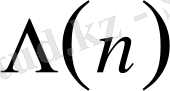 -монғолт функциясы деп аталады,
-монғолт функциясы деп аталады,
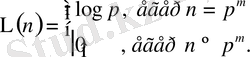
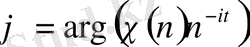 деп ұйғарсақ, онда
деп ұйғарсақ, онда
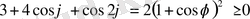 .
.
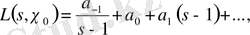 теңдігінен
теңдігінен
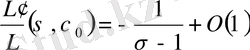 ,
,
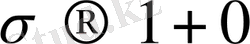 (1. 3. 5)
(1. 3. 5)
шығады. Егер де
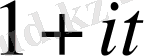 саны
саны
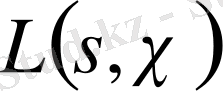 функциясының нөлі болса, мысалы, m ретті,
функциясының нөлі болса, мысалы, m ретті,
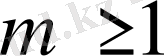 , онда біз
, онда біз
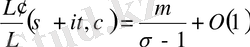 ,
,
 (1. 3. 6)
(1. 3. 6)
теңдігіне ие болар едік. Теорема 1. 2. 3. бойынша
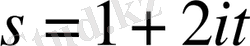 -
-
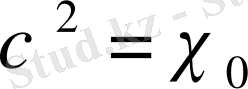 ,
,
 болмаған жағдайда
болмаған жағдайда
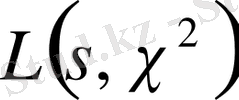 функциясының регулярлы нүктесі болады. Осы жағдайдан кейін
функциясының регулярлы нүктесі болады. Осы жағдайдан кейін
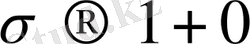 болғанда
болғанда
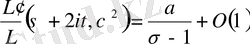 ,
,
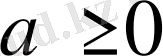 (1. 3. 7)
(1. 3. 7)
теңдігін аламыз. (1. 3. 5), (1. 3. 6), (1. 3. 7) формулаларынан
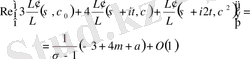 ,
,
 (1. 3. 8)
(1. 3. 8)
шығады. Мұнда
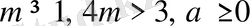 болғандықтан, бұл (1. 3. 3) формуласына қайшылыққа келеді. Осыдан
болғандықтан, бұл (1. 3. 3) формуласына қайшылыққа келеді. Осыдан
 деген жорамалдауымыз дұрыс емес және (1. 3. 1), (1. 3. 2) формулалары тура екені шығады.
деген жорамалдауымыз дұрыс емес және (1. 3. 1), (1. 3. 2) формулалары тура екені шығады.
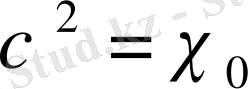 ,
,
 болған жағдайды қарастырайық.
болған жағдайды қарастырайық.
Лемма 1. 3. 1
Егер
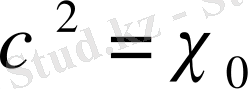 , болса, онда
, болса, онда
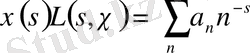 ,
,
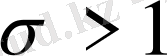 , (1. 3. 9)
, (1. 3. 9)
теңдігі орынды болады, мұндағы
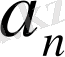 -нақты сан және
-нақты сан және
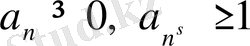 . (1. 3. 10)
. (1. 3. 10)
Дәлелдеу.
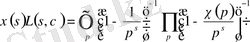
теңдігін қарастырайық.
 сипаты тек
сипаты тек
 мәндерін ғана қабылдайды.
мәндерін ғана қабылдайды.
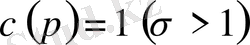 үшін
үшін
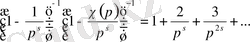 ;
;
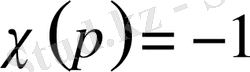 үшін
үшін
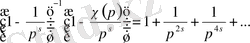
және
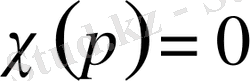 үшін
үшін
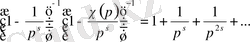
орындалады. Осы барлық үш түрдегі көбейтінділерді көбейтетін болсақ, онда коэффициенттері
 болатын Дирехле қатарын аламыз. Үш жағдайда да коэффициенттер
болатын Дирехле қатарын аламыз. Үш жағдайда да коэффициенттер
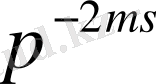 болғанда бірден кем емес болады.
болғанда бірден кем емес болады.
Теорема 1. 3. 2.
Егер
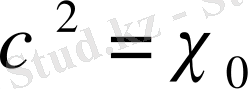 ,
,
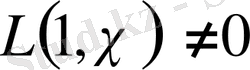 және
және
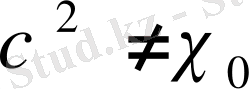 болса, онда
болса, онда
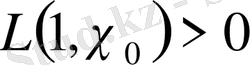 (1. 3. 11)
(1. 3. 11)
теңсіздік орындалады.
Дәлелдеу.
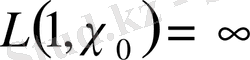 болғандықтан,
болғандықтан,
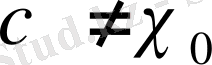 жағдайын зерттейміз. (1. 3. 9) формуласындағы қатарды қарастырамыз.
жағдайын зерттейміз. (1. 3. 9) формуласындағы қатарды қарастырамыз.
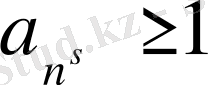 ,
,
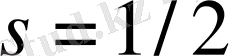 болғанда
болғанда
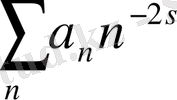 жартылай қатары жинақсыз болады. Сондықтан
жартылай қатары жинақсыз болады. Сондықтан
 болғанда
болғанда
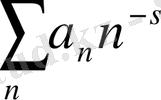 қатары жинақсыз болады. Осы қатардың
қатары жинақсыз болады. Осы қатардың
 абциссасы жинақты болуы үшін
абциссасы жинақты болуы үшін
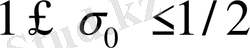 теңсіздігі орындалуы қажет. Басқаша айтқанда, Ландау теоремасы бойынша
s=
теңсіздігі орындалуы қажет. Басқаша айтқанда, Ландау теоремасы бойынша
s=
 -
-
 функциясының негізгі нүктесі.
функциясының негізгі нүктесі.
Теорема.
Егер
 саны-
саны-
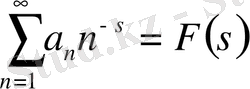 қатарының абцисса жинақтығы, барлық
қатарының абцисса жинақтығы, барлық
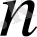 үшін
үшін
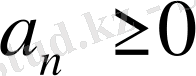 брлса, онда
брлса, онда
 болатын
болатын
 ерекше нүктесі бар болады.
ерекше нүктесі бар болады.
Бірақ,
 болғанда
болғанда
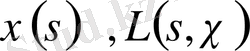 функциялары регулярлы, онда
функциялары регулярлы, онда
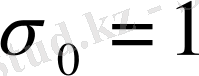 болуы қажет. Бірақ, онда
болуы қажет. Бірақ, онда

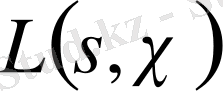 функциясының нөлі бола алмайды. Расында да, қарама қарсы жағдайда
функциясының нөлі бола алмайды. Расында да, қарама қарсы жағдайда
 болғанда
болғанда
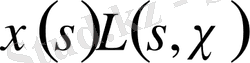 функциясы регулярлы болуы мүмкін еді.
функциясы регулярлы болуы мүмкін еді.
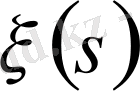 бірінші ретті полюс болғандықтан
бірінші ретті полюс болғандықтан
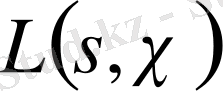 реті бірден артық нөлі компенсірілген. Сондықтан,
реті бірден артық нөлі компенсірілген. Сондықтан,
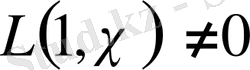 .
.
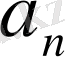 оң болса және
оң болса және
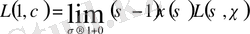
теңдігінен
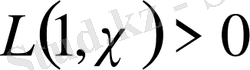 болатыны шығады.
болатыны шығады.
Теорема 1. 3. 3.
Егер
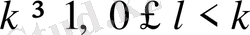 және
және
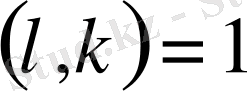 болса, онда
болса, онда
 түріндегі бірнеше жай сандар бар болады:
түріндегі бірнеше жай сандар бар болады:
 (1. 3. 12)
(1. 3. 12)
Дәлелдеу.
1. 3. 2 және 1. 3. 3 теоремалары бойынша
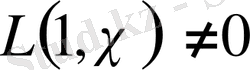 барлық сипаттары
барлық сипаттары
 үшін. Осыдан (1. 2. 13) формуласы шығады және (1. 2. 11), (1. 2. 12) формулаларынан (1. 2. 9) шығады. Осымен теорема дәлелденеді.
үшін. Осыдан (1. 2. 13) формуласы шығады және (1. 2. 11), (1. 2. 12) формулаларынан (1. 2. 9) шығады. Осымен теорема дәлелденеді.
(1. 2. 10) және (1. 2. 11) формулаларымен бірге теорема 1. 3. 3 дәлелдеу үшін ұқсас дәлелденген мына теңдікті алуға болады
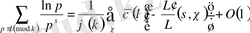 (1. 3. 13)
(1. 3. 13)
Онда (1. 2. 10) формуласынан
 болғанда
болғанда
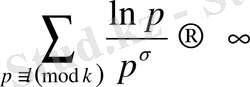 (1. 3. 14)
(1. 3. 14)
арақатынасын аламыз.
§ 1. 4.
 функциясының нөлдері туралы.
функциясының нөлдері туралы.
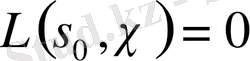 шарты орындалатын
шарты орындалатын
 нүктелері
нүктелері
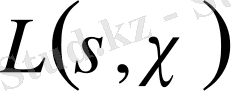 функциясының нөлдері деп аталады.
функциясының нөлдері деп аталады.
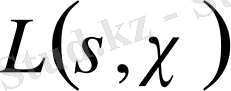 функциясының барлық нөлдері ені
функциясының барлық нөлдері ені
 шектеулі, жорымал оське параллель болатын шектеусіз жолақта жататындығы дәлелденген. Дирехле функцияларының нөлдері жөнінде мынадай гипотеза бар: бұл функциялардың
шектеулі, жорымал оське параллель болатын шектеусіз жолақта жататындығы дәлелденген. Дирехле функцияларының нөлдері жөнінде мынадай гипотеза бар: бұл функциялардың
 жолағында (кризистік жолақта) жататын барлық нөлдері
жолағында (кризистік жолақта) жататын барлық нөлдері
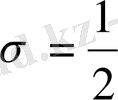 түзуінің бойында орналасады.
түзуінің бойында орналасады.
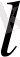 және
және
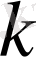 өз ара жай сандарын қарастырамыз.
өз ара жай сандарын қарастырамыз.
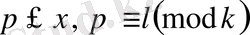 үшін
үшін
 жай санын
жай санын
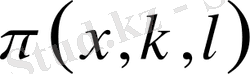 арқылы белгілейміз
арқылы белгілейміз
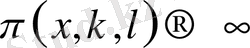 (
(
 ) .
) .
Біздің негізгі мақсатымыз
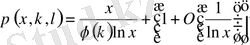 (1. 4. 1)
(1. 4. 1)
арақатынасын дәлелдеу.
Асимптотикалық формулаларды алу үшін бірнеше
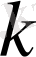 мәніндегі облысында теңдік орынды болу керектігін көрсетуіміз қажет. Ол үшін біз
мәніндегі облысында теңдік орынды болу керектігін көрсетуіміз қажет. Ол үшін біз
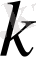 бойынша барлық бағалау теңдіктерін, яғни тұрақты санымыз
бойынша барлық бағалау теңдіктерін, яғни тұрақты санымыз
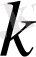 дан тәуелсіз болуын дәлелдеуіміз керек.
дан тәуелсіз болуын дәлелдеуіміз керек.
Теорема 1. 4. 1
. Егер
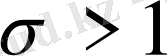 болса, онда
болса, онда
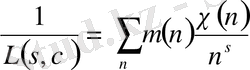 (1. 4. 2)
(1. 4. 2)
теңдігі орынды болады. Мұндағы
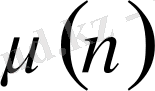 -Мёбиус функиясы,
-Мёбиус функиясы,
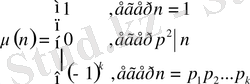 .
.
Дәлелдеу.
Айталық,
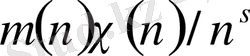 -мультипликатты функция болсын. Онда бұл теорема 1. 2. 1 және мына теоремадан шығады.
-мультипликатты функция болсын. Онда бұл теорема 1. 2. 1 және мына теоремадан шығады.
Теорема.
Айталық,
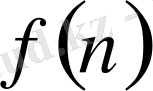 -барлық
-барлық
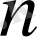 натурал үшін анықталған нақты немесе комплексті мультипликатты функция болсын. Егер
натурал үшін анықталған нақты немесе комплексті мультипликатты функция болсын. Егер
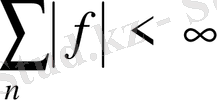 болса, онда
болса, онда
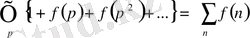 .
.
Мақсатқа сәйкес
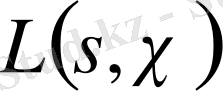 бағалауы үшін көмекші функциясын енгіземіз
бағалауы үшін көмекші функциясын енгіземіз
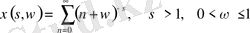 . (1. 4. 3)
. (1. 4. 3)
Дербес жағдайда,
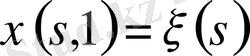 . Онда
. Онда
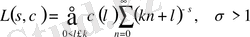
болатыны анық. Сондықтан,
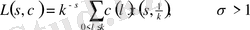 . (1. 4. 4)
. (1. 4. 4)
(1. 4. 4 ) формуласы осы облыста орынды болады, себебі
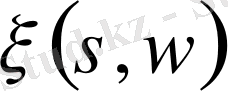 функциясы
функциясы
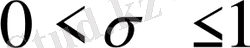 облысында аналитикалық жалғасады.
облысында аналитикалық жалғасады.
Теорема 1
.
4. 2.
Егер
 және
және
 -оң тұрақты сан және
-оң тұрақты сан және
 облысында
облысында
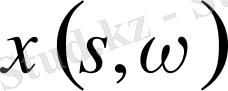 функциясы аналитикалық жолмен созылуы мүмкін болса, онда
функциясы аналитикалық жолмен созылуы мүмкін болса, онда
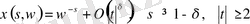 ; (1. 4. 5)
; (1. 4. 5)
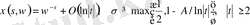 (1. 4. 6)
(1. 4. 6)
арақатынастарына ие боламыз. Мұнда
 нүктесінде
нүктесінде
 және сәйкес
және сәйкес
 тәуелді, бірақ
тәуелді, бірақ
 дан тәуелсіз.
дан тәуелсіз.
Дәлелдеу.
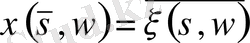 болғандықтан теореманы
болғандықтан теореманы
 үшін дәлелдеу жеткілікті.
үшін дәлелдеу жеткілікті.
 болғанда
болғанда
 болғандықтан
болғандықтан
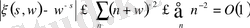
аламыз. Демек,
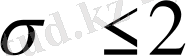 деп жорамалдауымызға болады.
деп жорамалдауымызға болады.
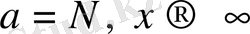 үшін және
үшін және
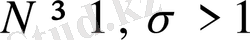 болғанда
болғанда
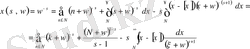 (1. 4. 7)
(1. 4. 7)
теңдігін аламыз. Бұл формула
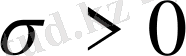 облысында
облысында
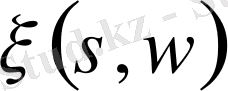 функциясының аналитикалық ұластыруын береді.
функциясының аналитикалық ұластыруын береді.
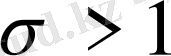 болғанда соңғы интегралдағы функция регулярлы болады.
болғанда соңғы интегралдағы функция регулярлы болады.
 теңсіздігі бойынша (1. 4. 7) формуласынан
теңсіздігі бойынша (1. 4. 7) формуласынан
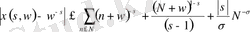
теңсіздігін аламыз.
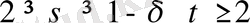 облыстарында кез келген
облыстарында кез келген
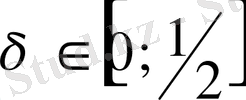 үшін
үшін
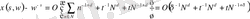 (1. 4. 8)
(1. 4. 8)
бағалауы орынды болады. Мұндағы тұрақты санымыз
 -де
-де
 -дан тәуелсіз. Егер
-дан тәуелсіз. Егер
 ,
,
 бекітулі және
бекітулі және
 -ден тұрақты сандарды
-ден тұрақты сандарды
 -дан тәуелді етсек, онда қалған мүшелеріміз мына түрге ие болады:
-дан тәуелді етсек, онда қалған мүшелеріміз мына түрге ие болады:
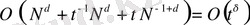 .
.
Басқаша айтқанда, егер біз
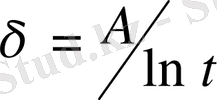 ,
,
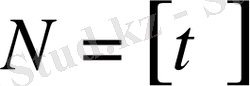 деп алсақ, онда (1. 4. 8) формуласындағы қалған мүшелер мына теңдікке ие болады:
деп алсақ, онда (1. 4. 8) формуласындағы қалған мүшелер мына теңдікке ие болады:
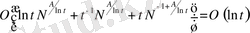 .
.
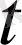 үлкен болғандықтан, мұнда
үлкен болғандықтан, мұнда
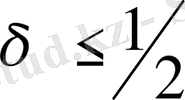 болады.
болады.
Теорема 1. 4. 3.
Егер
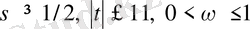 болса, онда
болса, онда
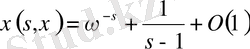 (1. 4. 9)
(1. 4. 9)
арақатынасы орындалады. Мұндағы
 дегі тұрақты сандарымыз
дегі тұрақты сандарымыз
 және
және
 дан тәуелсіз болады.
дан тәуелсіз болады.
Дәлелдеу.
 үшін
үшін
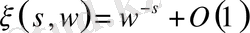 аламыз. Сондықтан, (1. 4. 9) теңдік орынды. Енді (1. 4. 7) формуласында
аламыз. Сондықтан, (1. 4. 9) теңдік орынды. Енді (1. 4. 7) формуласында
 деп жорамалдасақ, онда
деп жорамалдасақ, онда
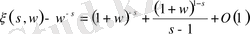
теңдігін аламыз. Мұндағы
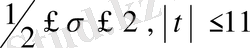 . Осы облыста
. Осы облыста
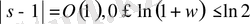 болғандықтан
болғандықтан
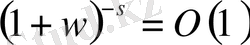 және
және
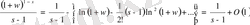
болады.
Теорема 1. 4. 4.
Айталық,
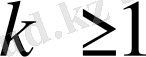 және
және
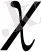 -
-
 бойынша кез келген сипат болсын. Егер
бойынша кез келген сипат болсын. Егер
 ,
,
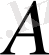 -оң тұрақты сан және
-оң тұрақты сан және
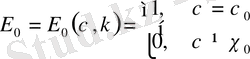 (1. 4. 10)
(1. 4. 10)
болса, онда
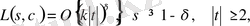 (1. 4. 11)
(1. 4. 11)
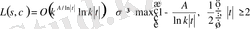 , (1. 4. 12)
, (1. 4. 12)
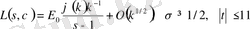 . (1. 4. 13)
. (1. 4. 13)
бағалаулары орындалады. Мұндағы барлық тұрақты сандар
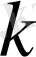 дан тәуелсіз, бірақ
дан тәуелсіз, бірақ
 және сәйкес
және сәйкес
 ға тәуелді болуы мүмкін.
ға тәуелді болуы мүмкін.
Дәлелдеу.
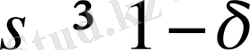 ,
,
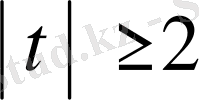 болғанда (1. 4. 4) және (1. 4. 5) формулаларынан
болғанда (1. 4. 4) және (1. 4. 5) формулаларынан
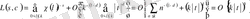
аламыз. Мұндағы тұрақты сан
 де
де
 дан тәуелді болуы мүмкін. Бұл (1. 4. 11) формуласын береді.
дан тәуелді болуы мүмкін. Бұл (1. 4. 11) формуласын береді.
 және
және
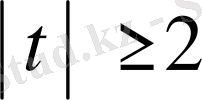 болғанда (1. 4. 4), (1. 4. 6) формулаларынан (1. 4. 12) бағалауы шығады:
болғанда (1. 4. 4), (1. 4. 6) формулаларынан (1. 4. 12) бағалауы шығады:
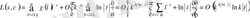 .
.
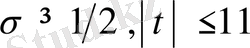 болғанда (1. 4. 5) және (1. 4. 10) формулаларынан
болғанда (1. 4. 5) және (1. 4. 10) формулаларынан
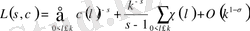 (1. 4. 14)
(1. 4. 14)
шығады. Енді (1. 3. 7) формуласын ескере отыра
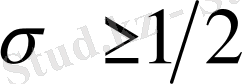 болғанда
болғанда
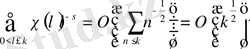 (1. 4. 15)
(1. 4. 15)
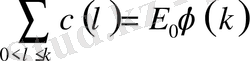 (1. 4. 16)
(1. 4. 16)
аламыз. Одан кейін
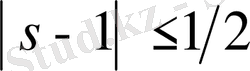 болғанда
болғанда
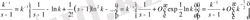 (1. 4. 17)
(1. 4. 17)
теңдігіне ие боламыз. Немесе
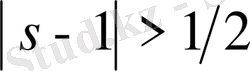 ,
,
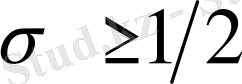 болғанда
болғанда
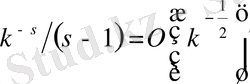 теңдігін аламыз. Мұны және (1. 4. 15), (1. 4. 16) формулаларын (1. 4. 14) формуласына қойсақ, (1. 4. 13) формуласын аламыз.
теңдігін аламыз. Мұны және (1. 4. 15), (1. 4. 16) формулаларын (1. 4. 14) формуласына қойсақ, (1. 4. 13) формуласын аламыз.
 болғанда
болғанда
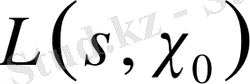 қалыңдысы
қалыңдысы
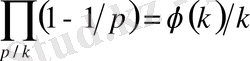 теңдігіне тең болатынындай етіп, біз (1. 2. 5) теңдігінде қойғанбыз.
теңдігіне тең болатынындай етіп, біз (1. 2. 5) теңдігінде қойғанбыз.
Теорема 1. 4. 5.
Егер
 болса, онда
болса, онда
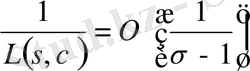 (1. 4. 18)
(1. 4. 18)
бағалауы орынды болады.
Дәлелдеу.
(1. 4. 2) формуласынан және
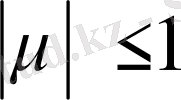 теңсіздігінен
теңсіздігінен
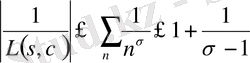
шығады. Демек, (1. 4. 18) орынды болғаны.
Тоерема 1. 4. 6.
Егер
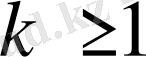 болса, онда
болса, онда
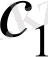 қолайлы болғанда барлық
mod k
бойынша
қолайлы болғанда барлық
mod k
бойынша
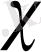 үшін
үшін
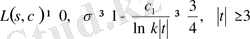 (1. 4. 19)
(1. 4. 19)
теңсіздікке ие боламыз.
Дәлелдеу.
 үшін бұл тұжырымды дәлелдеу жеткілікті. Сонымен бірге
үшін бұл тұжырымды дәлелдеу жеткілікті. Сонымен бірге
 ,
,
 және
және
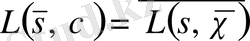 функцияларының сипаты болып табылады.
функцияларының сипаты болып табылады.
Айталық,
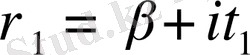 -
-
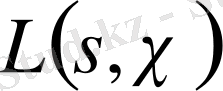 функциясының нөлі болсын, сонымен қатар
функциясының нөлі болсын, сонымен қатар
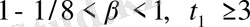 . Егер біз
. Егер біз
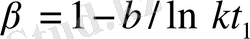 деп жорамалдасақ, онда
деп жорамалдасақ, онда
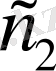 қолайлы болғанда
қолайлы болғанда
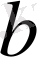
 екенін көрсету жеткілікті. Ол
екенін көрсету жеткілікті. Ол
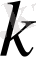 және
және
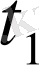 ден тәуелсіз.
ден тәуелсіз.
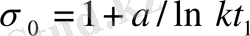 деп жорамалдаймыз. Мұнда, айталық,
деп жорамалдаймыз. Мұнда, айталық,
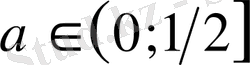 және жағдайға байланысты тағы кішіреуі қажет.
және жағдайға байланысты тағы кішіреуі қажет.
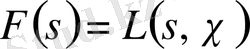 ,
,
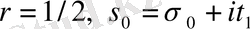 үшін төмендегі теореманы қолданамыз.
үшін төмендегі теореманы қолданамыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz