Экономикалық процестерді зерттеудегі сызықтық бағдарламалау модельдері және шешу әдістері


КУРСТЫҚ ЖҰМЫС
ЭКОНОМИКАЛЫҚ ПРОЦЕСТЕРДІ ЗЕРТТЕУДЕГІ СЫЗЫҚТЫҚ БАҒДАРЛАМАЛАУ МОДЕЛЬДЕРІ
МАЗМҰНЫ
КІРІСПЕ . . . . 3
І БӨЛІМ. ТЕОРИЯЛЫҚ БӨЛІМ . . . 4
- Жоспарлау мен басқарудағы оптималдылық қағидасы және оптималды бағдарламалаудың жалпы есебі . . . 4
- Сызықтық бағдарламалау есебі және оның шешімдерінің қасиеттері……… . . . 8
- Сызықтық бағдарламалау есебін графиктік әдіспен шешу . . . 9
- Сызықтық бағдарламалау есебін шешудің симплекстік әдісі . . . 10Қарапайым базисті симплекс әдісі . . . 10Жасанды базисті симплекс әдісі (М-есебі) . . . 14
- Сызықтық бағдарламалаудың екі жақты есептері . . . 16
ІІ БӨЛІМ. ПРАКТИКАЛЫҚ БӨЛІМ . . . 19
ҚОРЫТЫНДЫ . . . 25
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . 26
КІРІСПЕ
Өзінің мүмкіндіктерін тиімді пайдалану арқылы жоғары нәтижеге жету кез келген адамның негізгі мақсаттарының бірі. Экономикалық жүйелердің әр түрлі деңгейлерінде кездесетін жоспарлау, басқару, шектелген ресурстарды тиімді бөлу, өндірістік процестерді талдау, күрделі объектілерді жобалау сияқты есептердің ұтымды және оптималды шешімдерін табу табиғи және ғылыми-техникалық прогресс қажеттіліктерінен туған мәселелер.
Оптимизациялық есептерде математикалық әдістерді пайдалану үшін, ең алдымен, тиімді шешімін табу қажет есептің өзінің математикалық қойылымын жазуымыз қажет. Математикалық қойылымда берілген ресурстар, өндірістік технология, «жақсы» немесе «жаман» шешім деген сияқты түсініктердің сан шамалары және олардың арасындағы байланыстар, математикалық өректер, теңсіздіктер арқылы көрсетілулері тиіс. Шарттары нақты берілген есептің математика тіліндегі формалды жазылымын сол есептің математикалық моделі деп атайды.
Математикалық модель құру үшін, ең алдымен, зерттейтін объектінің ең басты қасиеттерін немесе заңдылықтарын бөліп алып, оларды математикалық өрнектер арқылы өзара байланыстырып сипаттайды. Математикалық модель құрғаннан кейін ғана есепті шешіп, зерттеу үшін математикалық әдістерді қолдануға болады.
Экономикалық процестердің математикалық модельдерін құрастыру өте күрделі мәселе, себебі ол үшін математикалық және экономикалық білгірлікті өзара ұштастыра білу қажет.
Оптимизациялау теориясында мүмкін болатын шешімдердің ішінен мақсат функциясы деп аталатын функцияға ең үлкен немесе ең кіші мән беретін «ең жақсы» шешімді табу әдістерін зерттеу мәселелері қарастырылады. Мысалы, кез келген өндіріс фирмасының негізгі мақсаты - көбірек пайда табу.
Осындай есептердің қойылымы мен шығару әдістері мақсат функциясының қасиеттері мен шешімдер жиыны жөніндегі информация көлеміне байланысты.
Мақсат функциясы мен мүмкін шешімдер жиынын сипаттайтын функциялар сызықты функциялар түрінде берілген есептер экономикалық тәжірибеде жиірек кездеседі.
Бұл курстық жұмыста сызықтық бағдарламалау есептерінің қойылымдарының математикалық модельдері және оларды шығару жолдары қарастырылған. Есептердің шығарылу әдістері экономикалық және математикалық тұрғыдан талданып келтірілген.
І БӨЛІМ. ТЕОРИЯЛЫҚ БӨЛІМ
- Жоспарлау мен басқарудағы оптималдылық қағидасы және оптималды бағдарламалаудың жалпы есебі
Сызықтық бағдарламалау оптималды бағдарламалаудың бір бөлімі болып табылады. Ал оптималды бағдарламалау өз кезегінде шартты оптимизация есептерін оқытатын қолданбалы математиканың бір бөлімі. Экономикада мұндай есептер жоспарлау мен басқарудағы оптималдылық қағидасынының практикада қолданылу кезінде туындайды. [1]
Жоспарлау мен басқаруда оптималдылық қағидасын қолданудың маңызды шарты болып жоспарлы басқару шешімін қабылдауға қажетті икемділік пен өндірістік шаруашылық жағдайындағы баламалылық (альтернативтілік) табылады. Тап дәл осындай жағдайлар, негізінен, шаруашылық жүргізуші субъектілердің күнделікті тәжірибесін (практикасын) құрайды (өндірістік бағдарламаларды таңдау, жабдықтаушылармен қатынас, маршруттарды анықтау, материалдар жинау, қоспалар дайындау және т. с. с. ) .
Оптималдылық қағидасының мәні - шаруашылық жүргізуші субъектінің өндірістік қызметінің ішкі мүмкіндіктері мен сыртқы жағдайларын ең жақсы жолмен айқындайтын
X = (x
1
, x
2
, …, x
n
)
жоспарлы басқару шешімін таңдауға ұмтылуда, мұнда
x
j
, j =
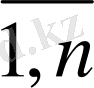 - оның компоненттері.
- оның компоненттері.
Мұндағы «ең жақсы жолмен» сөздері оптималдылықтың қандай да бір критерийін таңдауды, яғни әр түрлі жоспарлы басқару шешімдерінің ішінен салыстыру арқылы ең тиімдісін таңдауға мүмкіндік беретін экономикалық көрсеткішті білдіреді.
«Өндірістік қызметтің ішкі мүмкіндіктері мен сыртқы жағдайларын айқындайтын» сөздері жоспарлы басқару шешімдерін таңдауда бірқатар шарттардың қойылуын білдіреді, яғни X таңдау қандай да бір D мүмкін болатын шешімдер облысында жүзеге асырылады; бұл облысты, басқаша, есептердің анықталу облысы деп те атайды.
Сонымен, жоспарлау мен басқаруда оптималдылық қағидасының тәжірибеде қолданылуы дегеніміз мынадай экстремалды есеп түрін шешу:
X ∊ D, (1. 2)
f (X) → max (min), (1. 1)
мұнда f (X) - оптималды критерийдің математималық түрде жазылуы - мақсат функциясы. Әдетте шартты оптимизация есебі былай жазылады:
Мына шектемелерді (шарттарды) қанағаттандыратын:
φ 1 (x 1 , x 2 , …, x n ) {≤, =, ≥} b 1 ,
φ 1 (x 1 , x 2 , …, x n ) {≤, =, ≥} b 2 ,
(1. 4)
φ m (x 1 , x 2 , …, x n ) {≤, =, ≥} b m ,
x
j
≥ 0, j =
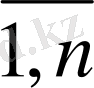 , (1. 5)
, (1. 5)
және
f (X) = f (x 1 , x 2 , …, x n ) → max (min) (1. 3)
функциясының максимум немесе минимум мәнін табу.
(1. 5) шарты міндетті емес, бірақ оған қажетті жағдайда жетуге болады. {≤, =, ≥} белгілінуі белгілі бір шектемеде ≤, = немесе ≥ таңбаларының біреуін қолдануға болатындығын білдіреді. Егер қысқаша түрде жазатын болсақ төмендегідей болады:
φ
i
(x
1
, x
2
, …, x
n
) {≤, =, ≥} b
i
, i =
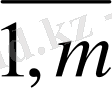 , (1. 7)
, (1. 7)
x
j
≥ 0, j =
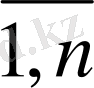 , (1. 8)
, (1. 8)
f (x 1 , x 2 , …, x n ) → max (min) (1. 6)
(1. 6) - (1. 8) есеп - оптималды (математикалық) бағдарламалаудың жалпы есебі, немесе негізінде оптималдылық және жүйелілік қағидасы жатқан оптималды бағдарламалау есебінің математикалық моделі.
X
векторы (басқарушы айнымалылар жиынтығы
x
j
, j =
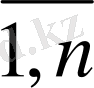 ) мүмкін болатын шешім немесе оптималды бағдарламалау есебінің жоспары деп аталады, егер де ол шектемелер жүйесін қанағаттандырса.
f (x
1
, x
2
, …, x
n
)
мақсат функциясының максимум немесе минимум мәнін беретін сол
X
жоспары оптималды бағдарламалаудың оптималды жоспары деп аталады.
) мүмкін болатын шешім немесе оптималды бағдарламалау есебінің жоспары деп аталады, егер де ол шектемелер жүйесін қанағаттандырса.
f (x
1
, x
2
, …, x
n
)
мақсат функциясының максимум немесе минимум мәнін беретін сол
X
жоспары оптималды бағдарламалаудың оптималды жоспары деп аталады.
Сонымен, белгілі бір өндірістік жағдайдағы оптималды жоспар таңдау экономикалық-математикалық модельдің жүйелілік және оптималдылық тұрғысымен және оптималды бағдарламалау есебін шешумен байланысты.
Оптималды бағдарламалау есебін жалпы түрде мынадай белгілері бойынша жіктеуге болады:
- Айнымалылардың өзара байланысу мінездемесі бойынша:
а) сызықтық;
ә) сызықтық емес.
а) жағдайында шектемелер жүйесіндегі барлық функционалдық байланыстар мен мақсат функциясы - сызықтық функциялар; жоғарыда аталғандардың біреуінде сызықтық еместіктің болуы ә) жағдайына алып келеді.
- Айнымалылардың өзгеру мінездемесібойынша:
а) үздіксіз;
ә) дискретті.
а) жағдайында басқарушы айнымалылар мәндері қандай да бір нақты сандар облысын толтыруы мүмкін; ә) жағдайында барлық айнымалылар немесе тек бір ғана айнымалы бүтін мән қабылдауы мүмкін.
- Уақыт факторын ескеру арқылы:
а) статикалық;
ә) динамикалық.
а) есептерінде модельдеу мен шешім қабылдау модель элементтерінің уақыт кезеңінен тәуелсіз болжамы негізінде жоспарлы басқару шешімі қабылданады; ә) жағдайында мұндай болжам жеткілікті анықталып қабылдана алмайды, сондықтан уақыт факторын ескеру қажет.
- Айнымалылар туралы ақпараттар бойынша:
а) толық анықталғандық (детерминделгендік) жағдайындағы есептер;
ә) ақпараттың жеткіліксіз жағдайындағы есептер;
б) анықталмағандық жағдайындағы есептер.
ә) есептерінде жеке элементтері ықтималды мүмкін шамалар болып табылады, бірақ белгілі немесе қосымша статистикалық зерттеулер арқылы олардың үлестірім заңдылықтары бекітілуі мүмкін. Ал б) жағдайында кездейсоқ элементтердің мүмкін нәтижелері туралы болжамжасауға болады, бірақ бұл нәтижелердің ықтималдықтары туралы шешім шығаруға мүмкіндік жоқ.
- Баламаларды бағалау критерийлерінің саны бойынша:
а) жай, бір критерийлі есептер;
ә) күрделі, бірнеше критерийлі есептер.
а) есептерін экономикалық тұрғыдан қарастырсақ, бір критерийлі оптималдылықтарды пайдаланған жөн немесе арнайы процедуралар (мысалы, басымдылықтарды өлшеу (салыстыру) ) арқылы көп критерийлі ізденісті бір критерийліге келтірген дұрыс.
1 - 5 белгілерінің жиынтығы оптималды бағдарламалау есептері мен әдістерін жалпы түрде топтастыруға мүмкіндік береді, мысалы: 1а) 2а) 3а) 4а) 5а) - сызықтық бағдарламалаудың есептері мен әдістері, 1ә) 2а) 3а) 4а) 5а) - сызықтық емес бағдарламалаудың есептері мен әдістері, 1а) 2ә) 3а) 4а) 5а) - бүтінмәнді (дискретті) сызықтық бағдарламалаудың есептері мен әдістері және т. б.
- Сызықтық бағдарламалау есебі және оның шешімдерінің қасиеттері
Берілген ресурстарды (қорларды) тиімді пайдалану арқылы қосымша пайданы арттыру немесе өндірістегі жалпы шығынды төмендету сияқты экономикалық есептердің математикалық модельдері сызықтық бағдарламалау есебі түрінде былайша қойылады:
Мына шектемелерді қанағаттандыратын:
a 11 x 1 + a 12 x 2 + … + a 1n x n {≤, =, ≥} b 1 ,
a 21 x 1 + a 22 x 2 + … + a 2n x n {≤, =, ≥} b 2 ,
(2. 2)
a m1 x 1 + a m2 x 2 + … + a mn x n {≤, =, ≥} b m ,
x
j
≥ 0, j =
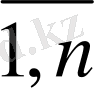 (2. 3)
(2. 3)
және
f (x) = c 1 x 1 + c 1 x 1 + … + c 1 x 1 → max (min) (2. 1)
мақсат функциясына максимум (немесе минимум) мәнін беретін n компонентті x = (x 1 , x 2 , …, x n ) векторын табу.
Мұндағы a ij , b i , c j - берілген тұрақты сандар, ал m < n; b i - оң сандар.
Экономикалық есептердің қойылу ерекшеліктеріне және математикалық зерттеулердің ыңғайына қарай сызықтық бағдарламалау есебі өзара пара-пар бірнеше түрде қойылады:
Мынадай түрде жазылған қойылымдар практикада жиірек кездеседі:
Матрицалық қойылым:
Мына шектемелерді қанағаттандыратын:
AX = B,
x ≥ 0
және
f (x) → max (min)
мәнін беретін x = (x 1 , x 2 , …, x n ) векторын табу.
Мұндағы A = (a ij ) m x n - m жатық (көлбеу) жолдан және n тік жолдан тұратын матрица.
B = (b 1 , b 2 , …, b m ) - m - компонентті тік вектор,
C = (c 1 , c 2 , …, c n ) - n - компонентті жатық вектор.
Векторлық қойылым:
Мына шектемелерді қанағаттандыратын:
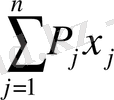 = b
= b
x j ≥ 0, j = 1, 2, …, n
және
f (x) =
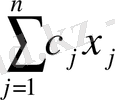 → max (min)
→ max (min)
мәнін беретін x = (x 1 , x 2 , …, x n ) векторын табу.
Мұндағы
P
j
=
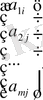 -
A
матрицасының
j
-ші тік жолының элементтерінен құралған вектор.
-
A
матрицасының
j
-ші тік жолының элементтерінен құралған вектор.
Енді сызықтық бағдарламалау есебінің қасиеттерін тұжырымдауға қажетті бірнеше анықтамаларды қарастырайық. [2] .
Бірінші анықтама. (2. 2) және (2. 3) шектемелерді қанағаттандыратын n компонентті x = (x 1 , x 2 , …, x n ) векторы сызықтық бағдарламалау есебінің жоспары деп аталады.
Екінші анықтама. Егер мына жіктемедегі
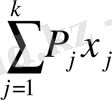
P 1 , P 2 , …, P k - векторлары сызықты тәуелсіз болып және x i =1, 2, …, k сызықтық коэффициенттері оң болатын болса, онда осы коэффициенттерден құралған x = (x 1 , x 2 , …, x n ) векторы тіректі жоспар деп аталады.
m компонентті векторлардан құралған сызықты тәуелсіз векторлардың саны әруақытта m -нен аспайтындықтан, кез келген тіректі жоспардың нөлден үлкен компоненттерінің саны да m -нен артық бола алмайды, k ≤ m .
Үшінші анықтама. Оң компоненттерінің саны m -ге тең болатын тіректі жоспар ерекше емес тіректі жоспар деп аталады.
Төртінші анықтама. (2. 1) - (2. 3) сызықтық бағдарламалау есебінің (2. 1) мақсат функциясына максимум (минимум) мәнін беретін жоспар оның оптималдық жоспары немесе шешімі деп аталады.
Енді осы анықтамалар негізінде сызықтық бағдарламалау есебінің шешімдер жиынының қасиеттерімен танысамыз:
- Сызықтық бағдарламалау есебінің жоспарлар жиыны әруақытта да дөңес көпбұрыш болады.
- Сызықтық бағдарламалау есебінің оптималдық жоспары мүмкіндік шешімдер жиынының шеткі нүктелерінің ішінен табылады. Егер шеткі нүктелерінің бірнешеуі бірдей оптималдық жоспар болатын болса, онда осы нүктелердің кез келген дөңес комбинациясы да сызықтық бағдарламалау есебінің оптималдық жоспары болады.
- ЕгерP1, P2, …, Pkвекторлар жүйесі сызықты тәуелсіз болып және мына векторлық теңдік орындалса:
P 1 x 1 + P 2 x 2 + …+ P k x k = b
x j ≥ 0, i =1, 2, …, k,
онда x = (x 1 , x 2 , …, x k , 0, 0, …, 0 ) - n компонентті векторы S мүмкін шешімдер жиынының шеткі нүктесі болады.
Керісінше, егер x = (x 1 , x 2 , …, x n ) векторы S мүмкіндіктер жиынының шеткі нүктесі болса, онда оның оң компоненттеріне сәйкес келетін P i векторлары сызықты тәуелсіз жүйе құрайды.
Осыдан x = (x 1 , x 2 , …, x n ) нүктесінің S дөңес көпбұрышының шеткі нүктесі болатындығын немесе болмайтындығын P i , i = 1, 2, …, n векторлары арқылы анықтауға мүмкіндік береді.
m компонентті P 1 , P 2 , …, P n векторларынан құралған кез келген m + 1 векторлар әруақытта сызықты тәуелді жүйе болатындықтан, S дөңес көпбұрышының кез келген шеткі нүктесіне m вектордан тұратын сызықты тәуелсіз жүйе сәйкес келеді.
Сонымен, кез келген x = (x 1 , x 2 , …, x n ) ∊ S шеткі нүктесіне P 1 , P 2 , …, P m сызықты тәуелсіз векторлар жүйесі сәйкес келеді де, мына шарттар орындалады:
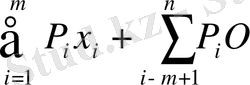 = b
= b
x j ≥ 0, i =1, 2, …, m.
- Сызықтық бағдарламалау есебін графиктік әдіспен шешу
Егер сызықтық бағдарламалау есебі екі айнымалылы шектемелермен берілетін болса, онда оны графиктік әдіспен шешуге болады:
Мына шектемелерді қанағаттандыратын:
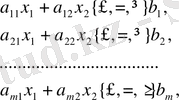 (3. 2)
(3. 2)
 (3. 3)
(3. 3)
және
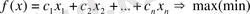 (3. 1)
(3. 1)
мақсат функциясына максимум (немесе минимум) мәнін беретін
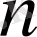 компонентті
компонентті
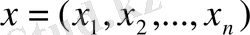 векторын табу. [1] .
векторын табу. [1] .
Сызықтық бағдарламалау есебін графиктік әдіспен шешу келесі қадамдардан тұрады:
Бірінші қадам.
Ең алдымен
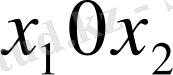 координаттар жазықтығында шектемелерге сәйкес мүмкін болатын дөңес жиын (мүмкін шешімдер облысы, анықталу облысы) тұрғызылады. Содан кейін
координаттар жазықтығында шектемелерге сәйкес мүмкін болатын дөңес жиын (мүмкін шешімдер облысы, анықталу облысы) тұрғызылады. Содан кейін
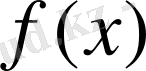 мақсат функциясының мүмкін шешімдер облысында жататын қандай да бір
мақсат функциясының мүмкін шешімдер облысында жататын қандай да бір
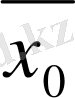 нүктесінде жататын вектор-градиент салынады:
нүктесінде жататын вектор-градиент салынады:
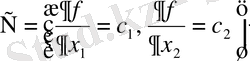 .
.
Екінші қадам.
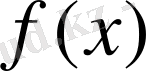 максимумға ұмтылған жағдайда вектор-градиентке перпендикуляр
максимумға ұмтылған жағдайда вектор-градиентке перпендикуляр
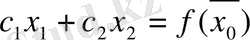 түзуі дөңес жиынның шеткі нүктесіне жеткенге дейін осы вектор бағытында қозғалады. Бұл қозғалыстағы жиынның шеткі нүктесі (немесе шеткі нүктелері)
түзуі дөңес жиынның шеткі нүктесіне жеткенге дейін осы вектор бағытында қозғалады. Бұл қозғалыстағы жиынның шеткі нүктесі (немесе шеткі нүктелері)
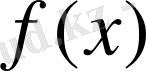 функциясының максимум нүктесі болып табылады.
функциясының максимум нүктесі болып табылады.
Үшінші қадам.
Максимум нүктесінің координаттарын табу үшін өзара максимум нүктесінде қиылысатын түзулердің теңдеулер жүйесін шешу жеткілікті. Алынған нүктедегі
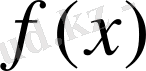 функциясының мәні максимум болып табылады.
функциясының мәні максимум болып табылады.
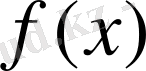 функциясын минимумдау жағдайында
функциясын минимумдау жағдайында
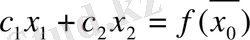 түзуін вектор-градиентке қарама-қарсы бағытта жылжыту қажет. Түсінікті, егер түзу қозғалыс кезінде мүмкін шешімдер облысынан шыға алмаса, онда сәйкес
түзуін вектор-градиентке қарама-қарсы бағытта жылжыту қажет. Түсінікті, егер түзу қозғалыс кезінде мүмкін шешімдер облысынан шыға алмаса, онда сәйкес
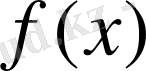 максимум немесе минимум жоқ.
максимум немесе минимум жоқ.
- Сызықтық бағдарламалау есебін шешудің симплекс әдісі
Есеп векторлық түрде қойылған болсын:
Мына шектемелерді қанағаттандыратын:
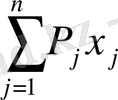 (4. 2)
(4. 2)
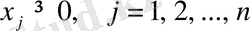 (4. 3)
(4. 3)
және
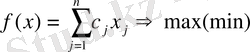 (4. 1)
(4. 1)
мақсат функциясына максимум (минимум) мәнін беретін
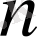 компонентті
компонентті
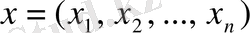 векторын табу керек.
векторын табу керек.
(4. 1) - (4. 3) түрінде қойылған сызықтық бағдарламалау есебінің мүмкін шешімдер жиынының бір шеткі нүктесінен екінші шеткі нүктесіне ауысуға болатындығын өткен бөлімде қарастырған болатынбыз.
Осылайша көшу барысында мақсат функциясының мәні біртіндеп өсіп отыратын болса, онда шеткі нүктелер арқылы нысаналы жылжу процесін бірнеше рет қайталанғаннан кейін оптималдық шешім табылады.
Осы есептеу процесін іске асыру барысында кезекті қадамда табылған шеткі нүктені екі көрсеткіші бойынша тексеруге тура келеді:
Бірінші, мақсат функциясының жаңадан табылған шеткі нүктедегі мәні өткен жолы табылған нүктедегі мәнінен артық болатындығын қамтамасыз ету.
Екіншіден, жаңадан табылған шеткі нүктенің оптималдық шешім еместігін аналитикалық сипаттамалар арқылы тексере отырып есептеу процесін тоқтату немесе одан әрі жалғастыру. Енді осы қойылған сұрақтар талаптарына орай қолданылатын математикалық әдістердің теориялық негіздерін келтіреміз.
- Қарапайым базисті симплекс әдісі
Есеп векторлық түрде қойылған болсын:
Мына шектемелерді қанағаттандыратын:
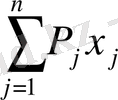 (4. 2. 2)
(4. 2. 2)
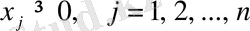 (4. 2. 3)
(4. 2. 3)
және
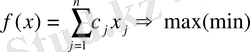 (4. 2. 1)
(4. 2. 1)
мақсат функциясына максимум (минимум) мәнін беретін
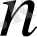 компонентті
компонентті
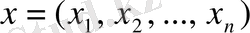 векторын табу. [4] .
векторын табу. [4] .
Мұндағы
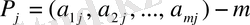 - компонентті тік жолдық вектор
- компонентті тік жолдық вектор
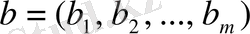 .
.
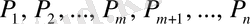 - векторларынан құралған кез келген
- векторларынан құралған кез келген
 вектор сызықты тәуелсіз тәуелсіз жүйе құрайды және олардың ішінде бірлік векторлардан құралған бірлік базис бар делік. Егер бірлік базис алғашқы орналасқан векторлардан тұрады десек, онда мынадай квадрат матрица шығады:
вектор сызықты тәуелсіз тәуелсіз жүйе құрайды және олардың ішінде бірлік векторлардан құралған бірлік базис бар делік. Егер бірлік базис алғашқы орналасқан векторлардан тұрады десек, онда мынадай квадрат матрица шығады:
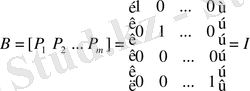
Бірлік матрицаға сәйкес келетін
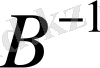 кері матрицасында
кері матрицасында
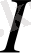 бірлік матрица болатындығына сүйене отырып, алғашқы тіректі жоспарды былайша өрнектей аламыз:
бірлік матрица болатындығына сүйене отырып, алғашқы тіректі жоспарды былайша өрнектей аламыз:
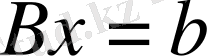
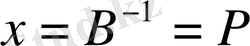 (4. 2. 4)
(4. 2. 4)
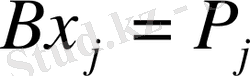
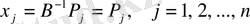 (4. 2. 5)
(4. 2. 5)
мұрдағы
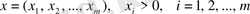
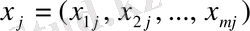
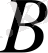 базисі
базисі
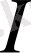 бірлік матрицасы болғандықтан, (4. 2. 5) теңдіктер бойынша
бірлік матрицасы болғандықтан, (4. 2. 5) теңдіктер бойынша
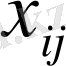 жіктелу коэффициенттері
жіктелу коэффициенттері
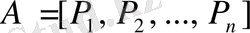 матрицасының сәйкес
матрицасының сәйкес
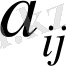 элементтеріне тең болады:
элементтеріне тең болады:
 .
.
Сонда
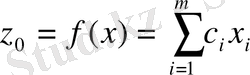 (4. 2. 6)
(4. 2. 6)
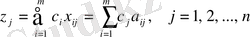 (4. 2. 7)
(4. 2. 7)
Енді
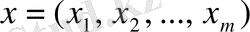 тіректі шешімінің оптималдығын тексеруге және келесі оптималдық шешімге ауысуға қажетті (4. 2. 4) - (4. 2. 7) өрнектерінен алынған барлық деректерді (есеп шығару процесінде көрнектірек болу үшін)
тіректі шешімінің оптималдығын тексеруге және келесі оптималдық шешімге ауысуға қажетті (4. 2. 4) - (4. 2. 7) өрнектерінен алынған барлық деректерді (есеп шығару процесінде көрнектірек болу үшін)
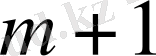 жатық жолынан және
жатық жолынан және
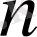 тік жолынан тұратын симплекс кестесіне орналастырамыз (1-кесте) .
тік жолынан тұратын симплекс кестесіне орналастырамыз (1-кесте) .
Симплекс кестесі
1-кесте. Есептеу процесінің алғашқы қадамы (итерациясы) .
Тіректі шешімнің базистік (оң) компоненттері
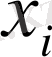 , мақсат функциясының оларға сәйкес келетін компоненттері
, мақсат функциясының оларға сәйкес келетін компоненттері
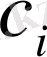 және әрбір
және әрбір
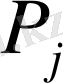 тік жолының
тік жолының
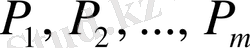 базисіне сәйкес келетін
базисіне сәйкес келетін
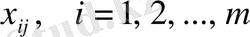 жіктелу коэффициенттері симплекс кестесінің алғашқы
жіктелу коэффициенттері симплекс кестесінің алғашқы
 жолдарының торларына жазылады.
жолдарының торларына жазылады.
Ал кестенің соңғы
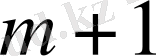 -ші жолының торларына мақсат функциясының тіректі шешіміндегі мәні
-ші жолының торларына мақсат функциясының тіректі шешіміндегі мәні
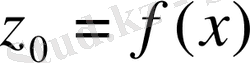 және
және
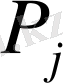 тік жолдарының базис бойынша есептелген
тік жолдарының базис бойынша есептелген
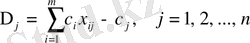 бағалары жазылады.
бағалары жазылады.
Осы
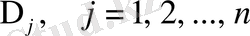 бағаларының ішінде ең болмағанда біреуінің мәні теріс болсын делік. Онда оптималдық емес белгісі туралы теорема бойынша табылған
бағаларының ішінде ең болмағанда біреуінің мәні теріс болсын делік. Онда оптималдық емес белгісі туралы теорема бойынша табылған
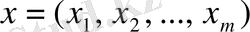 векторы оптималдық шешім бола алмайды, яғни
векторы оптималдық шешім бола алмайды, яғни
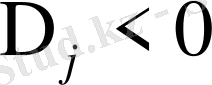 теңсіздігі мүмкін шешімдер жиынында «жақсырақ» шешімдер бар екендігін көрсетеді. «Жақсырақ» шешімнің біреуін табу үшін теріс бағалы
теңсіздігі мүмкін шешімдер жиынында «жақсырақ» шешімдер бар екендігін көрсетеді. «Жақсырақ» шешімнің біреуін табу үшін теріс бағалы
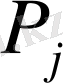 тік жолдарының біреуін базиске енгіземіз. Ол тік жолдың нөмірі мына формула бойынша анықталады:
тік жолдарының біреуін базиске енгіземіз. Ол тік жолдың нөмірі мына формула бойынша анықталады:
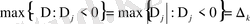 ,
,
яғни
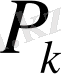 векторын базиске енгізу арқылы жақсартылған шешімді таба аламыз.
векторын базиске енгізу арқылы жақсартылған шешімді таба аламыз.
Ескі базистен шығарылатын вектордың нөмірі мына өрнек бойынша анықталады:
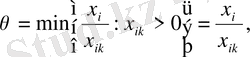
яғни
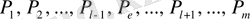 базистік векторларының ішінен
базистік векторларының ішінен
 векторы шығарылады да, оның орнына
векторы шығарылады да, оның орнына
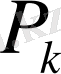 жаңа векторы енеді. Сонда жаңа табылған шешім
жаңа векторы енеді. Сонда жаңа табылған шешім
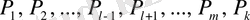 векторларынан тұратын базис бойынша сипатталады.
векторларынан тұратын базис бойынша сипатталады.
Симплекс кестесінің келесі итерациядағы элементтері есептеу геометриялық тұрғыдан мынадай тік төртбұрыш схемасына сәйкес келеді:
1.
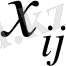

-
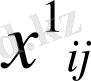 жіктелу коэффициенттерін
жіктелу коэффициенттерін
есептеу үшін.
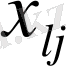
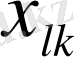
2.
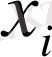
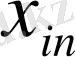
-
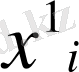 жаңа базистік компоненттерін
жаңа базистік компоненттерін
есептеу үшін.
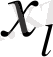
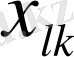
3.
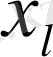
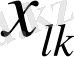
- Мақсат функциясының жаңа тіректі
жоспардағы
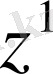 мәнін есептеу үшін.
мәнін есептеу үшін.

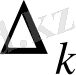
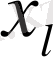
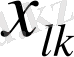
-
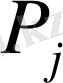 тік жолдарының жаңа базиске
тік жолдарының жаңа базиске
сәйкес келетін
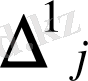 бағаларын есептеу
бағаларын есептеу

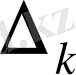 үшін.
үшін.
(4. 2. 12) - (4. 2. 14) формулаларының есептеу схемалары матрицаның
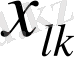 бас элементін таңдап алып Жордан-Гаусстың белгісіз айнымалыларды біртіндеп шығару арқылы матрицаны түрлендіру схемасына негізделген.
бас элементін таңдап алып Жордан-Гаусстың белгісіз айнымалыларды біртіндеп шығару арқылы матрицаны түрлендіру схемасына негізделген.
Сонымен, белгілі бір итерацияға сәйкес симплекс кестесінің барлық элеметтері анықталған болса, онда симплекс кестесінің келесі итерацияға сәйкес келетін элементтері мына ретпен анықталады:
- Симплекс кестесінің-ші жолында жазылғанбағаларының таңбалары бойынша табылған тіректі жоспардың оптималдылығын тексереміз. Егер барлықтік жолдар үшінболса, онда табылған тіректі жоспар оптималды болады.
- Егер-дің белгілі мәндеріндетеріс бағалар сәйкес келетін болса, онда табылған тіректі жоспар оптималды болмайды да, одан «жақсырақ» тіректі жоспарды табу үшінөрнегі бойынша анықталғантік жолы базиске енгізіледі.
- өрнегі бойынша анықталғанвекторы ескі базистен шығарылып қалады. Егермәндерінің барлығынатеріс мәндер сәйкес келетін болса, онда мақсат функциясының максимум мәні шексіздік болады.
- Базиске енгізілетінтік жолы мен базистен шығарылатынжолы анықталғаннан кейінбас элементі бойынша симплекс кестесінің элементтері (4. 2. 12) - (4. 2. 14) рекуренттік формулаларының көмегімен түрлендіріледі.
Соның нәтижесінде жаңа тіректі жоспар және оған сәйкес келетін базис бойынша есептелген жіктелу коэффициенттері,
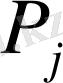 тік жолдарының бағалары және мақсат функциясының мәні анықтлады.
тік жолдарының бағалары және мақсат функциясының мәні анықтлады.
1 - 4 кезеңдерде көрсетілген түрлендірулер арқылы тіректі шешімдер біртіндеп «жақсартыла» береді де, бірнеше итерациядан оптималдық белгісін қанағаттандыратын (яғни
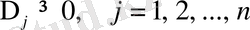 болатын) оптималды тіректі шешім табылады.
болатын) оптималды тіректі шешім табылады.
2-кесте. Есептеу процесінің екінші итерациясы.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz