Ляпуновтың бірінші әдісі және автоматты реттеу жүйелерінің орнықтылығын анықтау әдістері

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Ляпуновтың бірінші әдісі бойынша сызықтық емес жүйенің тұрақтылығын анықтау

Жүйенің орнықтылығы деп оның тепе-теңдік күйінен ауытқуына себеп болған әсерді алып тастағаннан кейін, бастапқы орнықтылық қалпына оралу қабілеттілігін айтады. Автоматты реттеу жүйесінің статикалық тепе-теңдік күйі әртүрлі болады. Жүйенің орнықтылық режиміндегі тепе-теңдік күйі үш түрге ажыратылады (7. 1-сурет) :

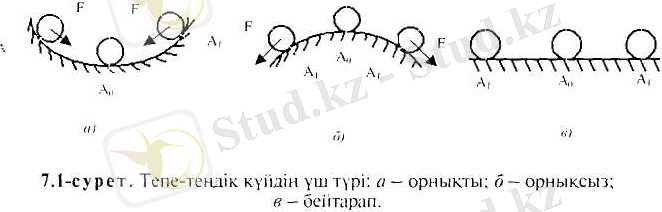
Тепе-теңдік күйдің мүмкін болатын түрлерін алдымен беттің әртүрлі нүктелерінде орналасқан шариктің «қозғалыс бағытынан қарастырайық: а) шарикті бастапқы тепе-теңдік күйіне қайтарушы Ғ күші шарик беттің қай жерінде жатса да пайда болады; б) шарик тепе-теңдік күйінен сәл ауытқыса Ғ күші пайда болып, оны одан әрі тепе-теңдік күйінен ауытқытуға тырысады; в) шарик беттің қай нүктесінде жатса да орнықты күйінде қалады.

Шарик мысалындағы тепе-теңдік түрлері жөніндегі ұғымды автоматты реттеу жүйесінде де қарастыруға болады.

Жұмыс істеп тұрған автоматты жүйеге әртүрлі тұрақты сыртқы қозулар әсер етуі салдарынан реттелетін шығыстық шаманың мәні жиі өзгеріп отырады. Жүйенің автоматты реттеуіші осы реттелетін шаманы берілген мәнге келтіруге ұмтылады. Бірақ тұтастай алғанда жүйеде инерциялық массалар, реактивті элементтер (индуктивтік, сыйымдылық) болатындықтан, оның орнықты қалпына келуі, немесе қалыптасқан бір күйден келесісіне өтуі лезде емес, белгілі түрде кешігіп жүзеге асады. Жүйеде өтпелі процесс туындайды. Бұл жағдайда, егер жүйе қозу әрекеті тоқталғаннан кейін қалыптасқан күйге оралса, ол орнықты. Егер оралмаса, онда орнықсыз. Орнықсыз жұмыс кері байланыспен қамтылған АРЖ-ның барлығында туындауы ықтимал. Қазіргі автоматты жүйелерде мынадай үш талаптар орындалуы қажет: орнықтылық шарты, өтпелі процеске және қалыптасқан режимге қойылатын талаптар АРЖ-ның орнықтылығын анықтау мәселесі басты болып саналады, өйткені орнықсыз жүйелер іс жүзінде жарамсыз.

Орнықтылықты зерттеудің жалпы әдісі АРЖ-ның g(t) жоспарлау (басқарушы) және f(t) қоздыру әсерлері тудыратын y(t) реттелетін шаманың өзгеруі үшін жазылған

(a ₀ p ⁿ +a ¹ p ^n-1 + . . . +a _n ) y(t) = (b _o p ^m +b ₁ p ^m-1 + . . . +b _m (t) (7. 1)

дифференциал теңдеуін талдаумен тұжырымдалады. g(t), f (t) мәндерін және олардың туындыларын нөлге тең деп алсақ, сипаттама теңдеуі

G(p) = a ₀ p ⁿ +a ₁ p ^n-1 + . . . +a _n =0 (7. 2)

болатын біртектес

а ₀ р ⁿ + а ₁ р ^n-1 + . . . +a _n ) у(t) =0 (7. 3)

дифференциал теңдеуін аламыз.

АРЖ-ның орнықты екендігін (7. 3) тендеуін шешу арқылы анықтауға болады. Оның шешімі өтпелі процесті сипаттайды

(7. 4)

Мұндағы С _і - интегралдау тұрақтысы, ол бастапқы шарттан анықталады;

р _і - сипаттамалық теңдеудің түбірлері. өтпелі процесс саны түбірлер санымен анықталатын құраушылар қосындысынан тұрады.

Жүйе орнықты болуы үшін (7. 4) -нің шешімі мына шартты қанағаттандыруы тиіс:

(7. 5)

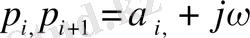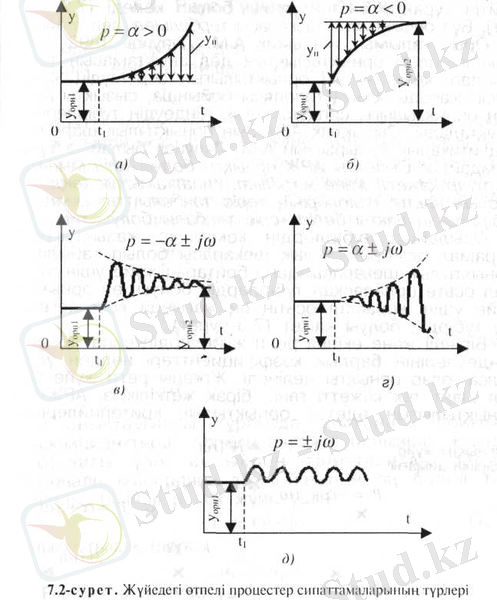
Бұл өрнек орнықтылық шартының аналитикалық өрнегі болады. Жалпы жағдайда р _і түбірлері комплекс болып келеді. Оған қоса олар түйіндес (сопряженный) түбірлердің жұбын түзеді. Егер түбірлер нақты болса (р = ±а), онда t уақыт мезетінде (7. 2, а, б-суреттер) ықпал берілгеннен кейінгі өтпелі процесстің сипаты