Дифференциалдық теңдеулерді шешудің Ранге-Кутта әдісі

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Мазмұны:

1. Кіріспе.

2. Глоссарий.

3. Негізгі бөлім.

3. 1 Дифференциалдық теңдеулерді шешудің Ранге-Кутта әдісі:түпнұсқа.

3. 2 Дифференциалдық теңдеулерді шешудің Ранге-Кутта әдісі:нәтиже.

4. Қорытынды.

5. Пайдаланған әдебиеттер.

Кіріспе

Математикада көптеген есептер теңдеу түрінде беріледі, әсіресе дифференциалдық теңдеулерді шешу қиынға соғады. Көптеген процестердің математикалық түрі, ізделінетін белгісіз шама цифр емес, ал белгілі бір аргументке тәуелді функция ретінде берілетін теңдеумен өрнектеледі. Сонымен қатар, бұл функция өз туындысы және аргументімен байланысты болады. Бұндай теңдеулер дифференциалдық теңдеулер деп аталады. Дифференциалдық теңдеулер математикалық анализ жүргізуде үлкен роль атқарады. Оның жолы басқа теңдеулерге қарағанда қиын, күрделі және де дифференциалдық теңдеулерді шешудің бірнеше жолдары бар. Сондықтан да мен «Дифференциалдық теңдеулерді шешудің Ранге-Кутта әдісі» деген тақырыпты таңдадым. Дифференциалдық теңдеулерді шешудің әдістерін жетік меңгергім келді.

Дифференциалдық теңдеулер 17 ғасырдың соңында механика, т. б. жаратылыстану пәндерінің талабына сәйкес интегралдық есептеу және дифференциалдық есептеумен қатар пайда болды. Қарапайым дифференциалдық теңдеулер Ньютонның және неміс математигі Лейбництің) еңбектерінде кездеседі. “Дифференциалдық теңдеулер” терминін ғылымға Лейбниц енгізген (1676) . Дифференциалдық теңдеулерді шешу үшін жуықтап есептеу әдістерін пайдаланғанда олардың шешімдері, яғни ізделінді функция таблицалық турде алынады. Ізделінді функцияның мәндері арнайы формулалармен есептеледі. Ранге-Кутта әдісіде дәлелденген арнайы формуласы апқылы табылады. Менің мақсатым Ранге-Кутта әдісінің, дифференциалдық теңдеулерді шешудің оңтайлы жолдарын меңгеріп, дифференциалдық теңдеулер жүесін тереңірек зертттеу, өзгелерге түсіндірін беру.

Қазіргі кезде техниканың дамуына байланысты әр түрлі химиялық, физикалық заттардың құрамын, массасын, көлемін, ұзындығын, т. б. - параметрлерін зерттеу қажеттігі туып отыр. Одан басқа бұл параметрлердің уақытқа және де т. б. шамаларға тәуелділігін де білу керек. Мұның бәрін тек дифференциалдық теңдеулер көмегімен ғана жүзеге асыруға болады.

Қазіргі уақытта дифференциалдық теңдеулер техника ғылымдарынң барлық дерлік салаларында кең қолданысқа ие болып отыр.

Глосарий

Дифференциал -(латын тіліннің «differentia» деген сөзінен шыққан айырым, ажыратылым деген мағынаны береді) айналдырушы иінді күшті жетектегі екі білік арасында берілген катынаста бөліп, олардың Әртүрлі бұрыштық жылдамдықпен айналып қозғалуын камтамасыз ететін күштік берілістің механизмі.

Параметр - (грек тілінің παραμετρέω - өлшеймін) - макродененің күйін сипаттайтын шамаларды айтады.

Функция - айнымалы шамалар арасындағы тәуелділікті білдірктін математикалық ұғым.

Интеграл -(лат. іnteger - бүтін) -өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама.

Формула - математикалық шамалардың шартты белгілермен таңбаланған қатары.

Модель -(фр. modele , лат. modulus - өлшем) - белгілі бір зерттелетін нысанның ой түсінігі арқылы немесе материалдық түрде жасалған шартты үлгісі (бейнесі, сұлбасы, сипаттамасы, т. б. ) .

Динамика -(гректің dynamikos деген сөзінен алынып, күшке тиісті, күшті деген мағынаны береді.

Дифференциалдық теңдеулерді шешудің Ранге-Кутта әдісі

Дифференциалдық теңдеулер көбінесе динамикалық модельдеу аймағын зерттегенде көп қолданылады. Олар, ереже бойынша, уақыт өтуіне байланысты параметрлердің өзгеруін қарастырады.

Дифференциалдық теңдеулер - ізделінетін функцияны оның әр түрлі ретті туындыларымен және тәуелсіз айнымалылармен байланыстыратын теңдеулер. Тәуелсіз бір айнымалыға тәуелді бір немесе бірнеше функциялардың туындылары бар дифференциалдық теңдеулерді жай дифференциалдық теңдеу деп, ал тәуелсіз бірнеше айнымалыға тәуелді функциялардың дербес туындылары бар дифференциалдық теңдеулерді дербес туындылы дифференциалдық теңдеу деп атайды. Дифференциал- дық теңдеулерге енетін туындылардың реті дифференциалдық теңдеулер дің реті делінеді.

Дифференциалдық теңдеулердің шешімдері сан емес функция болып табылады, сол себепті дифференциалдық теңдеулерді шешу қиынға түседі. Дифференциалдық теңдеулерді шешу əдістері модельдеуде жəне жеке жауап алу үшін ең маңызды болып табылады.

Дифференциалдық теңдеулерді шешудің екі класты əдісі бар: бір

қадамды жəне көп қадамды.

Бір қадамды əдіс мынадай:Yi+1= F[f(xi, yi) ], фукцияның бір ғана нүктесін тапқанда, ал екі қадамды əдіс:Yi+1 =F(yi-3, yi-2, yi-1, yi) тапқанда қолданылады. Бір қадамды əдіс класына Эйлер, $\ K_{1}^{(i) }$ Рунге-Кутта əдістері жəне

тағы басқалар жатады. Рунге-Кутта əдісін қарастырайық:

Бастапқы шарты $y\left( x_{0} \right) = y_{0}$ болатын $y' = f(x, y)$ дифференциал теңдеуін шешуге арналған Коши есебін қарастырайық. $\ \ x_{1}$ нүктесіндегі ізделінді жуық шешімді $y_{1}$ деп белгілесек. Рунге- Кутта әдісі бойынша әрбір келесі $x_{і + 1} = x_{1} + h$ нүктесіндегі $у_{і + 1}$ жуық мәнін есептеуде келксі формулалар жұбы қолданылады:

Берілген

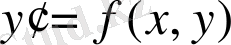(1)

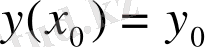(2)

есебінің 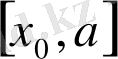аралығындағы жуық шешуінің дәлдігі -

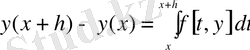(3)

Теңдігінің оң жағындағы интегралды есептеу дәлдігімен тікелей байланысты болғандықтан, осы интегралды жуықтап есептеудің Рунге-Кутта әдісін қарастырайық. Ол үшін алдымен 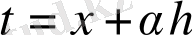айнымалысын енгізу арқылы (3) теңдігін былайша түрлендірейік:

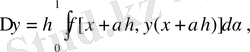(4)

мұнда 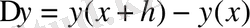. Енді

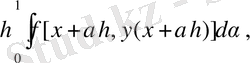(5)

интегралын есептеу үшін

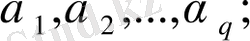
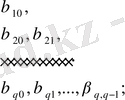
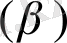
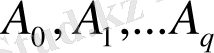(А)

параметрлерін алайықта, , 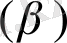параметрлерін пайдаланып

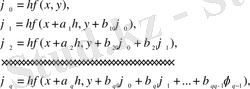
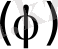
біртіндеп есептелетін тізбек құрастырып,

(6)

жуықтауы орындалатындай , , 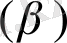(А) параметрлерін табу жолын қарастырайық.

Айталық,

(7)

болсын. 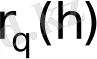жеткілікті жатық функция деп есептеп, оны былайша жіктейік:

Енді , , 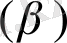(А) параметрлерін

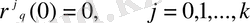(8)

болатындай етіп тапсақ, онда біздің жіберетін қатеміз:

(9)

(8) теңдігін қанағаттандыратындай , , 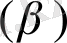(А) параметрлерін табу алгоритімі былайша іске асырылады.

Алдымен 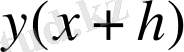- ты 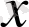нүктесінде Тэйлор қатарына жіктейміз:

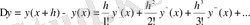. (10)

Оны -тың дәрежесі бойынша жіктелген 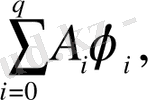өрнегімен салыстыру арқылы, белгісіздері , , 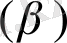(А) параметрлерінен тұратын, сызықтық емес теңдеулер жүйесін аламыз. Осы теңдеулер жүйесін шешу арқылы , , 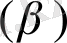(А) параметрлерін табамыз.

Кез келген үшін , , 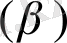(А) параметрлерін табу күрделі мәселе болғандықтан біз бұл әдістің тек дербес жағдайларын ғана қарастырамыз.

Рунге-Кутта формулалары:

$\left\{ \begin{array}{r} y_{i + 1 = y_{i} - \mathrm{\Delta}y_{i}} \\ \mathrm{\Delta}y_{i = \frac{1}{6}\left( K_{1}^{(i) } + {2K}_{2}^{(i) } \right) + 2K_{3}^{(i) }{+ K}_{4}^{(i) }} \end{array} \right. \$ $,$